「JOI Open 2020」黑白点

传送门

题意

环上有 $n$ 个黑点和 $n$ 个白点。现在要将黑点、白点通过 $n$ 条线段两两匹配，问最多几对线段相交。

$n\le 2\times 10^5$。

分析

首先，对于依次排列的 B1B2W1W2，最优方案一定不包含 B1-W2 B2-W1，因为可以调整成 B1-W1 B2-W2。

有推论：设黑、白点序列分别为 $b_1,b_2,\cdots,b_n$ 和 $w_1,w_2,\cdots,w_n$，最优方案一定是 $b$ 的某个循环移位和 $w$ 在所有下标相同的位置匹配。

聚焦于一条线段，可推得：与之不相交的线段条数为 $|l-n|$，$l$ 为线段长度。

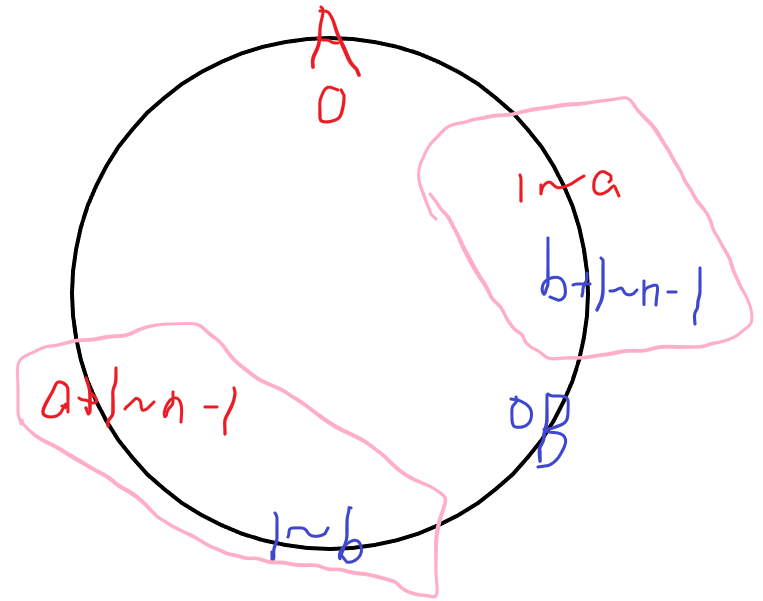
因此，把所有白点移动到正对面，问题转化为：将黑白点匹配，最小化匹配距离之和。

数轴上的问题是容易的（每段单位长度的贡献为其左侧黑点数与白点数之差的绝对值）。考虑把环复制无穷遍，相当于可以将极左侧的黑、白点数之差赋为任意整数。因此取中位数最优。

代码

提交记录

#include <bits/stdc++.h>
#define rep(i,a,b) for(int i=(a),_=(b);i<=_;++i)
#define per(i,a,b) for(int i=(a),_=(b);i>=_;--i)
#define pb push_back
#define IL inline
using namespace std;
typedef long long ll;
const int N = 4e5 + 5;
int n, m, a[N];
char s[N];
int main() {
    scanf("%d%s", &n, s + 1), m = n * 2;

    rep(i, 1, m)if (s[i] == 'B')
        ++a[i];

    rep(i, 1, m)if (s[i] == 'W')
        --a[i <= n ? i + n : i - n];

    rep(i, 1, m)a[i] += a[i - 1];
    sort(a + 1, a + m + 1);
    ll ans = ll(n) * (n - 1);
    rep(i, 1, n)ans -= a[m + 1 - i] - a[i];
    printf("%lld\n", ans >> 1);
    exit(0);
}