「CEOI2016」路由器（构造）

传送门

题意

对于常数 \(n,m,p\)，构造一个点集为 \(\{1,2,\cdots,2n+k\}\) 且边数不超过 \(m\) 的 DAG，满足：

• \(1,2,\cdots,n\) 只有出边，且 \(n+1,n+2,\cdots,2n\) 只有入边。
• \(1,2,\cdots,n\) 中每个点均可到达 \(n+1,n+2,\cdots,2n\)。
• 对于任意两点 \(x,y\)，若 \(x\) 可到达 \(y\)，则 \(x\) 到 \(y\) 的路径唯一。
• 对于任意点 \(x\)，可到达 \(x\) 的点数与 \(x\) 可到达的点数的乘积不超过 \(p\)（本题中任意点可到达自己）。

\(n=9978,m=p=10^5\)。

分析

记 \(c=\frac{n}{\sqrt p}\)。把 \([1,n]\) 和 \([n+1,2n]\) 各自均分成 \(c\) 块，然后对于两边的块建完全二分图，如下图：

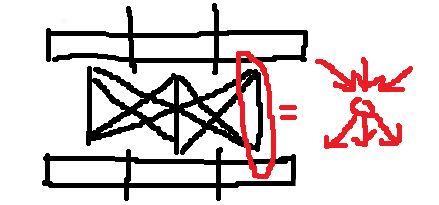
这样对图中的每个红点，可到达它的点数和它可到达的点数都是 \(\frac{n}{c}=\sqrt p\)。

但总边数 \(2nc\) 太大了。发现每个块都向 \(c\) 个红点连边，考虑优化这部分。

那么把每个块再分 \(c\) 份，然后这样构造：

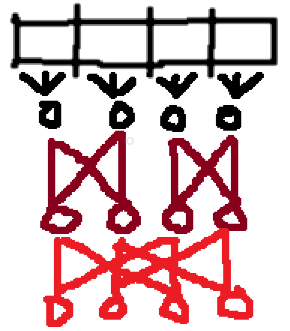
这样每往上一层，可到达 \(x\) 的点数减半，\(x\) 可到达的点数加倍，因此乘积不变。最后边数是 \(2n+4c^2\log c\)，只有 4w 多。

实现

提交记录

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=(a),_=(b);i<=_;++i)
#define per(i,a,b) for(int i=(a),_=(b);i>=_;--i)
#define pb push_back
#define IL inline
using namespace std;
typedef double db;
typedef vector<int> VI;
//head
const int narr[]={118,223,1250,5101,9934,9955,9978};
const int c=32,lim=1e5;
int n,t,id;
bool rev;
struct E{int u,v;};
vector<E> ans;
IL int sqr(int x){return x*x;}
IL void add(int u,int v){
	ans.pb(rev?E{v,u}:E{u,v});
}
void solve(VI x,VI y){
	VI z;
	for(int k=c>>1;k;k>>=1){
		swap(y,z);
		y.resize(c);
		rep(i,0,c-1)y[i]=++t;
		for(int i=0;i<c;i+=k<<1)rep(j,i,i+k-1){
			add(y[j],z[j]),add(y[j+k],z[j+k]);
			add(y[j+k],z[j]),add(y[j],z[j+k]);
		}
	}
	rep(i,0,c-1){
		for(int j=i;j<int(x.size());j+=c){
			add(x[j],y[i]);
		}
	}
}
int main(int argc,char *argv[]){
	id=atoi(argv[1]);
	n=narr[id-1];
	t=n*2;
	VI x[40],z[40],y[40],w[40];
	rep(i,1,c)for(int j=i;j<=n;j+=c){
		x[i].pb(j),z[i].pb(j+n);
	}
	rep(k,0,c-1)rep(i,1,c){
		y[i].pb(++t);
		w[(i+k-1)%c+1].pb(t);
	}
	rep(i,1,c)solve(x[i],y[i]);
	rev=1;
	rep(i,1,c)solve(z[i],w[i]);
	printf("%d %d\n",t,int(ans.size()));
	for(E e:ans){
		printf("%d %d\n",e.u,e.v);
	}
	exit(0);
}