数据挖掘-推荐算法入门
寻找相似用户
1.曼哈顿距离:计算速度快,对于Facebook这样需要计算百万用户之间的相似度时就非常有利
最简单的距离计算方式是曼哈顿距离。在二维模型中,每个人都可以用(x, y)的点来表示,这里我用下标来表示不同的人,(x1, y1)表示艾米,(x2, y2)表示那位神秘的X先生,那么他们之间的曼哈顿距离就是:
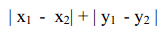
我们就可以把结果最小(距离最近)的结果最推荐给X先生。
2.欧几里得距离:
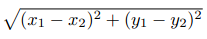
3.闵可夫斯基距离:
我们可以将曼哈顿距离和欧几里得距离归纳成一个公式,这个公式称为闵可夫斯基距离:
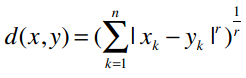
其中:
r = 1该公式即曼哈顿距离r = 2该公式即欧几里得距离r = ∞极大距离
r值越大,单个维度的差值大小会对整体距离有更大的影响。
4.皮尔逊相关系数
让我们仔细看看用户对乐队的评分,可以发现每个用户的打分标准非常不同:
- Bill没有打出极端的分数,都在2至4分之间;
- Jordyn似乎喜欢所有的乐队,打分都在4至5之间;
- Hailey是一个有趣的人,他的分数不是1就是4。
那么,如何比较这些用户呢?比如Hailey的4分相当于Jordan的4分还是5分呢?我觉得更接近5分。这样一来就会影响到推荐系统的准确性了。解决方法之一是使用皮尔逊相关系数。
皮尔逊相关系数的计算公式是:

能够计算皮尔逊相关系数的近似值:
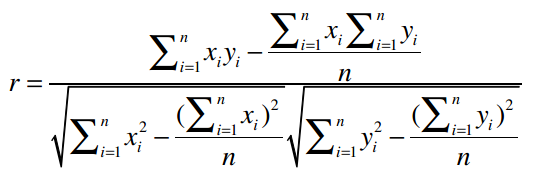
5.余弦相似度
当用户数据是稀疏的时,可以用来计算两者的相似度。余弦相似度的计算中会略过这些非零值。它的计算公式是:

余弦相似度的范围从1到-1,1表示完全匹配,-1表示完全相悖。所以0.935表示匹配度很高。
6.K最邻近算法
假设给A推荐物品b,找出K个最相似的用户,然后使用皮尔逊相关系数得到的结果,当你决定是否需要给他A推荐b时,可以计算K个最相似用户对b的评价,对其做皮尔逊相关系数加权求和。



