图神经网络

基本原理

欧几里得空间

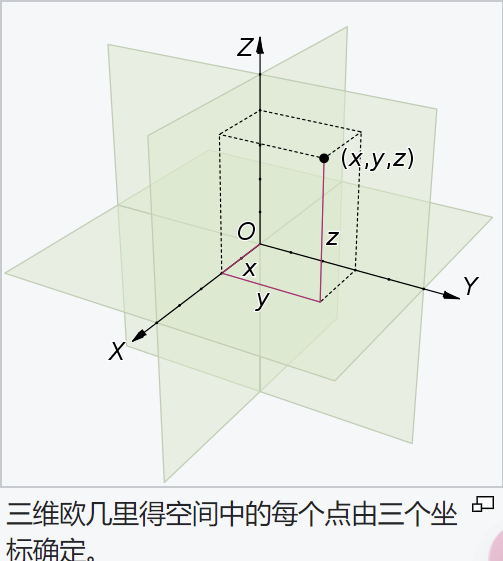
欧式空间的本质性，是其平面性.

一句话总结：欧几里得空间就是在对现实空间的规则抽象和推广（从n<=3推广到有限n维空间）。

欧几里得几何就是中学学的平面几何、立体几何，在欧几里得几何中，平行线任何位置的间距相等。

而中学学的几何空间一般是2维，3维（所以，我们讨论余弦值、点间的距离、内积都是在低纬空间总结的），如果将这些低维空间所总结的规律推广到有限的n维空间，那这些符合定义的空间则被统称为欧几里得空间（欧式空间，Euclidean Space）。

而欧几里得空间主要是定义了内积、距离、角（没错，就是初中的那些定义）。

补充：欧几里得空间中的元素可以看作点或向量。点由其坐标表示，例如在 \(\mathbb {R} ^{3}\)中，一个点 𝑃可以表示为 (𝑥,𝑦,𝑧)

为了做欧式几何，人们希望讨论两点间的距离，直线或向量间的夹角。一个自然的方法是在\(\mathbb {R} ^{n}\)上，对任意两个向量x,y,引入它们的“标准内积”<x,y>或称为点积x·y

\[ <x,y>=\sum_{i}^{n}x_{i}y_{i}=x_{1}y_{1}+x_{2}y_{2}+...+x_{n}y_{n} \]

补充：欧几里得空间可以具有任意维度，通常用符号\(\mathbb {R} ^{n}\)表示，其中
n是维度。例如，\(\mathbb {R} ^{2}\)表示二维欧几里得空间，\(\mathbb {R} ^{3}\)表示三维欧几里得空间。

也就是说，\(\mathbb {R} ^{n}\)中的任意两个向量对应着一个实数值。 我们把\(\mathbb {R} ^{n}\)及这样定义的内积，称为\(\mathbb {R} ^{n}\)上的欧几里得结构；此时的\(\mathbb {R} ^{n}\)也被称为n维欧几里得空间，内积"<,>"称为欧氏内积。

扩：内积的几何概念是两个向量的长度与它们夹角余弦的积。所以,内积又可写成

\[ x·y = |x||y|cos\theta \]

利用这个内积，可以建立距离、长度、角度等概念：

• 向量x的长度：
  \({\displaystyle \|\mathbf {x} \|={\sqrt {<\mathbf {x} ,\mathbf {x} >}}={\sqrt {\sum _{i=1}^{n}(x_{i})^{2}}}}\)
• x和y所夹的内角：
  \({\displaystyle \theta =\cos ^{-1}\left({\frac {<\mathbf {x} ,\mathbf {y} >}{\|\mathbf {x} \|\|\mathbf {y} \|}}\right)}\)
• 最后，可以利用欧式范数来定义\(\mathbb {R} ^{n}\)上的距离函数，或称度量：
  \({\displaystyle d(\mathbf {x} ,\mathbf {y} )=\|\mathbf {x} -\mathbf {y} \|={\sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}}}。\)
• 正交性：两个向量如果其内积为零，则称它们是正交的。正交向量在几何上表现为互相垂直。

GNN原理

• 图神经网络（GNN）模型原理及应用综述

•