机器学习-周志华(7-8章)
第7章 贝叶斯分类器
怎样用非数学语言讲解贝叶斯定理?---感觉像在说贝叶斯公式
带你理解朴素贝叶斯分类算法
将贝叶斯公式诠释为:在特征条件下的分类问题:\(P(类别|特征)=\frac{P(类别)P(特征|类别)}{P(特征)}\)
7.1 贝叶斯决策论

7.2 极大似然估计

7.3 朴素贝叶斯分类器


7.4 半朴素贝叶斯分类器
难点:"属性条件独立性假设"不一定成立,朴素贝叶斯的假设过于强烈
提出:半朴素贝叶斯(semi-naive Bayes)
半朴素贝叶斯:
思想:适当考虑一部分属性间的相互依赖信息。
策略:"独依赖估计"(one-dependent estimator,ODE):假设每个属性在类别之外最多仅依赖一个其他属性。即\(P(c|x)\propto P(c)\prod_{i=1}^{d}P(x_{i}|c,pa_{i}),pa_{i}为x_{i}的父属性\)
如何确定父属性?:
1、SPODE(super-parent ODE):假设所有属性都依赖同一个属性,称为“超父”。
若已知父属性,通过拉普拉斯纠正后的类条件概率\(\hat{P}(x_{i}|c)=\frac{|D_{c,x_{i}}|+1}{|D_{c}|+N_{i}}\)来估计\(P(x_{i}|c,pa_{i})\)
通过交叉验证等模型选择方法来确定父属性。
2、TAN(Tree Augmented ODE):通过最大带权生成树算法的基础上,通过以下步骤将属性间关系依赖约简为树形结构。
1、计算任意两个属性之间的条件互信息(conditional mutual information)
2、以属性为结点构建完全图,任意两个结点之间边的权重设为\(I(x_{i},x_{j}|y)\);
3、构建此完全图的最大带权生成树,挑选根变量,将边置为有向;
4、加入类别结点\(y\),增加从\(y\)到每个属性的有向边;
条件互信息刻画了属性xi和xj在已知类别情况下的相关性;通过最大生成树算法,TAN保留了强相关属性间的依赖性
3、AODE(Averaged One-dependent estimator):基于集成学习机制、更为强大的独依赖分类器。尝试将每个属性作为超父来构建SPODE,然后将有效额SPODE集成起来作为最终结果。
AODE需要估计\(P(c,x_{i})\)和\(P(x_{j}|c,x_{i})\),根据拉普拉斯修正后的式子可得:
AODE无需模型选择,既能通过预计算节省时间,也能采取懒惰学习方式,并且易于实现增量学习
独依赖不同策略的区别:


7.5 贝叶斯网
7.6 EM算法
7.7 阅读材料
第8章 集成学习
8.1 个体与集成
个体学习器:精确率仅高于的学习器。(随机判断一个二分类的精确率为,精确率高于的学习器才有意义,因为这样才有信息获取)
集成学习:又称多分类器系统(multi-classifier system)/基于委员会的学习(committee-based learning)

结构:1,基学习器:同质集成,采用同种算法的集成的个体学习器,相应算法为基学习算法;2、组件学习器:异质集成,采用不同种算法的集成的个体学习器
性能:集成学习通过将多个学习器进行结合,通常可获得比单一学习器显著优越的泛化性能。

集成原则:好而不同
分类:
- 个体学习器之间存在强依赖关系必须串行生成的序列化方法,比如Boosting
- 个体学习器之间不存在强依赖关系可同时生成的并行化方法,比如Bagging,随机森林
8.2 Boosting
Boosting思路:集成多个模型,每个模型都在尝试增强整体效果,具体来说:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值T,最终将这个T个基学习器进行加权结合。
AdaBoosting
实现:AdaBoosting-线性组合:如下图,经过第一个学习器的学习后,预测错误样本呈现深蓝色,训练正确样本呈现浅蓝色,赋予错误的训练样本更高的权重,对于经过调整的训练样本再次训练一个学习器,同理一直迭代下去。

基学习器的线性组合:\(G(x)=sign[f(x)]=sign[\alpha_{1}G_{1}(x)+\alpha_{2}G_{2}(x)+···+\alpha_{n}G_{n}(x)]\)
根据([原理推导1]),可得AdaBoosting步骤:
1、选取分类错误(e)最小的阈值,得个体学习器函数G;
2、根据分类错误e,得到系数\(\alpha\)
3、通过损失指数函数,更新权值分布,得到当前基学习器的线性输出;
4、回到步骤1,再次迭代;
原理推导:
8.3 Bagging与随机森林
Bagging是一种并行式的集成学习方法,即基学习器的训练之间没有前后顺序可以同时进行,Bagging使用“有放回”采样的方式选取训练集,对于包含m个样本的训练集,进行m次有放回的随机采样操作,从而得到m个样本的采样集,这样训练集中有接近36.8%的样本没有被采到。按照相同的方式重复进行,我们就可以采集到T个包含m个样本的数据集,从而训练出T个基学习器,最终对这T个基学习器的输出进行结合。
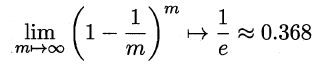
Bagging算法的流程如下所示:
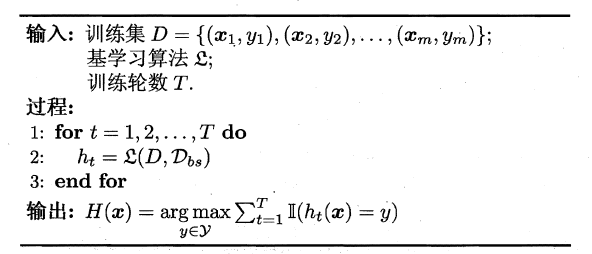
可以看出Bagging主要通过样本的扰动来增加基学习器之间的多样性,因此Bagging的基学习器应为那些对训练集十分敏感的不稳定学习算法,例如:神经网络与决策树等。从偏差-方差分解来看,Bagging算法主要关注于降低方差,即通过多次重复训练提高稳定性。不同于AdaBoost的是,Bagging可以十分简单地移植到多分类、回归等问题。总的说起来则是:AdaBoost关注于降低偏差,而Bagging关注于降低方差。
随机森林(Random Forest)是Bagging的一个拓展体,它的基学习器固定为决策树,多棵树也就组成了森林,而“随机”则在于选择划分属性的随机,随机森林在训练基学习器时,也采用有放回采样的方式添加样本扰动,同时它还引入了一种属性扰动,即在基决策树的训练过程中,在选择划分属性时,RF先从候选属性集中随机挑选出一个包含K个属性的子集,再从这个子集中选择最优划分属性,一般推荐K=log2(d)。
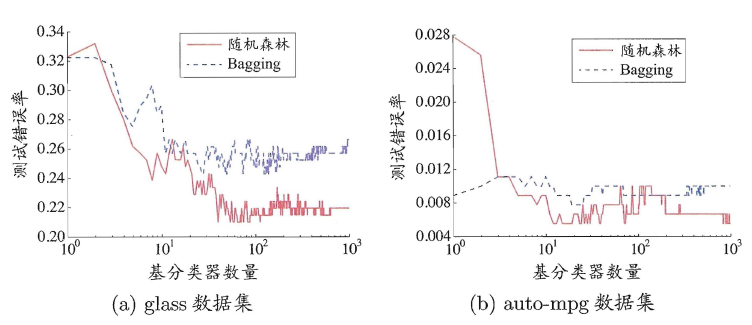
这样随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,从而进一步提升了基学习器之间的差异度。相比决策树的Bagging集成,随机森林的起始性能较差(由于属性扰动,基决策树的准确度有所下降),但随着基学习器数目的增多,随机森林往往会收敛到更低的泛化误差。同时不同于Bagging中决策树从所有属性集中选择最优划分属性,随机森林只在属性集的一个子集中选择划分属性,因此训练效率更高。
8.4 结合策略
结合策略指的是在训练好基学习器后,如何将这些基学习器的输出结合起来产生集成模型的最终输出,下面将介绍一些常用的结合策略:
8.4.1 平均法(回归问题)
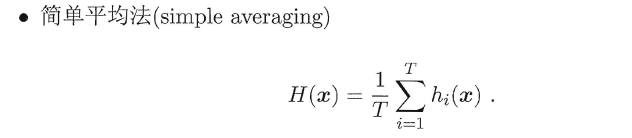
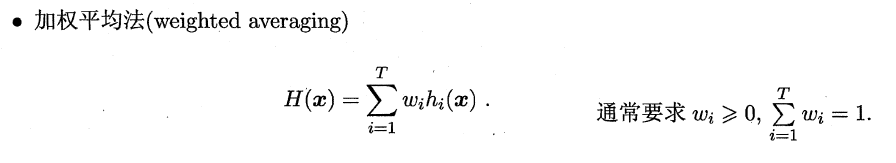
易知简单平均法是加权平均法的一种特例,加权平均法可以认为是集成学习研究的基本出发点。由于各个基学习器的权值在训练中得出,一般而言,在个体学习器性能相差较大时宜使用加权平均法,在个体学习器性能相差较小时宜使用简单平均法。
8.4.2 投票法(分类问题)

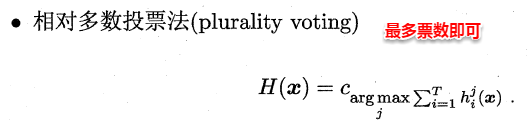
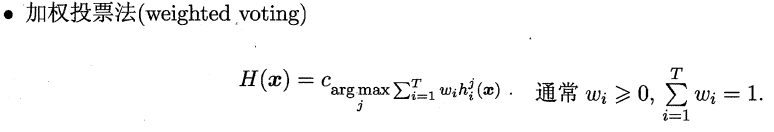
绝对多数投票法(majority voting)提供了拒绝选项,这在可靠性要求很高的学习任务中是一个很好的机制。同时,对于分类任务,各个基学习器的输出值有两种类型,分别为类标记和类概率。

一些在产生类别标记的同时也生成置信度的学习器,置信度可转化为类概率使用,一般基于类概率进行结合往往比基于类标记进行结合的效果更好,需要注意的是对于异质集成,其类概率不能直接进行比较,此时需要将类概率转化为类标记输出,然后再投票。
8.4.3 学习法
学习法是一种更高级的结合策略,即学习出一种“投票”的学习器,Stacking是学习法的典型代表。Stacking的基本思想是:首先训练出T个基学习器,对于一个样本它们会产生T个输出,将这T个基学习器的输出与该样本的真实标记作为新的样本,m个样本就会产生一个m*T的样本集,来训练一个新的“投票”学习器。投票学习器的输入属性与学习算法对Stacking集成的泛化性能有很大的影响,书中已经提到:投票学习器采用类概率作为输入属性,选用多响应线性回归(MLR)一般会产生较好的效果。

8.5 多样性
在集成学习中,基学习器之间的多样性是影响集成器泛化性能的重要因素。因此增加多样性对于集成学习研究十分重要,一般的思路是在学习过程中引入随机性,常见的做法主要是对数据样本、输入属性、输出表示、算法参数进行扰动。
数据样本扰动,即利用具有差异的数据集来训练不同的基学习器。例如:有放回自助采样法,但此类做法只对那些不稳定学习算法十分有效,例如:决策树和神经网络等,训练集的稍微改变能导致学习器的显著变动。
输入属性扰动,即随机选取原空间的一个子空间来训练基学习器。例如:随机森林,从初始属性集中抽取子集,再基于每个子集来训练基学习器。但若训练集只包含少量属性,则不宜使用属性扰动。
输出表示扰动,此类做法可对训练样本的类标稍作变动,或对基学习器的输出进行转化。
算法参数扰动,通过随机设置不同的参数,例如:神经网络中,随机初始化权重与随机设置隐含层节点数。
在此,集成学习就介绍完毕,看到这里,大家也会发现集成学习实质上是一种通用框架,可以使用任何一种基学习器,从而改进单个学习器的泛化性能。据说数据挖掘竞赛KDDCup历年的冠军几乎都使用了集成学习,看来的确是个好东西~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号