机器学习补充内容

神经网络模型

TCN：时域卷积网络

• (转载)时域卷积网络TCN详解：使用卷积进行序列建模和预测
• 《MS-TCN++》算法详解
• 机器学习进阶之 时域/时间卷积网络 TCN 概念+由来+原理+代码实现

---

• TCN（Temporal Convolutional Network，时间卷积网络）
• 论文《An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling》
• 时域卷积网络TCN详解：使用卷积进行序列建模和预测
• 时空卷积网络TCN：时空卷积网络TCN - USTC丶ZCC - 博客园
• Darts实现TCN(时域卷积网络）
• TCN-时间卷积网络:
• 多变量时间序列、预训练模型和协变量：
• 【论文阅读】An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling
• 【时序】基于 TCN 的用于序列建模的通用卷积和循环网络的经验评估

对应第三章 3.5

距离问题：

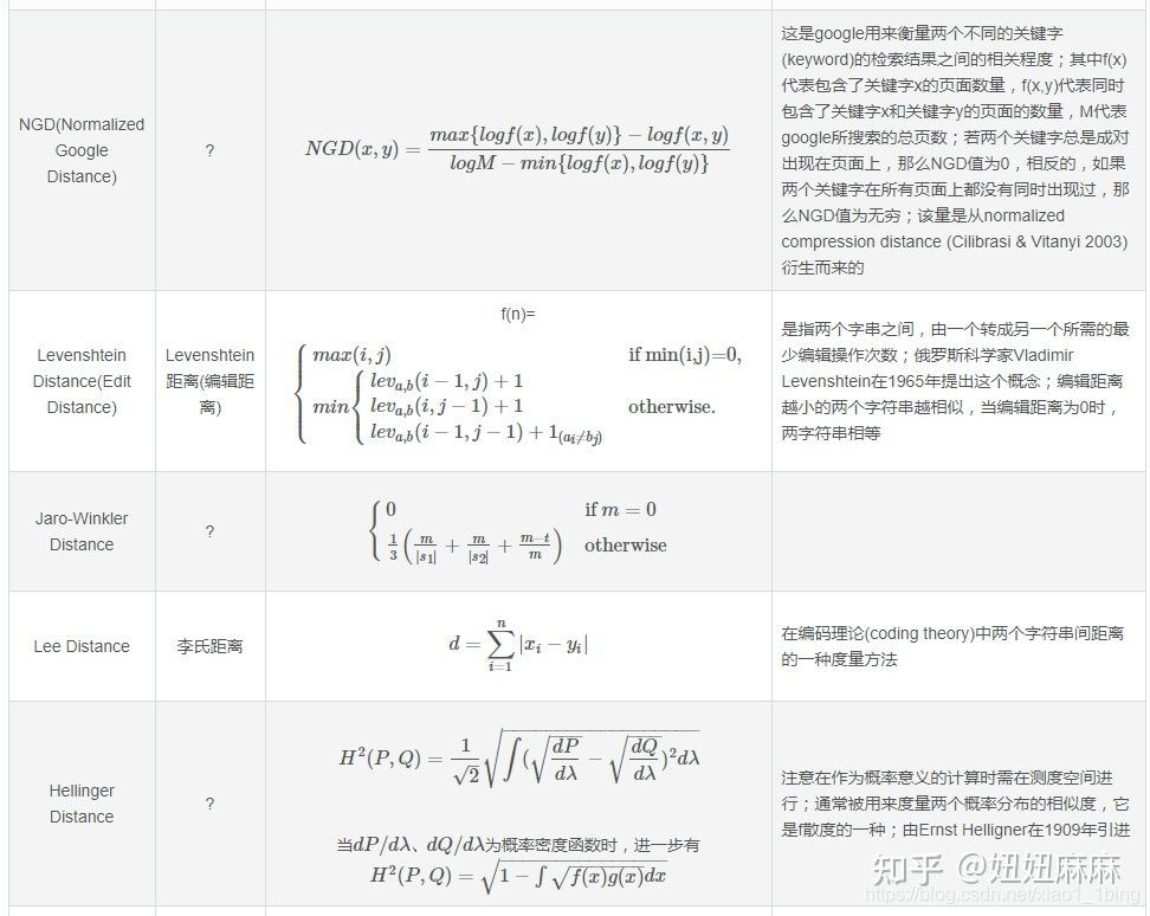
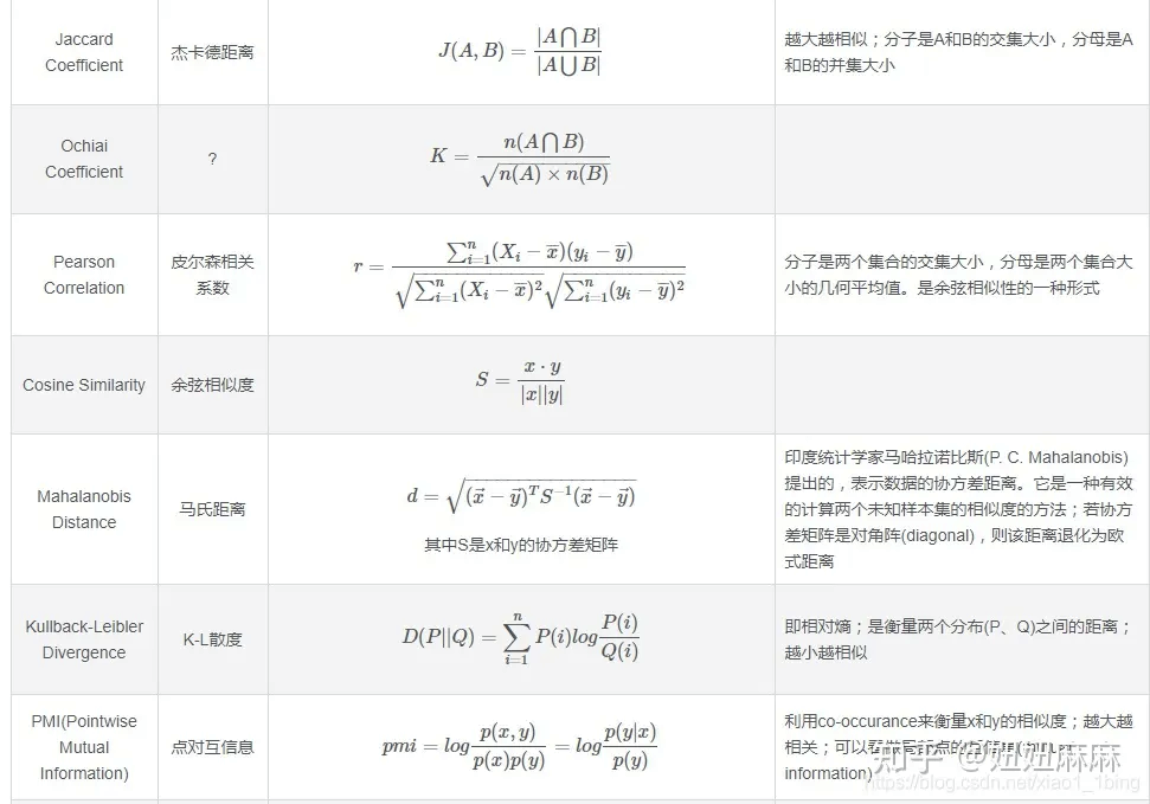
梯度下降法：

【如何通俗地解释梯度下降法】https://www.bilibili.com/video/BV1a94y1S7PP?vd_source=72c049a10a67579dd43376733253182c
【【梯度下降】3D可视化讲解通俗易懂】https://www.bilibili.com/video/BV18P4y1j7uH?vd_source=72c049a10a67579dd43376733253182c
https://zhuanlan.zhihu.com/p/580645925

要素：代价函数、起始点、梯度、学习率、截止条件

\[ 对一元来说:x_{k}=x_{k-1}-\eta\bigtriangledown f(x_{k-1})，\eta 为学习率，直到梯度小于某个数截止 \\对多元来说:(x_{k},y_{k},..)=(x_{k-1},y_{k-1},..)-\eta \bigtriangledown f(x_{k-1},y_{k-1},....),直到梯度小于某个数截止 \]

代码实践：http://localhost:8888/notebooks/Machine Learning note/梯度下降.ipynb

---

批量梯度下降法（BGD）：每次都把周围都扫一遍，然后找最低的往下走。更精准，但是慢。可以保证全局最优。

随机梯度下降法（SGD）：每下降一步只用一个样本，看一眼就往下走。变快了，但是精准度下降。不能保证全局最优。

小批量梯度下降法（MBGD）：看一部分再往下走，兼容了快速和精准度。也叫最速下降法。但也可能发生学习率过大反复横跳和学习率过小浪费算力的问题。也不能保证找到全局最优。

熵等概念补充

熵

问题：假设我们知道一个随机事件的概率分布。
1、我们如何度量其不确定性？
2、如何量化表示他相当于有多少种选择？
3、不同分布的随机事件，纠结程度如何比较？

线性回归与逻辑回归

机器学习相关的知识，逻辑回归的目的是什么？和线性回归有啥不同

逻辑回归和线性回归是两种不同的机器学习算法，它们用于不同的问题和具有不同的目的。

1. 目的：

   • 线性回归的主要目的是建立一个线性模型，用于预测一个连续数值输出（因变量）与一个或多个特征（自变量）之间的关系。它在回归问题中广泛用于预测、拟合和建模，例如，房价预测、销售量预测等。
   • 逻辑回归的主要目的是用于二元分类问题，即将观测值分为两个不同的类别或标签（通常为0和1）。逻辑回归通过建立一个S形曲线，将输入特征映射到一个介于0和1之间的概率值，表示观测值属于某一类的概率。逻辑回归通常用于问题如垃圾邮件分类、疾病诊断、用户流失预测等二元分类任务。

2. 输出类型：

   • 线性回归的输出是连续的实数值，可以在整个实数范围内变化。
   • 逻辑回归的输出是概率值，通常在0到1之间，表示观测值属于某一类别的概率。

3. 模型形式：

   • 线性回归使用线性函数，其形式为 y = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ，其中 y 是连续的因变量，β₀, β₁, β₂, ... βₙ 是模型参数。
   • 逻辑回归使用逻辑函数（也称为S形曲线或sigmoid函数），其形式为 p(y=1) = 1 / (1 + e^-(β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ))，其中 p(y=1) 是观测值属于类别1的概率，e 是自然对数的底数，β₀, β₁, β₂, ... βₙ 是模型参数。

4. 应用领域：

   • 线性回归通常用于解决回归问题，其中目标是预测或建模连续数值的输出。
   • 逻辑回归通常用于解决分类问题，其中目标是将观测值分为两个不同的类别或标签。

总之，逻辑回归和线性回归在目的、输出类型、模型形式和应用领域上都有明显的差异，因此它们适用于不同类型的问题。

深度学习概念

卷积长度：

 卷积操作中的卷积长度（也称为感受野大小），是指一个给定神经元(或输出特征图中的一个位置)受到输入图像或特征图的影响的区域大小。它决定了每个神经元对输入的响应以及它的特征提取能力。
卷积长度的计算取决于以下几个因素：
1、卷积核大小：这是卷积核的尺寸，通常表示为H×W(长*宽)
2、步幅：步幅是卷积核在输入上滑动的距离
3、填充：填充是输入图像周围添加零值像素的操作，以控制输出特征图的尺寸。

卷积长度计算公式：

\[ 一维： 卷积长度=\big(\frac{输入大小-卷积核大小+2×填充}{步幅}\big)+1 \\ 二维:与一维相似，只是涉及长、宽两个维度 \\ 输出高度=\big(\frac{输入高度-卷积核高度+2×垂直填充}{垂直步幅}\big)+1 \\ 输出宽度=\big(\frac{输入宽度-卷积核宽度+2×水平填充}{水平步幅}\big)+1 \]

RBG图像卷积示例：

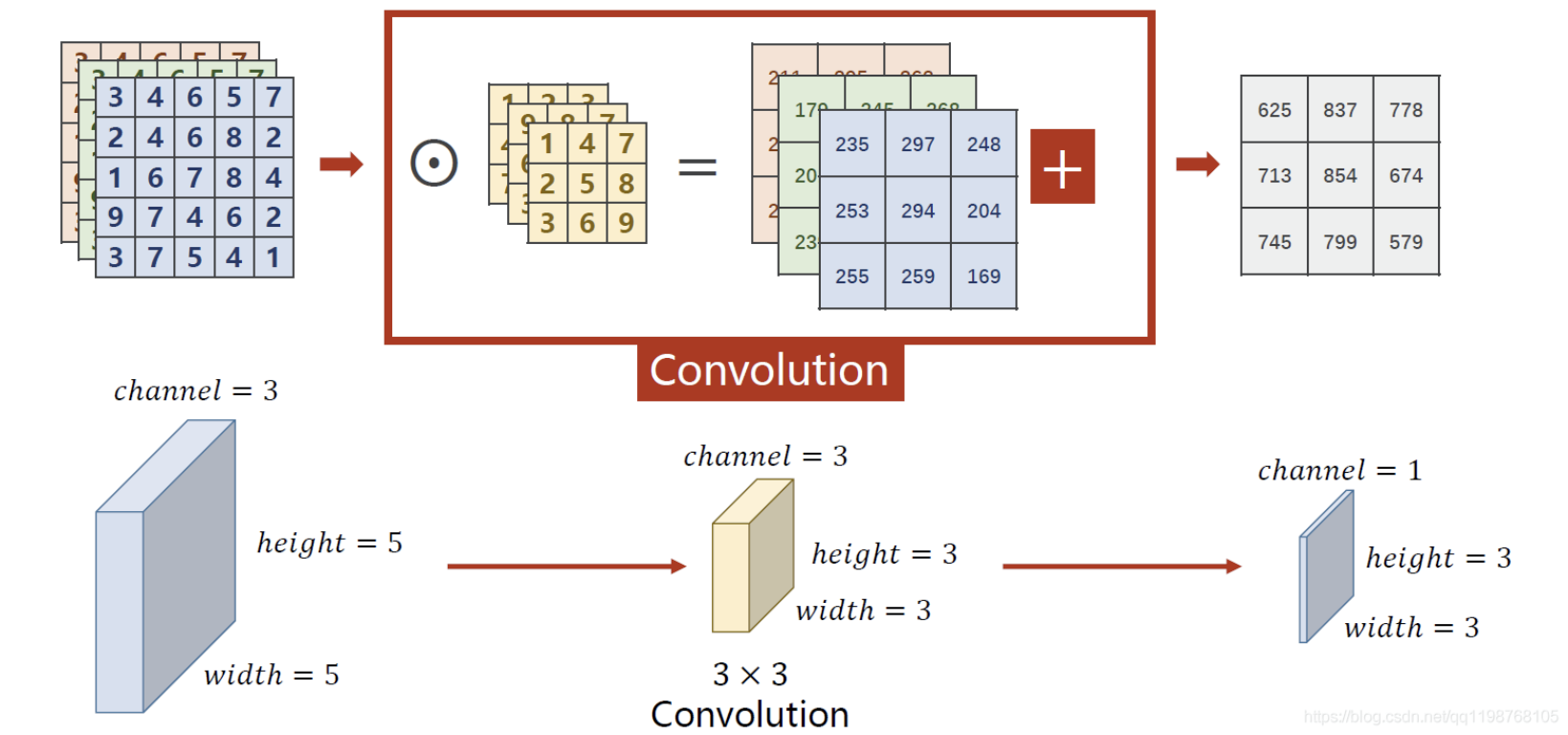
实例分割跟语义分割的区别：

• 实例分割就像给图片中的每个对象戴上穆面具一样。它不仅可以告诉你有哪些不同的对象（比如人、狗、车等），还能够准确地分辨出不同的人、不同的狗、不同的车，就像给每个对象一个独一无二的标签。

• 语义分割则类似于给图片的不同部分涂上颜色，告诉你每个像素属于图像中的哪个类别。比如，将所有道路像素标为蓝色、所有树木像素标为绿色等。但它不会区分道路上的不同车辆或者树木的种类。

 总的来说，实例分割会为每个对象提供一个独特的标识，而语义分割更关注图像中不同区域的整体分类。
确切来说：

1、实例分割：

• 实例分割不仅可以识别图像中的不同对象类别，还能够对每个对象实例进行像素级别的分割。
• 每个检测到的对象都被分配一个唯一的标识，并且对其进行像素级别的标记。这使得同一类别的不同对象之间可以进行区分。
• 实例分割旨在准确检测图像中的多个对象，并为每个对象提供独特的边界框和像素级别的分割标识。

2、语义分割：

• 语义分割侧重于将图像中的每个像素分配到预定义的语义类别中，不考虑不同对象实例之间的差异。
• 它的目标是为图像中的每个像素分配一个语义类别标签，例如“道路”、“汽车”、“树木”等，以实现对图像的整体语义理解。

在总体目标方面，实例分割着重于对图像中的不同对象实例进行精确定位和分割，而语义分割侧重于将图像像素分配到不同的语义类别中。

车道线检测传统方法为什么依赖手工设计的特征

传统方法在车道检测中主要依赖手工设计的特征，这意味着算法的车道检测性能主要依赖人类专家根据道路图像设计的特征或规则。这些特征通常基于基本的图像处理技术和几何学原理，如边缘检测、线段检测、颜色或纹理信息等。
这种依赖手工设计的特征的原因是传统方法的算法架构和特征提取步骤需要手动设计和定义。通过使用这些手动设计的特征，算法可以识别车道线或图案。这些特征可以是根据车道的几何形状、颜色、对比度、边缘等规则设计的。

传统方法依赖手工设计的特征存在以下限制：
复杂场景表现不佳： 对于复杂的交通场景，如遮挡、阴影、恶劣天气等，手动设计的特征不够灵活，容易受到外部环境的影响而表现不佳。
不适应大量变化： 传统方法可能难以适应不同道路和车道标志的变化，因为它们需要人为干预来适应新的情况。
特征提取难度： 由于车道的特征复杂多样，手动设计的特征提取需要充分理解道路图像，这是一项复杂且耗时的任务。

因此，随着深度学习的发展，人们逐渐使用卷积神经网络等技术，不再依赖手工设计的特征。深度学习的优势在于它可以自动地从数据中学习特征，从而提高了对复杂场景的适应性，并减轻了人工干预的需求。

参考资料

• 深度学习中的一些基本概念

什么是端到端？

"端到端"（End-to-End）是指一个系统或方法能够直接处理完整的任务，而不需要分解为多个阶段或组件。在计算机科学和机器学习领域，端到端方法强调通过一个统一的模型或系统来解决整个问题，而不是将问题分解为多个子任务并分别处理。
具体而言，端到端学习的核心思想是通过训练一个端到端模型，直接从原始输入数据到最终输出结果进行映射，而无需手动设计中间步骤或特征。这与传统的流水线方法（pipeline approach）不同，后者通常包含多个离散的阶段，每个阶段负责任务的一部分。

Transformer的关系建模能力？

1、序列建模能力

Transformer最初应用在NLP任务上，具有强大的序列建模能力。

2、关系建模

关系建模通常涉及对输入序列进行编码以捕获实体之间的复杂关系。Transformer 的注意力机制是它成功的关键组成部分之一，它允许模型在处理输入序列时聚焦于不同位置的信息。这使得 Transformer 能够有效地捕获输入序列中的长距离依赖关系，并在建模实体之间的关系时表现出色。

Transformer中注意力权重计算为什么是二次函数？

在自注意力机制（Scaled Dot-Product Attention）中，计算注意力权重的步骤包括计算查询（Query）和键（Key）之间的相似性，然后通过 Softmax 函数获取最终的注意力权重。

1、计算相似性： 对于一个输入序列或图像中的像素集合，每个位置（或像素）都需要与所有其他位置计算相似性。如果我们有N个位置（像素），那么对于每个位置，都需要计算与其他N-1个位置的相似性。因此，总的相似性计算次数是N * (N-1)。

2、Softmax 操作： 接下来，对于每个位置，需要将相似性转化为概率分布，这通常通过应用 Softmax 函数完成。Softmax 函数的计算涉及对相似性值进行指数运算，这也是一个与序列长度（或像素数量）相关的操作。

总的计算复杂度由相似性计算和 Softmax 操作共同决定。因为对于每个位置，都需要与其他位置计算相似性，并且 Softmax 操作与序列长度（像素数量）相关，所以总的计算复杂度是二次的，与序列长度（像素数量）的平方成正比。

Deformable convolution 为什么确实元素关系建模机制？

Deformable Convolution（可变形卷积）是一种卷积神经网络（CNN）中的卷积操作，通过允许卷积核内部的采样点位置进行变形，从而提高了模型对目标的建模能力。这种卷积操作的提出是为了更好地适应目标在图像中的非刚性形状和局部变形。

然而，Deformable Convolution 在处理元素关系建模时可能缺少一些机制，这可能由其设计原理和主要用途决定：

1、局部感受野： Deformable Convolution 主要关注局部区域内的特征建模，通过在卷积核内引入可变形采样点，可以提高模型对局部变形的适应性。然而，它的设计并没有直接引入全局元素关系建模的机制。

2、元素关系建模： Deformable Convolution 的设计目标更倾向于处理空间局部的变形，而不是直接建模元素之间的全局关系。在某些任务中，特别是涉及全局上下文信息和元素之间长距离关系的任务，可能需要额外的机制来更好地捕捉元素之间的关系。

3、任务特定性： Deformable Convolution 的使用通常取决于具体任务和应用场景。对于一些任务，例如目标检测，局部变形建模可能是更为关键的，而对于其他任务，例如图像分类，全局元素关系建模可能更为重要。

虽然 Deformable Convolution 本身可能不直接包含全局元素关系建模的机制，但研究人员可以通过将其与其他注意力机制或全局建模方法结合使用，以满足任务的特定需求。例如，可以通过在网络中引入全局信息注意力机制（如Transformer中的自注意力机制）、多尺度特征融合、全局池化、位置编码的改进来更好地捕获元素之间的全局关系。