机器学习-周志华(5-6章)

第5章 神经网络

5.1 神经元模型

基本单元：神经元
灵感来源：
 生物神经网络（1、当神经元“兴奋”时，向相邻的神经元发送化学物质，从而改变相邻神经元的电位）
 激活：如果某个神经元的电位超过了一个“阈值”，那么它就会被激活，即“兴奋”起来，向其他相邻神经元发送化学物质。
图例：McCulloch和Pitts于1943年将上述情况抽象为数据模型，即神经元模型（M-P神经元模型）

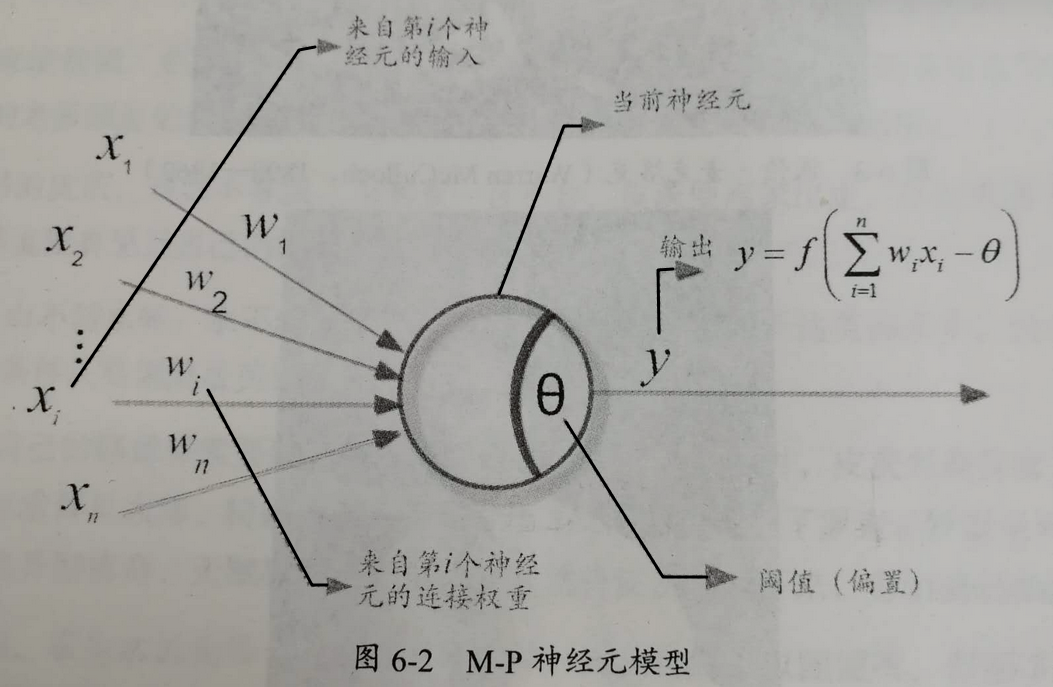
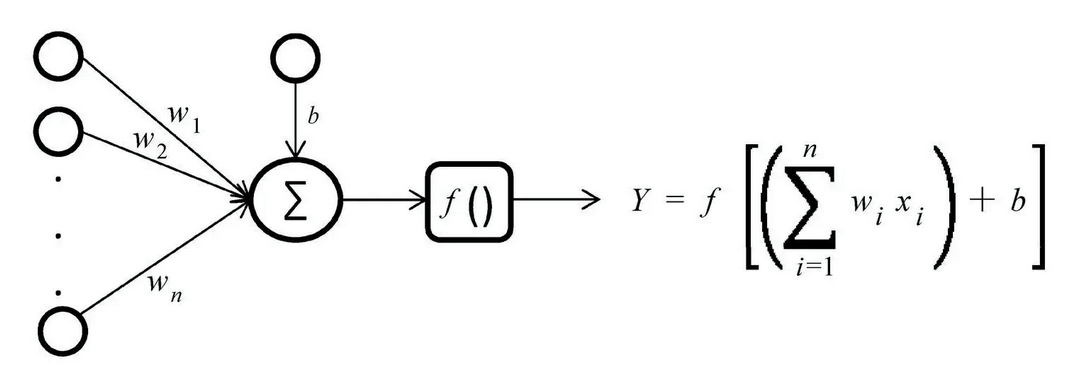
公式表:

\[y=f \big(\sum_{i=1}^{d}w_{i}x_{i}+b\big) \\d是样本维度；w权重个数与样本维度相等； \\f(*)激活函数或激励函数，sign(x)=\begin{cases}1,x \geq0\\0,x <0 \end{cases} \\输出结果：1、样本与权重相乘；2、再与阈值相加；3、通过激活函数得到 \]

5.2 感知机与多层网络

一个感知机：神经网络之所以能够以任意精度拟合任意复杂的连续函数的一个重要原因是因为感知机可以非常容易地实现逻辑与、或、非运算
特点：

• 感知器模型非常容易解决线性问题
• 非线性问题，如异或问题，无法采用一个感知器模型将其完全分离
• 如果采用两个感知器模型，则每个感知器模型只学习一个线性分界线，然后通过逻辑与运算，取两部分的并集就能将异或问题完美解决
• 神经网络模型沿用了这种思想，增加感知器的方式在原始空间解决非线性分类

两个感知机：

异或问题：
需要注意的是，由于感知器模型得到的分界线并不是唯一的。因此，由感知器组成的神经网络模型的学习结果也不是唯一的。所以，求与运算得到的结果可能有多种形式。

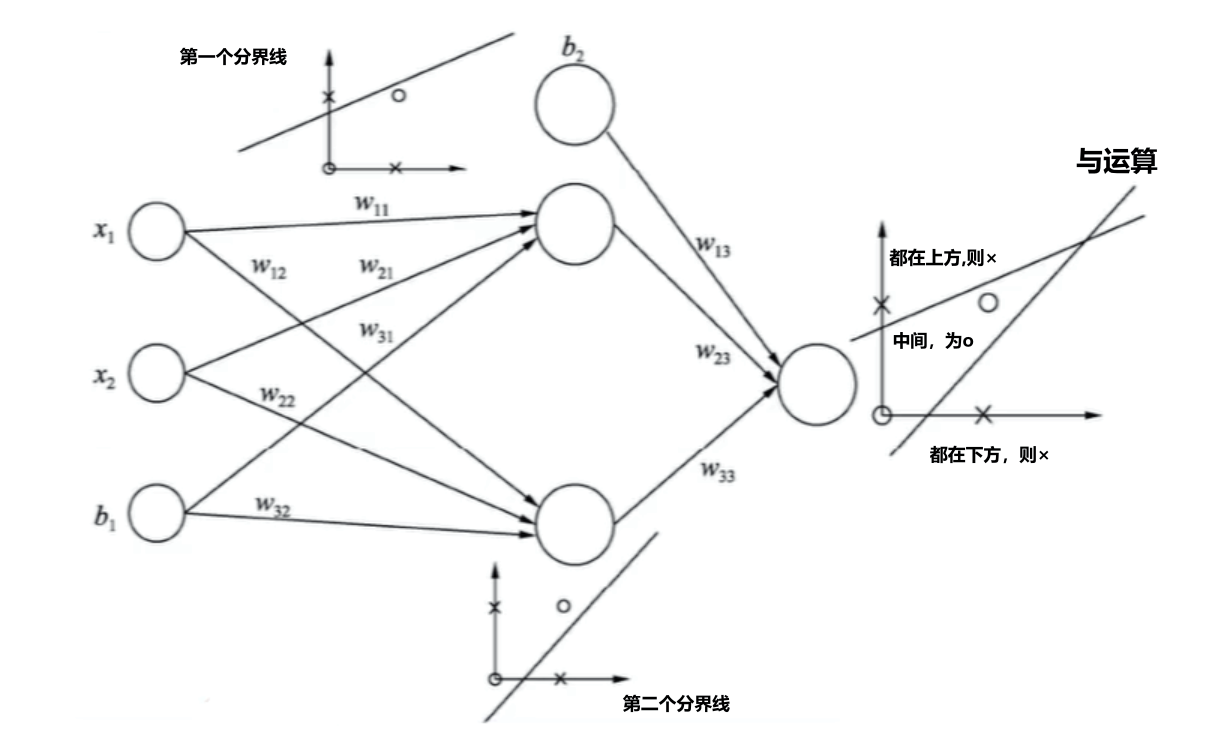
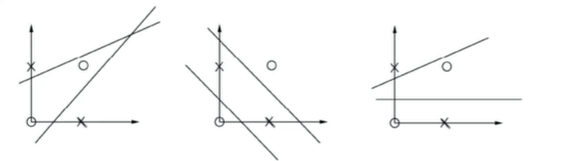
神经网络：

多个感知器模型组成了神经网络模型
神经网络中随着感知器的增加其模型的表达能力也会增强

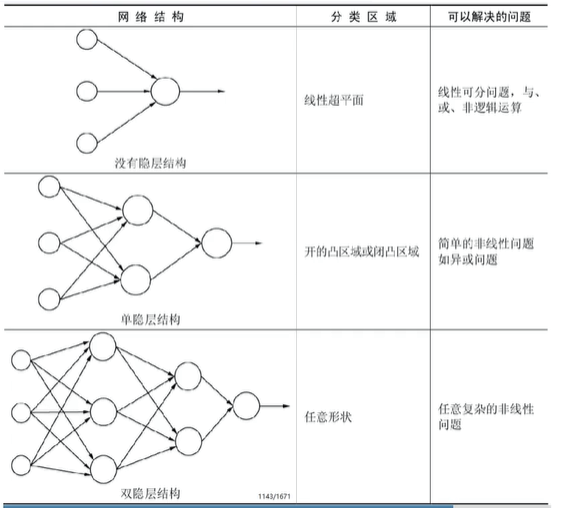
以单隐层结构为例：分别采用了1、5、50个隐层节点，分类边界从直线逐渐变为非常平滑的曲线，可见神经网的学习能力是非常强大的。

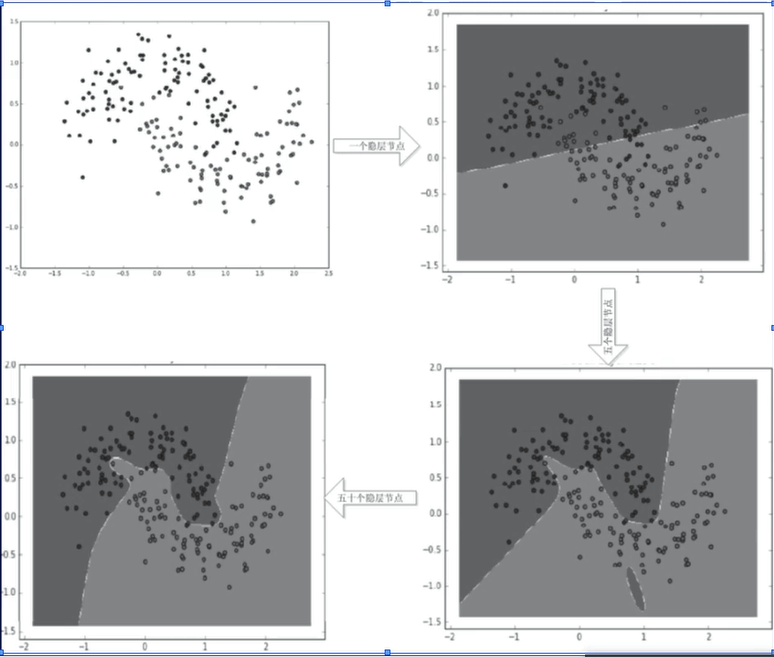
多层前馈神经网络

模型：

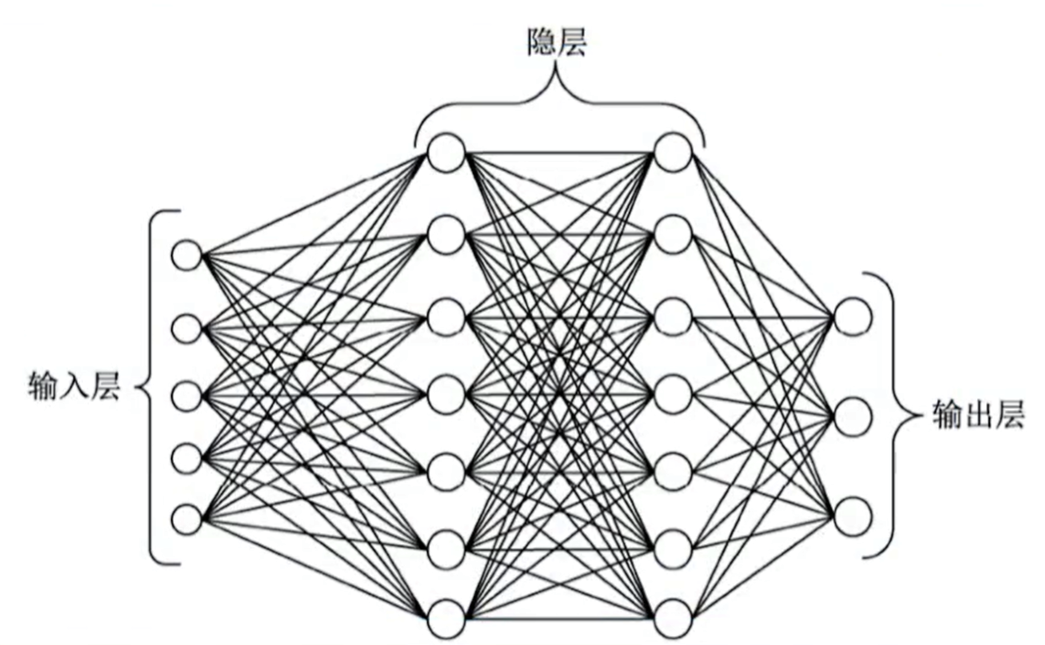
输入层（第一层）：没有激活函数，只是将输入信号传递给隐层的神经元

---

输出层（最后一层）：1、有激活函数；2、负责将中间层的结果加权，实现不同的逻辑；3、运算并得到最后的预测结果

---

中间层（隐层）：
1、有激活函数；
2、隐层可以有多层，每层中可以有多个神经元；
3、隐层中第一层的每一个神经元都与前一层（输入层）的所有神经元构成一个感知器模型（也是逻辑回归模型）
4、同样隐层的第二层的每一个神经元都与前一层（隐层的第一层）的所有神经元构成一个感知器模型

---

连接方式：
1、前馈网络是指每层的神经元与下一层的神经元以全连接的形式互联
2、同层的神经元之间不存在连接
3、跨层的神经元之间不存在跨层连接

---

参数个数：
参数位置：输入层与隐层之间有权重；隐层与隐层之间有权重；隐层与输出层之间有权重
假设：输入数据的维度为m，采用双隐层网络（第一个隐层有n个节点，第二个隐层有t个节点）；输出层有s个神经元
故权重个数：\(sum(w)=(m+1)*n+(n+1)*t+(t+1)*s\),加一是由于每个神经元都有一个偏置项b.

5.3 误差逆传播算法

5.4全局最小与局部极小

5.5 其他常见神经网络

5.6 深度学习

5.7 阅读材料

参考资料

• 斋藤康毅 （深度学习入门、深度学习进阶、框架学习、强化学习）

第6章 支持向量机

6.1 感知器模型

给定训练集\(D={(x_{1},y_{1}),...,(x_{N},y_{N})},y_{i}=\{-1,+1\}\)

目标：基于训练集D在样本空间找到一个划分超平面，将不同类别的样本分开。

数据：训练集D;样本个数N；一个样本\(x_{i}^{T}=(x_{i1},x_{i2},...,x_{id})\)为第i个输入样本；特征个数d（特征个数组成样本空间）;

划分超平面的方程表述：

\[ w^{T}x+b=0, \\其中w=\{ w_{1};w_{2};...;w_{d}\}为法向量，决定了超平面的方向 \\b为位移项，决定了超平面与原点之间的距离 \]

模型:\(y=f\big(w^{T}+b\big)\)
 w为权重，个数与输入变量x的维度相同；
 f(*)为映射函数，比如\(sign(x)=\begin{cases} +1,x\geq 0 \\-1,x<0\end{cases}\)

训练：

\[ \begin{cases} 当w^{T}x+b\geq 0时，输出预测值\hat{y}=+1\\ 当w^{T}x+b< 0时，输出预测值\hat{y}=-1 \end{cases} \]

训练下的预测值与真实值的关系：

\[分类错误情况： \begin{cases} 当预测值为+1，即\hat{y}=+1，真实值为-1,即y=-1;那么y*\hat{y}=-1\\ 当预测值为-1，即\hat{y}=-1，真实值为+1,即y=+1;那么y*\hat{y}=1 \end{cases} \\ 分类正确情况： \begin{cases} 当预测值为+1，即\hat{y}=+1，真实值为+1,即y=+1;那么y*\hat{y}=1\\ 当预测值为-1，即\hat{y}=-1，真实值为-1,即y=-1;那么y*\hat{y}=1 \end{cases} \\ 其中，\hat{y}=w^{T}x+b \]

训练中的损失函数：

• 对于所有分类错误的样本M，将\(y(w^{T}x+b)\)作为损失函数
• 变号:由于分类错误，则\(y(w^{T}+b)\lt 0\),我们需要这个式子接近0，相当于是最大化值，而损失函数一般都是求最小值，所以加个负号，因此，将\(-y(w^{T}+b)\lt 0\)作为损失函数。
• 最终。损失函数的表达式为：$ L(w,b)=- \sum_{x_{i}\in M}y\big(w^{T}x+b\big) $

求解w,b方法：梯度下降法

• 求导：

\[\nabla_{w}L(w,b)=-\sum_{x_{i}\in M} y_{i}x \\ \nabla_{b}L(w,b)=-\sum_{x_{i}\in M}y_{i} \]

• 初始化:随机分类错误点\(w_{0},b_{0}\)
• 计算梯度
• 对参数进行更新

\[ w_{1}=w_{0}-(-\eta y_{i}x_{i})=w_{0}+\eta y_{i}x_{i} \\ b_{1}=b_{0}+\eta y_{i} \]

• 多次迭代得到w和b

支持向量机的分类:

1、样本是线性可分的---线性可分支持向量机(Linear Support Vector machine in Linearly Separable Case)
技巧：硬间隔最大化(选出最优平面）

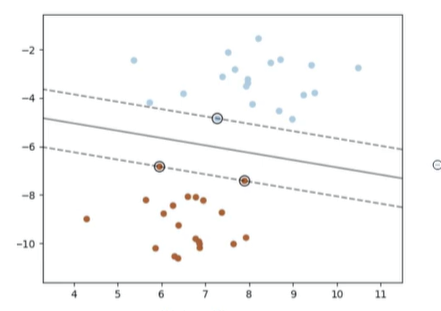
线性可分

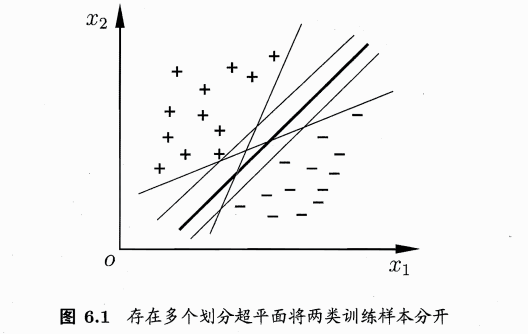
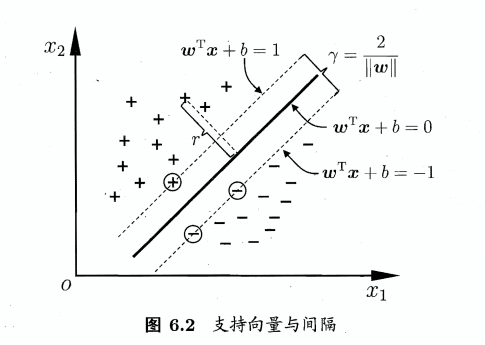
问题：在如下图中的众多超平面中，哪个是最佳超平面?

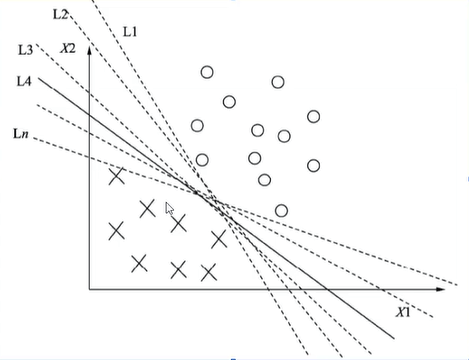
解决思路：

直观上：
1、位于两类样本中间的划分超界面最好；
2、多一个，少一个样本，获得的超平面不会变,即这个划分超平面对训练样本的容忍性最好

理性上：
1、考虑用样本到平面的距离来衡量平面
2、距离远的容易被分类，距离近的不容易被分类

模型：
第一步：公式：\(f(x)=sign(w^{T}x+b)\)，在上图中，超平面上方，被分类成正例，反之，被分类成反例。
第二步：计算距离：所有样本到超平面的距离\(dist_{i}=\frac{|w^{T}x_{i}+b|}{||w||}\cong \frac{y{i}\big(w^{T}x+b\big)}{||w||}\)

如何去的绝对值?根据 分类正确的样本，同乘结果为整数；分类错误的样本，同乘结果为负数。

为什么距离能为负数？距离为负数表明分类错误，样本出现在不该出现的区域。

第三步：获取距离最小值：获取所有样本点中 距离的最小值，\(\gamma=min\frac{y\big(w^{T}x+b\big)}{||w||}\space 式（1），即\frac{y\big(w^{T}x+b\big)}{||w||}\geq \gamma\space 式(2)\)

(2)式表达了 只要最小距离的样本被正确分类，那么最小距离大于0 等价于 其他所有样本一定被正确分类；这会出现多个划分平面满足这个条件。

第四步：选择最佳平面：N个超平面满足最小距离大于0,则有N个最小距离。只需在这些最小距离中找到一个最大的\(\upsilon\)，即该\(\upsilon\)代表的划分平面离两类的距离最远。

\[ 最优超平面=arg\space max_{w,b}\big(min \frac{y\big(w^{T}x+b\big)}{||w||}\big)=arg\space max_{w,b}\gamma \\s.t. \frac{y_{i}\big(w^{T}x_{i}+b\big)}{||w||} \geq \gamma,i=1,2,..,N \]

第五步：最佳平面唯一表达式：

• 当w与b等比例改变时，平面不变，距离不变，平面表达式改变

• 通过距离固定w,b

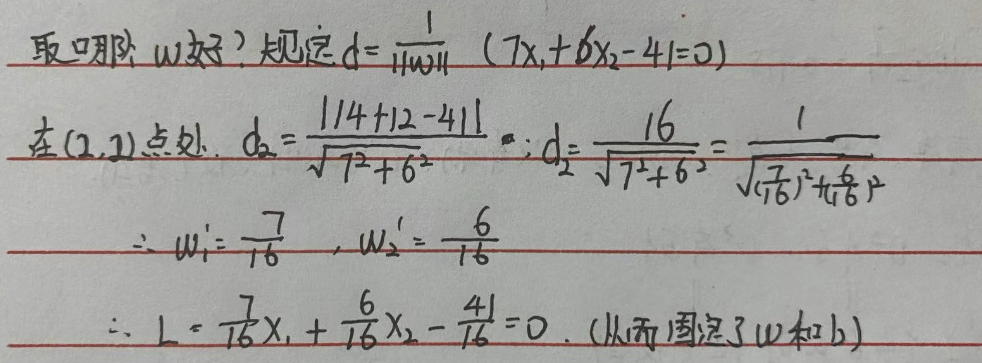
• 目标公式转换

第六步：问题转换
原问题：

\[ arg\space min_{w,b} \frac{1}{2}||w||^2 \space s.t.y_{i}(w^{T}x_{i}+b)\geq 1,i=1,2,...,N \\即凸二次优化问题，即求||w||的最小值下，w和b的值，且需要满足约束条件 \]

怎么求解凸二次优化问题？1、直接求解(效率低);2、采用拉格朗日对偶性,通过对偶问题得到更高效的求解方法
拉格朗日对偶性，即多个不等式约束下，求最小值问题；等等价于一个等式，求最小值问题

转换后的问题：
拉格朗日对偶性转换问题后的拉格朗日函数为：

\[ L(w,b,\alpha)=\frac{1}{2}||w||^{2}+\sum_{i=1}^{m}\alpha_{i}\big(1-y_{i}(w^{T}x_{i}+b)\big) \space\space (6.8) \\ 其中拉格朗日乘子：\alpha=(\alpha_{1};\alpha_{2};...;\alpha_{m})\\ 或者理解成max_{\alpha}min_{w,b} L(w,b,\alpha) \]

第7步：求解推导
求\(min_{w,b}L(w,b,\alpha)\):
1、对w和b分别求导：

\[ \frac{dL(w,b,\alpha)}{dw}=w-\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}\\ \frac{dL(w,b,\alpha)}{dw}=\sum_{i=1}^{m}\alpha_{i}y_{i} \]

2、令偏导数等于0，

\[ w=\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i} \space\space (6.9)\\ 0=\sum_{i=1}^{m}\alpha_{i}y_{i} \space\space （6.10） \]

3、将偏导数为0的结果带入到拉格朗日函数

\[\begin{align} L(w,b,\alpha)&=\frac{1}{2}||w||^{2}-\sum_{i=1}^{m}\alpha_{i}\big(y_{i}(w^{T}x_{i}+b)-1\big)\\ &=\frac{1}{2}w^{T}w-w^{T}\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}-b\sum_{i=1}^{m}\alpha_{i}y_{i}+\sum_{i=1}^{m}\alpha_{i}\\ &=\frac{1}{2}w^{T}\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}-w^{T}\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}-b*0+\sum_{i=1}^{m}\alpha_{i}\\ &=\sum_{i=1}^{m}\alpha_{i}-\frac{1}{2}\big(\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}\big)^{T}\sum_{i=1}^{m}\alpha_{i}y_{i}x_{i}\\ &=\sum_{i=1}^{m}\alpha_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j} \space\space（6.11） \end{align} \]

4、求$\alpha$的最大值
对（6.11）添加负号，将求最大值转变成求最小值
即将（6.11）转换成：\(arg\space_{\alpha} min \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}y_{i}y_{j}x_{i}^{T}x_{j}-\sum_{i=1}^{m}\alpha_{i}\space s.t. \sum_{i=1}^{m}\alpha_{i}y_{i}=0,\alpha_{i}\geq 0 ,i=1,2,...,m\)

SMO法求解：

第8步：求解过程

构造并求解约束最优化问题，式(6.11)
通过SMO方法优化\(\alpha\)，得到最优\(\alpha=(\alpha_{1},..,\alpha_{m})\)
计算w和b的值，w通过式(6.9),b通过\(b=y_{i}-\sum_{j=1}^{m}\alpha_{j}y_{j}x_{j}^{T}x_{i}\)
确定最终模型

2、样本近似线性可分---线性支持向量机(Linear Support Vector machine)
技巧：软间隔，松弛因子(放弃部分样本)

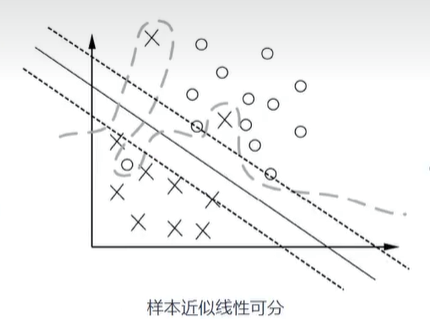
3、样本非线性可分--非线性支持向量机(Non-Linear Support Vector machine)
技巧：核函数（升维）

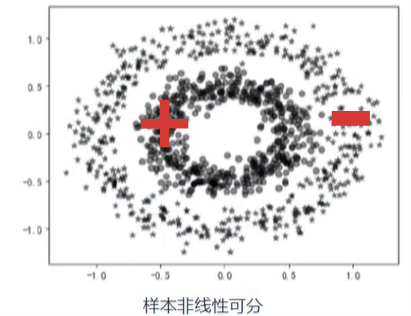
6.2 间隔与支持向量

样本空间中任意点x到超平面(w,b)的距离：

\[ r=\frac{|w^{T}x+b|}{||w||} \]

假设超平面(w,b)能将训练样本正确分类，即对于\((x_{i},y_{i})\in D\),若\(y_{i}=+1\)，则有\(w^{T}x_{i}+b>0\);若\(y_{i}=-1\)，则有\(w^{T}x_{i}+b<0\).令

\[ \begin{cases} w^{T}x_{i}+b\geq +1,y_{i}=+1\\ w^{T}x_{i}+b\leq -1,y_{i}=-1 \end{cases} (6.3) \]

距离超平面最近的训练样本点使(6.3)的等号成立，它们被称为"支持向量"。则两个异类支持向量到超平面的距离之和为\( \gamma=\frac{2}{||w||}(6.4)(利用两直线间距离公式) \),它被称为"间隔"

间隔最大划分超平面，受局部扰动的影响最小，故要求得最大间隔超平面的（w,b）,即

\[max_{w,b}\frac{2}{||w||} ,s.t. y_{i}(w^{T}x_{i}+b)\ge1, i=1,..,m (6.5) \]

为了最大化间隔，则仅需最大化\(||w||^{-1}\),等价与最小化\(||w||^{2}\)
故可改写成：

\[ min_{w,b} \frac{1}{2}||w||^{2},s.t. y_{i}(w^{T}x_{i}+b)\ge1, i=1,..,m （6.6） \]

上面这个式子也就是支持向量机（SVM）的基本型

s.t. 是subject to：满足的意思，在此处是满足所有样本被正确分类。

参考资料：https://zhuanlan.zhihu.com/p/101935149

6.3 对偶问题

6.4 核函数

样本空间向高维映射过程分析：

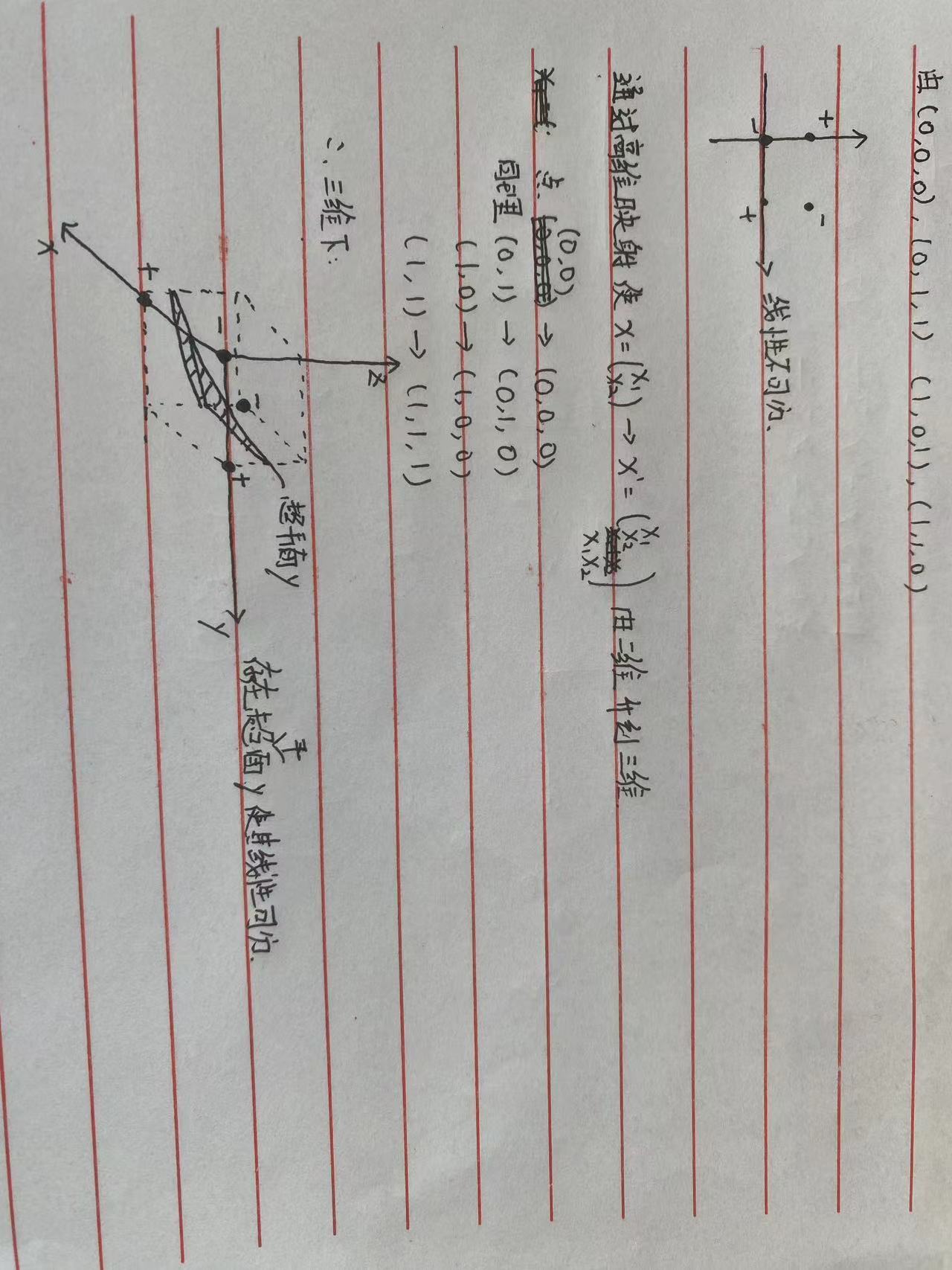
上图中，是通过对已有的特征进行组合，形成更多的特征。特征增加了，我们就更有可能增加样本的区分度，而且特征维度增加的越多，我们就越有机会让样本线性可分。

参考资料：
★高维映射 与 核方法
★★★★机器学习实战教程（八）：支持向量机原理篇之手撕线性SVM
样本空间向高维映射动画

6.5 软间隔与正则化

6.6 支持向量回归

6.7 核方法

6.8 阅读材料

6.9 补充材料

• SVM 本质是一个最大间隔的线性分类器

参考资料

• Python 金融大数据风控建模实战

上一章:3-4
下一章:7-8