机器学习-周志华(3-4章)
第3章 线性模型
3.1 基本形式
问题描述:给定由d个属性描述示例\(x=(x_{1};x_{2};...;x_{d})\),其中\(x_{i}\)是x自第i个属性上的取值,线性模型(Linear model)试图学得一个通过属性的线性组合来进行预测函数,即
函数描述:\(f(x)=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}+b\)
向量形式:\(f(x)=w^{T}x+b\),其中\(f(x)=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}+b\).w和b学得之后,模型就得以确认。
3.2线性回归
问题描述:给定数据集\(D=\{(x_{1},y_{1}),(x_{2},y_{2}),..,(x_{m},y_{m})\}\),其中\(x_{i}=(x_{i1};x_{i2};...;x_{id}),y_{i}\in \mathbb{R}\).“线性回归”(linear regression)试图学得一个线性模型以尽可能准确地预测实值输出标记,即线性回归试图学习\(f(x_{i})=wx_{i}+b\),使得\(f(x_{i})\approx y_{i}\)
如何确定w和b?
1、一元线性回归
关键在于如何衡量f(x)与y之间的差别,(均方误差是回归任务最常用的性能度量)。因此可试图让均方误差最小化,从而确定w和b
argument of the maximum/minimum
arg max f(x): 当f(x)取最大值时,x的取值
arg min f(x):当f(x)取最小值时,x的取值
"最小二乘法":基于均方误差最小化来进行模型求解的方法。即试图找到一条直线,使所有样本到直线上的欧氏距离之和最小。
确定w和b使均方误差最小的过程,称为线性回归模型的最小二乘"参数估计"(parameter estimation).
即通过对w,b求导确定最优解
最小二乘法的参数估计推导:

2、多元线性回归
关系式:\(f(x_{i})=w^{T}x_{i}+b\)
目标函数:

目标函数求解:



代码实践:https://github.com/Gievance/Python-MachineLearning/blob/master/Machine Learning note/多元线性回归.ipynb
高维问题可以使用梯度反向传播法,见3.7
3、对数线性回归
将模型预测值逼近y的衍生物,便有“对数线性回归”:

拓展:
更一般地,考虑单调可微函数g(·),令\(y=g^{-1}(w^{T}w+b)\),便得到“广义线性模型”
对数线性回归时广义模型在g(·)=ln(·)时的特例
3.3、对数几率回归(逻辑回归)
问题描述:
1、分类问题:将x的取值映射到固定的y空间内
2、线性模型进行的回归学习,对样本做了预测,但对分类问题而言,需要将预测值与真实标记联系起来。
3、通过广义线性模型,用一个单调可微的联系函数将预测值y做个转换,映射到标记空间。
实例:二分类任务
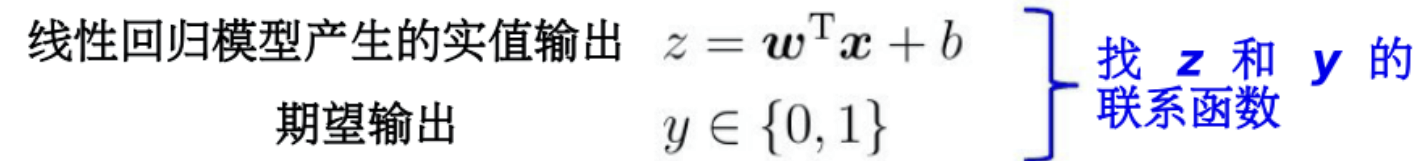
单位阶跃函数不连续,对数几率函数单调可微故可做联系函数
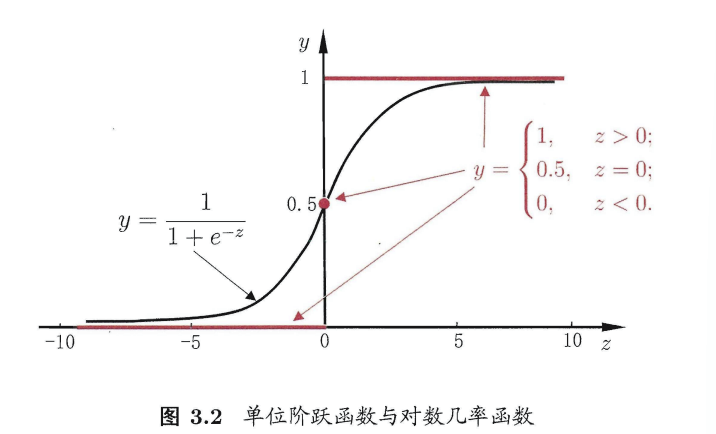
函数形式:
几率:\(\frac{y}{1-y}\),y视为样本的正例可能性,1-y视为样本的反例可能性
对数几率:\(ln\frac{y}{1-y}\)
在对数几率回归模型下,如何确定w和b?
极大似然估计法
小结:
1、利用线性回归模型的预测结果去逼近真实标记的对数几率,其对应的模型称为“对数几率回归”
2、logistic回归是一个分类算法,它可以处理二元分类以及多元分类。首先逻辑回归构造广义的线性回归函数,然后使用sigmoid函数将回归值映射到离散类别。
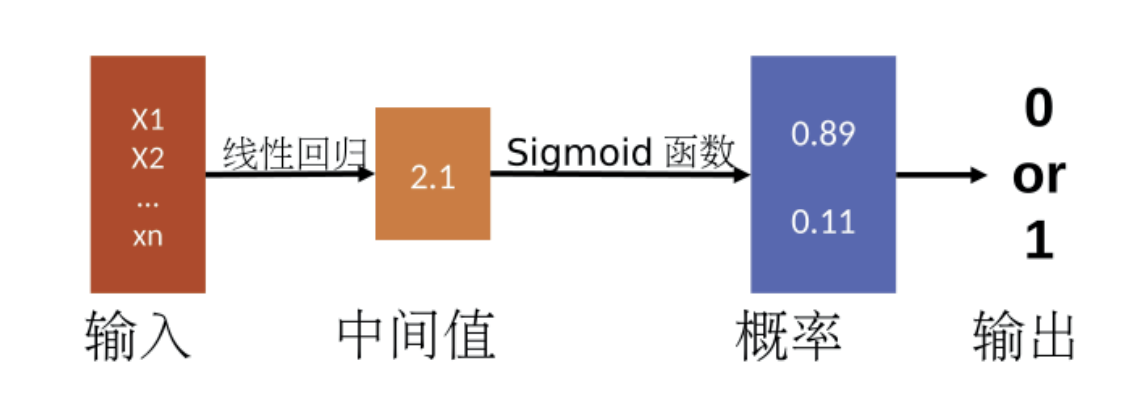
3.4 线性判别分析
LDA=Linear Discriminant Analysis=Fisher判别分析
基本思想:
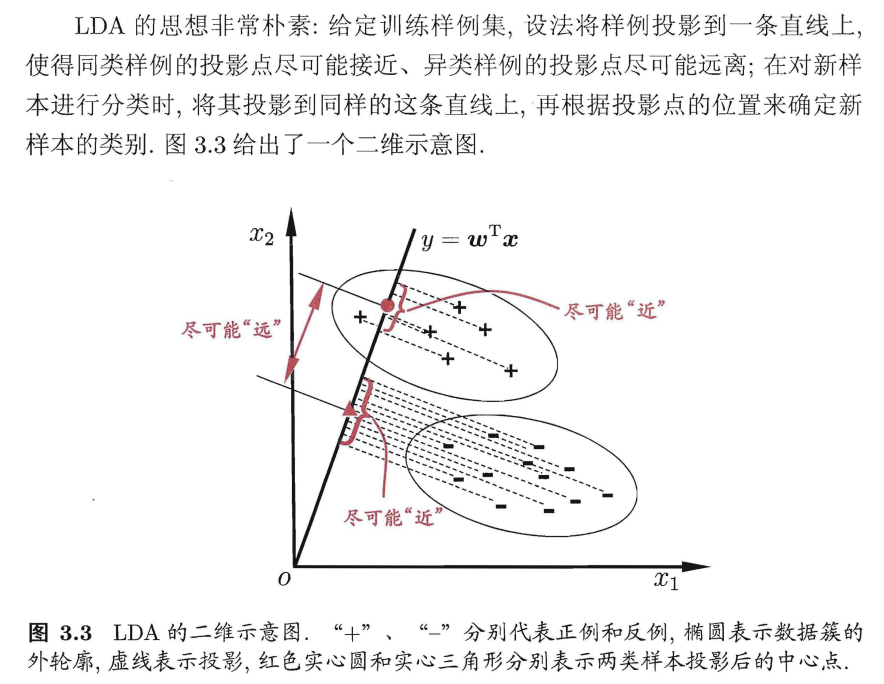

想让同类样本点的投影点尽可能接近,不同类样本点投影之间尽可能远,即:让各类的协方差之和尽可能小,不用类之间中心的距离尽可能大。基于这样的考虑,LDA定义了两个散度矩阵。
- 类内散度矩阵(within-class scatter matrix)
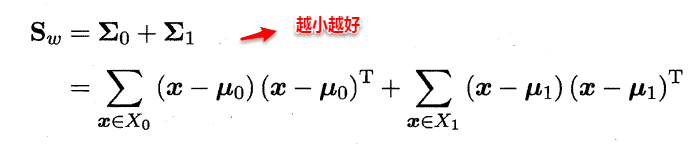
- 类间散度矩阵(between-class scaltter matrix)
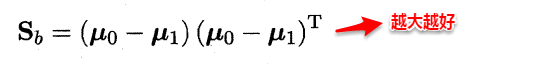
因此得到了LDA的最大化目标:“广义瑞利商”(generalized Rayleigh quotient)。
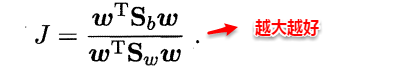
从而分类问题转化为最优化求解w的问题,当求解出w后,对新的样本进行分类时,只需将该样本点投影到这条直线上,根据与各个类别的中心值进行比较,从而判定出新样本与哪个类别距离最近。求解w的方法如下所示,使用的方法为λ乘子。

若将w看做一个投影矩阵,类似PCA的思想,则LDA可将样本投影到N-1维空间(N为类簇数),投影的过程使用了类别信息(标记信息),因此LDA也常被视为一种经典的监督降维技术。
3.5多分类学习
基本思路:“拆解法”将多分类任务拆为若干个二分类任务求解。具体来说,先对问题进行拆分,然后为拆出的每个二分类任务训练一个分类器;在测试时,对这些分类器的预测结果进行集成以获得最终的分类结果。
经典的拆分策略:
1、OvO(一对一:one vs one)
OvO给定数据集\(D={(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n}),}, y_{i}=\{ C_{1},C_{2},...,C_{N} \}\) ;OvO将这N个类别两两配对,从而产生N(N-1)/2个二分类任务。
2、OvR(一对其余:one vs rest)
OvR每次将一个类的样例作为正例,所有其他类的样例作为反例来训练N个分类器;在测试时若仅有一个分类器预测为正类,则对应的类别标记作为最终分类结果。
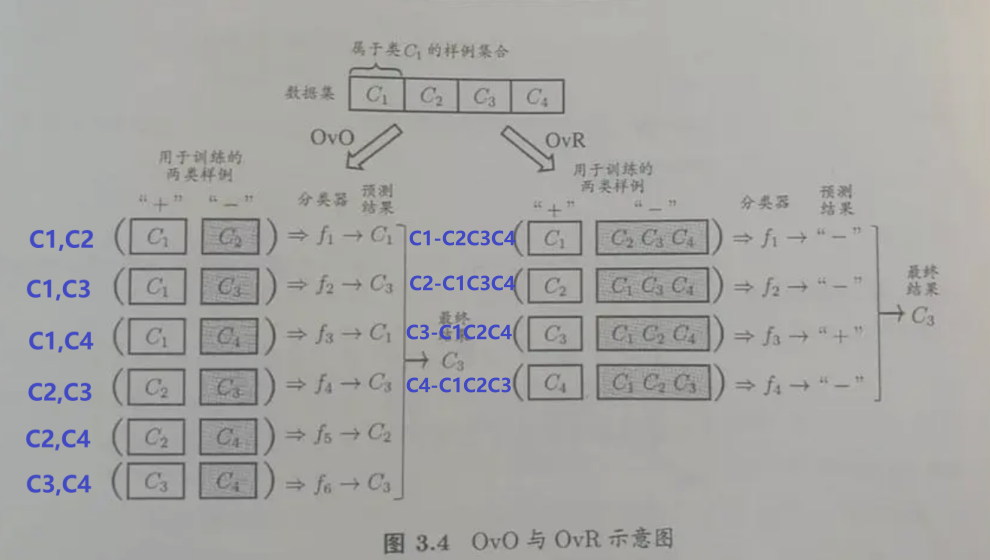
3、MvM(多对多:Many vs Many)
MvM每次将若干个类作为正类,若干个其他类作为反类。OvO和OvR是MvM的特例。MvM的正、反例构造必须有特殊的设计(比如:“纠错输出码”,(Error Correcting Output Codes:ECOC))
ECOC将编码的思想引入类别拆分,并尽可能在解码过程中具有容错性。
- 编码:对N个类别做M次划分,每次划分将一部分类别划为正类,一部分划分为反类,从而形成一个二分类训练集;这样一共产生M个训练集,可训练出M个分类器
- 解码:M个分类器分别对测试样本进行预测,这些预测标记组成了一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小额类别作为最终预测结果。
- 类别划分:通过“编码矩阵”指定,常见的主要有二元码和三元码。
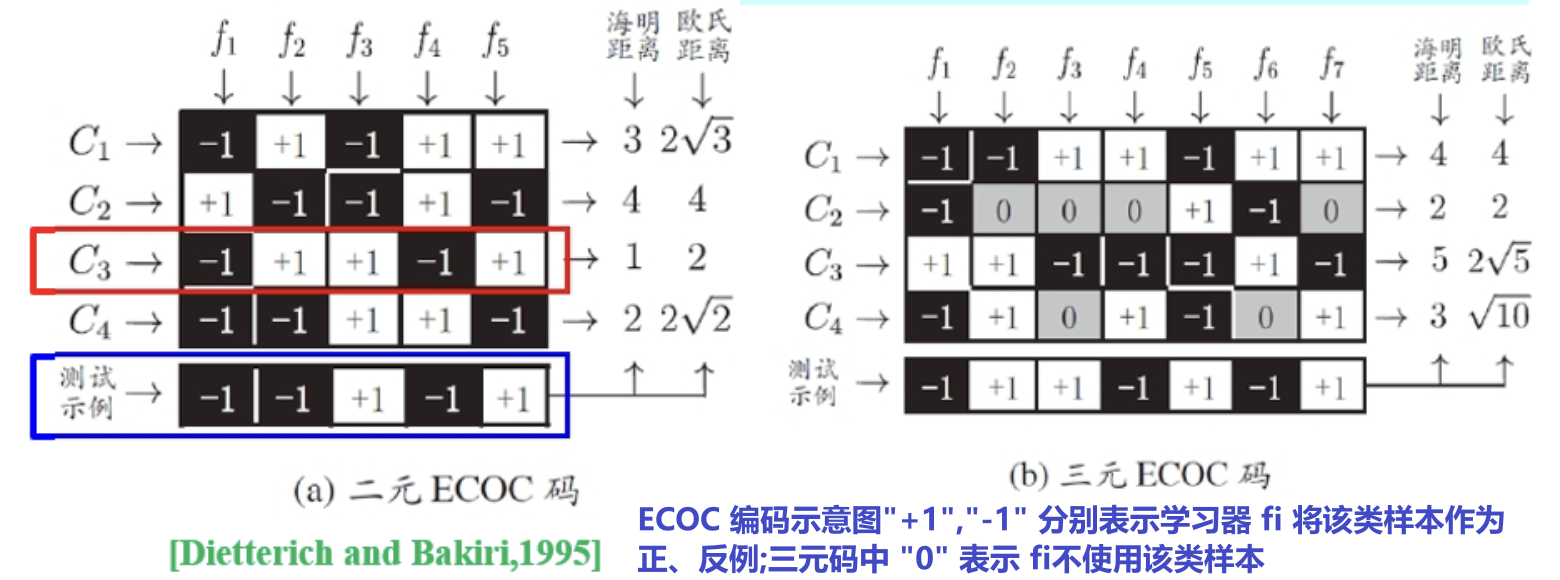
手稿阐述二元码、三元码:

3.6 类别不平衡
类别不平衡(class-imbalance)
问题描述:分类任务中不同类别的训练样例差别很大的情况。
类别不平衡的基本处理方法:
1、当正、反例可能性相同时(即阈值为0.5的情况),分类器的决策规则为:\(\frac{y}{1-y} (3.46)\)则预测为正例。
2、当训练集是样本总体的无偏采样时,m+代表正例数量,m-代表负例数量,观测几率=\(\frac{m^{+}}{m^{-}}\),分类器的决策规则为\(\frac{y}{1-y}>\frac{m^{+}}{m^{-}}(3.47)\)则预测为正例
当分类器决策时基于形式(3.46),可以通过“再缩放”策略,使其基于式(3.46)决策,实际是执行(3.47)
"再缩放":\(\frac{y^{'}}{1-y^{'}}=\frac{y}{1-y}×\frac{m^{-}}{m^{+}} (3.48)\)
3、上面假设不成立时,则无法基于训练集类别进行推断真实几率,但也有三种处理方法
- 欠采样(undersampling):去除一些反例,从而使正、反例数目接近。
- 过采样(oversampling):增加一些正例,使得正、反例数目接近
- 阈值移动(threshold-moving):直接基于原始数据集进行学习,但在训练好的分类器进行预测时,将式(3.48)嵌入到决策过程。
上篇主要介绍和讨论了线性模型。首先从最简单的最小二乘法开始,讨论输入属性有一个和多个的情形,接着通过广义线性模型延伸开来,将预测连续值的回归问题转化为分类问题,从而引入了对数几率回归,最后线性判别分析LDA将样本点进行投影,多分类问题实质上通过划分的方法转化为多个二分类问题进行求解。本篇将讨论另一种被广泛使用的分类算法--决策树(Decision Tree)。
第4章 决策树
4.1基本流程
一棵决策树包含一个根节点、若干个内部节点和若干叶节点;叶节点对应于决策结果,其他每个节点对应与一个属性测试;
决策树的目的是为了产生一棵泛化能力强,即处理未见示例能力强的决策树。
决策树的构造:
决策树的构造是一个递归的过程,有三种情形会导致递归返回:
- (1) 当前结点包含的样本全属于同一类别,这时直接将该节点标记为叶节点,并设为相应的类别;
- (2) 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分,这时将该节点标记为叶节点,并将其类别设为该节点所含样本最多的类别;
- (3) 当前结点包含的样本集合为空,不能划分,这时也将该节点标记为叶节点,并将其类别设为父节点中所含样本最多的类别。
算法的基本流程如下图所示:

可以看出:决策树学习的关键在于如何选择划分属性,不同的划分属性得出不同的分支结构,从而影响整颗决策树的性能。属性划分的目标是让各个划分出来的子节点尽可能地“纯”,即属于同一类别。因此下面便是介绍量化纯度的具体方法,决策树最常用的算法有三种:ID3,C4.5和CART。
4.2 划分选择
问题描述:如何选择最优划分属性.一般而言,随着划分过程的进行,我们希望决策树的分支节点所包含的样本尽可能属于同一类别.
1、信息增益(决策树ID3训练算法)
1、信息与熵的概念和度量
熵:一种事件的不确定性称为熵。比如刮刮乐,没刮之前不知道结果,熵最大;
信息:消除不确定性的物理量。消除方法有:调整概率、排除干扰、确定情况
噪声:不能消除某人对某事件不确定的实物
数据:噪声+信息
2、信息熵(information entropy)如何度量?
等概率分布:\(n=log_{2}^{m}\)
8个等概率的不确定情况,相当于抛3个硬币,熵为3bit
4个等概率的不确定情况,相当于抛2个硬币,熵为2bit
假设有m种等概率的不同情况,m=2^k,那么\(n=log_{2}^m=k(bit)\)
非等概率分布(一般分布):\(Ent(D)=-\sum_{k=1}^{|y|}p_{k}log_{2}^{p_{k}},其中|y|表示类别数\)
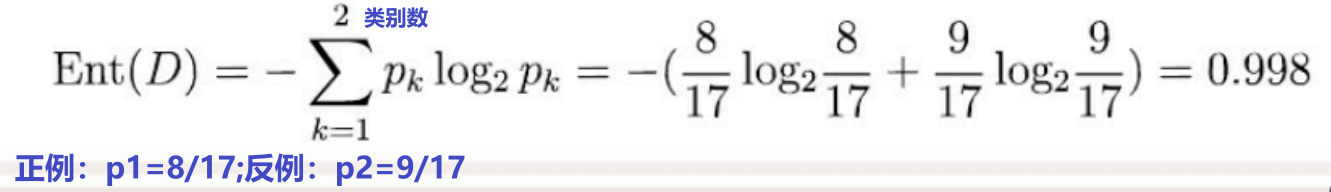
3、信息如何量化?
得知信息前后,熵的差额,就是信息的量。
比如:ABCD 四个选项,一开始的熵为2bit,当得知C有一半正确时,A(1/6),B(1/6),C(1/2),D(1/6) 此时的熵为:1.79,则信息为0.21bit
4、信息增益
信息增益表示了属性a对样本集D划分所获得的纯度越大(尽可能归属同一类别)。ID3决策树算法就是以信息增益为准则来选择划分属性。
5、西瓜数据集2.0案例,演示ID3算法
步骤:

2、增益率(C4.5算法)
信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的C4.5决策树算法不直接使用信息增益,而是使用 “增益率”来选择最优划分属性。
属性a的可能取值数目越多(即V越大),则IV(a)的值通常会越大。
增益率准则对可取值数较少的属性有所偏好,因此C4.5并不是选择增益率最大的候选划分属性,而是使用一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
3、基尼指数(CART算法)
CART算法使用"基尼指数"(Gini index)来选择划分属性。数据集D的纯度用基尼值来度量:
直观来说,Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率.因此Gini(D)越小,则数据集D的纯度越高。
属性a的基尼指数:
于是,我们在候选属性集合A中,选择哪个使得划分后基尼指数最小的属性作为最优划分属性,\(a_{*}=arg_{a\in A}\space min\space Gini\_index(D,a)\)
CART算法回归树,待定
4.3 剪枝处理
目的:防止过拟合
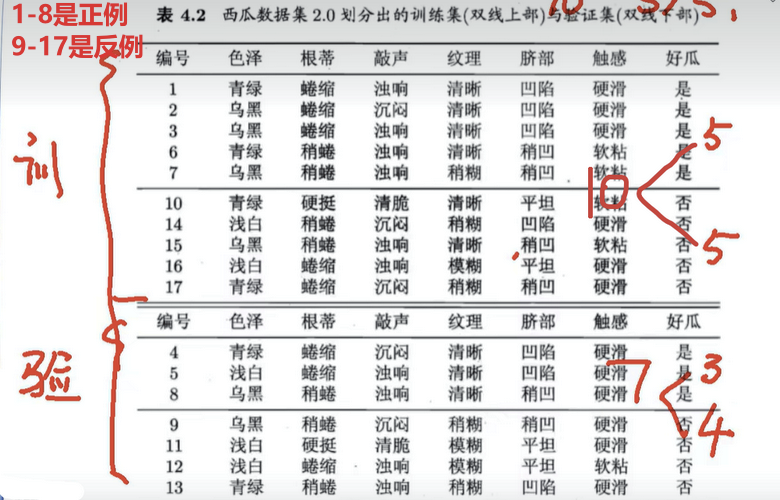
基于信息增益准则生成的决策树:
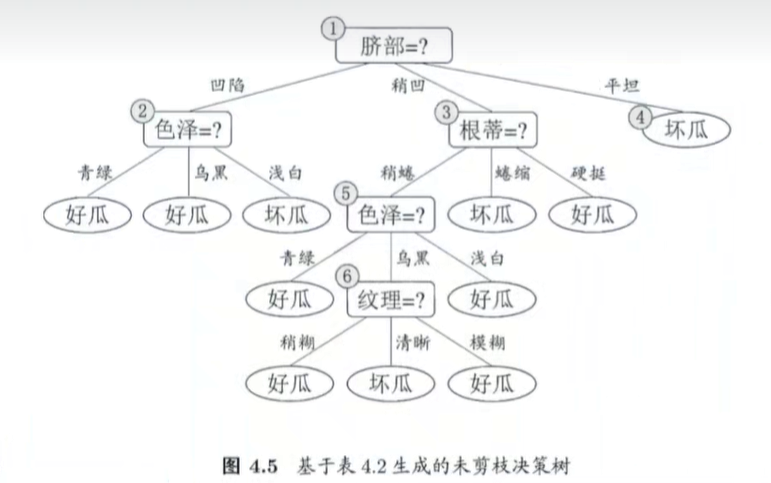
训练集与验证集在决策树上的情况
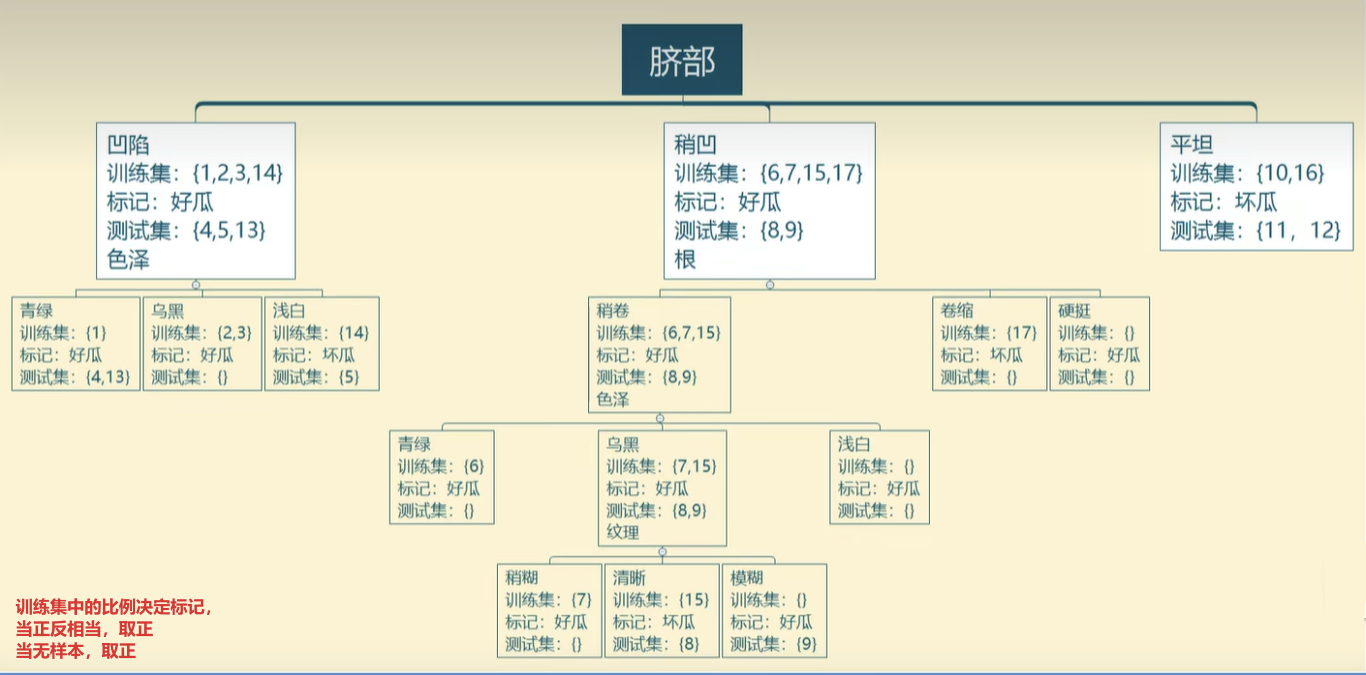
1、预剪枝
自上而下,能减则减

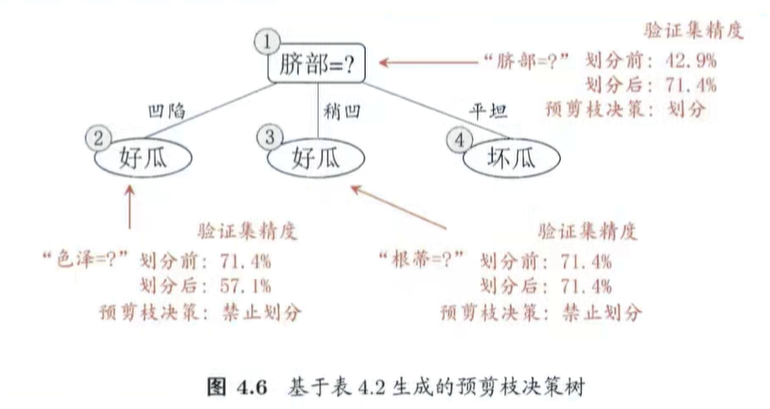
预剪枝分析:
2、后剪枝
自下而上,能不减则不减
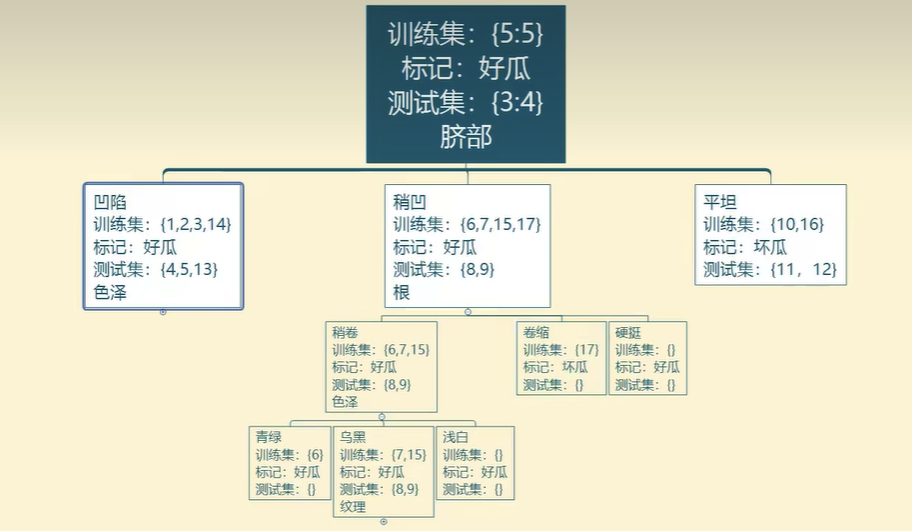
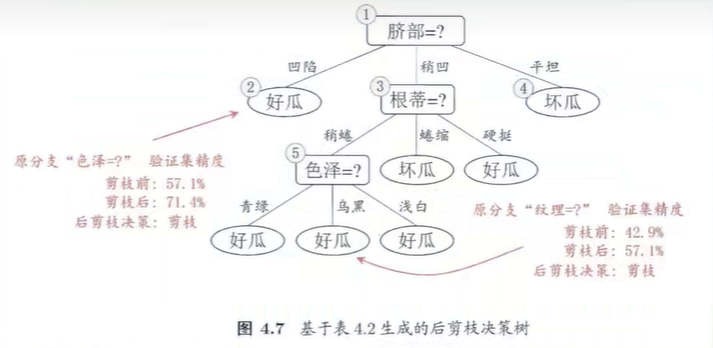
3、对剪枝细节的补充
1、每次计算验证集精度时,是考虑了所有验证集的样本,不是某一分支下的样本数。
4.4连续与缺失值
1、连续值处理
C4.5算法下有:二分法
属性a的取值连续,比如从1到100,并分成\(a_{1},a_{2},a_{3},a_{4}\)
根据二分法,则取\(t=\frac{a_{i}+a{j}}{2},i与j相邻\),故此时的信息增益表示为:
2、缺失值处理
C4.5例子




注:
1、思绪梳理:按去除缺失值的样本计算信息增益,再对信息增益放大到整个样本进行权重处理。
2、\(\frac{14}{17}\)有两种解释:1、对缺失值的惩罚;2、样本数减少,信息增益也减少
其他方法:
离散值:众数填充;相关性最高的列填充
连续值:中位数;相关性最高的列做线性回归进行估计
4.5多变量决策树
普通决策树
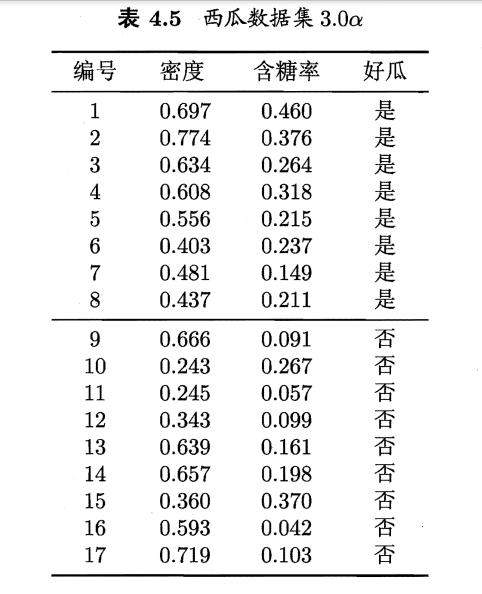
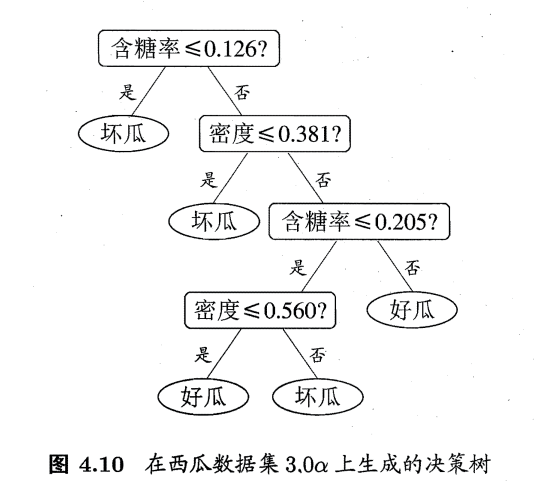
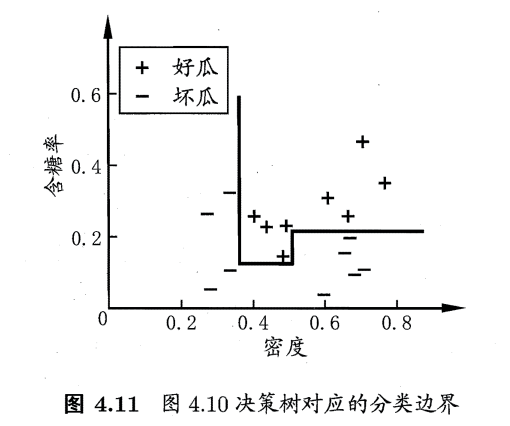
普通决策树的特点:形成的分类边界有一个明显的特点:轴平行(axis- parallel) ,即它的分类边界由若干个与坐标轴平行的分段组成.
然而真实分类边界比较复杂。"多变量决策树"可以实现斜划分
多变量决策树
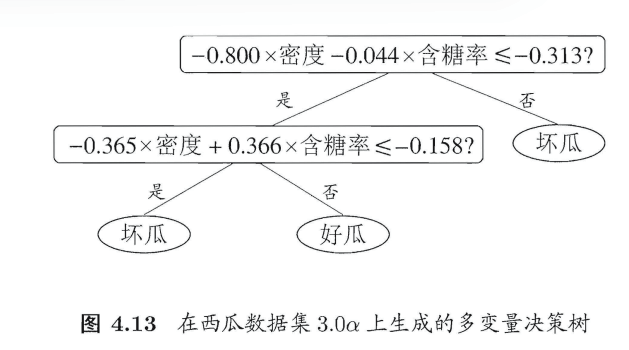
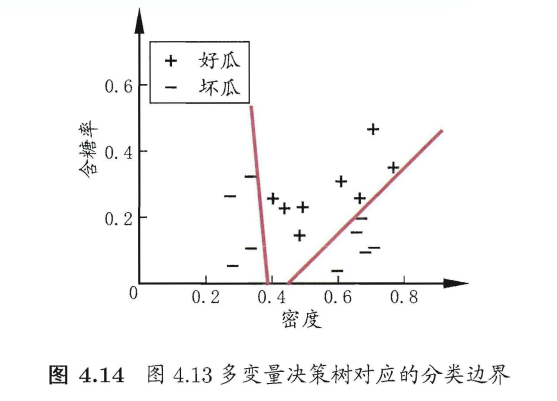
在多变量决策树的学习过程中,不是为每个非叶结点寻找一个最优划分属性,而是试图建立一个合适的线性分类器。
4.6阅读资料
决策树有很多算法:
ID3 ; C4.5 ; CART ; C4.5Relu ; 多变量决策树算法OC1(贪心寻找每个属性的最优权值;线性分类器最小二乘法) ;感知机树(决策树的叶节点上嵌入神经网络);
泛化能力影响:
剪枝方法:有实验研究表明,在数据具有噪声的情况下,通过剪枝可提高25%的性能
参考资料
- 知乎:决策数算法的Python实现-黄耀鹏
- youtube:StatQuest
- hands on machine learning 2nd
- 西瓜书
- 知乎:Yjango视频
- A Mathematical Theory of Communication By C.E.SHANNON 1948

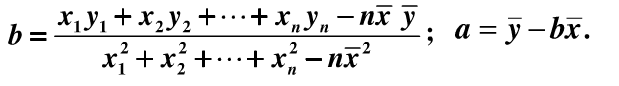

 浙公网安备 33010602011771号
浙公网安备 33010602011771号