数理统计

第2章 数理统计的基本概念

在概率论中，所研究的随机变量，它的分布都是假设已知的。
在数理统计中，所研究的随机变量，它的分布是未知的。

 

2.1 简单随机样本

数理统计的核心问题：由样本推断总体

为了了解总体X的分布规律或某些特征，往往通过从总体中抽取一部分个体，根据从这些个体获得的数据来对总体的分布做出推断，

 

2.1.1总体与个体

总体：研究对象的全体
样本：总体中抽取的一部分个体。
样本容量：样本中所含个体的数量。
抽样：从总体中抽取若干个体的过程。其目的是为了获取样本以推断总体的性质。
 

2.1.2简单随机样本

样本的二重性：样本要能很好的反映总体的特征，因此需要具有如下性质。

1. 同分布性：要求样本\(X_{1},X_{2},X_{3},...,X_{n}\)同分布且与总体\(X\)具有相同的分布。
2. 独立性：要求样本\(X_{1},X_{2},X_{3},...,X_{n}\)相互独立

设\(X_{1},X_{2},X_{3},...,X_{n}\)是来自总体\(X\)的容量为n的样本.由于\(X_{1},X_{2},X_{3},...,X_{n}\)都是从总体\(X\)中随机抽取的，它的取值就在总体\(X\)的可能取值范围内随机取得，自然\(X_{1},X_{2},X_{3},...,X_{n}\)也是随机变量

定义1. 设\(X\)是具有分布函数\(F\)的随机变量，若\(X_{1},X_{2},X_{3},...,X_{n}\)是具有同一分布函数\(F\)的、相互独立的随机变量，则称\(X_{1},X_{2},X_{3},...,X_{n}\)为从分布函数\(F\)(或总体\(F\)、或总体\(X\))得到的容量为\(n\)的简单随机样本，简称样本，它们的观察值\(x_{1},x_{2},x_{3},...,x_{n}\)，称为样本观察值。
 

样本可以看成一个随机向量，写成\((X_{1},X_{2},X_{3},...,X_{n})\)，此时样本值相应地写成\((x_{1},x_{2},x_{3},...,x_{n})\).
若\((x_{1},x_{2},x_{3},...,x_{n})\)与\((y_{1},y_{2},y_{3},...,y_{n})\)都是对应于样本\((X_{1},X_{2},X_{3},...,X_{n})\)的样本值，一般来说它们是不相同的。

 

关于样本的分布有如下结论：
 设总体\(X\)的分布函数\(F(x)\)，则样本\(X_{1},X_{2},X_{3},...,X_{n}\)的联合分布函数为

\[ F(x_{1},x_{2},...,x_{n})=\prod_{i=1}^{n}F(x_{i}) \]

  若总体\(X\)是离散型随机变量，其分布律为\(P\{{X=x_{i}}\}=p(x_{i})(i=1,2,...)\)，则样本\(X_{1},X_{2},X_{3},...,X_{n}\)的联合分布律为：

\[ P\{{X_{1}=x_{1},X_{2}=x_{2},..,X_{n}=x_{n}}\}=\prod_{i=1}^{n}p(x_{i}) \]

 若总体\(X\)是连续型随机变量，其概率密度函数为\(f(x)\)，则样本\(X_{1},X_{2},X_{3},...,X_{n}\)的联合概率密度函数为：

\[ f(x_{1},x_{2},..,x_{n})=\prod_{i=1}^{n}f(x_{i}) \]

2.1.3常用统计量

定义2：设\(X_{1},X_{2},X_{3},...,X_{n}\)是来自总体\(X\)的一个样本，若样本函数\(g(X_{1},X_{2},X_{3},...,X_{n})\)中不含有任何未知参数，则称\(g(X_{1},X_{2},X_{3},...,X_{n})\)为统计量.
 例如:若

因为\(X_{1},X_{2},X_{3},...,X_{n}\)都是随机变量，而统计量 \(g(X_{1},X_{2},X_{3},...,X_{n})\)是随机变量的函数，因此统计量也是一个随机变量.设\((x_{1},x_{2},..,x_{n})\)是相应于样本\(X_{1},X_{2},..,X_{n}\)的样本值，则称\(g(x_{1},x_{2},x_{3},...,x_{n})\)是\(g(X_{1},X_{2},X_{3},...,X_{n})\)的观察值。

设\(X_{1},X_{2},X_{3},...,X_{n}\)是来自总体\(X\)的样本，\(x_{1},x_{2},x_{3},...,x_{n}\)为样本观察值，常用的统计量有：
1、样本均值为：

\[ \overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i} \]

 其观察值为：

\[ \overline{x}=\frac{1}{n}\sum_{i=1}^{n}x_{i} \]

2.样本方差：

\[ S^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}=\frac{1}{n-1}(\sum_{i=1}^{n}X_{i}^{2}-n\overline{X}^{2}) \]

 其观察值为：

\[ s^{2}=\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}=\frac{1}{n-1}(\sum_{i=1}^{n}x_{i}^{2}-n\overline{x}^{2}) \]

  在参数估计中还有统计量\(S_{n}^{2}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}\),称为未修正的样本方差。
  两者间关系：

\[ S^{2}=\frac{n}{n-1}S_{n}^{2} \]

3.样本标准差

\[ S=\sqrt{S^{2}}=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \]

 其观察值：

\[ s=\sqrt{s^{2}}=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}} \]

4.样本k阶(原点)矩为

\[ A_{k}=\frac{1}{n}\sum_{i=1}^{n}X_{i}^{k}\space,k=1,2,.... \]

 其观察值：

\[ a_{k}=\frac{1}{n}\sum_{i=1}^{n}x_{i}^{k}\space,k=1,2,.... \]

5.样本k阶中心矩为

\[ B_{k}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\overline{X})^{k}\space,k=1,2,... \]

 其观察值：

\[ b_{k}=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\overline{x})^{k}\space,k=1,2,... \]

上述统计量统称为样本的矩统计量，简称样本矩。显然，样本均值\(\overline{X}\)为样本一阶原点矩\(A_{1}\),未修正的样本方差\(S_{n}^{2}\)为样本二阶中心矩\(B_{2}\)

 
关于样本的k阶矩，有下述结论：
定理1：

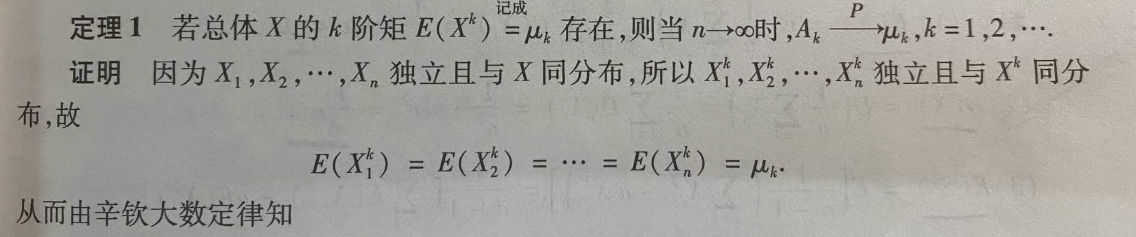
6.顺序统计量：设\(X_{1},X_{2},...,X_{n}\)是来自总体X的样本,将样本中的各分量按其观察值由小到大的顺序排列成

\[X_{(1)}\leq X_{(2)}\leq...\leq X_{(n)} \]

则称\(X_{(1)},X_{(2)},...,X_{(n)}\)为顺序统计量,\(X_{(i)}\)为第i个顺序统计量,其中\(X_{(1)}\)和\(X_{(n)}\)称为最小和最大统计量,即
\(X_{(1)}= min\{X_{1},X_{2},...,X_{n}\},X_{(n)}= max\{X_{1},X_{2},...,X_{n}\}\)

7.样本中位数:设\(X_{1},X_{2},...,X_{n}\)是来自总体的样本,\(X_{(1)},X_{(2)},...,X_{(n)}\)是其统计量,则

\[ \tilde{X}= \begin{cases} X_{(\frac{n+1}{2})},n为奇数\\ \frac{1}{2}[X_{(\frac{n}{2})}+X_{(\frac{n}{2}+1)}]，n为偶数 \end{cases} \]

 其观察值：

\[ \tilde{x}= \begin{cases} x_{(\frac{n+1}{2})},n为奇数\\ \frac{1}{2}[x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)}]，n为偶数 \end{cases} \]

 由定义可知,当n为奇数时,样本中位数取\(X_{(1)},X_{(2)},...,X_{(n)}\)的正中间那个数;当n为偶数时,样本中位数取正中间两个数的算术平均值.例如数据 8,1,3 的中位数是3;数据8,1,3,1的中位数是2.

8.样本众数:设\(X_{1},X_{2},...,X_{n}\)是来自总体的样本,样本\(X_{1},X_{2},...,X_{n}\)的n个观察值中出现次数最多的数值,称为样本众数,记为\(\hat{X}\).
 众数是随机变量取值可能性最大的那个值,是反映随机变量取值位置的量.一组数据中的众数不一定只有一个,可能有两个或两个以上.例如数据 1,2,3,3,4的众数是3;数据1,2,2,3,3,4 的众数是2和3.

 例2-3 如果总体X有有限的\(数学期望 E(X)=μ，方差D(X)=\sigma^{2}\)，\(X_{1},X_{2},...,X_{n}\)是来自了的一个样本,\(\overline{X},S^{2}\)分别是样本均值与样本方差,证明:\((1)E(\overline{X})=μ; (2)D(\overline{X})=\sigma^{2}/n; (3)E(S^{2}) =\sigma^{2}.\)

解:

\[ (1)\space E(\overline{X})=E(\frac{1}{n}\sum_{i=1}^{n}X_{i})=\frac{1}{n}\sum_{i=1}^{n}E(X_{i})=\frac{1}{n}·nμ=μ\\ (2)\space D(\overline{X})=D(\frac{1}{n}\sum_{i=1}^{n}X_{i})=\frac{1}{n^{2}}\sum_{i=1}^{n}D(X_{i})=\frac{1}{n^{2}}·n\sigma^{2}=\frac{\sigma^{2}}{n}\\ (3)\space E(S^{2})=E[\frac{1}{n-1}(\sum_{i=1}^{n}X_{i}^{2}-n\overline{X}^{2})]=\frac{1}{n-1}[\sum_{i=1}^{n}E(X_{i}^{2})-nE(\overline{X}^{2})]=\frac{1}{n-1}[\sum_{i=1}^{n}(\sigma^{2}+μ^{2})-n(\frac{\sigma^{2}}{n}+μ^{2})]=\sigma^{2} \]

注意：这三个结果应记住，在构造统计量时经常用到。

第3章参数估计

研究对象：1、总体X，分布未知；2、分布形式已知，但含未知参数；
研究方法:总体--(抽样)-->样本X1,X2,..,XN ->统计量g(X1,X2,...,XN)

引例：

3.1 点估计