卷积的介绍

先看到卷积运算，知道了卷积就是把模版与图像对应点相乘再相加，把最后的结果代替模版中心点的值的一种运算。但是，近来又看到了积分图像的定义，立马晕菜，于是整理一番，追根溯源一下吧。

1 卷积图像

1.1 源头

首先找到了一篇讲解特别好的博文，原文为：卷积

贴过正文来看：

---------------------------------------------------------------------------------------------------------------

信号处理中的一个重要运算是卷积.初学卷积的时候,往往是在连续的情形, 
　　两个函数f(x),g(x)的卷积,是∫f(u)g(x-u)du 
　　当然，证明卷积的一些性质并不困难，比如交换，结合等等，但是对于卷积运算的来处，初学者就不甚了了。 
　　 
　　其实，从离散的情形看卷积，或许更加清楚， 
　　对于两个序列f[n],g[n],一般可以将其卷积定义为s[x]= ∑f[k]g[x-k] 
　　 
　　卷积的一个典型例子,其实就是初中就学过的多项式相乘的运算, 
　　比如(x*x+3*x+2)(2*x+5) 
　　一般计算顺序是这样, 
　　(x*x+3*x+2)(2*x+5) 
　　= (x*x+3*x+2)*2*x+(x*x+3*x+2)*5 
　　= 2*x*x*x+3*2*x*x+2*2*x+ 5*x*x+3*5*x+10 
　　然后合并同类项的系数, 
　　2 x*x*x 
　　3*2+1*5 x*x 
　　2*2+3*5 x 
　　2*5 
　　---------- 
　　2*x*x*x+11*x*x+19*x+10 
　　 
　　实际上,从线性代数可以知道,多项式构成一个向量空间,其基底可选为 
　　{1,x,x*x,x*x*x,...} 
　　如此,则任何多项式均可与无穷维空间中的一个坐标向量相对应, 
　　如,(x*x+3*x+2)对应于 
　　(1 3 2), 
　　(2*x+5)对应于 
　　(2,5). 
　　 
　　线性空间中没有定义两个向量间的卷积运算,而只有加法,数乘两种运算,而实际上,多项式的乘法,就无法在线性空间中说明.可见线性空间的理论多么局限了. 
　　但如果按照我们上面对向量卷积的定义来处理坐标向量, 
　　(1 3 2)*(2 5) 
　　则有 
　　2 3 1 
　　_ _ 2 5 
　　-------- 
　　    2 
　　 
　　 
　　2 3 1 
　　_ 2 5 
　　----- 
　　  6+5=11 
　　 
　　2 3 1 
　　2 5 
　　----- 
　　4+15 =19 
　　 
　　 
　　_ 2 3 1 
　　2 5 
　　------- 
　　  10 
　　 
　　 或者说, 
　　(1 3 2)*(2 5)=(2 11 19 10) 
　　 
　　回到多项式的表示上来, 
　　(x*x+3*x+2)(2*x+5)= 2*x*x*x+11*x*x+19*x+10 
　　 
　　似乎很神奇,结果跟我们用传统办法得到的是完全一样的. 
　　换句话,多项式相乘,相当于系数向量的卷积. 
　　 
　　其实,琢磨一下,道理也很简单, 
　　卷积运算实际上是分别求 x*x*x ,x*x,x,1的系数，也就是说，他把加法和求和杂合在一起做了。(传统的办法是先做乘法，然后在合并同类项的时候才作加法) 
　　以x*x的系数为例，得到x*x，或者是用x*x乘5，或者是用3x乘2x,也就是 
　　2 3 1 
　　_ 2 5 
　　----- 
　　 6+5=11 
　　其实,这正是向量的内积.如此则,卷积运算,可以看作是一串内积运算.既然是一串内积运算，则我们可以试图用矩阵表示上述过程。 
　　 
　　[ 2 3 1 0 0 0] 
　　[ 0 2 3 1 0 0]==A 
　　[ 0 0 2 3 1 0] 
　　[ 0 0 0 2 3 1] 
　　 
　　[0 0 2 5 0 0]' == x 
　　 
　　b= Ax=[ 2 11 19 10]' 
　　 
　　采用行的观点看Ax,则b的每行都是一个内积。 
　　A的每一行都是序列[2 3 1]的一个移动位置。 
　　 
　　--------- 
　　 
　　显然,在这个特定的背景下,我们知道,卷积满足交换,结合等定律,因为,众所周知的,多项式的乘法满足交换律,结合律.在一般情形下,其实也成立. 
　　 
　　在这里,我们发现多项式,除了构成特定的线性空间外,基与基之间还存在某种特殊的联系,正是这种联系,给予多项式空间以特殊的性质. 
　　 
　　在学向量的时候，一般都会举这个例子，甲有三个苹果，5个橘子，乙有5个苹果，三个橘子，则共有几个苹果，橘子。老师反复告诫，橘子就是橘子，苹果就是苹果，可不能混在一起。所以有(3,5)+(5,3)=(8,8).是的，橘子和苹果无论怎么加，都不会出什么问题的，但是，如果考虑橘子乘橘子，或者橘子乘苹果，这问题就不大容易说清了。 
　　 
　　又如复数,如果仅仅定义复数为数对（a,b),仅仅在线性空间的层面看待C2,那就未免太简单了。实际上，只要加上一条(a,b)*(c,d)=(ac-bd,ad+bc) 
　　则情况马上改观，复变函数的内容多么丰富多彩，是众所周知的。 
　　 
　　另外，回想信号处理里面的一条基本定理,频率域的乘积,相当于时域或空域信号的卷积.恰好跟这里的情形完全对等.这后面存在什么样的隐态联系,需要继续参详. 
　　 
　　从这里看,高等的卷积运算其实不过是一种初等的运算的抽象而已.中学学过的数学里面，其实还蕴涵着许多高深的内容（比如交换代数）。温故而知新,斯言不谬. 
　　 
　　其实这道理一点也不复杂，人类繁衍了多少万年了，但过去n多年，人们只知道男女媾精，乃能繁衍后代。精子，卵子的发现，生殖机制的研究，也就是最近多少年的事情。 
　　 
　　孔子说，道在人伦日用中，看来我们应该多用审视的眼光看待周围，乃至自身，才能知其然，而知其所以然。

---------------------------------------------------------------------------------------------------------------

从上文我们得知了卷积的来源。我们再找一下卷积的官方定义：数学中关于两个函数的一种无穷积分运算。对于函数f1(t)和f2(t)，其卷积表示为：式中：“*”为卷积运算符号。

在泛函分析中，卷积(卷积)、旋积或摺积(英语：Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子，表徵函数f 与经过翻转和平移与g 的重叠部分的累积。函数f与g的卷积记作f(t)*g(t)，它是其中一个函数翻转并平移后与另一个函数的乘积的积分，是一个对平移量的函数。 

 函数f与g的卷积可以定义为： z(t)=f(t)*g(t)= ∫f(m)g(t-m)dm.

并且卷积定理指出：二个二维连续函数在空间域中的卷积可求其相应的二个傅立叶变换乘积的反变换而得。反之，在频域中的卷积可用的在空间域中乘积的傅立叶变换而得。

其实，说了这么多，我还是不太明白为什么要对图像进行卷积，怎样进行卷积。

1.2 卷积运算

提到卷积运算，首先离不开的就是卷积核，这个卷积核其实就是一个大小固定、由数值参数构成的数组，数组的参考点通常位于数组的中心，数组的大小称为核支撑。单就技术而言，核支撑实际上仅仅由核数组的非0部分组成。或者，像其他说法，卷积核就是所谓的模板。

卷积运算，其实就是可看作是加权求和的过程，使用到的图像区域中的每个像素分别与卷积核(权矩阵)的每个元素对应相乘，所有乘积之和作为区域中心像素的新值。
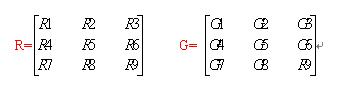
卷积示例：

  3 * 3 的像素区域R与卷积核G的卷积运算：
              R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
            

如果对一幅图像进行卷积运算，可利用以数组为中心为参考点的3*3卷积核。首先将核的参考点定位于图像的第一个像素点，核的其余元素覆盖图像总其对应的局部像素点。对于每一个核点，我们可以得到这个点的值以及图像中对应图像点的值。将这些值相乘并求和，并将这个结果放在与输入图像参考点所对应的位置。通过在整个图像上扫描卷积核，对图像的每个点重复此操作。最终可以得到图像的卷积图像。

当然，我们可以利用方程表示这个过程，定义图像为I(x,y),核为G（i,y）(其中0<i<Mi-1,0<j<Mj-1) 参考点位于（ai,aj）坐标上，则卷积H(x,y)定义如下：

H(x,y) = sum[ I(x+i-ai,y+j-aj)G(i,j)].

.常用模板（卷积核）

连续空间的卷积定义是 f(x)与g(x)的卷积是 f(t-x)g(x) 在t从负无穷到正无穷的积分值.t-x要在f(x)定义域内,所以看上去很大的积分实际上还是在一定范围的.
实际的过程就是f(x) 先做一个Y轴的反转,然后再沿X轴平移t就是f(t-x),然后再把g(x)拿来,两者乘积的值再积分.想象一下如果g(x)或者f(x)是个单位的阶越函数. 那么就是f(t-x)与g(x)相交部分的面积.这就是卷积了.
把积分符号换成求和就是离散空间的卷积定义了.

1.3 意义

卷积是各种图像变换的基础，一个特殊卷积所实现的功能是由其卷积核（模板）的形式决定的。高斯变换就是用高斯函数对图像进行卷积。

平滑处理：平滑类型：简单模糊（对邻域求和，并缩放），简单无缩放变换的模糊（对邻域求和），中值模糊（中值滤波），高斯模糊（高斯卷积），双边模糊（双线性滤波）。

膨胀和腐蚀。

图像金字塔

拉普拉斯变换、canny算子（求导数）

卷积性质：

1.卷积的符号表示式表明卷积是一种特殊类型的乘法，乘法某些代数性质可用于卷积。

    (1)commutative law：f₁(t)*f₂(t)=f₂(t)*f₁(t)
    (2)distributive law：f₁(t)*[f₂(t)+f₃(t)]=f₁(t)*f₂(t)+f₁(t)*f₃(t)
    (3)associative law：[f₁(t)*f₂(t)]*f₃(t)=f₁(t)*[f₂(t)*f₃(t)]
    (4)shift invariace：若f₁(t)*f₂(t)=f₃(t)，则f₁(t-t₀)*f₂(t)=f₁(t)*f₂(t-t₀)=f₃(t-t₀)
    此性质表明无论哪个函数平移了一个距离t₀,则所得的卷积就是简单平移了同一距离，但大小和形状保持不变。

2.卷积的微分和积分

    (1)两函数相卷积后的导数等于两函数之一的导数与另一函数相卷积。

    (2)两函数相卷积后的积分等于两函数之一的积分与另一函数相卷积。

    (3)推广

    若f1(t)*f2(t) = s(t), 则，两个分别为m阶和n阶函数导数卷积，由它们卷积的（m+n)阶导数给出。

3.奇异信号的卷积特性：

    (1)f(t)*δ(t)=f(t)    f(t)*δ(t-t₀)=f(t-t₀)   f(t-t₁)*δ(t-t₀)=f(t-t₀-t₁) 
    (2)δ(t)*δ(t)=δ(t)
    (3)f(t)*δ'(t)=f'(t)
    (4)
    推广：f(t)*δ^(k)(t)=f^(k)(t)    f(t)*δ^(k)(t-t₀)=f^(k)(t-t₀)
    (5)f(t)*δ'(t)*u(t)=f'(t)*u(t)=f(t)    f(t)*δ''(t)*tu(t)=f''(t)*tu(t)=f(t)

所以，图像卷积与积分图像有什么关系吗？知者告知我啊。。。。。。

2 积分图像

surf算法中要用到积分图像的概念。借助积分图像，图像与高斯二阶微分模板的滤波转化为对积分图像的加减运算。积分图像（Integral Image）的概念是由viola和Jones提出来的，而将类似积分图像用于盒子滤波是由Simard等人提出。

积分图像中任意一点（i,j）的值为ii(i,j)为原图像左上角到任意点（i,j）相应的对角线区域灰度值的总和即：

公式中，I(x`,y`)表示原图像中点（i`,j`）的灰度值，ii（x,y）可以由下面两公式迭代计算得到：

公式中，S（x,y）表示一列的积分，且S（i,-1）=0,ii(-1,j)=0.求积分图像，只需对原图像的所有像素素进行一遍扫描。下面的代码为c++语言的实现

pOutImage[0][0] = pInImage[0][0];

for(int x = 1, x < nWidth; i++)
{
  pOutImage[x][0] = pInImage[x-1][0] + pInImage[x][0];

}

for(int y=1; y< nHeight ;y++)
{
  int nSum = 0;

  for(int x=0; x < nWidth;x++)
  {
    nSum = pInImage[x][y];

    pOutImage[x][y]= pInImage[x][y-1]+nSum;
  }

}

如图表示，在求取窗口w内的像元灰度和时，不管窗口W的大小如何，均可利用积分图像的4个对应点（i1,j1）（i2,j2）（i3,j3）（i4,j4）的值计算的到。也就是说，求取窗口W内的像元灰度和与窗口的尺寸是无关的。窗口W内的像元的灰度和为

Sum（W）= ii(i4,j4) -ii(i2,j2) - ii(i3,j3) + ii(i1,j1)

下面看以截图，相信都可以看懂

关于矩形区域内像素点的求和应该是一种简单重复性运算，采用这种思路总体上提高了效率。为什么这么说呢？假设一幅图片共有n个像素点，则计算n个位置的积分图总共的加法运算有n-1次（注意：可不是次哦，要充分利用递推思想），将这些结果保存在一个跟原图对应的矩阵M中。当需要计算图像中某个矩形区域内的所有像素之和是直接像查表一样，调出A,B,C,D四点的积分图值，简单的加减法（注意只需要三次哦）即可得到结果。反之，如果采用naive的方式直接在原图像中的某个矩形区域内求和，你想想，总共可能的矩形组合有多少？ ！！且对于一幅图像n那是相当大啊，所以2^n

 那可是天文数字，而且这里面绝大部分的矩形有重叠，重叠意味着什么？在算求和的时候有重复性的工作，其实我们是可以有效的利用已经计算过的信息的。这就是积分图法的内在思想：它实际上是先计算n个互不重叠（专业点说是不相交）的矩形区域内的像素点求和，充分利用这些值（已有值）计算未知值，有点类似递推的味道...这就完全避免了重复求和运算。

 这样就可以进行2种运算：

    （1）任意矩形区域内像素积分。由图像的积分图可方便快速地计算图像中任意矩形内所有像素灰度积分。如下图2.3所示，点1的积分图像ii1的值为(其中Sum为求和) :

    ii1=Sum（A）

   

 

    同理，点2、点3、点4的积分图像分别为：

    ii2=Sum(A)+Sum(B);      ii3=Sum(A)+Sum(C);    ii4=Sum(A)+Sum(B)+Sum(C)+Sum(D);

    矩形区域D内的所有像素灰度积分可由矩形端点的积分图像值得到:

                   Sum(D)=ii1+ii4-(ii2+ii3)            (1)

(2) 特征值计算
    矩形特征的特征值是两个不同的矩形区域像素和之差，由(1)式可以计算任意矩形特征的特征值，下面以图2.1中特征原型A为例说明特征值的计算。

    

    如图2.4 所示，该特征原型的特征值定义为:

 

    Sum（A）-Sum（B）

 

    根据（1）式则有：Sum(A)=ii4+ii1-(ii2+ii3);    Sum(B)=ii6+ii3-(ii4+ii5);

 

   所以此类特征原型的特征值为:

 

                (ii4-ii3)-(ii2-ii1)+(ii4-ii3)-(ii6-ii5)

 

   另示：运用积分图可以快速计算给定的矩形之所有象素值之和Sum(r)。假设r=(x,y,w,h),那么此矩形内部所有元素之和等价于下面积分图中下面这个式子:

 

                 Sum(r) = ii(x+w,y+h)+ii(x-1,y-1)-ii(x+w,y-1)-ii(x-1,y+h)

 

   由此可见，矩形特征特征值计算只与此特征端点的积分图有关，而与图像坐标值无关。对于同一类型的矩形特征，不管特征的尺度和位置如何，特征值的计算所耗费的时间都是常量，而且都只是简单的加减运算。其它类型的特征值计算方法类似。