泰勒定理
泰勒定理[编辑]
对于一般的函数,泰勒公式的系数的选择依赖于函数在一点的各阶导数值。这个想法的原由可以由微分的定义开始。微分是函数在一点附近的最佳线性近似:
![f(a + h) = f(a) + f^{\prime}(a)h + o(h)]() ,其中
,其中![o(h)]() 是比h 高阶的无穷小。
是比h 高阶的无穷小。
也就是说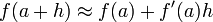 ,或
,或 。
。
注意到 和
和 在a 处的零阶导数和一阶导数都相同。对足够光滑的函数,如果一个多项式在a 处的前n 次导数值都与函数在a 处的前n 次导数值重合,那么这个多项式应该能很好地近似描述函数在a 附近的情况。以下定理说明这是正确的:
在a 处的零阶导数和一阶导数都相同。对足够光滑的函数,如果一个多项式在a 处的前n 次导数值都与函数在a 处的前n 次导数值重合,那么这个多项式应该能很好地近似描述函数在a 附近的情况。以下定理说明这是正确的:
 的表达形式有若干种,分别以不同的数学家命名。
的表达形式有若干种,分别以不同的数学家命名。
带有皮亚诺型余项的泰勒公式说明了多项式和函数的接近程度:
![f(x) = f(a) + \frac{f'(a)}{1!}(x - a) + \frac{f^{(2)}(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + o[(x - a)^{n}]](http://upload.wikimedia.org/math/7/8/d/78de334d75c5b4d5824d8b0c76a0a669.png)
也就是说,当x 无限趋近a 时,余项 将会是
将会是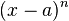 的高阶无穷小,或者说多项式和函数的误差将远小于
的高阶无穷小,或者说多项式和函数的误差将远小于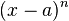 [3]。这个结论可以由下面更强的结论推出。
[3]。这个结论可以由下面更强的结论推出。
带有拉格朗日型余项的泰勒公式可以视为拉格朗日微分中值定理的推广:
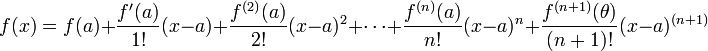
即 ,其中
,其中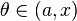 [4]。
[4]。
带有积分型余项的泰勒公式可以看做微积分基本定理的推广[5]:
余项估计[编辑]
拉格朗日型余项或积分型余项可以帮助估计泰勒展开式和函数在一定区间之内的误差。设函数在区间[a − r, a + r] 上n 次连续可微并且在区间(a − r, a + r) 上n + 1次可导。如果存在正实数Mn 使得区间(a − r, a + r) 里的任意x 都有  ,那么:
,那么:
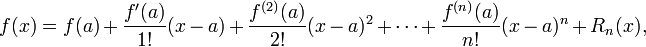
其中 。这个上界估计对区间(a − r, a + r) 里的任意x 都成立,是一个一致估计。
。这个上界估计对区间(a − r, a + r) 里的任意x 都成立,是一个一致估计。
如果当n 趋向于无穷大时,还有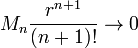 ,那么可以推出
,那么可以推出  ,f 是区间(a − r, a + r) 上解析函数。f 在区间(a − r, a + r) 上任一点的值都等于在这一点的泰勒展开式的极限。
,f 是区间(a − r, a + r) 上解析函数。f 在区间(a − r, a + r) 上任一点的值都等于在这一点的泰勒展开式的极限。
多元泰勒公式[编辑]
对于多元函数,也有类似的泰勒公式。设B(a, r ) 是欧几里得空间RN 中的开球,ƒ 是定义在B(a, r ) 的闭包上的实值函数,并在每一点都存在所有的n+1 次偏导数。这时的泰勒公式为:
- 对所有
![x\in \mathbf{B}(a, r)]() ,
, ![f(x)=\sum_{|\alpha|=0}^n\frac{1}{\alpha!}\frac{\partial^\alpha f(a)}{\partial x^\alpha}(x-a)^\alpha+\sum_{|\alpha|=n+1}R_{\alpha}(x)(x-a)^\alpha]()
其中的 α 是多重指标。
其中的余项也满足不等式:
- 对所有满足 |α| = n + 1 的 α,
![|R_{\alpha}(x)|\le\sup_{y\in\bar{B} }\left|\frac{1}{\alpha!}\frac{\partial^\alpha f(y)}{\partial x^\alpha}\right|]()
参阅[编辑]
posted on 2014-07-24 17:08 alexanderkun 阅读(3880) 评论(0) 收藏 举报

 ,其中
,其中 是比h 高阶的
是比h 高阶的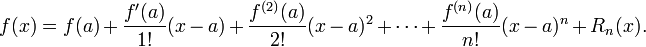
 的高阶无穷小。
的高阶无穷小。
 ,
,
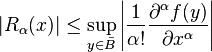


 浙公网安备 33010602011771号
浙公网安备 33010602011771号