幂级数
在数学中,幂级数是一类形式简单而应用广泛的函数级数,变量可以是一个或多个(见“多元幂级数”一节)。单变量的幂级数形式为:
其中的c和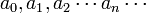 是常数。
是常数。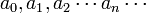 称为幂级数的系数。幂级数中的每一项都是一个幂函数,幂次为非负整数。幂级数的形式很像多项式,在很多方面有类似的性质,可以被看成是“无穷次的多项式”。
称为幂级数的系数。幂级数中的每一项都是一个幂函数,幂次为非负整数。幂级数的形式很像多项式,在很多方面有类似的性质,可以被看成是“无穷次的多项式”。
如果把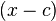 看成一项,那么幂级数可以化简为
看成一项,那么幂级数可以化简为 的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。
的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。
将一个函数写成幂级数  的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。
的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。
幂级数是分析学研究的重点之一,然而在组合数学中,幂级数也占有一席之地。作为母函数,由幂级数概念发展出来的形式幂级数是许多组合恒等式的来源[1]。在电力工程学中,幂级数则被称为Z-变换。实数的小数记法也可以被看做幂级数的一种,只不过这里的x被固定为 。在p-进数中则可以见到x被固定为
。在p-进数中则可以见到x被固定为 的幂级数。
的幂级数。
例子[编辑]
多项式可以看做系数从某一项开始全是零的幂级数,例如多项式 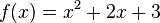 可以写成标准形式的幂级数:
可以写成标准形式的幂级数:
也可以写成(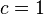 ):
):
实际上,多项式可以写成在任意c附近展开的幂级数。就这个意义上说,幂级数是多项式的推广。
等比级数的公式给出了对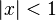 ,有
,有
![\frac{1}{1-x} = \sum_{n=0}^\infty x^n = 1 + x + x^2 + x^3 + \cdots]() ,
,
是幂级数中基本而又重要的一类。同样重要的还有指数的幂级数展开:
以及正弦函数(对所有实数x 成立):
这些幂级数都属于泰勒级数。
幂级数里不包括负的幂次。例如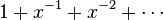 就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数
就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数 必须是和x无关,比如
必须是和x无关,比如 就不是一个幂级数。
就不是一个幂级数。
posted on 2014-07-24 16:29 alexanderkun 阅读(2648) 评论(0) 收藏 举报


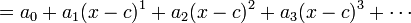


 ,
,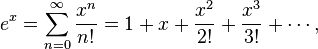



 浙公网安备 33010602011771号
浙公网安备 33010602011771号