机器学习笔记 1 LMS和梯度下降（批梯度下降） 20170617

# 概念

LMS(least mean square)：（最小均方法）通过最小化均方误差来求最佳参数的方法。

GD(gradient descent) : （梯度下降法）一种参数更新法则。可以作为LMS的参数更新方法之一。

The normal equations : （正则方程式，将在下一篇随笔中介绍）一种参数更新法则。也可以作为LMS的参数更新方法之一。

 

三者的联系和区别：LMS是一种机器学习算法。但是最小化均方误差的方法不唯一，采用GD或者正则方程式都是方法之一。 

 

# 准备样本 

必须要先理解样本集X的排布：

　　　　

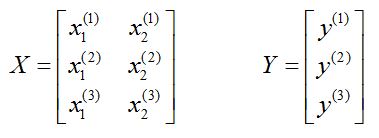
　　为了方便叙述，我们定义样本特指一个样本，样本集特指一整个样本矩阵。

　　大写 X 表示样本集矩阵。排布：一行是一个样本。

　　小写 x 表示样本集矩阵的元素。x的上标：样本序号（这个括号只是为了区别于指数，记号而已）；x的下标：样本的维度。

　　这个样本集有3个样本，每个样本2维。

　　* 样本的维度和所需要拟合的参数个数相同。（后续会说明，先不急提问）

 

　　大写Y表示所有样本的结果的集合的矩阵。

　　小写y的上标：第i个样本的结果。

　　* 样本的结果，也就是Y矩阵的元素数量和样本的数量相同.

 

　　X和Y的关系：从一个样本来看，一个样本（2维度）通过映射得到y。

 

　　LMS的目的：通过假设这种映射关系为如下，估计出最匹配的参数theta。至于该怎么更新参数，就是GD和正则方程的任务了。

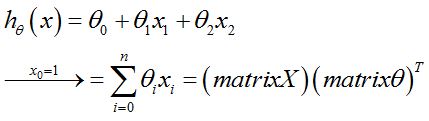
　　　　式中的h就是样本估计值（y是样本的实际值）；matrixθ是参数θ组成的列矩阵；matrixX是样本按列排的矩阵，亦即以上的大写X。

　　　　没有和吴恩达大神的讲义一致，但是我觉的h的公式应该是没问题的，mX是行，mθ是行。这点欢迎大家讨论，我也有点困惑。

　　使用 n 表示样本的维度

　　使用 m 表示样本的数量

 

 

# 数学说明

LMS表示：最小化均方误差求参数的方法，首先要给出均方误差的定义

1. 均方误差

 

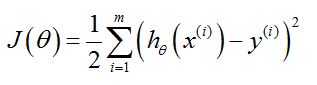
参数说明：

 　　m 是样本的数量

　　i 是样本的数量，样本总数是m，参见样本X的说明

　　J  是cost function ，损失函数。J的形式就是“均方”。

　　h 就是估计的映射关系（但是自变量其实是一个行矩阵），自变量x加上标：表示的是第i个样本，行矩阵输入到h中。h(x)得到是一个值。

　　y 加上标：表示第i个样本的实际输出值

 

LMS的目的：就是找到使得J最小的参数θ（矩阵），认为这就是h的最优参数，此时的h最接近样本的真实输出y。

问题转化为：求最小化J的参数θ（矩阵），θ的最优解问题。

方法之一：梯度下降。实际上是：在每次迭代中，提出了一种θ的更新法则

 

2. 梯度下降的应用

　　梯度下降的表达式：

 

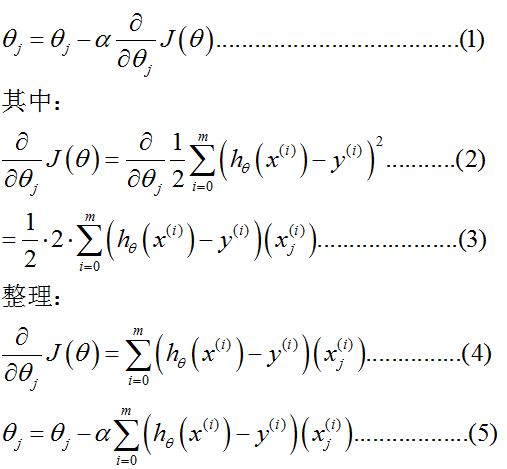
头晕了，来，解释一下。

 （1）是梯度下降的定义式，其中α表示学习率，根据经验设置（后面的例子中，设置为0.01）。θ这里是矩阵，带下标的是θ内的元素，可参看（2）。

 （2）是梯度的计算过程。将J的定义代入，m表示样本数量。下标 j 表示的是维度的序号，这里表示的是参数的序号。参数的序号和维度序号，这里讲解一下：

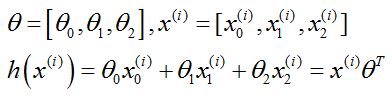
　　注意，这里样本增加了一维x0，原因参见#样本准备

　　为了满足h的形式，所以我们设置参数θ的矩阵为[θ0,θ1,θ2]。

　　这里x的上标是为了强调这是第i个样本。x的下标是维度。

　　参数的数量和样本维度一致，这样看起来就显然啦。

 

　　这里就注意到了，式中 x上标i 就是矩阵，θ这里也是矩阵。

 

　　这里也没有吴恩达大神的讲义一致。

 

（3）计算偏微分，求和号要是不理解，写两项算一下就知道了。y上标i 是数值，对θ下标j求导为零。h对θ下标j求导得x下标j上标i。

（4）（5）就是最后的结果，其中（5）是每项θ下标j的更新法则。

 数学推导的（5）一般不直接拿来写成代码，因为代码实现上，矩阵形式更有优势。

 

3. 梯度下降的矩阵表达式

 

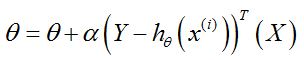
　　其中：θ和 x上标i 是矩阵，定义参见2（2）；X和Y也是矩阵，参见#准备样本；

　　矩阵形式的好处是，求和过程被简单的表达（行矩阵*列矩阵=值），代码实现就方便了。

　　每次迭代，自变量就是第i个样本（x上标i），因变量就是参数矩阵（θ）。

　　

至此，就可以准备开始写代码了。

 

# matlab例程

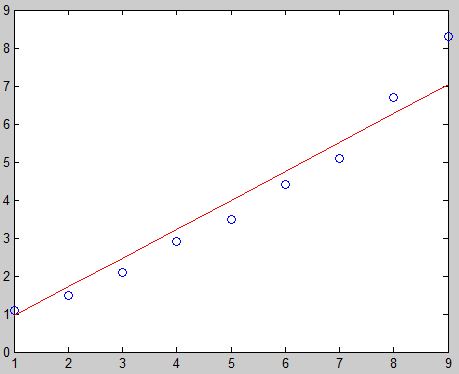
function LMS_GD()
% 参数准备 m表示矩阵
% mX每行是一个样本，样本按照列排列
% mY是每个样本的输出值，按列排列
% mTheta是参数矩阵，按照行排列，参数数量=样本维度
% alpha是学习率
mX = [1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9]; 
mY = [1.1; 1.5; 2.1; 2.9; 3.5; 4.4; 5.1; 6.7; 8.3];
mThetas = [0.1, 0.1];
alpha = 0.001;

% 应该注意，超过二维的样本及其输出结果是画不出来的。
% mX的第一列是x下标0，令其等于1，为了形式统一。要是为了简单，去掉也可以
%   那mX就变成了一维的
% 本例，使用mX的第二列作为x坐标，mY为y坐标绘制图形。
plot(mX(:,2),mY,'o');
hold on;

% 以下的计算过程，在上面的讲解中已经很详细了，来一个万恶的字...
%   略。
error = 1.0;
for i = 1:1000
    i % 为了显示
    mTemp = (mY - mX*mThetas');
    mThetas = mThetas + alpha * mTemp'*mX; 
      
    lasterror = error;
    error = 0.5*mTemp'*mTemp
    
    if(abs(error-lasterror) < 0.1)
        break;
    end
end

mNewY = mX*mThetas';
plot(mX(:,2), mNewY,'r');


end

 

 

# Python例程（3.5）

需要numpy库的支持（free and easy to install）

需要matplotlib库的支持（free and easy to install）

from numpy import *
import matplotlib.pyplot as plt 

def LMS_GD() :
    # 准备样本
    mX = mat([[1,1], [1,2], [1,3], [1,4], [1,5], [1,6], [1,7], [1,8], [1,9]])
    mY = mat([1.1, 1.5, 2.1, 2.9, 3.5, 4.4, 5.1, 6.7, 8.3])
    mY = mY.T # 转置
    mThetas = mat([0.1, 0.1])
    alpha = 0.001 # 太大可能造成不收敛，太小速度太慢

    # 显示
    mlx = mX[0:,1] # 取第二列（序号0初始）
    lx = mlx.tolist();
    ly = mY.tolist();
    plt.plot(lx, ly, 'ro');
    # plt.show()
    
    # 迭代
    error = 1.0
    for i in range(1000) :
        print('run %d times: error = %d' % (i, error))
        
        mTemp = (mY - mX*mThetas.T)
        mThetas = mThetas + alpha * mTemp.T * mX

        lasterror = error;
        error = 0.5*mTemp.T * mTemp

        if abs(error-lasterror) < 0.1 :
            break;


    # 显示
    mNewY = mX*mThetas.T
    ly = mNewY.tolist()
    plt.plot(lx, ly,)
    plt.show()

    return True

 

Bingo!

以上。