遍历
计算机科学中的树
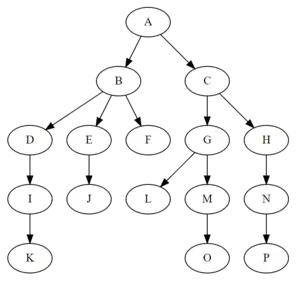
在计算机科学中,树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)
为什么需要树?
因为它结合了另外两种数据结构的优点: 一种是有序数组,另一种是链表。在树中查找数据项的速度和在有序数组中查找一样快, 并且插入数据项和删除数据项的速度也和链表一样。
在有序数组中插入数据项太慢
假设数组中的所有数据项都有序的排列—这就是有序数组,用二分查找法可以在有序数组中快速地查找特定的值。
二分查找法的过程是先査看数组的正中间的数据项,如果那个数据项值比要找的大,就缩小査找范围,在数组的后半段中找;如果小, 就在前半段找。反复这个过程,查找数据所需的时间是O(logN)。同时也可以迅速地遍历有序数组, 按顺序访问每个数据项。
然而,想在有序数组中插入一个新数据项,就必须首先査找新数据项插入的位置,然后把所有 比新数据项大的数据项向后移动一位,来给新数据项腾出空间。这样多次的移动很费时,平均来讲 要移动数组中一半的数据项(N/2次移动)。
删除数据项也需要多次的移动,所以也很慢。 显而易见,如果要做很多的插入和删除操作,就不该选用有序数组。
在链表中查找太慢
链表的插入和删除操作都很快。它们只需要改变一些引用的值就行了。这些操作的时间复杂度是0(1)(是大O表示法中最小的时间复杂度)。
但是在链表中查找数据项可不那么容易。查找必须从头开始,依次访问链表中的每一个数据项,把每个数据项的值和要找的数据项做比较,直到找到该数据项为止,平均需要访问N/2个数据项。这个过程很慢,费时O(N)(注意,对排序来说比较快的,对数据结构操作来说是比较慢的。)。
我们可以通过有序的链表来加快查找速度,链表中的数据项是有序的,但这样做是没有用的。即使是有序的链表还是必须从头开始依次访问数据项,因为链表中不能直接访问某个数据项,必须通过数据项间的链式引用才可以。(当然有序链表访问节点还是比无序链表快多了,但查找任意的数据项时它也无能为力了。)
术语
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 树的度:一棵树中,最大的节点度称为树的度;
- 叶节点或终端节点:度为零的节点;
- 非终端节点或分支节点:度不为零的节点;
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的种类
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
- 有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
- 二叉树:每个节点最多含有两个子树的树称为二叉树;
- 完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树;
- 满二叉树:所有叶节点都在最底层的完全二叉树;
- 平衡二叉树(AVL树):当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
- 排序二叉树(二叉查找树(英语:Binary Search Tree)):也称二叉搜索树、有序二叉树;
- 霍夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树;
- B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多于两个子树。
树的抽象(ADT)
树作为一种抽象的数据类型,至少要支持以下的基本方法
| 方法名 | 描述 |
| getElement() | 返回存放于当前节点处的对象 |
| setElement(e) | 将对象 e 存入当前节点,并返回其中此前所存的内容 |
| getParent() | 返回当前节点的父节点 |
| getFirstChild() | 返回当前节点的长子 |
| getNextSibling() | 返回当前节点的最大弟弟 |
树的实现
使用数组实现
树可以使用数组实现,节点在数组中的位置对应于它在树中的位置。下标为0的节点是根,下标为1的节点是根的左子节点,依次类推,按从左到右的顺序存储树的每一层。
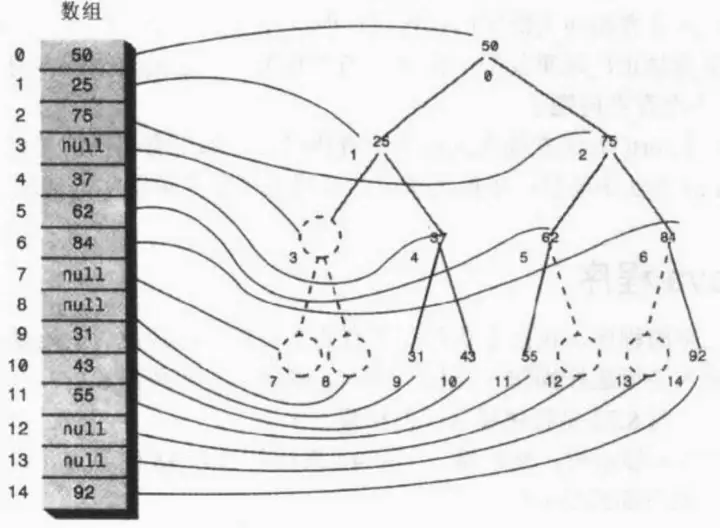
树中的每个位置,无论是否存在节点,都对应数组中的一个位置。把节点插入树的一个位置, 意味着要在数组的相应位置插入一个数据项。树中没有节点的位置在数组中的对应位置用0或null来表示。
基于这种思想,找节点的子节点和父节点可以利用简单的算术计算它们在数组中的索引值。设节点索引值为 indexindex ,则节点的左子节点是: 2×index+12\times index +1 ,它的右子节点是 2×index+22\times index+2 ,它的父节点是 (index−1)÷2\left( index -1 \right)\div 2
大多数情况下用数组表示树不是很有效率。不满的节点和删除掉的节点在数组中留下了洞,浪费存储空间。更坏的是,删除节点时需要移动子树的话,子树中的每个节点都要移到数组中新的位置去,这在比较大的树中是很费时的。
不过,如果不允许删除操作,数组表示可能会很有用。
使用链表实现
/**
* @author keji
* @version : Tree.java, v 0.1 2019-07-18 9:46 keji Exp $$
*/
public interface Tree {
/**
* 返回当前节点中存放的对象
*
* @return Object
*/
Object getElem();
/**
* 将对象obj存入当前节点,并返回此前的内容
*
* @return Object
*/
Object setElem(Object obj);
/**
* 返回当前节点的父节点
*
* @return TreeLinkedList
*/
TreeLinkedList getParent();
/**
* 返回当前节点的长子
*
* @return TreeLinkedList
*/
TreeLinkedList getFirstChild();
/**
* 返回当前节点的最大弟弟
*
* @return TreeLinkedList
*/
TreeLinkedList getNextSibling();
/**
* 返回当前节点后代元素的数目,即以当前节点为根的子树的规模
*
* @return int
*/
int getSize();
/**
* 返回当前节点的高度
*
* @return int
*/
int getHeight();
/**
* 返回当前节点的深度
*
* @return int
*/
int getDepth();
}对应实现
/**
* @author keji
* @version : TreeLinkedList.java, v 0.1 2019-07-18 9:46 keji Exp $$
*/
public class TreeLinkedList implements Tree {
/**
* 树根节点
*/
private Object element;
/**
* 父节点、长子及最大的弟弟
*/
private TreeLinkedList parent, firstChild, nextSibling;
/**
* (单节点树)构造方法
*/
public TreeLinkedList() {
this(null, null, null, null);
}
/**
* 构造方法
*
* @param object 树根节点
* @param parent 父节点
* @param firstChild 长子
* @param nextSibling 最大的弟弟
*/
public TreeLinkedList(Object object, TreeLinkedList parent, TreeLinkedList firstChild, TreeLinkedList nextSibling) {
this.element = object;
this.parent = parent;
this.firstChild = firstChild;
this.nextSibling = nextSibling;
}
@Override
public Object getElem() {
return element;
}
@Override
public Object setElem(Object obj) {
Object bak = element;
element = obj;
return bak;
}
@Override
public TreeLinkedList getParent() {
return parent;
}
@Override
public TreeLinkedList getFirstChild() {
return firstChild;
}
@Override
public TreeLinkedList getNextSibling() {
return nextSibling;
}
@Override
public int getSize() {
//当前节点也是自己的后代
int size = 1;
//从长子开始
TreeLinkedList subtree = firstChild;
//依次
while (null != subtree) {
//累加
size += subtree.getSize();
//所有孩子的后代数目
subtree = subtree.getNextSibling();
}
//得到当前节点的后代总数
return size;
}
@Override
public int getHeight() {
int height = -1;
//从长子开始
TreeLinkedList subtree = firstChild;
while (null != subtree) {
//在所有孩子中取最大高度
height = Math.max(height, subtree.getHeight());
subtree = subtree.getNextSibling();
}
//即可得到当前节点的高度
return height + 1;
}
@Override
public int getDepth() {
int depth = 0;
//从父亲开始
TreeLinkedList p = parent;
while (null != p) {
depth++;
//访问各个真祖先
p = p.getParent();
}
//真祖先的数目,即为当前节点的深度
return depth;
}
}树的遍历
所谓树的遍历(Traversal),就是按照某种次序访问树中的节点,且每个节点恰好访问一次。
也就是说,按照被访问的次序,可以得到由树中所有节点排成的一个序列。
前序遍历
对任一(子)树的前序遍历,将首先访问其根节点,然后再递归地对其下的各棵子树进行前序遍历。对于同一根节点下的各棵子树,遍历的次序通常是任意的;但若换成有序树,则可以按照兄弟间相应的次序对它们实施遍历。由前序遍历生成的节点序列,称作前序遍历序列。
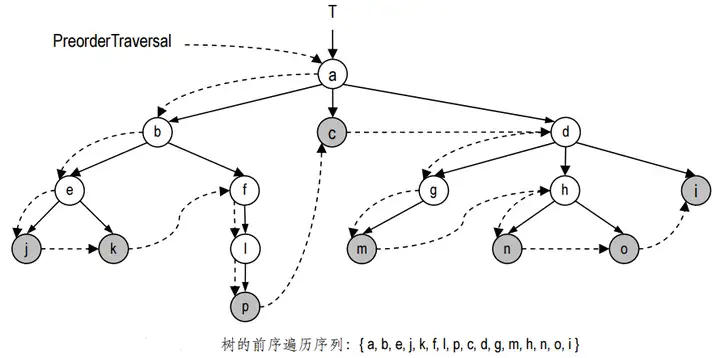
后续遍历
对称地,对任一(子)树的后序遍历将首先递归地对根节点下的各棵子树进行后序遍历,最后才访问根节点。由后序遍历生成的节点序列,称作后序遍历序列。
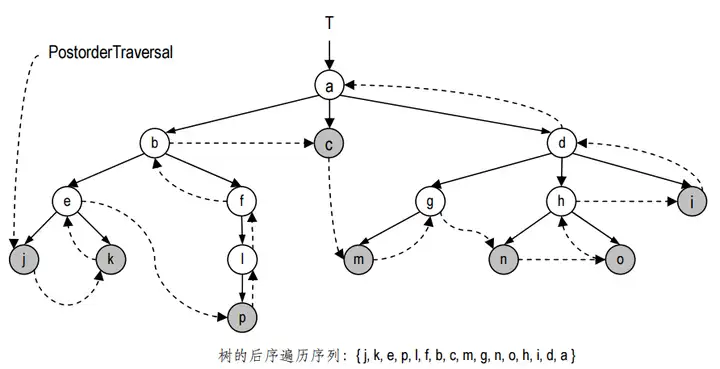
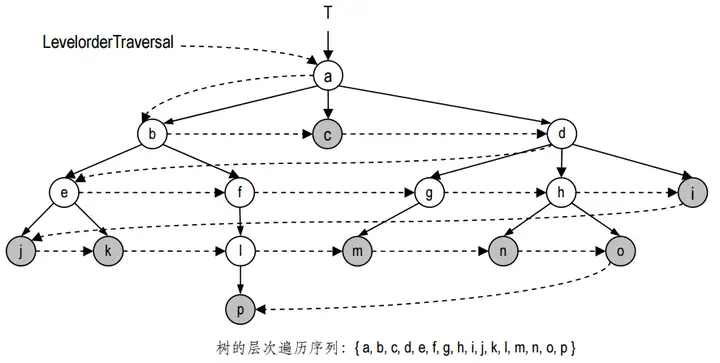
层次遍历
除了上述两种最常见的遍历算法,还有其它一些遍历算法,层次遍历(Traversal by level )算法就是其中的一种。在这种遍历中,各节点被访问的次序取决于它们各自的深度,其策略可以总结为“深度小的节点优先访问”。
对于同一深度的节点,访问的次序可以是随机的,通常取决于它们的存储次序,即首先访问由firstChild指定的长子,然后根据nextSibling确定后续节点的次序。当然,若是有序树,则同深度节点的访问次序将与有序树确定的次序一致。
下一篇



