初等数论学习笔记 III：数论函数与筛法
1. 数论函数
本篇笔记所有内容均与数论函数相关。因此充分了解各种数论函数的名称，定义，符号和性质是必要的。
1.1 相关定义
- 数论函数：定义域为正整数的函数称为 数论函数。因其在所有正整数处均有定义，故可视作数列。OI 中常见的数论函数的陪域（即可能的取值范围）为整数。
- 加性函数：若对于任意 \(a, b\in \mathbb{N}_+\) 且 \(a\perp b\) 均有 \(f(ab) = f(a) + f(b)\)，则称 \(f\) 为 加性函数。注意区分代数中的加性函数。
- 积性函数：若对于任意 \(a, b\in \mathbb{N}_+\) 且 \(a\perp b\) 均有 \(f(ab) = f(a)f(b)\)，则称 \(f\) 为 积性函数。易知 \(f(1) = 1\) 是必要条件。
- 完全积性函数：若对于任意 \(a, b\in \mathbb{N}_{+}\) 均有 \(f(ab) = f(a)f(b)\)，则称 \(f\) 为 完全积性函数。完全积性函数一定是积性函数。
- 数论函数的 加法：对于数论函数 \(f, g\)，\(f + g\) 表示 \(f\) 和 \(g\) 对应位置相加，即 \((f + g)(x) = f(x) + g(x)\)。
- 数论函数的 数乘：对于数 \(c\) 和数论函数 \(f\)，\(c\cdot f\) 表示 \(f\) 的各个位置乘 \(c\)，即 \((c\cdot f)(x) = c \cdot f(x)\)。一般简记作 \(cf\)。
- 数论函数的 点乘：对于数论函数 \(f, g\)，\(f \cdot g\) 表示 \(f\) 和 \(g\) 对应位置相乘，即 \((f \cdot g)(x) = f(x)g(x)\)。为与狄利克雷卷积符号 \(*\) 作区分，点乘符号通常不省略。
1.2 常见数论函数
设 \(n\) 的唯一分解为 \(\prod\limits_{i = 1} ^ m p_i ^ {c_i}\)，以下是一些常见数论函数：
- 单位函数：\(\epsilon(n) = [n = 1]\)。当 \(n = 1\) 时取值为 \(1\)，否则取值为 \(0\)。它是完全积性函数。
- 常数函数：\(1(n) = 1\)。它是完全积性函数。
- 恒等函数：\(\mathrm{id}_k(n) = n ^ k\)。\(\mathrm{id}_1(n)\) 记作 \(\mathrm {id}(n)\)。它是完全积性函数。
- 除数函数：\(\sigma_k(n) = \sum\limits_{d\mid n}d ^ k\)。\(\sigma_0(n)\) 表示 \(n\) 的约数个数，记作 \(\tau(n)\) 或 \(d(n)\)。\(\sigma_1(n)\) 表示 \(n\) 的约数和，记作 \(\sigma(n)\)。\(\sigma_k(n)\) 有计算式 \(\begin{cases} \prod\limits_{i = 1} ^ m (c_i + 1) & k = 0 \\ \sum\limits_{i = 1} ^ m \frac{p_i ^ {(c_i + 1)k} - 1}{p_i - 1} & k > 0\end{cases}\)：根据乘法分配律，\(n\) 的所有约数的 \(k\) 次方之和可写作 \(\prod\limits_{i = 1} ^ m\sum\limits_{j = 0} ^ {c_i} p_i ^ {jk}\)，等比数列求和后即得。
- 欧拉函数：\(\varphi(n) = \sum\limits_{i = 1} ^ n[i\perp n]\)，表示 \(n\) 以内与 \(n\) 互质的数的个数。关于欧拉函数的性质，详见笔记 I.
- 本质不同质因子个数函数：\(\omega(n) = \sum\limits_{p \in \mathbb{P}} [p\mid n]\)，表示 \(n\) 的本质不同质因子个数。
- 莫比乌斯函数：\(\mu(n) = \begin{cases} 1 & n = 1 \\ 0 & \exists d > 1, d ^ 2\mid n \\ (-1) ^ {\omega(n)} & \mathrm{otherwise} \end{cases}\)。
以上所有函数除 \(\omega\) 是加性函数以外，其余均为积性函数。根据计算式及积性函数的定义易证。
2. 素数筛法
素数筛法是数论体系中最基本的知识点，几乎所有数论题目都需要筛出 \(1\sim n\) 的所有素数。
2.1 埃氏筛素数
埃氏筛用所有已经筛出的素数的倍数标记合数：从 \(2\) 到 \(n\) 枚举所有数 \(i\)，若 \(i\) 未被标记，则 \(i\) 是质数，将 \(i\) 除 \(i\) 以外的倍数标记为合数。
for(int i = 2; i < N; i++)
if(!vis[i]) {
pr[++cnt] = i;
for(int j = 2 * i; j < N; j += i) vis[j] = 1;
}
常数优化：根据合数 \(i\) 的最小质因子 \(\leq \sqrt i\)，可以从 \(i ^ 2\) 开始标记。
for(int i = 2; i < N; i++)
if(!vis[i]) {
pr[++cnt] = i;
if(1ll * i * i < N) // 防止 i * i 溢出导致 RE
for(int j = i * i; j < N; j += i) vis[j] = 1;
}
埃氏筛的精髓在于其复杂度证明：不超过 \(n\) 的质数的倒数之和为 \(\mathcal{O}(\ln \ln n)\) 级别。
这说明埃氏筛的复杂度为 \(\mathcal{O}(n\ln \ln n)\)。
证明来自戴江齐学长：
因为每个数只会被其素因子筛到，所以 \(\sum\limits_{p\in \mathbb{P}, p\leq n} \dfrac 1 p = \sum\limits_{i = 1} ^ n \omega(i)\)。
根据 \(d(i)\) 的计算式，\(\sum\limits_{i = 1} ^ n 2 ^ {\omega(i)} \leq \sum\limits_{i = 1} ^ n d(i) = \mathcal{O}(n\ln n)\)。
根据 \(2 ^ x\) 的凸性和琴生不等式得 \(\sum\limits_{i = 1} ^ n 2 ^ {\omega(i)} \geq n 2 ^ {\frac{\sum_{i = 1} ^ n \omega(i)} n}\)，所以 \(2 ^ {\frac{\sum_{i = 1} ^ n \omega(i)} n} \leq \mathcal{O}(\ln n)\)。
两边同时取对数，\(\dfrac {\sum_{i = 1} ^ n \omega(i)} n \leq \mathcal{O}(\ln \ln n)\)，因此 \(\sum\limits_{i = 1} ^ n \omega(i)\leq \mathcal{O}(n\ln\ln n)\)。证毕。
2.2 线性筛素数
线性筛也称欧拉筛，它和埃氏筛的思想类似。
埃氏筛的优秀之处在于仅用质数的倍数筛去合数，但合数会被多个质因子筛到。让每个合数仅被筛一次就能做到线性。
考虑用每个合数的 最小质因子 筛去它：从 \(2\) 到 \(n\) 枚举所有数 \(i\)。对于每个 \(i\)，令其最小质因子为 \(p\)，则对于不大于 \(p\) 的质数 \(q\)，\(iq\) 的最小质因子为 \(q\)。将所有 \(iq\) 标记为合数，则每个合数 \(c\) 仅在 \(i = \dfrac c m\) 时以 \(im\) 的形式删去，其中 \(m\) 是 \(c\) 的最小质因子。
综上，有如下步骤：
- 从小到大遍历当前筛出的所有素数 \(pr_j\)，将 \(i\times pr_j\) 标记为合数。
- 若 \(pr_j\mid i\)，退出循环。因为 \(pr_j\mid i\times pr_k(k > j)\)，所以 \(i\times pr_k\) 的最小质因子为 \(pr_j\) 不是 \(pr_k\)，再筛就重复了。
时间复杂度线性。模板题 P3383 代码如下：
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1e8 + 5;
bool vis[N];
int n, q, pr[N / 16], cnt;
int main() {
cin >> n;
for(int i = 2; i <= n; i++) {
if(!vis[i]) pr[++cnt] = i;
for(int j = 1; j <= cnt && i * pr[j] <= n; j++) {
vis[i * pr[j]] = 1;
if(i % pr[j] == 0) break;
}
}
cin >> q;
while(q--) {
int x;
scanf("%d", &x);
printf("%d\n", pr[x]);
}
return 0;
}
2.3 线性筛积性函数
线性筛提供了在线性时间内筛出具有特殊性质的积性函数在 \(1\sim n\) 处所有取值的基本框架。
只要积性函数 \(f\) 可在 \(\mathcal{O}(1)\) 时间内计算任意质数幂处的取值 \(f(p ^ k)\)，就适用线性筛。
- 注意，这只是 \(f\) 可线性筛的 充分但不必要 条件。存在更弱的条件使得 \(f\) 可线性筛但并不常见，如 \(\mathcal{O}(k)\) 计算 \(f(p ^ k)\)，这将在第三章介绍。
根据积性函数的性质，只要预先求出 \(low_i\) 表示 \(i\) 的最小质因子 \(p\) 的最高次幂 \(p ^ {v_p(i)}\)，对于 \(i\neq p ^ k\)，即可使用 \(f(low_i)f\left(\dfrac i {low_i}\right)\) 计算 \(f(i)\)。关于符号 \(v_p(n)\) 详见笔记 I 基本定义与记号。
for(int i = 2; i < N; i++) {
if(!vis[i]) pr[++pcnt] = i, f[i] = ..., low[i] = i; // 单独算 f(p)
for(int j = 1; j <= pcnt && i * pr[j] < N; j++) {
vis[i * pr[j]] = 1;
if(i % pr[j] == 0) { // i 与 p 不互质
low[i * pr[j]] = low[i] * pr[j];
if(i == low[i]) f[i * pr[j]] = ...; // i = p ^ k，单独算 f(p ^ {k + 1})
else f[i * pr[j]] = f[i / low[i]] * f[low[i * pr[j]]];
break;
}
low[i * pr[j]] = pr[j];
f[i * pr[j]] = f[i] * f[pr[j]]; // i 与 p 互质，f(ip) = f(i)f(p)
}
}
3. 狄利克雷卷积
狄利克雷（Dirichlet）卷积是数论函数的基本运算，其重要程度相当于代数中的四则运算。
3.1 定义与性质
为数列定义卷积，自然想到加法卷积 \(c_k = \sum\limits_{i + j = k} a_ib_j\)，但加法卷积不能保留积性。让我们发散想象力，如果将加法换成乘法，结果如何？这引出了 狄利克雷卷积：
上式简记为 \(h = f * g\)。按照定义式计算狄利克雷卷积，复杂度为调和级数的 \(\mathcal{O}(n\ln n)\)。
接下来证明一些狄利克雷卷积的性质。
性质 1：狄利克雷卷积具有 交换律，结合律，分配律。
交换律：
其中 \(d' = \dfrac n d\)。因此 \(f * g = g * f\)。
结合律：
其中 \(k = \dfrac d i\)。因此 \((f * g) * h = f * (g * h)\)。
分配律：
因此 \((f + g) * h = f * h + g * h\)。证毕。
性质 2：\(\epsilon * f = f\)。
证明：\((\epsilon * f)(n) = \sum\limits_{d \mid n}[d = 1]f\left(\dfrac n d\right) = f(n)\)。证毕。
因此单位函数 \(\epsilon\) 为狄利克雷卷积的 单位元。
既然存在单位元，就可以据此定义数论函数 \(f\) 的逆元 \(f ^ {-1}\)，满足 \(f * f ^ {-1} = \epsilon\)。
性质 3：\(f\) 可逆当且仅当 \(f(1)\neq 0\)。
证明：设 \(g = f ^ {-1}\)。当 \(f(1) = 0\) 时，\(f(1)g(1) = 0\) 且 \(f(1) g(1) = \epsilon(1) = 1\)，矛盾。当 \(f(1) \neq 0\) 时，\(g(1) = \dfrac 1 {f(1)}\)，对 \(n > 1\) 的 \(g(x)\) 通
过 \(\sum\limits_{d\mid x} g(d)f\left(\dfrac n d\right) = 0\) 得到递推式 \(g(n) = -\dfrac{\sum\limits_{d \mid n, d \neq n} g(d)f\left(\dfrac n d\right)} {f(1)}\)。这同时说明 逆元唯一。证毕。
性质 4：\(f = g\) 的充要条件是 \(f * h = g * h\)，其中 \(h(1) \neq 0\)。
证明：\(f * h = g * h\Rightarrow f * h * h ^ {-1} = g * h * h ^ {-1} \Rightarrow f = g\)，充分性得证。必要性显然。证毕。
性质 5：积性函数的狄利克雷卷积是积性函数。
证明：考虑积性函数 \(f\) 和 \(g\) 的狄利克雷卷积 \(h\)。若 \(a\perp b\)，则
其中 \(d = d_1d_2\)。第二步依赖于 \(f\) 和 \(g\) 的积性：\(f(d_1) f(d_2) = f(d_1d_2) = f(d)\)。证毕。
性质 6：积性函数的逆元是积性函数。
证明：设 \(g = f ^ {-1}\)。根据 \(f\) 的积性可知 \(g(1) = \dfrac 1 {f(1)} = 1\)，所以 \(g(n) = g(1) g(n)\)。
考虑归纳法。对于 \(n, m > 1\) 且 \(n\perp m\)，假设对于任意 \(xy < nm\) 且 \(x\perp y\) 均有 \(g(xy) = g(x)g(y)\)。因 \(n = 1\) 或 \(m = 1\) 时命题成立，只需证明 \(g(nm) = g(n)g(m)\)。
因为 \(n, m > 1\)，所以 \(\epsilon(n) = \epsilon(m) = 0\)，所以 \(g(nm) = g(n)g(m)\)。证毕。
综合性质 5 和性质 6，两个积性函数的积与商都是积性函数。注意，积性函数的和与差不是积性函数。
3.2 线性筛 Dirichlet 卷积
根据积性函数的狄利克雷卷积是积性函数这一结论，我们尝试在线性时间内筛出 \(h = f * g\)。
写出 \(h\) 的表达式，有
对于第一和第三种情况，线性筛时可以总代价 \(\mathcal{O}(n)\) 求出。关键在于 Case 2，若 \(f\) 和 \(g\) 在质数幂处的取值已经求出，则需要 \(\mathcal{O}(k)\) 的时间计算。
- 特别的，当 \(f\) 为完全积性函数时，\(h(p ^ k)\) 可以写作 \(f(p)h(p ^ {k - 1}) + g(p ^ k)\)，可以 \(\mathcal{O}(1)\) 方便地计算。对于 \(g\) 同理。
尝试估计第二部分的复杂度。考虑到所有小于 \(\leq \sqrt[k]n\) 的质数会对复杂度产生 \(\mathcal{O}(k)\) 的贡献，因此
感性理解，\(x ^ 2 \sqrt[x]{n}\) 随着 \(n\) 增大，\(x\) 增大时 \(x ^ 2\) 一项增大的速度远小于 \(\sqrt[x]{n}\) 衰减的速度。从这一点入手，考虑证明 \(x ^ 2 \sqrt[x] n \leq \mathcal{O}(n)\)。
当 \(x = 1\) 时显然成立，否则考虑 \(x\in [2, \log_2 n]\) 时 \(x ^ 2\) 的最大值 \(\log_2 ^ 2 n\) 与 \(\sqrt[x] n\) 的最大值 \(\sqrt n\) 之积，因为当 \(x\to +\infty\) 时 \(\log_2 x\) 是 \(\sqrt x\) 的高阶无穷小，所以 \(\mathcal{O}(\sqrt n\log ^ 2 n) \leq \mathcal{O}(n)\)。
因此，\(T(n) \leq \dfrac 1 {\ln n} \sum\limits_{i = 1} ^ {\log_2 n} \mathcal{O}(n) = \mathcal{O}(n)\)。
综上，使用线性筛求出两个在质数幂处取值已知的积性函数的狄利克雷卷积在 \(1\sim n\) 处的取值的时间复杂度为 \(\mathcal{O}(n)\)。
我们得到了积性函数可线性筛的更弱的条件：可以 \(\mathcal{O}(k)\) 时间计算质数幂处的取值。
3.3 狄利克雷前缀和
前置知识：高维前缀和。
任意数论函数 \(f\) 卷常数函数 \(1\) 等价于对 \(f\) 做 狄利克雷前缀和：令 \(g = f * 1\)，则 \(g(n) = \sum\limits_{d\mid n} f(d)\)。
对每个 \(n\) 计算给定数论函数在其所有因数处的取值之和有很好的实际含义，因此狄利克雷前缀和是比较重要的算法。
将每个数 \(n\) 写成无穷序列 \(a_n = \{c_1, c_2, \cdots, c_i, \cdots\}\) 表示 \(n = \prod p_i ^ {c_i}\)，其中 \(p_i\) 表示第 \(i\) 个质数。因为 \(x\mid y\) 的充要条件为 \(a_x(c_i) \leq a_y(c_i)\)，所以 \(f * 1\) 可以看成对下标做关于其无穷序列的高维前缀和，即 \(g(n) = \sum\limits_{\forall i, a_d(c_i) \leq a_n(c_i)} f(d)\)。
根据高维前缀和的求法，枚举每一维并将所有下标关于该维做前缀和，可得狄利克雷前缀和的实现方法：初始令 \(x_i = f(i)\)。从小到大枚举每个质数 \(p_i\)，枚举 \(k\)，将 \(x_{p_ik}\) 加上 \(x_k\)，相当于 \(k\) 贡献到给 \(a_k(i)\) 加上 \(1\) 之后的下标。最终得到的 \(x\) 即为 \(g\)。
根据小于 \(n\) 的素数倒数之和为 \(\ln\ln n\) 这一结论，狄利克雷前缀和的时间复杂度为 \(\mathcal{O}(n\ln\ln n)\)。
模板题 P5495 代码。
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e7 + 5;
int n;
unsigned ans, a[N], seed;
inline unsigned rd() {
seed ^= seed << 13, seed ^= seed >> 17, seed ^= seed << 5;
return seed;
}
bool vis[N];
int cnt, pr[N >> 3];
void sieve() {
for(int i = 2; i <= n; i++) {
if(!vis[i]) pr[++cnt] = i;
for(int j = 1; j <= cnt && i * pr[j] <= n; j++) {
vis[i * pr[j]] = 1;
if(i % pr[j] == 0) break;
}
}
}
int main() {
cin >> n >> seed, sieve();
for(int i = 1; i <= n; i++) a[i] = rd();
for(int i = 1; i <= cnt; i++)
for(int j = 1; j * pr[i] <= n; j++)
a[j * pr[i]] += a[j];
for(int i = 1; i <= n; i++) ans ^= a[i];
cout << ans << endl;
return 0;
}
4. 数论分块
数论分块又称整除分块，因其解决的问题与整除密切相关而得名。数论分块用于求解形如
的和式。前提为 \(f\) 的前缀和可快速计算。
感性认知：使得 \(\left\lfloor\dfrac n x\right\rfloor = k\) 的正整数 \(x\) 的范围为 \(\left(\left\lfloor \dfrac n {k + 1}\right\rfloor, \left\lfloor \dfrac n k\right\rfloor \right]\)。
4.1 算法介绍
如果 \(\left\lfloor\dfrac n i\right\rfloor\) 的数量不多，可以考虑转换贡献形式，将原式写成若干 \(g\left(\left\lfloor\dfrac n i\right\rfloor\right)\) 乘以一段 \(f\) 的和。接下来分析不同 \(\left\lfloor\dfrac n i\right\rfloor\) 的数量的上界。
当 \(i\) 较大时，\(\left\lfloor \dfrac {n} {i} \right\rfloor\) 被限制在较小范围内，很多 \(\left\lfloor \dfrac {n} {i}\right\rfloor\) 均相同。结合 \(\min\left(i, \dfrac n i\right) \le \sqrt n\)，可以想到根号分治。
结论 1：对于任意 \(i\in [1, n], n\in \mathbb N_+\)，不同的 \(\left\lfloor \dfrac {n} {i}\right\rfloor\) 至多 \(2\sqrt n\) 个。
证明：\(i \leq \sqrt n\) 时，\(\left\lfloor \dfrac {n} {i}\right\rfloor\) 只有 \(\sqrt n\) 个；\(i > \sqrt n\) 时，\(\left\lfloor \dfrac {n} {i}\right\rfloor \leq \sqrt n\)，只有 \(\sqrt n\) 个。证毕。
根据结论 1，枚举 \(\mathcal{O}(\sqrt n)\) 种整除值 \(d\)，求出最小和最大的 \(i\) 使得 \(\left\lfloor\dfrac n i\right\rfloor = d\)，分别记作 \(l, r\)，则原式可写为 \(\sum\limits_{d} g(d)\sum\limits_{i = l} ^ r f(i)\)。因此，只要 \(f\) 的前缀和可以快速计算，\(g\) 在某处的取值可以快速得到，即可在 \(\mathcal{O}(\sqrt n)\) 的时间内解决原问题。
这样，问题转化为求使得 \(\left\lfloor\dfrac n i\right\rfloor = d\) 的最小和最大的 \(i\)。
\(\left\lfloor\dfrac n i\right\rfloor = d\) 对 \(i\) 有两条限制，分别为 \(i(d + 1) > n\) 和 \(id \leq n\)。因为使得 \(id\leq n\) 的最大的 \(i\) 就是 \(\left\lfloor\dfrac n d\right\rfloor\)，同理使得 \(i(d + 1) \leq n\) 的最大的 \(i\) 为 \(\left\lfloor\dfrac n {d + 1}\right\rfloor\)，所以 \(l = \left\lfloor\dfrac n {d + 1}\right\rfloor + 1\)，\(r = \left\lfloor\dfrac n d\right\rfloor\)。
如何不重不漏地枚举所有整除值？没有必要。我们只需依次枚举每个 \(i\)，并借助上述工具跳过 \(\left\lfloor\dfrac n i\right\rfloor\) 相同的极长连续段即可。
具体地，令当前枚举到的 \(i\) 为 \(l\)，此时整除值为 \(d = \left\lfloor\dfrac n i\right\rfloor\)。因为使得 \(\left\lfloor\dfrac n i\right\rfloor = d\) 的最大的 \(i\) 等于 \(\left\lfloor\dfrac n d\right\rfloor\)，所以令 \(r = \left\lfloor\dfrac n {\left\lfloor\frac n l\right\rfloor}\right\rfloor\)，将 \(g(d)(s(r) - s(l - 1))\) 累和入答案，并令 \(l \gets r + 1\) 表示跳过 \(l + 1\sim r\) 这一段 \(i\)，若 \(l > n\) 则退出。其中 \(s\) 是 \(f\) 的前缀和。
每个整除值仅会被遍历一次，时间复杂度 \(\mathcal{O}(\sqrt n)\)。
- 注意，当 \(i\) 的上界不等于 \(n\) 时，设其为 \(m\)，则 \(r\) 应与 \(m\) 取较小值（处理 \(n > m\) 的情况），且当 \(\left\lfloor\dfrac n i\right\rfloor = 0\) 时需要特判，直接令 \(r\) 等于 \(m\)（处理 \(n < m\) 的情况）。
4.2 扩展
4.2.1 向上取整
尝试将向下取整变为向上取整。
对于左边界 \(l\)，求出使得 \(\left\lceil\dfrac n l \right\rceil = \left\lceil\dfrac n r \right\rceil\) 的最大的 \(r\)。不妨设 \(k = \left\lceil\dfrac n l\right\rceil\)，则
第三步转换是因为 \(n, k\) 均为正整数。因此，只需令 \(r\gets \left\lfloor\dfrac{n - 1}{\left\lceil\frac n l\right\rceil - 1}\right\rfloor\) 即可。
注意特判 \(\left\lceil\dfrac n l\right\rceil=1\)，此时 \(r\) 的上界为无穷大，需要取实际上界。
4.2.2 高维数论分块
当和式中出现若干下取整，形如
时，只需稍作修改，令 \(r = \min\limits_{j = 1} ^ c\left(\left\lfloor \dfrac {n_j} {\left\lfloor \frac {n_j} l\right\rfloor}\right\rfloor\right)\) 即可。不要忘记对 \(n\) 取 \(\min\)。
时间复杂度为 \(\sum \sqrt {n_j}\)。将使得存在 \(n_j\) 满足 \(\left\lfloor \dfrac {n_j} {i}\right\rfloor \neq \left\lfloor \dfrac {n_j} {i + 1}\right\rfloor\) 的位置 \(i\) 视作断点，则总断点数量为每个下取整式的端点数量相加而非相乘。我们只会在每相邻两个断点形成的区间处遍历一次，故有该时间复杂度。
4.3 例题
I. [模拟赛] 你还没有卸载吗
给定 \(A_1, B_1, A_2, B_2, N\)，求有多少 \(x\in [1, N]\) 使得 \(B_1 + \left\lfloor\dfrac{A_1}{x}\right\rfloor = B_2 + \left\lfloor\dfrac{A_2}{x}\right\rfloor\)。\(T\leq 2\times 10 ^ 3\)，其他所有数 \(\in [1, 10 ^ 8]\)。时限 1s。
考虑数论分块 \([l, r]\) 固定 \(\dfrac{A_1} x\)，解出 \(d = \dfrac{A_2}{x}\)，反推出合法的 \(x\) 的范围：\([l, r] \cap \left[\dfrac{A_2}{d + 1} + 1, \dfrac{A_2}{d}\right]\)。时间复杂度 \(\mathcal{O}(T\sqrt V)\)。
另一种方法是直接二维数论分块。细节更少，且时间复杂度相同。
#include <bits/stdc++.h>
using namespace std;
int T, a1, b1, a2, b2, n;
int main() {
cin >> T;
while(T--) {
int ans = 0;
cin >> a1 >> b1 >> a2 >> b2 >> n;
for(int l = 1, r = 1; l <= n; l = r + 1) {
r = min(n, min(a1 / l ? a1 / (a1 / l) : n, a2 / l ? a2 / (a2 / l) : n));
if(b1 + a1 / l == b2 + a2 / l) ans += r - l + 1;
}
cout << ans << endl;
}
return 0;
}
*II. CF1603C Extreme Extension
数论分块优化 DP。
一个数如何分裂由后面分裂出来的数的最小值决定，显然贪心使分出来的数尽量均匀，例如若 \(9\) 要裂成若干个比 \(4\) 小的数，那么 \(3, 3, 3\) 比 \(2, 3, 4\) 更优。
从后往前考虑，对于每个数 \(a_i\) 和值 \(j\in [1, a_i]\)，求出有多少以 \(a_i\) 开头的子串根据上述贪心策略分裂出的最小值为 \(j\)，\(j\) 由 \(a_i\) 分裂零次或若干次得到，记为 \(f_{i, j}\)。
首先明确两点：
- \(a_i\) 分裂成若干 \(\leq v\) 的数，最少分裂次数为 \(\left\lceil \dfrac {a_i} v \right\rceil - 1\)，分裂成 \(\left\lceil \dfrac {a_i} v \right\rceil\) 个数。
- \(a_i\) 分裂成 \(v\) 个数，这些数最小值的最大值为 \(\left\lfloor \dfrac {a_i} v \right\rfloor\)。
考虑转移。
注意到对于固定的分裂次数，分裂出的值也是确定的。考虑枚举使得分裂次数相同的区间 \([l, r]\)，即 \(a_i\) 整除 \([l, r]\) 内所有数向上取整的结果相同，可以通过向上取整的数论分块实现。
令 \(c = \left\lceil \dfrac {a_i} l \right\rceil\) 表示分裂出的数的个数，则分裂出的数的最小值为 \(v = \left\lfloor \dfrac {a_i} c \right\rfloor\)。因此，\(\sum\limits_{j = l} ^ r f_{i + 1, j}\) 转移到 \(f_{i, v}\)。
考虑在每个位置处统计该位置在所有子段中总分裂次数之和，则答案加上 \(i\times (c - 1) \times f_{i , v}\)。其含义为，共有 \(f_{i, v}\) 个子段使得 \(a_i\) 要分裂出 \(c\) 个数，即分裂 \(c - 1\) 次。同时，若子段 \([i, k]\) 在 \(i\) 处分裂 \(c - 1\) 次，则对于任意子段 \([x, k]\) 满足 \(1\leq x\leq i\)，\(a_i\) 分裂的次数都是 \(c - 1\)，因为 \(a_i\) 的分裂不受前面的数的影响。
注意，当 \(c = 1\) 时，\(f_{i, v}\) 即 \(f_{i, a_i}\) 需要加上 \(1\)，表示新增以 \(a_i\) 结尾的子段。
用 vector 存储所有 \(f_i\) 并转移，时间复杂度 \(\mathcal{O}(n\sqrt {a_i})\)。滚动数组优化后空间复杂度 \(\mathcal{O}(n)\)。代码。
III. P2260 [清华集训2012] 模积和
求 \(\sum\limits_{i = 1} ^ n n \bmod i\) 是经典问题：拆成 \(\sum\limits_{i = 1} ^ n \left(n - \left\lfloor\dfrac n i\right\rfloor i\right)\) 后数论分块，时间复杂度 \(\mathcal{O}(\sqrt n)\)。
原式可写作
全部使用数论分块解决。可能需要的公式：\(\sum\limits_{i = 1} ^ ni ^ 2 = \dfrac{n(n + 1)(2n + 1)} 6\)。
时间复杂度 \(\mathcal{O}(\sqrt n)\)，代码。
*IV. P3579 [POI2014] PAN-Solar Panels
非常不错的题目。
当 \(\lfloor\frac {a - 1} k\rfloor < \lfloor\frac b k\rfloor\) 且 \(\lfloor\frac{c - 1} k\rfloor < \lfloor\frac d k\rfloor\) 时，\([a, b]\) 和 \([c, d]\) 均含有 \(k\) 的倍数。答案为所有这样的 \(k\) 的最大值。
我们当然可以四维数论分块，但注意到在使得 \(\lfloor\frac b k \rfloor\) 相同且 \(\lfloor \frac d k\rfloor\) 相同的 \(k\) 的区间 \([l, r]\) 当中，选择 \(k = r\) 可以使 \(\lfloor \frac{a - 1} k\rfloor\) 和 \(\lfloor \frac {c - 1} k\rfloor\) 尽可能小，更有机会满足要求。也就是说，若 \(k = r\) 都不满足条件，则 \(l\leq k \leq r\) 均不满足条件。因此二维数论分块即可。
时间复杂度 \(\mathcal{O}(T\sqrt V)\)，代码。
5. 莫比乌斯函数
前置知识：容斥原理。
到达数论最高城，莫比乌斯反演！太好用啦莫反，哎呀这不 GCD 么，还是枚举倍数吧家人们。
5.1 引入
观察 \(\mu(n)\) 的定义式 \(\begin{cases} 1 & n = 1 \\ 0 & \exists d > 1, d ^ 2\mid n \\ (-1) ^ {\omega(n)} & \mathrm{otherwise} \end{cases}\)，读者也许会好奇数学家为什么要定义如此奇怪的函数。这背后必然隐藏着其某种神秘而重要的性质。
\(g(n) = \sum\limits_{d\mid n} f(d)\) 的狄利克雷前缀和形式相当常见，因此根据 \(g\) 求原函数 \(f\) 也很重要。因为 \(g = f * 1\)，所以 \(f = g * 1 ^ {-1}\)。
设 \(h = 1 ^ {-1}\)，根据逆元递推式推导 \(h\) 的一般形式。先将递推式写出，\(h(n) = -\sum\limits_{d\mid n, d\neq n} h(d)\)。
由于积性函数的逆元具有积性，所以 \(h\) 具有积性。只需观察 \(h\) 在质数幂 \(p ^ k\) 处的取值即可得到一般化的结论。
- \(h(p) = -h(1) = -1\)。
- \(h(p ^ 2) = -(h(1) + h(p)) = 0\)。
- \(h(p ^ 3) = -(h(1) + h(p) + h(p ^ 2)) = 0\)。
据此，可归纳证明 \(h(p ^ k)\) 当 \(k = 0\) 时等于 \(1\)，\(k = 1\) 时等于 \(-1\)，\(k \geq 2\) 时等于 \(0\)。
考虑 \(n = \prod\limits_{i = 1} ^ m p_i ^ {c_i}\)。根据 \(h\) 的积性，若存在 \(c_i\geq 2\) 则 \(h(n) = 0\)，否则 \(h(n)\) 等于 \((-1) ^ m\)。容易发现这与莫比乌斯函数的定义式相符。因此 \(1 ^ {-1} = \mu\)，即
验证：令 \(S(n) = \sum\limits_{d\mid n} \mu(d)\)。考虑 \(n\) 的所有质因子 \(p_1 \sim p_m\)。对于任意 \(k\) 个质因子的乘积 \(P\)，它产生 \(\mu(P) = (-1) ^ k\) 的贡献。因此，\(S(n)\) 可写作 \(\sum\limits_{i = 0} ^ m (-1) ^ i\dbinom m i = (1 - 1) ^ m\)。当 \(m = 0\) 时，\(n = 1\)，\(S(n)\) 显然为 \(1\)。否则 \(S(n) = 0 ^ m = 0\)。这从另一个角度说明了 \(\mu * 1 = \epsilon\)。
也可以从容斥系数的角度理解莫比乌斯函数。设 \(g(n) = \sum\limits_{n\mid d} f(d)\)，即 \(g(n)\) 是 \(f\) 在所有 \(n\) 的倍数处的取值和。现在已知 \(g\)，要求 \(f(1)\)。则 \(f(1)\) 等于 \(f\) 在 \(1\) 的倍数处的取值和，减去在质数处的取值和，但是多减去了在两个不同质数乘积处的取值和，因此要加上这些值，但是多加上了在三个不同质数乘积处的取值和，以此类推。因此，若 \(n\) 为 \(k\) 个不同质数的乘积，则 \(f(1)\) 会受到 \(g(n)\) 系数为 \((-1) ^ k\) 的贡献，如下图，图源。
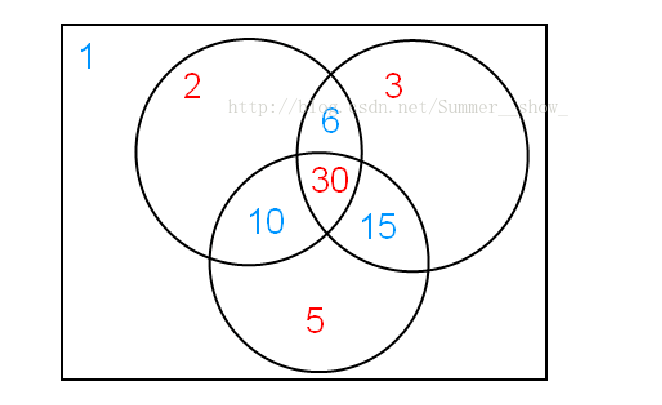
换言之，对 \(\pmb {\mathbb N}\) 做容斥原理，得到贡献系数 \(\boldsymbol \mu\)。
5.2 筛
据定义，线性筛莫比乌斯反演是容易的。
int vis[N], cnt, pr[N], mu[N];
void sieve() {
mu[1] = 1;
for(int i = 2; i < N; i++) {
if(!vis[i]) pr[++cnt] = i, mu[i] = -1;
for(int j = 1; j <= cnt && i * pr[j] < N; j++) {
vis[i * pr[j]] = 1;
if(i % pr[j] == 0) break; // 此时 i * pr[j] 含至少两个 pr[j]，mu = 0
mu[i * pr[j]] = -mu[i]; // mu[i * pr[j]] = mu[i] * mu[pr[j]] = -mu[i]
}
}
}
当时间复杂度可接受时，根据 \(\mu\) 的狄利克雷卷积求逆式 \(\mathcal{O}(n\log n)\) 递推更方便。
int mu[N];
void sieve() {
mu[1] = 1;
for(int i = 1; i < N; i++)
for(int j = i + i; j < N; j += i)
mu[j] -= mu[i];
}
5.3 莫比乌斯反演
\(\mu * 1 = \epsilon\) 引出了 \(\mu\) 的关键性质：\([n = 1] = \epsilon(n) = \sum\limits_{d\mid n} \mu(d)\)。这使得我们可以用 \(\mu\) 的和式代替形如 \([n = 1]\) 的艾佛森括号，体现出其核心 “反演”。
- 用和式代替判断式往往重要但不直观，所以初学者难以理解 OI 常见反演技巧。例如，对于奇质数 \(p\) 有 \(\sum\limits_{x = 1} ^ {p - 1} [x ^ 2 = a] = \left(\dfrac a p\right) + 1 = (a ^ {\frac{p - 1} 2} \bmod p) + 1\)；单位根反演 \([n\mid a] = \dfrac 1 n\sum\limits_{i = 0} ^ {n - 1} \omega_n ^ {ia}\)。从判断式到和式的过程形成套路，深入了解其背后的逻辑有助于读者掌握并熟练运用这种套路。
莫比乌斯反演的结论：
- 若 \(g(n) = \sum\limits_{d\mid n} f(d)\)，则 \(f(n) = \sum\limits_{d\mid n} \mu(d) f\left(\dfrac n d\right)\)。即若 \(g = f * 1\)，则 \(f = g * \mu\)。
- 若 \(g(n) = \sum\limits_{n\mid d} f(d)\)，则 \(f(n) = \sum\limits_{n\mid d} \mu\left(\dfrac d n\right) g(d)\)。这其实就是上一节末尾提到的 \(\mu\) 作为容斥系数。验证：\(\sum\limits_{n\mid d} \mu\left(\dfrac d n\right) \sum\limits_{d\mid k} f(k) = \sum\limits_{n\mid k} f(k) \sum\limits_{d\mid \frac k n} \mu(d) = f(n)\)。
- 因为 \(\varphi * 1 = \mathrm{id}\)，所以 \(\mathrm{id} * \mu = \varphi\)，即 \(\sum\limits_{d \mid n} \dfrac n d \mu(d) = \varphi(n)\)。变式为 \(\sum\limits_{d\mid n} \dfrac{\mu(d)} d = \dfrac {\varphi(n)} n\)。
莫比乌斯反演的常见应用：
别看它只是将 \(\gcd(i, j)\) 带入 \(n\)，但这一步将 “\(i, j\) 互质” 这个条件转化为枚举 \(\gcd(i, j)\) 的约数 \(d\)，然后对 \(\mu(d)\) 求和。在 \(i, j\) 同样需要枚举的时候，可以先枚举 \(d\) 并计算合法的 \((i, j)\) 对数，这样 \(i, j\) 合法当且仅当 \(d\mid i\) 且 \(d\mid j\)，就把 \(i, j\) 独立开了。
5.4 常见技巧
相当于对 “最大公约数为 \(d\) 的倍数” 中的 \(d\) 做容斥：加上最大约数为 \(1\) 的倍数的对数，减去最大公约数为 \(p_i\) 的倍数的对数，加上最大公约数为 \(p_ip_j(i \neq j)\) 的倍数的对数，以此类推，得到每个 \(d\) 的贡献系数即莫比乌斯函数。
考虑单个质因子 \(p\)，再用中国剩余定理合并。设 \(a = v_p(i)\) 即 \(i\) 含质因子 \(p\) 的数量，\(b = v_p(j)\)，则 \(v_p(ij) = a + b\)。对于 \(ij\) 的约数 \(d\)，若 \(v_p(d) \leq a\)，则令其对应 \(v_p(x) = v_p(d)\)，\(v_p(y) = 0\)；若 \(v_p(d) > a\)，则令其对应 \(v_p(x) = 0\)，\(v_p(y) = v_p(d) - a\)。容易发现互质对 \((x, y)\) 和 \(d\) 之间形成双射，因此对 \(d\) 计数相当于对 \([x\perp y]\) 计数。例 XII.
5.5 例题
让我们在例题中感受莫比乌斯反演的广泛应用。除特殊说明，以下所有分式均向下取整。
I. P2522 [HAOI2011] Problem b
二维差分将和式下界化为 \(1\)，然后推式子：
只有 \(k\) 的倍数有用，将和式缩放 \(k\) 倍，得
莫比乌斯反演，得
枚举约数 \(d\)，记 \(c = \min\left(\dfrac n k, \dfrac m k\right)\)，
由于 \(1\sim x\) 中 \(y\) 的倍数有 \(\dfrac x y\) 个，故原式简化为
整除分块即可，时间复杂度 \(\mathcal{O}(n + T\sqrt n)\)，注意非必要不开 long long。代码。
II. SP5971 LCMSUM - LCM Sum
设 \(F(n)\) 表示 \(n\) 以内所有与 \(n\) 互质的数的和。当 \(n \geq 2\) 时，因为若 \(x\perp n\) 则 \(n - x\perp n\)，所以与 \(n\) 互质的数成对出现且和为 \(n\)。也就是说，每个与 \(n\) 互质的数对 \(F(n)\) 的平均贡献是 \(\dfrac n 2\)。因此 \(F(n) = \dfrac{n\varphi(n)} 2\)。
当 \(n = 1\) 时，\(F(1)\) 显然为 \(1\)。
另一种推导 \(F\) 的方式是莫比乌斯反演：
最后一步是因为 \(\mu * \mathrm{id} = \varphi\)，\(\mu * 1 = \epsilon\)。
答案为 \(n\sum\limits_{d\mid n} F(d)\)，化简为 \(\dfrac n 2 \left(1 + \sum\limits_{d\mid n} d \varphi(d)\right)\)。线性筛出 \(1 * (\mathrm{id} \times \varphi)\) 即可做到 \(\mathcal{O}(T + n)\)。代码。
III. P4318 完全平方数
设 \(f(n)\) 表示 \([1, n]\) 当中非完全平方数倍数的数的个数。二分答案，找到最小的 \(r\) 使得 \(f(r) \geq K\)，则 \(r\) 即为所求。
首先去掉 \(4, 9, \cdots, p ^ 2\) 的倍数，但同时是其中两个数的倍数的数会被算两次，所以加上 \((p_1p_2) ^ 2\) 的倍数，依次类推。相当于对 \(\mathbb N\) 做容斥，自然想到莫比乌斯函数。因此
直接计算，时间复杂度 \(\mathcal{O}(\sqrt n \log n)\)。代码。
IV. P2257 YY 的 GCD
注意到分母上的 \(pd \) 与两个变量相关，很麻烦。不妨设 \(T = pd\)，得
这一步调整了计算顺序使得可通过乘法分配律提出向下取整的式子。
另一种推导方式：考虑对 \([\gcd(i, j) = p]\) 容斥，然后对所有质数 \(p\) 求和，可知贡献系数 \(f\) 为所有容斥系数之和，即 \(f = \sum\limits_{p\in \mathbb P} \mu * \epsilon_p(n)\)。换句话说，\(f\) 等于将 \(\mu\) 的 下标 扩大质数倍后求和。我们发现 \(f(T) = \sum\limits_{p \mid T\land p\in \mathbb P} \mu\left(\dfrac T p\right)\)，与上式等价。
\(f\) 可以类似埃氏筛 \(n\log\log n\) 求出，因为每个位置仅与其所有质因子有关。将 \(f\) 前缀和后整除分块即可。时间复杂度 \(\mathcal{O}(T\sqrt n + n \log\log n)\)。
尽管 \(f\) 不是积性函数，但 \(f(T)\) 可以线性筛。具体方式留给读者自行推导，时间复杂度 \(\mathcal{O}(T\sqrt n+n)\)。代码。
V. P3455 [POI2007] ZAP-Queries
P2522 的子问题，代码。
VI. P2568 GCD
P2257 的子问题。
VII. P1829 [国家集训队] Crash 的数字表格
设 \(c = \min(n, m)\)。
根据 \(ij = \gcd(i, j) \times \mathrm{lcm}(i, j)\) 枚举 \(d = \gcd(i, j)\)，得
莫比乌斯反演，得
注意到后面两个和式不太好化简，我们设 \(S(T) = \sum\limits_{i = 1} ^ {\frac n T}\sum\limits_{j = 1} ^ \frac m T ij\)，并令 \(T = de\)，交换枚举顺序，得
至此已经可以狄利克雷前缀和 \(c\log \log c\) 求解问题。但注意到 \(\mu \cdot \mathrm{id}\) 是积性函数，所以 \(f = 1 * (\mu \cdot \mathrm{id})\) 也是积性函数，且其在质数幂处的取值可快速计算，可线性筛。则答案式化简为 \(\sum\limits_{i = 1} ^ c S(i)f(i)i\)，其中仅 \(S\) 与 \(n, m\) 有关。同时注意到 \(S\) 仅涉及到 \(n, m\) 整除值处的等差数列求和，因此求出 \(f(i) i\) 的前缀和后，可整除分块 \(\mathrm{O}(\sqrt c)\) 求解答案。
时间复杂度 \(\mathcal{O}(c + T\sqrt c)\)。代码。
VIII. AT5200 [AGC038C] LCMs
令 \(S = \sum\limits_{i = 1} ^ N \sum\limits_{j = 1} ^ N \mathrm{lcm}(A_i, A_j)\)，则答案为 \(S\) 减去 \(A\) 的和之后除以 \(2\)。问题转化为求 \(S\)。
设 \(c_i\) 表示 \(i\) 在 \(A\) 中的出现次数，即 \(c_i = \sum\limits_{j = 1} ^ N [A_j = i]\)，则
其中 \(T = dd'\)，\(f(T) = \sum\limits_{d\mid T} \mu(d) d\)，\(g(T) = \sum\limits_{i = 1} ^ {\frac V T} ic_{iT}\)。\(f\) 容易线性筛预处理，\(g\) 可以枚举因数或狄利克雷后缀和。时间复杂度 \(\mathcal{O}(V\log V)\) 或 \(\mathcal{O}(V\log\log V)\)。代码。
IX. P3911 最小公倍数之和
双倍经验。
X. P6156 简单题
和上题一样的套路。枚举 \(\gcd\)，再莫比乌斯反演，得
令 \(T = dd'\)，得
线性筛预处理出 \(f = (d\times \mu ^ 2) * \mu\) 的前缀和，并预处理自然数幂和求后面的东西。整除分块求解上式，时间复杂度 \(\mathcal{O}(n\frac {\log k}{\log n})\)。代码见下一题。
XI. P6222 「P6156 简单题」加强版
双倍经验，时间复杂度 \(\mathcal{O}(n\frac {\log k}{\log n} + T\sqrt n)\)。注意比较卡空间。代码。
XII. P3327 [SDOI2015] 约数个数和
利用 5.4 小节的第二个公式，套入莫比乌斯反演，可得答案式
整除分块预处理 \(g(n) = \sum\limits_{i = 1} ^ n \dfrac n i\)，则答案为 \(\sum\limits_{d = 1} ^ {\min(n, m)} \mu(d) g(\frac n d) g(\frac m d)\)，整除分块即可。时间复杂度 \(\mathcal{O}((n + T)\sqrt n)\)。代码。
XIII. P1447 [NOI2010] 能量采集
XIV. P6810 「MCOI-02」Convex Hull 凸包
XV. P2158 [SDOI2008] 仪仗队
XVI. P3704 [SDOI2017] 数字表格
设 \(c = \min(n, m)\)。
线性或线对预处理 \(f\) 及其逆元，线对预处理 \(g(n) = \sum\limits_{d\mid n} f_d ^ {\mu(\frac n d)}\)。对每组询问整除分块即可做到 \(\mathcal{O}(T\sqrt n\log n)\)。
6. 杜教筛
杜教筛可以在亚线性时间内求出满足条件的数论函数前缀和。
6.1 算法介绍
杜教筛公式的推导相当自然，但动机十分巧妙。设希望求出 \(f\) 在 \(n\) 处的前缀和 \(s(n) = \sum\limits_{i = 1} ^ n f(i)\)，我们构造另一个数论函数 \(g\)，设 \(h = f * g\)，则
这说明若 \(g, h\) 的前缀和可快速求出，我们就得到了 \(s(n)\) 关于其所有整除值处取值的递推式，即
一般可杜教筛函数 \(f\) 及其对应构造函数 \(g\) 均为积性函数，因此 \(g(1) = 1\)，公式又写为。
另一种理解方式：设第一象限每个整点 \((x, y)\) 的权值为 \(f(y) g(x)\)。想象反比例函数 \(y = \dfrac n x\)，它与 \(x, y\) 轴正半轴围成的区域内所有整点的权值和为 \(S = \sum\limits_{xy\leq n} f(y)g(x)\)。当 \(x = 1\) 时，\(\sum\limits_{y = 1} ^ n f(y)\) 即 \(s(n)\) 贡献至 \(S\)。当 \(x > 1\) 时，考虑一个横坐标区间 \([L, R](2\leq L\leq R\leq n)\)。若对于任意 \(x\in [L, R]\) 满足 \(\left\lfloor\dfrac n x\right\rfloor\) 相等，即 \(\left\lfloor\dfrac n L\right\rfloor = \left\lfloor\dfrac n R\right\rfloor\)，则该横坐标区间所有产生贡献的点形成矩形 \([L, R] \times \left[1, \left\lfloor\dfrac n L\right\rfloor\right]\)，它们的权值和即 \(\left(\sum\limits_{x = L} ^ R g(x) \right) s\left(\dfrac n L\right)\)。由于整除值数量为 \(\mathcal{O}(\sqrt n)\)，所以 \(S\) 可写为 \(\mathcal{O}(\sqrt n)\) 个矩形的和。稍作变形即得 \(s(n)\) 的递推式。
复杂度分析：由递推式可知求解 \(s(n)\) 的复杂度为 \(n\) 的所有整除值的根号和。考虑 \(> \sqrt n\) 的整除值的贡献，即 \(\sum\limits_{d = 1} ^ {\sqrt n} \sqrt {\frac n d}\)。\(\int \sqrt{n} x ^ {-\frac 1 2} dx = 2\sqrt n x ^ {\frac 1 2}\)，将 \(x = \sqrt n\) 带入，得 \(2n ^ {\frac 3 4}\)。而小于 \(\sqrt n\) 的整除值的贡献为 \(\sum\limits_{d = 1} ^ {\sqrt n} \sqrt d\)。\(\int \sqrt x dx = \frac 2 3 x ^ {\frac 3 2}\)，将 \(x = \sqrt n\) 带入，得 \(\frac 2 3 n ^ {\frac 3 4}\)。因此总复杂度为 \(\mathcal{O}(n ^ {\frac 3 4})\)。
在复杂度分析过程中我们还得到了一个有趣的结论：大于 \(\sqrt n\) 和小于 \(\sqrt n\) 的整除值的根号和级别相等。对于笔者而言，这个结论出乎意料。
一般预处理 \(f\) 及其前缀和到 \(n ^ {\frac 2 3}\) 处，复杂度优化为 \(n ^ {\frac 2 3} + \sqrt n (n ^ {\frac 1 3}) ^ {\frac 1 2} = \mathcal{O}(n ^ {\frac 2 3})\)。
6.2 例题
I. P4213 【模板】杜教筛（Sum）
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int N = 5e6 + 5;
bool vis[N];
int cnt, pr[N], mu[N], phi[N], smu[N];
ll sphi[N];
unordered_map<int, ll> p, m;
ll dp(int n) {
if(n < N) return sphi[n];
auto it = p.find(n);
if(it != p.end()) return it->second;
ll sum = 1ll * n * (n + 1ll) / 2;
for(int l = 2, r; ; l = r + 1) {
r = n / (n / l);
sum -= (r - l + 1) * dp(n / l);
if(r == n) break;
}
return p[n] = sum;
}
int dm(int n) {
if(n < N) return smu[n];
auto it = m.find(n);
if(it != m.end()) return it->second;
ll sum = 1;
for(int l = 2, r; l <= n; l = r + 1) {
r = n / (n / l);
sum -= (r - l + 1) * dm(n / l);
if(r == n) break;
}
return m[n] = sum;
}
int main() {
mu[1] = phi[1] = 1;
for(int i = 2; i < N; i++) {
if(!vis[i]) pr[++cnt] = i, mu[i] = -1, phi[i] = i - 1;
for(int j = 1; j <= cnt && i * pr[j] < N; j++) {
vis[i * pr[j]] = 1;
if(i % pr[j] == 0) {
phi[i * pr[j]] = phi[i] * pr[j];
break;
}
phi[i * pr[j]] = phi[i] * (pr[j] - 1);
mu[i * pr[j]] = -mu[i];
}
}
for(int i = 1; i < N; i++) smu[i] = smu[i - 1] + mu[i], sphi[i] = sphi[i - 1] + phi[i];
int T, n;
cin >> T;
while(T--) {
cin >> n;
cout << dp(n) << " " << dm(n) << "\n";
}
return 0;
}
参考文章
第一章：
第三章：
第六章：
