高级图论

本篇博客已经弃用。最新修订版见 图论 II。

初级图论。

CHANGE LOG

• 2022.5.26：修改文章。
• 2022.6.8：添加 SAT 的定义。
• 2022.6.10：添加 DAG 的支配树。
• 2022.9.30：添加 DAG 链剖分。

1. 同余最短路

说难也不算难，但是挺有意思的一个知识点。应用不广泛。

前置知识：SPFA / Dijkstra 求最短路。

1.1 算法简介

同余最短路用于求解在某个范围内有多少重量可以由若干物品做完全背包凑出，或者说，有多少数值可由给定的一些数进行 系数非负 的线性组合得到。

我们尝试具体描述这样的问题。给出 $n(n\le 50)$ 个数 $a_i(1\le a_i\le {10}^5)$，求 $[L,R](1\le L\le R\le {10}^{18})$ 以内满足能表示成 $\sum _{c_i\ge 0}{a}_i{c}_i$ 的正整数个数。

同余最短路的核心思想在于观察到：如果一个数 $r$ 可以被表出，那么任何 $r+x{a}_i(x>0)$ 也可以被表出。因此只需选出任意一个 $a_i$，求出每个模 $a_i$ 同余的同余类 $K_j$ 当中最小的能被表出的数 $f_j$，即可快速判断一个数 $S$ 能否被表出：当且仅当 $S\ge f(Smod{a}_i)$。

这个思想非常巧妙，感觉不是凡人能够想到的思路。一种可能的理解方式是，考虑每个数能否被表出的状态 $g(r)$，我们发现对于某个 $a_i$，如果 $r_1\equiv r_2(\mathrm{mod}{a}_i)$ 且 $r_1<r_2$，那么必然有 $g(r_1)\le g(r_2)$。这样一来，根据单调性下的定义域值域互换的技巧，设 $f_j$ 表示使得 $g(r)=1$ 且 $rmod{a}_i=j$ 的最小的 $r$。

$a$ 本身很小，所以对每个同余类求出最小数是可行的。为了减小常数，我们一般会选择使得同余类个数最少的 $a_i$，即 $a$ 的最小值。不妨设其为 $a_1$。

得到模 $a_1$ 余 $j$ 的数中最小的能被表示出来的数 $f_j$ 后，可以通过加上 $a_2\sim a_n$ 转移到其它同余类 $f_k(k\equiv j+a_i(\mathrm{mod}{a}_1))$。

注意到上述过程非常像一个最短路：对于每个点 $j$，它向 $(j+a_i)mod{a}_1$ 连了一条长度为 $a_i$ 的边，需要求从源点 $0$ 开始到每个点的最短路。使用 dijkstra 或 SPFA 求解。

初始值 $f_0=0$，$f_i=+\mathrm{\infty }(1\le i<a_1)$。

求出 $f_j$ 后得到答案是容易的。首先进行一步差分转化为求 $[0,R]$ 有多少个数能被表出，此时答案为

$$\sum _{i=0}^{a_1-1}max(0,\lfloor {\displaystyle \frac{R-f_i}{a_1}}\rfloor +1)$$

用 $[0,R]$ 的答案减去 $[0,L-1]$ 的答案即可。

时间复杂度为 dijkstra 的 $\mathcal{O}(n{a}_1\log a_1)$ 或 SPFA 的 $\mathcal{O}(n{a}_{1}k)$。SPFA 跑不满，因为图的形态和边权相对固定，不会出现把 SPFA 卡死的情况，所以一般比 dijkstra 快。代码见例 I.

1.2 例题

*I. P2371 [国家集训队] 墨墨的等式

同余最短路模板题。

设 $m=n\times a_i$。使用 $\mathcal{O}(mk)$ 的 SPFA 会比 $\mathcal{O}(m\log m)$ 的 dijkstra 快不少。

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n, a[N], in[N];
long long f[N], l, r, ans;
int main() {
  cin >> n >> l >> r;
  for(int i = 1; i <= n; i++) cin >> a[i];
  memset(f, 0x3f, sizeof(f));
  sort(a + 1, a + n + 1);
  queue<int> q;
  q.push(0), f[0] = 0;
  while(!q.empty()) {
    int t = q.front();
    q.pop(), in[t] = 0;
    for(int i = 2; i <= n; i++) {
      int it = (t + a[i]) % a[1];
      long long d = f[t] + a[i];
      if(d < f[it]) {
        f[it] = d;
        if(!in[it]) in[it] = 1, q.push(it);
      }
    }
  }
  for(int i = 0; i < a[1]; i++) {
    if(r >= f[i]) ans += max(0ll, (r - f[i]) / a[1] + 1);
    if(l > f[i]) ans -= max(0ll, (l - 1 - f[i]) / a[1] + 1);
  }
  cout << ans << endl;
  return cerr << "Time: " << clock() << endl, 0;
}

II. P3403 跳楼机

同余最短路的板子题。

*III. AT3621 [ARC084B] Small Multiple

一道神仙题。

注意到所有数都可以从 $1$ 开始经过若干次 $+1$ 或 $\times 10$ 得到，因此每个点 $i$ 向 $(i+1)modK$ 连一条权值为 $1$ 的边，向 $10imodn$ 连一条权值为 $0$ 的边，跑 01 BFS 即可。

注意，不可以以 $0$ 作为源点，因为题目要求倍数是正整数，且我们希望求的就是 $f_0$，所以 $0$ 不能算。对于本题而言，$f_i$ 定义为模 $K$ 等于 $i$ 的 正整数 的各位数字之和的最小值。

时间复杂度 $\mathcal{O}(K)$，代码。写了 SPFA，跑得也很快。

IV. P2662 牛场围栏

同余最短路板题。

SPFA 的时间复杂度为 $\mathcal{O}(L^{2}k)$，比 dijkstra 的 $\mathcal{O}(L^2\log L)$ 跑得快一些。

V. 模拟赛题 梦回 2021

给定 $n$ 个值域 $[2,m]$ 的 随机数，求最大的不能被这些数表示出的数。$50\le n\le {10}^7$，$2\le m\le {10}^8$。

和 IV. 一样，无限背包问题考虑同余最短路。因为数据随机，所以最小值的期望为 ${\displaystyle \frac{m}{n+1}}$。

直接跑 SPFA 的期望复杂度为 $\mathcal{O}(\frac{m}{n+1}\times nk)\approx \mathcal{O}(mk)$，可以通过。

[P4156 WC2016]论战捆竹竿 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

2. 2-SAT

2-SAT 具有很强的逻辑性，因为 SAT 本身由逻辑学术语定义。

2.1 SAT 的定义

该部分与 OI 没有太大关系，不感兴趣的读者可以跳过。

为方便说明，首先给出相关术语。

• 合取：用符号 $\wedge$ 表示，是自然语言联结词 “且” 的抽象。命题 $p\wedge q$ 表示 $p,q$ 的合取，称为合取式，读作 $p$ 且 $q$，其为真当且仅当 $p,q$ 均为真。简单地说，合取就是逻辑与 &&，可以类比计算机科学中的按位与 &，相信这个概念大家并不陌生。
• 析取：用符号 $\vee$ 表示，是自然语言联结词 “或” 的抽象。命题 $p\vee q$ 表示 $p,q$ 的析取，称为析取式，读作 $p$ 或 $q$，其为真当且仅当 $p,q$ 至少有一个为真。同样的，合取是逻辑或 ||，类比按位或 |。
• 否定：用符号 $\mathrm{\neg }$ 表示，$\mathrm{\neg }p$ 表示命题 $p$ 的否定，其真假性与 $p$ 相反。否定是逻辑非 !，类比按位取反 ~。

上述三条概念均为基本命题联结词，大概可以看作给常见的 “与或非” 三种运算起了高大上的名字。将命题变元（可真可假的布尔变量）用合取 $\wedge$，析取 $\vee$ 和否定 $\mathrm{\neg }$ 联结在一起，得到布尔逻辑式（叫法不唯一）。

布尔逻辑式可满足，指存在一个对所有命题变元的真假赋值，使得该布尔逻辑式为真。

布尔可满足性问题（Boolean Satisfiability Problem）简称 SAT，它定义为检查一个布尔逻辑式是否可满足，是第一个被证明的 NPC 问题。

• 命题变元或其否定称为文字。
• 若干个文字的析取称为简单析取式，形如 $P=x_1\vee x_2\vee \cdots \vee x_k$，其中 $x_i$ 表示命题 $p_i$ 或其否定 $\mathrm{\neg }{p}_i$。
• 若干简单析取式的合取称为合取范式（Conjunctive Normal Form，CNF），形如 $P_1\wedge P_2\wedge \cdots \wedge P_n$，其中 $P_i$ 表示一个简单析取式。

考虑 SAT 的简单版本：命题公式为合取范式，且组成它的每个简单析取式至多含有 $k$ 个文字。这一问题称为 k-SAT。

当 $k\ge 3$ 时 k-SAT 是 NPC 问题，但 2-SAT 存在多项式复杂度的解法。接下来介绍这一算法。

2.2 算法介绍

首先我们将抽象的 2-SAT 描述得更具体一些。将简单析取式看成条件，我们希望每个条件均被满足，而每个简单析取式的形态是固定的：$p_i$，$\mathrm{\neg }{p}_i$，$p_i\vee p_j$，$p_i\vee \mathrm{\neg }{p}_j$，$\mathrm{\neg }{p}_i\vee \mathrm{\neg }{p}_j(i\ne j)$。

注意到每个条件仅和至多两个文字（变量）有关，这启发我们思考图论解法。

尝试将限制写成 “若，则” 的形式，因为可达性具有传递性，而蕴含性同样具有传递性（若 $A$ 则 $B$，若 $B$ 则 $C$，说明若 $A$ 则 $C$）。根据这些限制，我们可以建出一张有向图，它自然地表示出了当每个文字为真时，有哪些文字必须为真。

• $p_i$：$p_i$ 必须为真。可以用若 $\mathrm{\neg }{p}_i$ 则 $p_i$ 来限制 $p_i$ 为真。
• $\mathrm{\neg }{p}_i$：$p_i$ 必须为假。同理，若 $p_i$ 则 $\mathrm{\neg }{p}_i$。
• $p_i\vee p_j(i\ne j)$：$p_i$ 和 $p_j$ 不能同时为假，即若 $\mathrm{\neg }{p}_i$ 则 $p_j$，若 $\mathrm{\neg }{p}_j$ 则 $p_i$。
• $p_i\vee \mathrm{\neg }{p}_j$：若 $\mathrm{\neg }{p}_i$ 则 $\mathrm{\neg }{p}_j$，若 $p_j$ 则 $p_i$。
• $\mathrm{\neg }{p}_i\vee \mathrm{\neg }{p}_j$：若 $p_i$ 则 $\mathrm{\neg }{p}_j$，若 $p_j$ 则 $\mathrm{\neg }{p}_i$。

注意第三，四，五中简单析取式所产生的连边具有 对称性。因为若一个命题成立，则其逆否命题仍然成立：若 $A\Rightarrow B$，则 $\mathrm{\neg }B\Rightarrow \mathrm{\neg }A$。

这样，若一个命题变元 $p_i$ 为真可推导出它的否定为真，即 $p_i⇝\mathrm{\neg }{p}_i$，则该命题变元必须为假。反之亦然。进一步地，若 $p_i$ 和 $\mathrm{\neg }{p}_i$ 强连通，则 2-SAT 无解。

因此，对有向图进行强连通分量缩点，若 $p_i$ 和 $\mathrm{\neg }{p}_i$ 在同一强连通分量说明 $p_i$ 非真非假，矛盾，问题无解。

除此以外，是否一定有解呢？

首先确定解的形态。对于与命题变元 $p_i$ 相关的两个文字 $p_i$ 和 $\mathrm{\neg }{p}_i$，有且仅有一个文字为真，恰对应命题变元 $p_i$ 为真或假。所有选出为真的共 $n$ 个文字（若一个命题变元为假，则它的否定对应的文字为真）对应的点集 $P$ 在有向图上的闭合子图（即所有这些点能到达的点构成的点导出子图）不同时包含一个命题变元及其否定。这说明闭合子图内部恰有 $n$ 个点，继而得到 $P$ 的点导出子图等于其闭合子图，等价表述是不存在一个为假的文字被一个为真的文字到达。

接下来尝试构造一组解。注意到若 $\mathrm{\neg }{p}_i⇝p_i$，则 $p_i$ 的拓扑序一定大于 $\mathrm{\neg }{p}_i$，所以对每个命题变元及其否定，最直接的想法是选择拓扑序更大的那一个。

先猜后证，考虑证明这样做的正确性。反证法，假设存在 $p_i$ 和 $p_j$，满足 $p_i$ 的拓扑序大于 $\mathrm{\neg }{p}_i$，$p_j$ 的拓扑序大于 $\mathrm{\neg }{p}_j$，但是 $p_i$ 可达 $\mathrm{\neg }{p}_j$。根据命题与其逆否命题的等价性，$p_j$ 可达 $\mathrm{\neg }{p}_i$。因为 $p_i$ 的拓扑序大于 $\mathrm{\neg }{p}_i$，所以 $p_j$ 的拓扑序小于 $\mathrm{\neg }{p}_i$ 小于 $p_i$。因为 $p_j$ 的拓扑序大于 $\mathrm{\neg }{p}_j$，所以 $p_i$ 的拓扑序小于 $\mathrm{\neg }{p}_j$ 小于 $p_j$，矛盾。

因此此时一定有解。

综上，若只需求出任意一组解，那么对所点后的图拓扑排序，然后对于每个命题变元相关的两个文字，使得拓扑序更大的那个为真。注意到我们在 tarjan 时已经得到了缩点后 DAG 的反向拓扑序：若 $u⇝v$，则 $v$ 在 $u$ 之前被弹出，即 col[v] <= col[u]，因此只需选择 col 较小的文字赋为真。时间复杂度 $\mathcal{O}(n+m)$，其中 $n$ 是命题变元数量，$m$ 是简单析取式数量。

如果要求字典序最小解，可以按位贪心，每次尽量选字典序小的点，遍历所有其能够到达的点并检查是否使当前决策出现矛盾，贪心的局部决策不影响全局合法性留给读者自证。时间复杂度 $\mathcal{O}(n(n+m))$。Bitset 优化求传递闭包可做到 $\mathcal{O}\left({\displaystyle \frac{n^3}{w}}\right)$。

2.3 例题

P4782 【模板】2-SAT 问题

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e6 + 5; // 两倍空间
int cnt, hd[N], nxt[N], to[N];
void add(int u, int v) {nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v;}
int n, m, dn, dfn[N], low[N], top, stc[N], vis[N], cn, col[N];
void tarjan(int id) {
  dfn[id] = low[id] = ++dn, vis[id] = 1, stc[++top] = id;
  for(int i = hd[id]; i; i = nxt[i]) {
    int it = to[i];
    if(!dfn[it]) tarjan(it), low[id] = min(low[id], low[it]);
    else if(vis[it]) low[id] = min(low[id], dfn[it]);
  }
  if(low[id] == dfn[id]) {
    col[id] = ++cn;
    while(stc[top] != id) col[stc[top]] = cn, vis[stc[top--]] = 0;
    vis[id] = 0, top--;
  }
}
int main() {
  cin >> n >> m;
  for(int i = 1; i <= m; i++) {
    int u, a, v, b;
    scanf("%d%d%d%d", &u, &a, &v, &b);
    add(u + (!a) * n, v + b * n); // 当 u 等于 !a 时，v 必须等于 b
    add(v + (!b) * n, u + a * n); // 同理
  }
  for(int i = 1; i <= n << 1; i++) if(!dfn[i]) tarjan(i);
  for(int i = 1; i <= n; i++) if(col[i] == col[i + n]) puts("IMPOSSIBLE"), exit(0);
  puts("POSSIBLE");
  for(int i = 1; i <= n; i++) putchar('0' + (col[i + n] < col[i])), putchar(' '); // 选 col 更小的
  return 0;
}

P3825 [NOI2017] 游戏

若没有 x 就是裸的 2-SAT。

注意到 $d$ 非常小，所以 $2^d$ 枚举每个 x 的状态：a 或 c，这保证了任何一种合法解都被考虑到。

时间复杂度 $\mathcal{O}(2^d(n+m))$。代码。

*P6965 [NEERC2016] Binary Code

一个字符串至多含有一个问号，所以状态至多有两种，考虑 2-SAT，设 $x_i$ 表示第 $i$ 个字符串的问号填 $0$，$\mathrm{\neg }{x}_i$ 表示第 $i$ 个字符串的问号填 $1$。现在我们有 $2n$ 个字符串和 $2n$ 个文字，它们之间一一对应。

容易发现，若字符串 $s$ 是 $t$ 的前缀，则若 $s$ 对应文字为真，则 $t$ 对应文字为假；若 $t$ 对应文字为真，则 $s$ 对应文字为假。这说明若 $s$ 则非 $t$，若 $t$ 则非 $s$。

刻画前缀关系的结构是字典树。对于若 $s$ 则非 $t$ 的限制，我们需要从 $s$ 向它的子树内所有字符串的 否定 连边。对于若 $t$ 则非 $s$ 的限制，我们需要从 $t$ 向它的祖先对应的所有字符串的 否定 连边。因此，建出根向字典树和叶向字典树。在两棵字典树上，每个字符串对应的状态向它对应文字的否定连边。为防止出现 $s$ 和 $t$ 对应同一字符串的情况，在叶向字典树上，$s$ 对应文字只能向它对应状态的两个儿子连边，否则 $s$ 会向 $s$ 的否定连边，导致必然无解。同理，在根向字典树上，$s$ 对应文字向它对应节点的父亲（而非它本身）连边。

我们还要处理 $s=t$ 但对应不同字符串的情况。容易发现，将相等的字符串排成一行，每个字符串会向所有除了它本身的其它字符串的 否定 连边，可以通过前缀后缀优化建图做到。

综上，点数和边数关于 $n$ 和字典树大小 $m$ 线性。点数不超过 $4n+2m$，而 $m\le 2n$，所以点数不超过 $8n$。代码。

3. 广义圆方树

前置知识：tarjan 求割点和边双的缩点的正确性证明（懒得再证一遍正确性了），详见 初级图论。

广义圆方树是刻画图上点的必经性的强力工具。它可以描述原图任意两点之间的所有割点，即 $u\to v$ 的所有必经点。

点双和边双的缩点方法类似，都是借助 tarjan 算法求出所有连通分量的具体形态。但是它们缩点后得到的结构形态却截然不同。这是因为一个节点最多只会出现在一个边双当中（相对应的，一条边最多属于一个点双），所以边双缩点时可以将一个边双内部所有点看成一个点。但是一个点可能出现在若干点双当中，而且为了刻画必经点，我们希望在缩点时保留这些割点（边双缩点时也保留了割边对吧）。

3.1 点双相关性质

咕咕咕，可以看例题 V. 题解，有时间再补充在这里。

3.2 算法介绍

广义圆方树是定义在 一般无向图 上的一种树型结构。它是点双缩点后的产物，可以有效解决必经性相关的题目。

点双的缩点本质上可以看成 “缩边”，就是把原图上所有对刻画必经性无用的边全部丢掉。

考察一个点双。如果我们希望将它缩成一棵树，并且树上任意两点之间的简单路径恰包含且仅包含它们之间的必经点，那么任意两点之间都必须直接相连，因为单独考察一个点双，其内部不存在必经点。但这和 “缩成一棵树” 矛盾。

为此，我们尝试建出点双的 “代表点” 并向点双内部所有点连边。容易发现这样一种菊花满足条件，因为任意两点通过中心点间接地直接相连。

这样就可以自然地引出圆方树的定义了：将原图的点视为圆点。对于原图中的每一个点双，新建 代表该点双 的方点连向点双内部所有圆点。

每个点双缩成一张菊花图，多个菊花图通过原图中的割点相连，因为 点双的分隔点是割点。类比边双缩点时，每个边双缩成一个点，多个点通过原图中的割边相连。

广义圆方树的建法只需在 tarjan 算法的基础上稍作修改即可。节点 $v$ dfs 完毕回溯到其父节点 $u$ 时，若 low[v] >= dfn[u]（回忆割点的判定法则），说明 $v$ 及其子树在栈内（也是栈顶）的部分与 $u$ 共同形成了一个点双。新建代表点双的方点并对应连边，弹出栈顶直到 $v$ 被弹出即可。注意这里 不能弹出 $u$，因为 $u$ 可能和它别的儿子形成另外的点双（但 $v$ 不会了，因为 $v$ 及其子树已经被处理掉了）。

正确性（弹出点集形成的连通分量的唯一性和极大性）可以类似边双缩点证，这里不再赘述。以下是一些注意点。

• 当原图不连通时，每个连通块处理完之后栈内会剩下一个点，即进入该连通块的点。
• 每个点双均会新建一个方点，所以需要开两倍空间存储圆方树。当图是一张菊花时，点双数量为 $n-1$。

广义圆方树提供了原图上所有割点的信息，是解决必经性问题的得力助手，也是很有用的一类树形结构。代码见例题 I.

3.3 性质

我们先给出一些与点双连通性相关的引理：

引理 1：除了 $x,y$ 本身，$x,y$ 在原图上的必经点为割点。

证明：考虑一个不等于 $x$ 或 $y$ 的非割点，删去后整张图仍然连通。

引理 2：$z$ 是 $x,y$ 的必经点当且仅当删去 $z$ 后 $x,y$ 不连通。

证明：若删去 $z$ 后 $x,y$ 连通说明存在不经过 $z$ 的连接 $x,y$ 的简单路径；假设存在连接 $x,y$ 的简单路径不经过 $z$，那么删去 $z$ 后 $x,y$ 可以通过该简单路径连通。因此，$z$ 不是 $x,y$ 的必经点当且仅当删去 $z$ 后 $x,y$ 连通，原命题继而得证。

引理 3：若 $x$ 与 $y,z$ 均点双连通，但 $y,z$ 不点双连通，则 $x$ 是 $y,z$ 的必经点。

证明：考虑 $y\to x$ 的两条仅在端点处相交的路径 $P_1,P_2$ 以及 $x\to z$ 的两条仅在端点处相交的路径 $P_3,P_4$。$P_1\to P_3$ 和 $P_2\to P_4$ 使得 $y,z$ 之间只有 $x$ 可能是必经点，再根据 $y,z$ 不点双连通得证。

上述引理容易感性理解，读者应当认为它们的成立非常自然。

接下来是一些由浅到深，层层递进的圆方树相关性质，最重要且常见的性质在最后给出。

性质 1：圆点 $x$ 的度数等于包含它的点双个数。

证明：根据圆方树的构建方式，显然。

性质 2：圆方树上圆方点相间。

证明：任何两个在同一点双内的点由该点双对应的方点间接相连。

性质 3：原图上直接相连的 $x,y$ 包含于同一点双。

证明：$x,y$ 点双连通。

性质 4：圆点 $x$ 是叶子当且仅当它在原图上是非割点。

证明：

若 $x$ 是割点，则删去 $x$ 后存在与 $x$ 直接相邻的两点 $y,z$ 不连通（显然），所以 $x,y,z$ 不包含于同一点双 $S$，又因为 $x,y$ 点双连通，$x,z$ 点双连通，所以 $x$ 至少包含于两个点双。

若 $x$ 至少包含于两个点双，则根据性质 2，存在 $y,z$ 使得 $x,y$ 点双连通，$x,z$ 点双连通，但 $y,z$ 不点双连通，根据引理 3，$x$ 是 $y,z$ 的必经点，即 $x$ 是割点，得证。

性质 5：在广义圆方树上删去圆点 $x$ 后剩余节点的连通性与在原图上删去 $x$ 相等。

证明：因为删去 $x$ 时只删去 $x$ 的邻边，所以只需证明与 $x$ 直接相邻的任意两点 $y,z$ 连通性相等。

若 $x,y,z$ 在同一点双，则据点双定义原图删去 $x$ 后 $y,z$ 连通，同时圆方树上删去 $x$ 后 $y,z$ 通过方点连通。

若 $x,y$ 和 $x,z$ 在不同点双 $S_1,S_2$，据引理 3 原图删去 $x$ 后 $y,z$ 不连通，同时圆方树上删去 $x$ 后方点 $S_1$ 和方点 $S_2$ 不连通（$x$ 和 $S_1,S_2$ 直接相连，且圆方树的形态是树），得出圆方树上删去 $x$ 后 $y,z$ 不连通，得证。

性质 6：$x,y$ 简单路径上的所有圆点恰好是原图 $x,y$ 之间的所有必经点。

证明：若圆点 $z$ 在圆方树上 $x,y$ 的简单路径上，则圆方树上删去 $z$ 后 $x,y$ 不连通，根据性质 6 原图删去 $z$ 后 $x,y$ 不连通，根据引理 2 $z$ 是 $x,y$ 的必经点。反之可证 $z$ 不是 $x,y$ 的必经点，得证。

总结一下，这些性质无非就是在描述一个核心结论：若在圆方树上 $z$ 是 $x,y$ 的必经点，则原图 $z$ 是 $x,y$ 的必经点。换言之，圆方树完整地保留了原图的必经性。

3.4 例题

I. P5058 [ZJOI2004] 嗅探器

对原图建出广义圆方树，那么 $a,b$ 两点之间的所有圆点（也是割点）的编号最小值即为所求。注意不能包含 $a,b$ 本身。

如果不存在这样的圆点则无解，此时 $a,b$ 处在同一点双内部。

时间复杂度 $\mathcal{O}(n+m)$。

#include <bits/stdc++.h>
using namespace std;
const int N = 4e5 + 5;
int n, a, b, node;
int dn, dfn[N], low[N], top, stc[N];
vector<int> e[N], g[N];
void tarjan(int id) {
  dfn[id] = low[id] = ++dn, stc[++top] = id;
  for(int it : e[id]) {
    if(!dfn[it]) {
      tarjan(it), low[id] = min(low[id], low[it]);
      if(low[it] == dfn[id]) {
        g[++node].push_back(id), g[id].push_back(node);
        for(int x = 0; x != it; )
          g[node].push_back(x = stc[top--]), g[x].push_back(node);
      }
    }
    else low[id] = min(low[id], dfn[it]);
  }
}
int fa[N], dep[N];
void dfs(int id, int ff) {
  fa[id] = ff, dep[id] = dep[ff] + 1;
  for(int it : g[id]) if(it != ff) dfs(it, id);
}
int main() {
  cin >> n, node = n;
  scanf("%d%d", &a, &b);
  while(a && b) {
    e[a].push_back(b), e[b].push_back(a);
    scanf("%d%d", &a, &b);
  }
  tarjan(1), dfs(1, 0);
  scanf("%d%d", &a, &b);
  int ans = N;
  if(dep[a] < dep[b]) swap(a, b);
  while(dep[a] > dep[b]) if((a = fa[a]) != b) ans = min(ans, a);
  while(a != b) ans = min(ans, min(a = fa[a], b = fa[b]));
  if(ans > n) puts("No solution");
  else cout << ans << "\n";
  return 0;
}

II. P4630 [APIO2018] Duathlon 铁人两项

广义圆方树基础练习题。

首先进行一步转化，对所有点对 $(u,v)$ 求它们之间简单路径的并去掉 $u,v$ 之后的点集大小之和。

由于本题简单路径定义为不经过重复点的路径，且题目考察连通性相关，不难想到建出广义圆方树。因此相当于求 $(u,v)$ 之间所有方点所表示的点双大小之和。

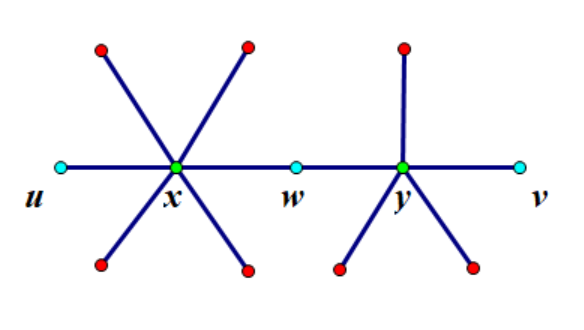
注意，路径上每个除了 $u,v$ 以外的割点会被算到两次，而 $u,v$ 本身也会被路径上它们所在的点双算入一次。这说明路径上每个圆点都被多算了一次。因此，每个方点的贡献是其对应的点双大小，而每个圆点的贡献是 $-1$。

如上图，从最左边的 $u$ 到最右边的 $v$，路径上共有两个方点 $x,y$。单纯将它们的权值加起来会得到 $6+5=11$。但我们发现正确的答案应该是 $8$，因为只有所有红点和 $w$ 才会作为中转点。错误原因是 $u,v,w$ 均被多算了一次，真正的答案应由 $-1+6-1+5-1$ 求得。

设每个点的权值为 $a$，问题等价于求 $\sum _{u\ne v\wedge u,v\le n}\sum _{p\in \mathrm{path}(u,v)}{a}_p$。一般而言，我们用大于 $n$ 的数值给方点标号（具体见上一题代码），所以有限制 $u,v\le n$。

转换贡献方式，考察圆方树上每个节点对答案的贡献。容易通过一遍 dfs 求出子树大小的同时求解该问题。

注意原图可能不连通。

时间复杂度线性。代码。

III. P4606 [SDOI2018] 战略游戏

扣掉一个节点后 $u$ 不能到达 $v$，说明该节点是 $u,v$ 之间的割点。因此，建出广义圆方树，我们发现题目相当于求点集 $S$ 在树上的虚树所包含的不属于 $S$ 的圆点数量。

对每个点是否为圆点做树上前缀和，虚树上一条边的贡献（不含两端）容易计算。再加上所有不在 $S$ 内部但是是圆点的虚树节点的贡献，时间复杂度线性对数。

代码。

IV. P4334 [COI2007] Policija

建出广义圆方树。

对于类型 2 的询问，直接判 $C$ 是否在 $A,B$ 的简单路径上。

对于类型 1 的询问，首先判 $(G_1,G_2)$ 是否为割边（即点双大小为 $2$），若是，则判 $G_1\to C(G_1,G_2)\to G_2$ 这条路径是否在 $A,B$ 的简单路径上，其中 $C(G_1,G_2)$ 是这两个点形成的方点。因为点双大小为 2，所以该方点只与 $G_1,G_2$ 相连，因此只需判 $C(G_1,G_2)$ 是否在 $A,B$ 的简单路径上。

时间复杂度线性对数，瓶颈在于求 LCA。代码。

*V. P3225 [HNOI2012] 矿场搭建

不那么套路的连通性相关题目。

题目希望我们给出一种选择关键点的方式，满足删去任何一个点后形成的每个连通块内都存在至少一个关键点。

我们发现，由于删去非割点后整张图仍连通，所以删去非割点后连通块存在关键点蕴含于删去割点后连通块存在关键点。

唯一的特例是整张图点双连通。此时从图上任意选择两点作为关键点均合法，方案数为 ${\displaystyle (\genfrac{}{}{0ex}{}{|V|}{2})}$。选择两个是因为防止其中一个关键点被删去。

进行特判后，每个点双至少有一个原图上的割点。

为了解题，我们需要深入剖析广义圆方树的结构。剔除广义圆方树上所有叶子，即原图的非割点，我们得到了广义圆方树的由原图割点和点双方点构成的骨架，称为主干树。

定义一个点双的度数等于它对应的方点在主干树上的度数，等价于该点双包含的原图割点数量。

考虑一个大小为 $s$ 的点双。若其度数为 $1$，那么它是主干树的叶子，其内部需要有一个关键点，方案数 $s-1$。否则它有两个或以上的割点，我们发现若其包含的任意一个割点被删去，我们总可以走其它割点到达某个主干树的叶子，因此其内部不需要割点。

进一步地，我们发现删去主干树上任何一个割点，形成每个连通块必然包含至少一个主干树的叶子。因此方案合法。

综上，令主干树的叶子对应点双大小分别为 $s_1,s_2,\cdots ,s_k$，则第一问的答案为 $k$，第二问的答案为 $\prod _{i=1}^k(s_i-1)$。

时间复杂度线性。代码。

VI. CF487E Tourists

一道圆方树经典题。

$c$ 在 $a\to b$ 的简单路径上当且仅当 $c$ 与 $a\to b$ 某个方点相邻。因此，令方点的权值为对应点双所有节点权值最小值，将圆方树树剖即可回答询问。

问题在于修改点权时可能影响到很多方点权值，无法承受。考虑使用 只维护儿子信息 的技巧，将方点权值改为所有儿子的权值最小值，用 multiset 维护。修改圆点权值时修改其父节点的 multiset 并更新其父节点权值。

查询同样求出 $a\to b$ 点权最小值。当 LCA 为方点时，答案还要与其父节点（若存在）取最小值。

时间复杂度 $\mathcal{O}((n+q\log n)\log n)$，代码。

*VII. P8456 「SWTR-8」地地铁铁

题解。

[P8331 ZJOI2022] 简单题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

CF1763F Edge Queries

这题是不是有点裸？题目给的性质乱七八糟，完全没用。

建出圆方树，则 $a,b$ 之间涉及到的所有点双即 $a,b$ 在圆方树简单路径上的所有方点。

对于 $a,b$ 路径上的一个点双，如果其不为两点一边即割边，则删去其中任意一条边 $a,b$ 仍相互可达。因此，对于所有点双，若其为两点一边，则给其对应方点赋值 $0$，否则赋点双内部边的条数作为权值，则询问 $a,b$ 的答案即 $a,b$ 在圆方树上的简单路径上的所有方点的权值之和。

视 $n,m,q$ 同级，时间复杂度 $\mathcal{O}(n\log n)$。代码。

4. 支配树

由于 NOI 不可能考一般有向图的支配树（考了也写不动啊），所以这玩意以后再学。

4.1 定义

对有向图 $G=(V,E)$，选定一个起点 $s$（若有多个，可以新建虚点向所有起点连边转化为单个起点）。若从 $s$ 到 $y$ 的所有路径均经过 $x$，即 $x$ 是 $y$ 从 $s$ 出发的必经点，我们称 $x$ 支配 $y$。

容易证明支配关系具有

• 传递性：若 $x$ 支配 $y$，$y$ 支配 $z$，则 $x$ 支配 $z$。
• 自反性：$x$ 支配 $x$。
• 反对称性：若 $x$ 支配 $y$，$y$ 支配 $x$，则 $x=y$。

这保证了支配是偏序关系，但偏序关系只能建出 DAG，不够优秀。

支配关系有一条特殊性质：若 $x,y$ 均支配 $z$，则 $x,y$ 之间也有支配关系。反证法，考虑 $s\to z$ 的任意一条路径，据条件 $x,y$ 必然在路径上。若 $x$ 在 $y$ 之前，因为 $x$ 不支配 $y$，所以 $1\to y\to z$ 可以不经过 $x$，与 $x$ 支配 $z$ 矛盾；对于 $y$ 在 $x$ 之前的情况同理。

不妨称这种性质为半完全性。其重要之处在于，任何具有半完全性的系统均可以建树：考虑支配 $y$ 的所有点 $D_y=\{x_1,x_2,\cdots ,x_k\}$，对其中任意两个元素 $x_i,x_j(i\ne j)$ 应用半完全性，可知 $D_y$ 内的所有元素形成了 全序 关系：任意两个元素均可比较，则所有 $x_i$ 的关系可以用一条链描述。

因此，令 $ido{m}_i$ 表示 $D_i=\{x_1,x_2,\cdots ,x_k\}$ 当中被其它所有点支配的 $x_j$。$ido{m}_i$ 称为 $i$ 的直接支配点（immediate dominator），可以理解为 $i$ 的所有支配点当中除 $i$ 本身以外距离 $i$ 最近的那一个。特殊地，$ido{m}_s$ 不存在（类似树根不存在父节点）。

在 $i$ 和 $ido{m}_i$ 之间连边，我们就得到了支配树。根据半完全性，一个节点在支配树上的祖先集合就是支配它的所有节点。

支配树用于描述有向图在给定起点时节点的必经性，类似广义圆方树完整地描述了无向图的必经性。

4.2 DAG 支配树

有向无环图具有特殊性质，使得我们能够方便地求出其支配树。

对 DAG 拓扑排序，设当前节点为 $x$。根据拓扑排序的性质，$x$ 对拓扑序在它之前的节点的必经性没有影响，因为 $x$ 甚至不可达它们。因此，考虑到 $x$ 时，我们只需求出 $ido{m}_x$，不需要更改其它节点的 $idom$。

当 $x$ 只有一条入边 $y\to x$ 时，$ido{m}_x$ 很显然是 $y$。到达 $x$ 必然要走 $y\to x$ 这条边，所以 $y$ 支配 $x$，推出 $y$ 及其在支配树上的所有祖先 $anc(y)$ 都是 $x$ 的支配点（支配的传递性），而 $y$ 则是距离 $x$ 最近的那一个。

当 $x$ 有两条入边 $y\to x$ 和 $z\to x$ 时，若到达 $x$ 走 $y\to x$ 这条边，则集合 $anc(y)$ 是必经点；同理，若走 $z\to x$ 这条边，则集合 $anc(z)$ 是必经点。据定义，$x$ 的支配点是 $anc(y)$ 与 $anc(z)$ 的交集（不在交集内的某个节点均可以通过走 $y\to x$ 或 $z\to x$ 绕过去）加上 $x$，前者即 $anc(lca(y,z))$。因此，$ido{m}_x=lca(y,z)$。

通过上述推理，我们容易发现，若 $x$ 有入边 $y_i\to x$，则 $anc(x)\mathrm{\setminus }x$ 等于 $\bigcap _{i=1}^{k}anc(y_i)$，所以

$$ido{m}_x=lca(y_1,y_2,\cdots ,y_k)$$

因为拓扑序在 $x$ 之前的节点均已经确定了其 $idom$，所以在确定每个节点的 $idom$ 后预处理倍增数组，倍增求 LCA 即可做到 $\mathcal{O}((n+m)\log n)$。代码见例 I.

4.3 例题

I. P2597 [ZJOI2012] 灾难

一道经典的 DAG 支配树问题，代码。

5. DAG 链剖分

前置知识：树链剖分。

DAG 链剖分在国内信息学算法竞赛界第一次被系统阐述是在 2022 年戴江齐学长的集训队论文中。它看上去是比较新的科技，但实际上很早就有 DAG 链剖分相关的题目了（GRE Words Once More）。

5.1 算法介绍

DAG 链剖分的核心思想和树链剖分类似，都是通过 设置重儿子 的方法将图剖分成若干条链，使得图上任意路径经过的链的条数在可接受的范围内。

若原图存在若干无入度的节点，则新建源点向它们连边。因此，可以规范 DAG 的形态仅有节点 $1$ 无入度。设 $f_i$ 表示从 $i$ 出发的路径条数。

从树剖出发，考虑定义重儿子为 $f$ 值最大的后继。形式化地，$so{n}_i={\mathrm{argmax}}_{j\in suc(i)}{f}_j$，并称 $i\to so{n}_i$ 为重边。将所有重边建图得到内向森林。容易发现对于任意轻边 $i\to j$，$2f_j\le f_i$，因为 $f_i=1+\sum _{j\in suc(i)}{f}_j$ 且存在 $j^{\prime }\in suc(i)$ 使得 $f_{j^{\prime }}\ge f_j$。这种结构配合倍增可以解决部分题目，但不够优秀，我们希望 $i\to so{n}_i$ 形成链而不是树。为此，每个节点的入度也不应大于 $1$。

因此，设 $g_i$ 表示从 $1$ 到 $i$ 的路径条数。显然 $g_j=[j=1]+\sum _{j\in suc(i)}{g}_i$。设 $i\to j$ 为重边当且仅当 $j$ 为 $i$ 的 $f$ 值最大的后继，且 $i$ 为 $j$ 的 $g$ 值最大的前驱。这样每个点的出度和入度均不大于 $1$。容易发现对于任意轻边 $i\to j$，要么 $2f_j\le f_i$，要么 $2g_i\le g_j$，因此每走一条轻边，要么 $f$ 值减半，要么 $g$ 值翻倍。因此一条路径上的轻边条数为 $\mathcal{O}(\log V)$ 级别，其中 $V$ 为路径条数。这说明 只有当路径条数不大时 DAG 链剖分才适用。

DAG 链剖分常与后缀自动机结合，因为字符串 $|s|$ 的后缀自动机的 DAWG 的路径条数为 $s$ 的本质不同子串数，且剖分 DAWG 后可以快速定位字符串查询相关信息。更重要的是可以用 $\log$ 条时间戳连续的链描述从 $s[l,r_1]$ 到 $s[l,r_2]$ 的路径，我们将在例题中看到这非常有用。

5.2 例题

*I. UOJ752 Border 的第五种求法

感觉思想挺简单的，但是是未曾设想的道路。

对 $s$ 建出 SAM，则 $B$ 是 $s[l,r]$ 的 border 当且仅当：

• $B$ 是 $s[l,r]$ 的前缀。
• $B$ 在 link 树上是 $s[1,r]$ 的祖先。

因为 $s[l,r]$ 的所有前缀形成 DAWG 上一条路径，考虑 DAG 剖分将路径拆成 $\log n$ 条时间戳连续的重链，则问题转化成 $\mathcal{O}(q\log n)$ 次询问 $s[1,r]$ 到根的路径上时间戳落在某区间的节点的权值和，而 $i$ 的权值即 $f_{|\mathrm{endpos}(i)|}$。

• 如何拆重链：容易求出当前节点 $i$ 到重链末尾形成的字符串在原串上的任意对应下标 $[l,r]$。不妨设当前要匹配 $s[x,y]$，则当前重链匹配长度即 $|lcp(s[l,r],s[x,y])|$，容易 SA 或者 SAM 求出。

二维数点，离线后在树上扫一遍，用 BIT 维护单点修改区间查询。时间复杂度 $\mathcal{O}(n\log n+q{\log }^{2}n)$，代码。

*II. CF1098F Ж-function

提供一个比较好想的思路。

一句话题解：DAG 链剖分 + P4211 + 处理算错的贡献。

翻转 $s$ 将问题转化为求 $s[l,r]$ 的每个前缀与 $s[l,r]$ 的最长公共后缀。众所周知两串 LCS 可以用 SAM 的 link 树的 LCA 的 $len$ 值大致描述，仅有当两串存在祖先后代关系时需要特殊考虑。因此，不妨先求

$$\sum _{p=l}^{r}len(lca(s[l,p],s[l,r]))$$

考虑上式，发现形式很像经典老题 P4211 [LNOI2014] LCA。问题在于 $s[l,p]$ 随着 $p$ 从 $l$ 增大到 $r$，其取值和 $l$ 有关，我们不能对每个 $l$ 都做一遍离线扫描线。注意到它是 DAWG 的路径，因此考虑 DAG 链剖分。将其剖成 $\mathcal{O}(\log n)$ 条 DAWG 上时间戳连续的链，这样只需按 DAWG 时间戳的顺序扫描线。也就是说，我们将问题转化为了 $\mathcal{O}(n)$ 次加入，$\mathcal{O}(q\log n)$ 次查询的 P4211。将 link 树树剖，用 BIT 维护区间给 $c_i$ 加 $1$，区间查询 $c_i{v}_i$ 之和，其中 $v_i$ 即时间戳为 $i$ 的节点 $u$ 的 $len$ 值减去其父亲的 $len$ 值，这样 $x$ 处的修改对 $y$ 处的查询的贡献即 $len(lca(x,y))$。这部分时间复杂度 $\mathcal{O}(q{\log }^{3}n)$，但三个 $\log$ 分别是 DAG 链剖分，树剖，BIT，而难以构造使得 link 树卡满前两个 $\log$ 的字符串 $s$，所以常数非常小。

然后我们处理算错的贡献。因为 $s[l,p]$ 不可能是 $s[l,r]$ 的后代，所以只需考虑 $s[l,p]$ 是 $s[l,r]$ 的祖先的情况。此时减去 $len(s[l,p])$，加上 $p-l+1$。每一条 DAWG 上时间戳连续的链 $[ql,qr]$ 相当于查询 $s[l,r]$ 到根的路径上，在 DAWG 上时间戳 $t$ 落在 $[ql,qr]$ 范围内的节点 $x$ 对应的 $s[l,p]$ 的 $p-l+1-len(x)$ 之和。$-len(x)$ 容易树上线段树前缀和预处理，但 $p-l+1$ 该怎么办？每个节点可能对应多个长度 $[len(fa(x))+1,len(x)]$，不能和 $-len(x)$ 放在一起预处理。但注意到，我们容易求出 $[ql,qr]$ 对应的 $p$ 的范围 $[pl,pr]$，而时间戳随着 $p$ 增大同样连续，因此时间戳 $t$ 对应的 $p-l+1$ 又可以写为 $pl+(t-ql)$。该式 $pl,ql$ 都是定值，只有 $t$ 和每个节点有关，而显然每个节点只有一个时间戳，因此线段树额外维护落在当前范围内的时间戳之和以及个数即可。这部分时间复杂度 $\mathcal{O}((n+q){\log }^{2}n)$。

注意第一部分因为离线，空间复杂度必须 $q\log n$。为减小空间开销，第二部分需要离线 dfs 解除祖先限制做到空间复杂度线性。总时间复杂度 $\mathcal{O}((n+q\log n){\log }^{2}n)$，擦时限通过。代码。

6.1 Dilworth 定理

CF1738G Anti-Increasing Addicts

果然还是 Anton 出的题最智慧。

初步感知问题：

• 当没有限制一些位置必须保留时，直接删去 $(n-k+1)\times (n-k+1)$ 的正方形即可满足条件。

• 题目要求不能出现保留位置不出现长度为 $k$ 的链，根据 dilworth 定理，必须用不超过 $k-1$ 个反链覆盖所有保留位置。

• $k-1$ 条反链至多覆盖 $n^2-(n-k+1{)}^2$ 个位置，因为第一条反链至多覆盖 $2n-1$ 个位置，第二条反链至多覆盖 $2n-3$ 个位置。想象每次剥去正方形的一行一列。因此，反链覆盖位置是极大的，限制已经最严格。

设 $f_{x,y}$ 表示从 $(x,y)$ 开始的只经过保留位置的最长链长度。显然若存在 $f_{x,y}=k$ 则无解，因为我们被强制保留长度为 $k$ 的链。否则我们尝试用 $k-1$ 条反链在最大化覆盖位置的同时，覆盖到所有强制保留的位置。

根据 $f_{x,y}$ 的值将位置分层，值相同的位置必然形成一条反链，否则 $p\to q$ 形成链，$f_p$ 可以更大。

为了让最大化覆盖位置，不妨设第 $i$ 条反链从 $(n,i)$ 开始，每次向上或向右走，经过所有未被覆盖的 $f$ 值为 $k-i$ 的位置并将经过的点全部覆盖，最终走到 $(i,n)$。若反链互不相交，则覆盖位置之和为 $\sum _{i=1}^{k-1}2(n-i)+1$，达到最大值。

为此，我们规定反链 能向上走就向上走。也就是说，当且仅当上方已经被覆盖或再往上走就无法覆盖某个 $f$ 值为 $k-i$ 的位置时，我们才会向右走。为此，设 $li{m}_{v,y}$ 表示第 $y$ 列及其右侧 $f$ 值为 $v$ 的位置的行数最大值，若当前 $x=f_{k-i,y+1}$ 则无法继续往上走，否则无法覆盖 $y+1$ 及其右侧 $f$ 值为 $v$ 的行数最大的位置。

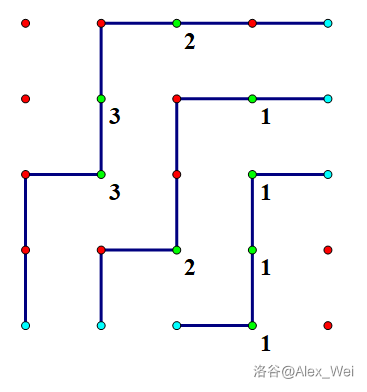
如上图。

只需证明第 $i$ 条反链必然经过 $(n-k+i,i)$ 和 $(i,n-k+i)$ 即可证明合法方案一定存在，而这是容易的。对于第 $i$ 条反链，在第 $i+1$ 列及其右侧不会出现行数大于 $n-k+i$ 的 $f$ 值为 $k-i$ 的位置 $(x,y)$，其中 $x>n-k+i$，因为否则其对应链末端的行数 $x^{\prime }\ge x+(k-i)>n$，不合法。因此，根据 尽量向上走 原则，从 $(n,i)$ 出发一定可以走到 $(n-k+i)$。同理可证最终必然经过 $(i,n-k+i)$。

$f$ 可以直接二维前缀最大值求出，时间复杂度 $\mathcal{O}(n^2)$。实际上将 $f$ 直接当成二维前缀最大值数组也是对的，因为它不影响任何东西，证明略。代码。

参考资料

第二章：

• 算法学习笔记（71）：2-SAT - Pecco。
• 【计算理论】计算复杂性（NP 完全问题 - 布尔可满足性问题 | 布尔可满足性问题是 NP 完全问题证明思路）- 韩曙亮。
• 合取 - 百度百科。
• 2-SAT 适定性 (Satisfiability) 问题知识点详解 - zeng_jun_yv。

第三章：

• 【算法学习】圆方树 - 粉兔。

第四章：

• 支配树 瞎学笔记 - ycx060617。
• 【学习笔记】支配树_cz_xuyixuan。

第五章：

• 国家候选队互测 2022 Round #1 题解。