多项式 I:拉格朗日插值与快速傅里叶变换
1. 复数和单位根
前置知识:弧度制,三角函数。
1.1 复数的引入
跳出实数域
像这种从
将
- 加法:
- 减法:
- 乘法:
- 除法:
1.2 复平面与棣莫弗定理
描述一个复数
一个复数唯一对应一个平面向量,因为它们都可以用有序实数对描述。将向量起点平移至原点,则其终点指向与其对应的复数。考虑平面向量的一些特征,如其长度与所在直线斜率。将这些概念应用在复数上,我们得到如下定义:
- 定义复数
- 定义复数
- 辐角确定了
根据
利用
- 根据棣莫弗定理,我们得到对虚数单位
1.3 单位根的定义
当
考虑将单位圆
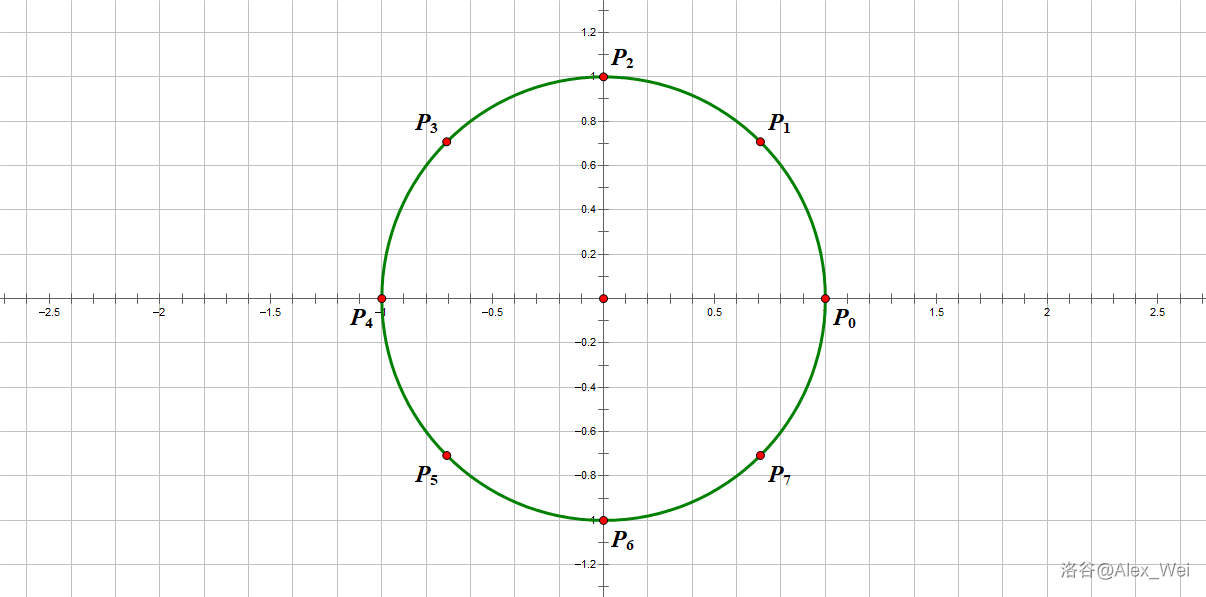
探究
根据
可以观看 3b1b 的视频 从 6:00 到 7:30 的部分加深对上述内容的理解。
- 单位根的循环性:由
- 当
- 单位根的对称性:因为
- 若
1.4 单位根与原根
前置知识:原根,详见 初等数论学习笔记 I:同余相关。
单位根和原根有极大的相似性,可以说原根就是模
设
- 单位根和原根都是对应域上一个大小为
快速傅里叶变换 FFT 和快速数论变换 NTT 的联系恰在于此。
1.5 欧拉公式
前置知识:自然对数
这部分为接下来可能用到的符号做一些补充。
欧拉公式指出
即单位圆上从
欧拉公式的严谨证明超出了讨论范围,相关资料可以参考百度百科。我们给出一个对欧拉公式的感性理解方式,以加深读者对欧拉公式的直观印象与理解,来自 在 3.14 分钟内理解
根据
根据
当
这样,
将该表示法应用至单位根,可知
读者应当在
带入
带入
这说明对于任意
2. 多项式
2.1 基本概念
形如
当项数无限时,和式形如
- 多项式 系数非零 的最高次项的次数称为该多项式的 度,也称次数,记作
- 使得
- 若
- 代数基本定理:任何非零一元
2.2 系数表示法和点值表示法
将
考虑这两种表示法之间的联系。我们尝试探究在给定
一个自然的猜测是
证明即考虑直接带入,得到
因
综上,我们得到重要结论:
- 从系数表示法转为点值表示法称为 求值(Evaluation)。
- 从点值表示法转为系数表示法称为 插值(Interpolation)。
2.3 多项式运算
2.3.1 基本运算
设
- 设
- 设
因此,在系数表示法下,计算两个多项式相加的复杂度为
-
根据
-
根据
因此,在点值表示法下,计算两个多项式相加需要
- 用
在系数表示法下计算两个多项式相乘,我们首先将其转化为点值表示法,相乘后再转回系数表示法。时间复杂度
3. 拉格朗日插值
在 2.2 小节我们得到结论:
从系数表示法转为点值表示法,最常用的方法是直接带入,时间复杂度
从点值表示法转为系数表示法,最直接的方法是高斯消元,时间复杂度
3.1 算法详解
拉格朗日插值的核心思想在于利用点值的可加性,每次只考虑一个点值,其它点值均视为
为了让
对
为得到
通常情况下,题目要求我们求出
多项式快速插值在
3.2 连续取值插值
当给定点值横坐标为连续整数时,我们有快速单点插值的方法。
以
分子是
分母对于
因此
预处理阶乘逆元,时间复杂度
3.3 应用
- 计算范德蒙德方阵的逆矩阵,详见 4.4.1 小节。
3.4 例题
P4781 【模板】拉格朗日插值
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e3 + 5;
constexpr int mod = 998244353;
int ksm(int a, int b) {
int s = 1;
while(b) {
if(b & 1) s = 1ll * s * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return s;
}
int n, k, ans, x[N], y[N];
int main() {
cin >> n >> k;
for(int i = 1; i <= n; i++) cin >> x[i] >> y[i];
for(int i = 1; i <= n; i++) {
int deno = 1, nume = 1;
for(int j = 1; j <= n; j++) {
if(i == j) continue;
deno = 1ll * deno * (x[i] + mod - x[j]) % mod;
nume = 1ll * nume * (k + mod - x[j]) % mod;
}
ans = (ans + 1ll * y[i] * nume % mod * ksm(deno, mod - 2)) % mod;
}
cout << ans << "\n";
return 0;
}
4. 快速傅里叶变换
快速傅里叶变换(Fast Fourier Transform,FFT)是多项式算法的根基。想要真正理解它,必须先真正理解单位根,还需要对线性代数有基本了解。
推荐观看:
- 这个算法改变了世界 - Veritasium。
- The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever? - Reducible & B 站搬运。
4.1 求值的本质
设
这样,如果有
左侧矩阵就是著名的 范德蒙德矩阵。
当
朴素计算求值的复杂度为
4.2 离散傅里叶变换
在介绍 FFT 之前,我们先给出离散傅里叶变换(Discrete Fourier Transform,DFT)的概念。
DFT 在工程中是将离散信号从时域转为频域的过程。碰巧的是,其表达式刚好可以用来对多项式进行多点求值,只不过这些点值是固定的 单位根 处的点值,但对于求值做多项式乘法已经足够了。
DFT 将一个长度为
也即
设多项式
根据上式,离散傅里叶变换可以看成多项式
没看懂?没关系。接下来我们将从另一角度出发,得到一个差别微小但更容易理解的算法 —— FFT。
4.3 算法详解
首先我们得搞清楚,DFT 是一个变换,而 FFT 是用于实现 DFT 的算法。在 FFT 的推导过程中,其所实现的变换和 DFT 变换有细微的差别,因此笔者也用 FFT 表示该算法实现的变换。
按理说学习一个算法时需要搞清楚它的用途,但如果直接从 DFT 角度入手尝试简化流程,那么为了让动机看起来自然,我们还要先学习 DFT 的实际含义,这涉及到大量前置知识。
但是,从计算机科学界尤为重要且为各位 OIer 熟知的多项式乘法的优化出发,我们通过自然推理得到一个算法,而该算法恰好可以快速实现 DFT(有一些细小的差别,详见 4.3.5)。
我们明确接下来的目标:给定次数
下文中,
4.3.1 简化情况
解决一个普遍性的问题,最重要的思想就是 从简化情况入手,分析问题的性质。
函数的性质无非就那几个:奇偶性,单调性,周期性等。一般函数没有单调性和周期性,但总可以表示为一个偶函数和一个奇函数之和,这一定是突破点。
-
对于偶函数
-
对于奇函数
因此,将任意多项式
选择
不妨设
但是
因为
同理,从
因此,
这样才是真正意义上的规模减半。若问题可递归,则时间复杂度为
4.3.2 引入单位根
问题来了,如何保证递归得到的问题也满足两两互为相反数呢?
考虑一开始的
进一步推演,因为问题会递归
逆推得到结果后,我们再顺着检查一遍:初始令
由此可得通常使用(补齐到
4.3.3 递归公式
得到大致框架后,我们具体地描述整个算法流程:
首先将
设当前需要求值的多项式
将
根据单位根的性质(在单位根部分有介绍):
得
这样,我们只需求出
4.3.4 蝴蝶变换
递归处理比较慢,我们希望像位运算卷积一样通过递推实现整个过程。
因为在边界条件下,每个位置的取值与其对应的系数相关,所以递归转递推的关键在于考察系数的变化。
考虑
进行第一层递归时,将
进行第二层递归时,类似地将每个子问题的
进行第三层递归时,共有
我们看到,如果一个系数在规模为
进一步地,一个系数在第
这就说明,
因此我们断言,系数
因此,在算法一开始先对系数数组
进一步地,根据
这就是 FFT,整个过程称为 对多项式
4.3.5 DFT 和 FFT
对比 DFT 和 FFT 矩阵:
可以发现 DFT 和 FFT 基本一致,它们的差别在于:
- 朴素 FFT 要求
- DFT 和 FFT 带入单位根的顺序是相反的。
注意这些细微差别,不要把 DFT 和 FFT 搞混了。
4.3.6 循环卷积
4.4 离散傅里叶逆变换
离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)可以视为单位根处插值的过程。即给出
类似地,IDFT 和 IFFT 之间也存在一些差异。想必各位读者根据之前的内容已经可以猜出这种差异是什么了。
4.4.1 范德蒙德方阵逆
考虑范德蒙德方阵
这玩意怎么求逆?我们考虑最暴力的方法:拉格朗日插值!
因为范德蒙德方阵可以看成多项式多点求值,根据
再结合拉格朗日插值公式
可知从
这就是范德蒙德方阵逆当中每个元素的表达式。
4.4.2 算法介绍
很显然,
因此,只需对快速傅里叶变换的矩阵求逆,即可得到快速傅里叶逆变换的矩阵。
设
则
分子和分母均形如
首先,因为
模拟短除法
因此
这就说明
因此,对一个序列做 IFFT,只需将 FFT 递归公式里面的
这就引出了 IDFT 公式及其对应矩阵:
4.5 快速多项式乘法
通过 FFT 和 IFFT,我们可以在
计算两个次数分别为
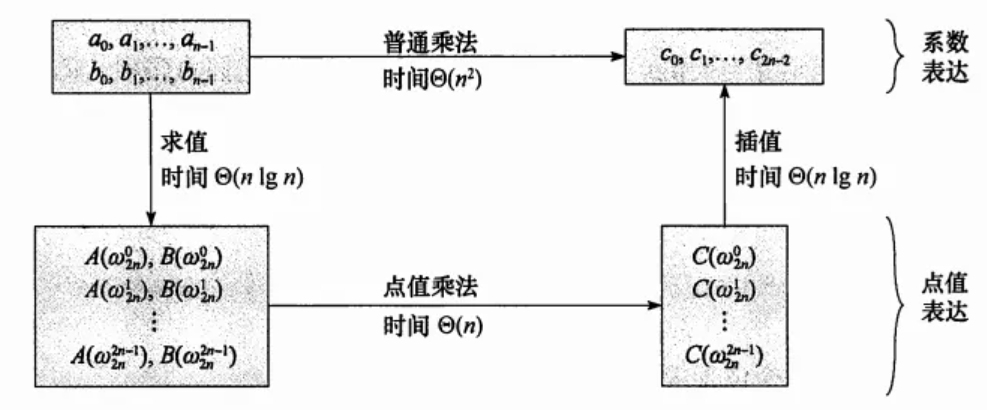
首先我们需要实现一个复数类,它支持复数的加减乘运算。也可以使用 C++ 自带复数类 std::complex<T>,用法见 CPP reference。
FFT 和 IFFT 大体上一致,只有一些细小差别。我们可以类似实现 FWT 和 IFWT 那样,用同一个函数实现它们,并用一个参数区别。
等式
- 注意浮点数的精度。当多项式系数的绝对值较大时,需使用
long double甚至 5.2 小节的任意模数卷积。
模板题 P3803 代码:
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1 << 21;
constexpr double pi = acos(-1);
struct comp {
double a, b; // a + bi
comp operator + (const comp &x) const {return {a + x.a, b + x.b};}
comp operator - (const comp &x) const {return {a - x.a, b - x.b};}
comp operator * (const comp &x) const {return {a * x.a - b * x.b, a * x.b + b * x.a};}
} f[N], g[N], h[N];
int n, m, r[N];
void FFT(int L, comp *f, bool type) { // L 表示长度, type = 1 表示 FFT, type = 0 表示 IFFT
for(int i = 1; i < L; i++) {
r[i] = (r[i >> 1] >> 1) + (i & 1 ? L >> 1 : 0);
if(i < r[i]) swap(f[i], f[r[i]]);
}
for(int d = 1; d < L; d <<= 1) {
comp wd = {cos(pi / d), sin(pi / d)}; // 2d 次单位根
if(!type) wd.b = -wd.b; // IFFT 单位根取倒数, 相当于沿 x 轴对称
static comp w[N];
w[0] = {1, 0};
for(int j = 1; j < d; j++) w[j] = w[j - 1] * wd; // 用数组记录 0 ~ d-1 次单位根, 减少复数乘法次数
for(int i = 0; i < L; i += d << 1) {
for(int j = 0; j < d; j++) {
comp x = f[i | j], y = w[j] * f[i | j | d];
f[i | j] = x + y, f[i | j | d] = x - y;
}
}
}
if(!type) for(int i = 0; i < L; i++) f[i].a /= L; // IFFT 时所有数要除以长度 L, 我们只用到了实部所以只需将实部除以 L
}
int main() {
cin >> n >> m;
for(int i = 0; i <= n; i++) cin >> f[i].a;
for(int i = 0; i <= m; i++) cin >> g[i].a;
int L = 1;
while(L <= n + m) L <<= 1;
FFT(L, f, 1), FFT(L, g, 1);
for(int i = 0; i < L; i++) h[i] = f[i] * g[i];
FFT(L, h, 0);
for(int i = 0; i <= n + m; i++) cout << (int) (h[i].a + 0.5) << (i < n + m ? ' ' : '\n');
return 0;
}
4.6 快速数论变换
前置知识:原根和阶。
我们将 DFT 的数值范围从复数域推广至任意存在
也可以视作
类似可知 IDFT
即 DFT 和 IDFT 对序列进行的变换的本质抽象。
4.6.1 算法介绍
快速数论变换即在模
设变换长度为
第一条性质保证
根据原根的性质,
因此,
常见 NTT 模数有:
如果不是常见模数,我们需要检验
注意以上只是模数
4.6.2 代码实现
朴素 NTT 已经比 FFT 快了不少,因为复数运算很耗时。
接下来加入一些常数优化:
- 预处理
- 用
unsigned long long和
综上,写出如下代码(依然是 模板题):尽管题目没有要求取模,但可视为在模
#include <bits/stdc++.h>
using namespace std;
using ull = unsigned long long;
constexpr int N = 1 << 21;
constexpr int mod = 998244353;
constexpr int ivg = (mod + 1) / 3;
int ksm(int a, int b) {
int s = 1;
while(b) {
if(b & 1) s = 1ll * s * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return s;
}
int n, m, r[N], f[N], g[N], h[N];
void FFT(int L, int *a, bool type) {
static ull f[N], w[N];
for(int i = 0; i < L; i++) f[i] = a[r[i] = (r[i >> 1] >> 1) | (i & 1 ? L >> 1 : 0)];
for(int d = 1; d < L; d <<= 1) {
int wd = ksm(type ? 3 : ivg, (mod - 1) / (d + d));
for(int j = w[0] = 1; j < d; j++) w[j] = 1ll * w[j - 1] * wd % mod;
for(int i = 0; i < L; i += d << 1) {
for(int j = 0; j < d; j++) {
int y = w[j] * f[i | j | d] % mod;
f[i | j | d] = f[i | j] + mod - y, f[i | j] += y;
}
}
if(d == (1 << 16)) for(int p = 0; p < L; p++) f[p] %= mod;
}
int inv = ksm(L, mod - 2);
for(int i = 0; i < L; i++) a[i] = f[i] % mod * (type ? 1 : inv) % mod;
}
int main() {
cin >> n >> m;
for(int i = 0; i <= n; i++) cin >> f[i];
for(int i = 0; i <= m; i++) cin >> g[i];
int L = 1;
while(L <= n + m) L <<= 1;
FFT(L, f, 1), FFT(L, g, 1);
for(int i = 0; i < L; i++) h[i] = 1ll * f[i] * g[i] % mod;
FFT(L, h, 0);
for(int i = 0; i <= n + m; i++) cout << h[i] << (i < n + m ? ' ' : '\n');
return 0;
}
5. 应用与技巧
FFT 和 NTT 是所有快速多项式操作的基础。
设多项式
5.1 常数优化
在分析变换次数的时候,一般不区分 DFT 和 IDFT。
5.1.1 三次变两次优化
计算两 实系数 多项式
根据
这样,三次 DFT 变成了两次 DFT,对常数有显著优化。代码。
这个优化被接下来稍复杂的技巧完全包含,它们的核心思想都是利用实系数的性质。
5.1.2 合并两次实系数 DFT
同时计算两 实系数 多项式
类似地,我们设
在给出做法之前,我们还要引入一些复数相关的概念:
- 定义:对于两个复数
- 表示:复数
- 运算性质:两个共轭复数的辐角互为相反数,即
- 易知复数和的共轭等于它们共轭的和,且一个复数的共轭的共轭等于它本身。
首先,
求得
5.1.3 合并两次实系数 IDFT
这里实系数指 IDFT 后的各项系数为实数。如果是 IDFT 前的各项系数为实数,直接使用上一小节的技巧即可。
设需要 IDFT 的两个多项式为
5.2 任意模数卷积
给定两多项式
若 long double 也无法接受。
接下来介绍两种常见的解决该问题的方法。它们也被称为 MTT(非正式),得名于毛啸 2016 年的集训队论文。
5.2.1 拆系数 FFT
设
显然有一个四次 DFT 和三次 IDFT 的朴素做法:对
使用 6.1.2 和 6.1.3 的技巧,可以做到两次 DFT 和两次 IDFT。系数值域
模板题 P4245 任意模数多项式乘法 的 代码。注意用 long double,double 会被卡精度,或者换一种精度较高的 FFT 写法。
5.2.2 三模数 NTT
前置知识:(扩展)中国剩余定理。
选取三个常用 NTT 模数,分别算出
我们选择
如果使用 CRT,则需要 __int128,因为
使用 exCET 就不需要 __int128:
- 合并
- 合并
效率比拆系数 FFT 低不少,因为进行了九次 DFT。代码。
5.3 分治 NTT
前置知识:CDQ 分治。
分治 NTT 在信息竞赛界应用广泛,这归功于他所解决的问题:形如
5.3.1 算法介绍
形如给定
我们不能通过简单的 NTT 解决这个问题,因为
这是一个在线的问题,考虑使用 CDQ 分治 转化为静态问题。
- 设当前分治区间为
- 若
- 否则,令
- 为了求解
- 向右递归
因为
模板题 P4721 分治 FFT 代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
constexpr int N = 1 << 17;
constexpr int mod = 998244353;
void add(int &x, int y) {x += y, x >= mod && (x -= mod);}
int ksm(int a, int b) {
int s = 1;
while(b) {
if(b & 1) s = 1ll * s * a % mod;
a = 1ll * a * a % mod, b >>= 1;
}
return s;
}
int n, f[N], g[N];
void solve(int l, int r) {
if(l == r) return;
int m = l + r >> 1, L = 1;
solve(l, m);
while(L < r - l + 1) L <<= 1;
static int a[N], b[N], c[N];
memset(a, 0, L << 2);
memcpy(a, f + l, m - l + 1 << 2);
memcpy(b, g, L << 2);
NTT(L, a, 1), NTT(L, b, 1);
for(int i = 0; i < L; i++) c[i] = 1ll * a[i] * b[i] % mod;
NTT(L, c, 0);
for(int i = m + 1; i <= r; i++) add(f[i], c[i - l]);
solve(m + 1, r);
}
int main() {
cin >> n;
for(int i = 1; i < n; i++) scanf("%d", &g[i]);
f[0] = 1, solve(0, n - 1);
for(int i = 0; i < n; i++) printf("%d%c", f[i], i + 1 < n ? ' ' : '\n');
return 0;
}
5.3.2 阶梯网格路径计数
阶梯网格路径计数是一类可以使用分治 NTT 解决的经典问题。
给定
当然,问题没有这么简单。我们限制第
显然有
考虑一段
在不受
稍作思考,设
进一步地,为了避免在
综合上述分析,我们将问题转化为:从
因此,从
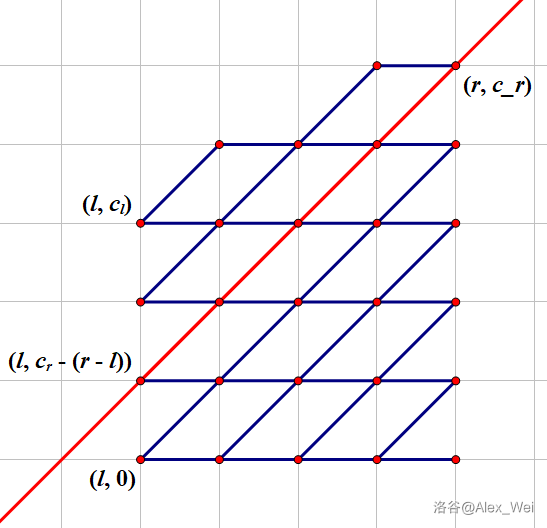
有了大致思路,设计算法就很简单了:设
对于
对于
两部分相加即得
边界
两次下传
接下来对问题进行一些扩展:
- 如果没有
5.4 例题
CF1770G Koxia and Bracket
相比于 F,这道题就略显套路了。
将左括号视为
对于
设
非常明显的阶梯格路计数问题,稍有变形,不过解法大差不差,核心思想是一致的:考虑
对于本题,就是
每个分治区间涉及到的多项式长度不超过其父区间长度,因此时间复杂度为
参考资料
第一章:
- 复数 - OI Wiki。
- 复数 - 百度百科。
- [Video] 虚数的来源 - Veritasium。
- [Video] 【官方双语】微分方程概论 - 第五章:在 3.14 分钟内理解
第二章:
第四章:
- 快速傅里叶变换 - OI Wiki。
- FFT 理性瞎扯 - xtx1092515503。
- Vandermonde matrix - Wikipedia。
- Discrete Fourier transform - Wikipedia。
- 浅谈范德蒙德 (Vandermonde) 方阵的逆矩阵的求法以及快速傅里叶变换 (FFT) 中 IDFT 的原理 - Deadecho。
- 范德蒙德矩阵的逆矩阵怎么计算? - FFjet 的回答 - 知乎。
- Discrete Fourier transform over a ring - Wikipedia。
- NTT 与多项式全家桶 - command_block。
- [Video] 这个算法改变了世界 - Veritasium。
- [Video] The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever? - Reducible & B 站搬运。
第五章:
- P3803 题解 - NaCly_Fish。
- 2016 集训队论文《再探快速傅里叶变换》—— 毛啸。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!