初等数论学习笔记 II：分解质因数

CHANGE LOG

2022.7.13：重构文章，更新 PR 模板代码。
2023.1.23：对文章进行修补。

1. Miller-Rabin

Miller-Rabin 素性测试是一种具有随机性的素数判定方法。它有一定概率将合数判定为素数，但不会将素数判定为合数。

素数判定的基本思路为根据所有质数但很少合数具有的性质，检查被判定的数是否具有这些性质。若不具有，则该数是合数，否则该数大概率是质数。

1.1 费马素性检验

当 $p$ 是素数时，对于任意 $a ⊥ p$ 均有 $a^{p - 1} \equiv 1 (\mod p)$ 。相反，当 $a^{p - 1} \equiv 1 (\mod p)$ 时，是否有 $p$ 是素数？

可惜命题并不成立。有极小概率使得 $a ⊥ p$ ， $p$ 是合数且 $a^{p - 1} \equiv 1 (\mod p)$ ，如当 $a = 2$ ， $p = 341$ 时， $2^{340} \equiv 1 (\mod 341)$ ，称 $341$ 是以 $2$ 为底的伪素数。 $341$ 是最小的伪素数基数。

若 $a^{p - 1} ≢ 1 (\mod p)$ ，则 $p$ 必然不是质数。多选几个与 $p$ 互质的数检查，可以排除大部分合数。这被称为费马素性检验，它具有随机性。

当面对形如 $561$ 的卡迈克尔数时，费马素性检验就相当劣了。卡迈克尔数 $p$ 满足所有与 $p$ 互质的数的 $p - 1$ 次方模 $p$ 均为 $1$ 。

1.2 二次探测定理

根据二次剩余部分的知识，当 $p$ 为奇素数时， $x^{2} \equiv 1 (\mod p)$ 有且仅有解 $\pm 1$ 。因此，若存在 $a \neq \pm 1$ 满足 $a^{2} \equiv 1 (\mod p)$ ，则 $p$ 必然不是质数。

这被称为 二次探测定理。

1.3 算法介绍

结合费马素性检验与二次探测定理。

根据二次探测定理，当 $a^{p - 1} \equiv 1 (\mod p)$ 时，若 $p - 1$ 是 $2$ 的倍数，则 $a^{\frac{p - 1}{2}}$ 必须是 $\pm 1$ 。若 $\frac{p - 1}{2}$ 仍是 $2$ 的倍数且 $a^{\frac{p - 1}{2}} \equiv 1 (\mod p)$ ，则 $a^{\frac{p - 1}{4}}$ 必须是 $\pm 1$ ，以此类推。

一般地，若 $p - 1$ 是 $2^{r}$ 的倍数且 $a^{\frac{p - 1}{2^{r - 1}}} \equiv 1 (\mod p)$ ，则 $a^{\frac{p - 1}{2^{r}}}$ 等于 $\pm 1$ ，否则 $p$ 不是素数。例如 $a = 2$ 且 $p = 341$ 。 $2^{340} \equiv 1 (\mod 341)$ ， $2^{170} \equiv 1 (\mod 341)$ ，但 $2^{85} \equiv 32 (\mod 341)$ 。这说明 $341$ 不是质数。

这样检测的准确率很高。随机选择 $k$ 个底数，Miller-Rabin 算法的正确率（不会将合数误判成素数的概率）大于 $1 - 4^{- k}$ 。算法时间复杂度为 $O (k \log^{2} n)$ 。

Miller-Rabin 的效率与选取底数个数有关，我们希望减少底数并保证一定正确性。以下是常用底数，来自 wangrx 的博客。

对 $2^{32}$ 以内的数判素，使用 $2, 7, 61$ 三个底数。
对 $2^{64}$ 以内的数判素，使用 $2, 325, 9375, 28178, 450775, 9780504, 1795265022$ 七个底数。
使用前 $12$ 个素数作为底数可对 $318665857834031151167460 (3 \times 10^{23} \approx 2^{78})$ 以内的数判素。详见 A014233 - OEIS。
固定底数时需特判底数。若以 $2, 7, 61$ 作为底数，则当 $n = 2, 7$ 或 $61$ 时直接通过检验，因为 $p$ 无法通过以 $p$ 为底的费马素性检验。

1.4 复杂度优化

Miller-Rabin 的复杂度和正确性足够优秀，但注意到整个过程中我们多次使用快速幂计算 $a$ 的幂，且指数每次除以 $2$ ，很浪费。

考虑将整个过程反过来，即预先处理好 $p - 1 = r \cdot 2^{d}$ ，计算 $a^{r}$ 并执行 $d$ 次平方操作，即可得到每个 $a^{r \cdot 2^{i}}$ 。时间复杂度优化为 $O (k \log n)$ 。

进一步地，先判掉 $a^{r} \equiv 1 (\mod p)$ ，此时 $p$ 通过检验。否则若 $p$ 是质数，说明在 $i$ 从 $d$ 减小到 $0$ 的过程中， $a^{r \cdot 2^{i}} mod p$ 存在从 $1$ 变为 $- 1$ 的过程，因此只需判断是否存在 $0 \leq i < d$ 使得 $a^{r \cdot 2^{i}} \equiv - 1 (\mod p)$ 。容易证明这是 $p$ 通过本轮素性检验的充要条件。

代码见 2.3 小节 P4718。

2. Pollard-Rho

分解质因数一般使用的试除法时间复杂度为 $O (\sqrt{n})$ ，因为必须枚举到 $\sqrt{n}$ 才能确定 $n$ 为质数。若预先筛出 $\sqrt{n}$ 以内的质数，则复杂度除以 $\log n$ 。

当 $n$ 较小但数据组数 $T$ 较多时，可预先使用线性筛 $O (n)$ 筛出值域内所有数的最小质因子，单次分解质因数 $O (\log n)$ 。

Pollard-Rho 为时间复杂度又开了一次平方，它可以在期望 $\sqrt[4]{n} \log n$ 的时间复杂度内求出 $n$ 的一个非平凡因子，因此使用 Pollard-Rho 分解质因数的时间复杂度为 $\sqrt[4]{n} \log^{2} n$ 。

2.1 生日悖论

从 $1 \sim n$ 的正整数中 $k$ 次等概率随机选择一个数，则所有数互不相同的概率为

P = \frac{n^{\underset{―}{k}}}{n^{k}}

公式含义为从 $n$ 个数中有序选择 $k$ 个互不相同的数的方案数除以总方案数。

直观认知：当 $k$ 增大时， $P$ 衰减很快，因为每次 $\frac{n - k + 1}{n}$ 以相乘的方式作用在 $P$ 上。可以理解为指数衰减，但比指数衰减慢。如下图。

手玩函数图像后，我们发现使得 $P = \frac{1}{2}$ 的 $k$ 似乎是 $\sqrt{n}$ 级别的。

根据 $1 + x \leq e^{x}$ ，可知 $P \leq e^{\sum_{i = 1}^{k} \frac{n - i + 1}{n} - 1} = e^{- \frac{k (k - 1)}{2 n}}$ 。令 $e^{- \frac{k (k - 1)}{2 n}} = \frac{1}{2}$ ，解得 $k$ 在 $\sqrt{n \ln 4}$ 附近。

因此，不严谨地，在 $n$ 个数中等概率随机选择，使得选出的数中存在两个相同的数的期望次数为 $O (\sqrt{n})$ 。

2.2 算法介绍

首先，我们必须有能力快速判断待分解的数是否为质数：Miller-Rabin。

Pollard-Rho 算法的精髓在于构造伪随机函数 $f (x) = x^{2} + c$ 。

因 $f$ 仅含一个变量，故对于相同的 $x$ ， $f (x)$ 的返回值相同。在 $f$ 进入循环前，它不断迭代得到的数可视为随机。其随机性尚未被证明。

根据生日悖论，模 $n$ 意义下，若给定 $c$ 和初始值 $x_{0}$ ，则 $f$ 在不断迭代的过程中期望迭代 $O (\sqrt{n})$ 次进入长度为 $O (\sqrt{n})$ 的循环。一般以 $0$ 作为初始值，则迭代过程形如 $x_{1} = f (x_{0}) = c$ ， $x_{2} = f (x_{1}) = c^{2} + c$ ， $\dots$ ， $x_{i} = f^{i} (x_{0})$ 。

因为整条路径类似希腊字母 $ρ$ ，算法得名 Pollard-Rho，如下图。

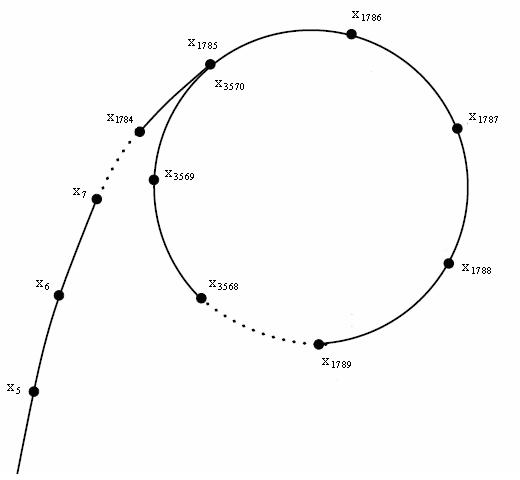
若 $n$ 为合数，则其最小非平凡因子 $m$ 不超过 $\sqrt{n}$ 。因此模 $m$ 意义下期望迭代 $O (\sqrt[4]{n})$ 次进入长度为 $O (\sqrt[4]{n})$ 的循环。

同时，若模 $m$ 一旦进入循环即存在 $x_{i} \equiv x_{j} (\mod m)$ ，即可通过计算 $| x_{i} - x_{j} |$ 和 $n$ 的 $gcd$ 求出 $m$ 或其倍数，前提为 $x_{i} ≢ x_{j} (\mod n)$ ，否则 $gcd$ 结果为 $n$ ，平凡。

记 $x_{i}$ 在模 $n$ 意义下形成的路径为 $ρ_{n}$ ，在模 $m$ 意义下形成的路径为 $ρ_{m}$ 。问题为求出一组 $i, j$ 使得其处于 $ρ_{m}$ 同一点，但处于 $ρ_{n}$ 不同点。这说明 $i$ 需要足够大使得跳出 $ρ_{m}$ 的尾巴，且 $j - i$ 恰好是 $ρ_{m}$ 循环节的倍数。据分析，最小的 $i$ 和 $j$ 的级别均为 $O (\sqrt[4]{n})$ 。

注意，整个过程中我们 不知道 $m$ ，但分析可证求 $m$ 的期望复杂度为 $O (\sqrt[4]{n} \log n)$ 。求得的非平凡因子 $m$ 不一定最小，因此还需继续分解。

考虑从 $i = 1$ 开始计算 $d = gcd (| x_{2 i} - x_{i} |, n)$ 直到该值不等于 $1$ ，此时有两种情况：

$d < n$ ，说明 $d$ 即 $n$ 的非平凡因子，直接返回。
$d = n$ ，说明进入 $ρ_{n}$ 的循环节，大概率因为 $ρ_{n}$ 的环长等于 $ρ_{m}$ 的环长，也可能因为 $ρ_{m}$ 的尾巴过长，使得第一次枚举到 $ρ_{m}$ 环长的倍数使得 $i$ 跳出 $ρ_{m}$ 的尾巴时就枚举到了 $ρ_{n}$ 的环长。无论如何，应结束本次失败的 Pollard-Rho，调整参数 $c$ 重新分解。

上述算法称为基于 Floyd 判环的 Pollard-Rho 算法，期望时间复杂度 $O (\sqrt[4]{n} \log n)$ 。

注意：笔者实现 Floyd 判环后，发现若令 $d = gcd (| x_{2 i} - x_{i} |, n)$ 则 $n = 4$ 无论 $c$ 取何值均无法分解。需要特判 $n = 4$ 或从 $i = 0$ 开始计算 $d = gcd (| x_{2 i + 1} - x_{i} |, n)$ 。
优化： $gcd$ 次数过多降低效率。朴素 Floyd 判环法无法通过模板题。考虑设置 样本累计上限 $T$ ，将 $T$ 组 $gcd$ 测试打包，将常数减小 $T$ 倍。 $T = 10$ 在模板题数据下表现优秀。其正确性基于 $gcd (a, n) ∣ gcd (a b mod n, n)$ 。
优化：二分未知上界的数的最好方法是倍增。 $n$ 较大时 $T = 10$ 太小了。考虑每检查一次就将 $T$ 乘以 $2$ 。同时为防止 $T$ 过大无法及时检查，令 $T$ 对 $C$ 取较小值。一般取 $C = 127$ 。

如果读者担心 $n$ 较小时算法的正确性，可预处理答案。读者需要认识到 PR 本身是随机性算法的事实，没有绝对正确的写法，只有效率和正确性相对优秀的写法。对于广为流传的 PR 写法，前人已经验证其在一定范围内的正确性，可放心大胆使用。

总之， $d$ 的计算方式多种多样，但样本累计优化不可少。检查太耗时则打包，这样的思想不仅可用于优化 Pollard-Rho，也可以应用在其它领域。

2.3 例题

P4718【模板】Pollard-Rho 算法

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
ll rd(ll l, ll r) {return rnd() % (r - l + 1) + l;}
ll ksm(ll a, ll b, ll p) {
  ll s = 1;
  while(b) {
    if(b & 1) s = (__int128) s * a % p;
    a = (__int128) a * a % p, b >>= 1;
  }
  return s;
}
bool Miller(ll n) {
  if(n < 3 || n % 2 == 0) return n == 2;
  ll r = n - 1, d = 0;
  while(r & 1 ^ 1) r >>= 1, d++;
  for(int _ = 0; _ < 10; _++) {
    ll a = rd(2, n - 1), v = ksm(a, r, n);
    if(v == 1) continue;
    for(int i = 0; i <= d; i++) {
      if(i == d) return 0;
      if(v == n - 1) break;
      v = (__int128) v * v % n;
    }
  }
  return 1;
}
ll Pollard(ll n) {
  ll c = rd(1, n - 1), s = c, t = 0;
  auto f = [&](ll x) {return ((__int128) x * x + c) % n;};
  ll acc = 0, prod = 1, d, limit = 1;
  while(s != t) {
    prod = (__int128) prod * abs(s - t) % n;
    if(++acc == limit) {
      if((d = __gcd(prod, n)) > 1) return d;
      acc = 0, limit = min(127ll, limit << 1);
    }
    s = f(f(s)), t = f(t);
  }
  if((d = __gcd(prod, n)) > 1) return d;
  return n;
}
ll mxp(ll n) {
  if(Miller(n)) return n;
  if(n == 1) return 1;
  ll d = Pollard(n);
  while(d == n) d = Pollard(n);
  while(n % d == 0) n /= d;
  return max(mxp(d), mxp(n));
}
int main() {
  ios::sync_with_stdio(0);
  ll T, n;
  cin >> T;
  while(T--) {
    cin >> n;
    if(Miller(n)) cout << "Prime\n";
    else cout << mxp(n) << "\n";
  }
  return 0;
}