树状数组的妙用

作为一个常数非常小且非常好写的数据结构，树状数组（Binary Index Tree, BIT）自然受到了很多选手的青睐。除了众所周知的区间加区间求和，树状数组还能代替常数巨大的线段树做不少事情，如维护高维差分或在 BIT 上二分，是卡常的不二选择。

本篇文章主要介绍最近碰到的树状数组维护高维差分和 BIT 二分。以后碰到更多用法的时候会更新。

1. BIT 二分（倍增）

CSPS 2021 前学习一下，感觉会用到。

树状数组的树形结构决定了它可以倍增的性质。实际上，BIT 就是省略了右儿子的线段树，因此线段树的功能完全包含 BIT，但为此付出的代价是 \(2\sim 10\) 倍的常数。将 BIT 的树状结构牢记于心，可以更好理解 BIT 倍增：

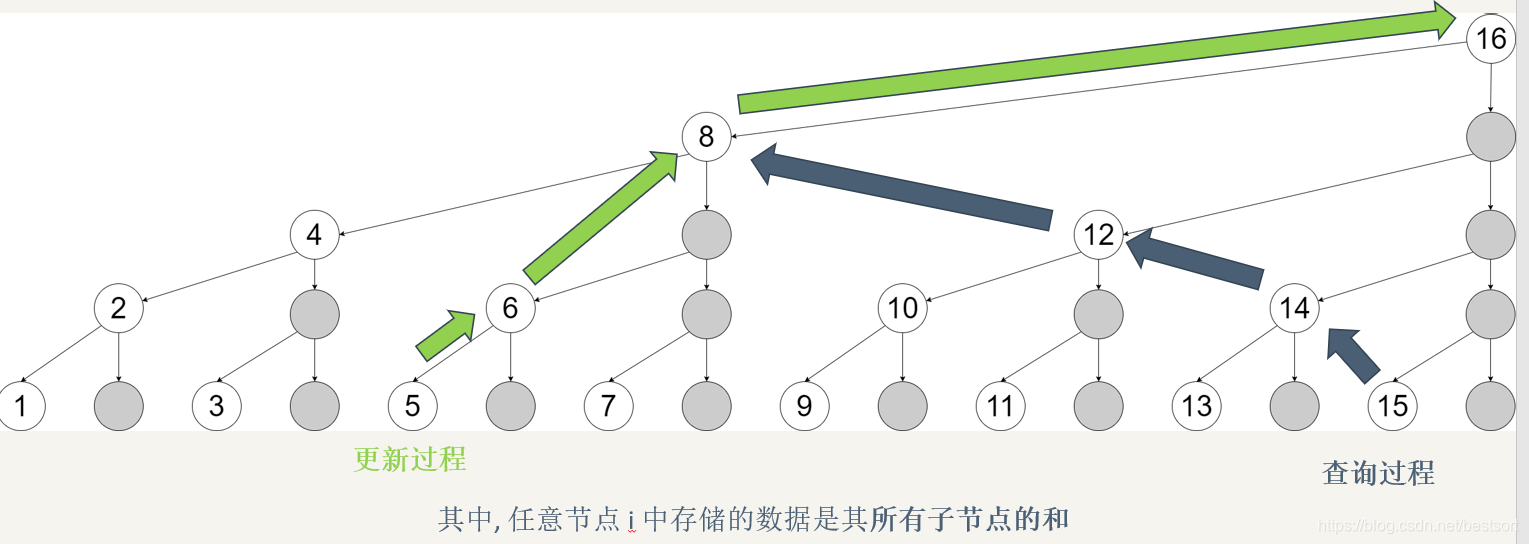
下标为 \(p\) 的位置存储着 \([l,p]\) 的信息和，其中 \(l=p-2^{\mathrm{lowbit}(p)}+1\)，其长度为 \(p-l+1=2^{\mathrm{lowbit}(p)}\)，这给予我们倍增的条件。具体流程如下：

维护一个信息前缀和 \(cur\) 与当前位置 \(p\)，从大到小枚举 \(2^k\leq n\)，若 \(p+2^k\leq n\) 且 \(cur+\mathrm{Information}(p+2^k)\) 符合条件，则令 \(p\gets p+2^k\)，否则不变。最终得到的 \(p\) 一定是最大且符合条件的位置。

为什么这样可以呢，注意到如果我们给 \(p\) 加上 \(2^k\) 满足 \(k<\mathrm{lowbit}(p)\)，则 \(\mathrm{Information}(p+2^k)\) 实际上维护了 \([p+1,p+2^k]\) 的信息和（显然 \(\mathrm{lowbit}(p+2^k)=k\)），故算法正确。

当然，这样的倍增所适用的信息仍然局限于 BIT 可以维护的信息范围内，不过一般来说 \(\mathrm{sum}\) 已经足以应付大多数题目了。来看几道例题。

I. P6619 [省选联考 2020 A/B 卷] 冰火战士

太经典了。

首先将温度离散化，那么我们就是要找冰系战士能力关于温度的前缀和与火系战士能力的后缀和在某个温度处较小值的最大值。由于能力都是正整数因此前缀和单调递增，后缀和单调递减，考虑用树状数组维护冰火战士能力前缀和（后缀和等于总和减去前缀和）然后二分找到最大的 \(p\) 使得 \(\mathrm{Icesum}_p\leq\mathrm{Firetotal}-\mathrm{Firesum}_{p-1}\)，以及最大的 \(p\)（这个温度要求最大就挺麻烦）使得 \(\mathrm{Icesum}_p\geq \mathrm{Firetotal}-\mathrm{Firesum}_{p-1}\) 且 \(\mathrm{Icesum}_p\) 最小，两者对比取更优解即可。

时间复杂度 \(\mathcal{O}(n\log n)\)。通过卡常拿到了最优解（10.23）。

const int N = 2e6 + 5;

int n, lg, cnt, d[N], op[N], t[N], x[N], y[N];
int c1[N], c2[N], Fire;
void add(int x, int v, int *c) {while(x <= cnt) c[x] += v, x += x & -x;}
void query() {
	int p = 0, v1 = 0, v2 = 0;
	for(int i = lg; ~i; i--) {
		int np = p + (1 << i);
		if(np <= cnt && v1 + c1[np] <= Fire - c2[np] - v2)
			p = np, v1 += c1[p], v2 += c2[p];
	}
	if(p < cnt) {
		int x = p + 1, w1 = 0, w2 = 0;
		while(x) w1 += c1[x], w2 += c2[x], x -= x & -x;
		if(v1 <= min(w1, Fire - w2)) {
			v1 = w1, v2 = w2, p = 0;
			for(int i = lg, w2 = 0; ~i; i--) {
				int np = p + (1 << i);
				if(np <= cnt && w2 + c2[np] <= v2) w2 += c2[p = np];
			}
		}
	}
	int ans = min(v1, Fire - v2);
	if(ans) print(d[p]), pc(' '), print(ans << 1), pc('\n');
	else pc('P'), pc('e'), pc('a'), pc('c'), pc('e'), pc('\n');
}

int main(){
	n = read(), lg = log2(n);
	for(int i = 1; i <= n; i++) {
		op[i] = read(), t[i] = read();
		if(op[i] == 1) d[i] = x[i] = read(), y[i] = read();
	} sort(d + 1, d + n + 1), cnt = unique(d + 1, d + n + 1) - d - 1;
	for(int i = 1; i <= n; i++) {
		if(op[i] == 1) {
			x[i] = lower_bound(d + 1, d + cnt + 1, x[i]) - d;
			if(t[i] == 1) Fire += y[i], add(x[i] + 1, y[i], c2);
			else add(x[i], y[i], c1);
		} else {
			int p = t[i];
			if(t[p] == 1) Fire -= y[p], add(x[p] + 1, -y[p], c2);
			else add(x[p], -y[p], c1);
		} query();
	}
    return flush(), 0;
}

II. 2021NOIP 联考 石室中学 T3 集合

题意简述：维护一个数堆 \(a_i\)，支持插入一个数或询问 \(c\)，求出最多进行多少次选出 \(c\) 个数并减去 \(1\)。

\(1\leq a_i\leq 10^9\)，\(1\leq n\leq 10^6\)。

一个比较显然的想法是每次选出最大的 \(c\) 个数减去 \(1\)（赛时只想到了这一点）。

有这样一个结论：找出最大的数 \(v\) 以及剩下数的和 \(s\)，若 \(v>\dfrac s {c-1}\)，则 \(v\) 每次必然被选，令 \(c\gets c-1\) 并丢掉 \(v\)。否则 \(v\leq \dfrac{s}{c-1}\)，每次操作后仍然满足这个关系，因此答案就是 \(\dfrac{s+v}{c}\)。

如果将所有数从大到小排序，我们就是要找最后一个位置 \(i\) 使得 \(a_i> \dfrac{\mathrm{suffixsum}_{i+1}}{c-i}\)，稍做变形得到 \(c> \dfrac{\mathrm{suffixsum}_{i+1}}{a_i}+i\)。注意到不等号右边的柿子两部分在任何时候都是随着 \(i\) 增加而（非）严格递增的，因此若 \(i\) 满足要求，则任意 \(j<i\) 都满足要求，满足可二分性。同时增加一个数相当于后缀加，可以 BIT 维护，故使用 BIT 倍增。

具体地，我们倍增找到最靠右的位置 \(p\) 使得 \(c>\dfrac{\mathrm{suffixsum}_{p+1}}{a_p}+p\)，那么 \(\dfrac{\mathrm{totalsum} - \mathrm{prefixsum}_p}{c-p}\) 就是答案。时间复杂度 \(\mathcal{O}(n\log n)\)。

const int N = 1e6 + 5;
int n, u, q, lg, rk[N], qu[N];
ll cnt[N], sum[N];
pii a[N];

int main() {
	cin >> n, lg = log2(n);
	for(int i = 1; i <= n; i++) {
		int op = read();
		if(op == 1) a[++u] = {read(), i};
		else qu[++q] = read();
	}
	sort(a + 1, a + u + 1, [&](pii x, pii y) {return x.fi > y.fi;});
	for(int i = 1; i <= u; i++) rk[a[i].se] = i;
	for(ll i = 1, p = 0, q = 0, tot = 0; i <= n; i++) {
		if(rk[i]) {
			int x = rk[i], v = a[x].fi; q++, tot += v;
			while(x <= u) cnt[x]++, sum[x] += v, x += x & -x;
		} else {
			ll c = qu[++p], x = 0;
			ll csum = 0, ccnt = 0;
			for(int i = lg; ~i; i--) {
				ll nx = x + (1 << i);
				if(nx > n) continue;
				ll v = a[nx].fi;
				ll nsum = csum + sum[nx];
				ll ncnt = ccnt + cnt[nx];
				if(ncnt >= c) continue;
				if(c * v > tot - nsum + ncnt * v)
					x = nx, csum = nsum, ccnt = ncnt;
			}
			print((tot - csum) / (c - ccnt)), pc('\n'); 
		}
	}
	return flush(), 0;
}