树状数组进阶
推荐在 cnblogs 阅读。
作为一个常数小且好写的数据结构,树状数组(Binary Indexed Tree,BIT)是求解数据结构问题的第一选择。
除了众所周知的区间加区间求和,树状数组还能代替常数巨大的线段树做很多事情,例如树状数组二分和维护高维差分。
1. 树状数组的结构
很多选手对树状数组的了解仅停留在背诵层面,却不知道这短短的两行代码背后的实际含义。深入研究树状数组的结构有助于我们更好地理解和运用树状数组。
- 树状数组可以看做线段树的简化版本,这样的简化使得它只支持前缀(或后缀)查询。因此,用树状数组维护的信息一般需要具有可减性。若信息没有可减性,则要求查询前后缀,或转化为查询前后缀。
考虑最基本的问题:单点加,单点求前缀和。设序列为
树状数组的核心思想在于,将一次前缀查询
1.1 区间拆分
对于任意正整数
同样的,对于区间
考虑
这样拆分有一个非常好的性质:对于每个右端点
这说明不同的子区间总数 恰好为
1.2 查询与修改
对于查询
接下来一大篇全部是关于修改的。
分析所有包含
考虑
这是合法的例子(
这是不合法的例子:
第一个例子因为
根据条件,我们可以直接构造所有
例如,对于
可以很明显地看出,对于
我们令
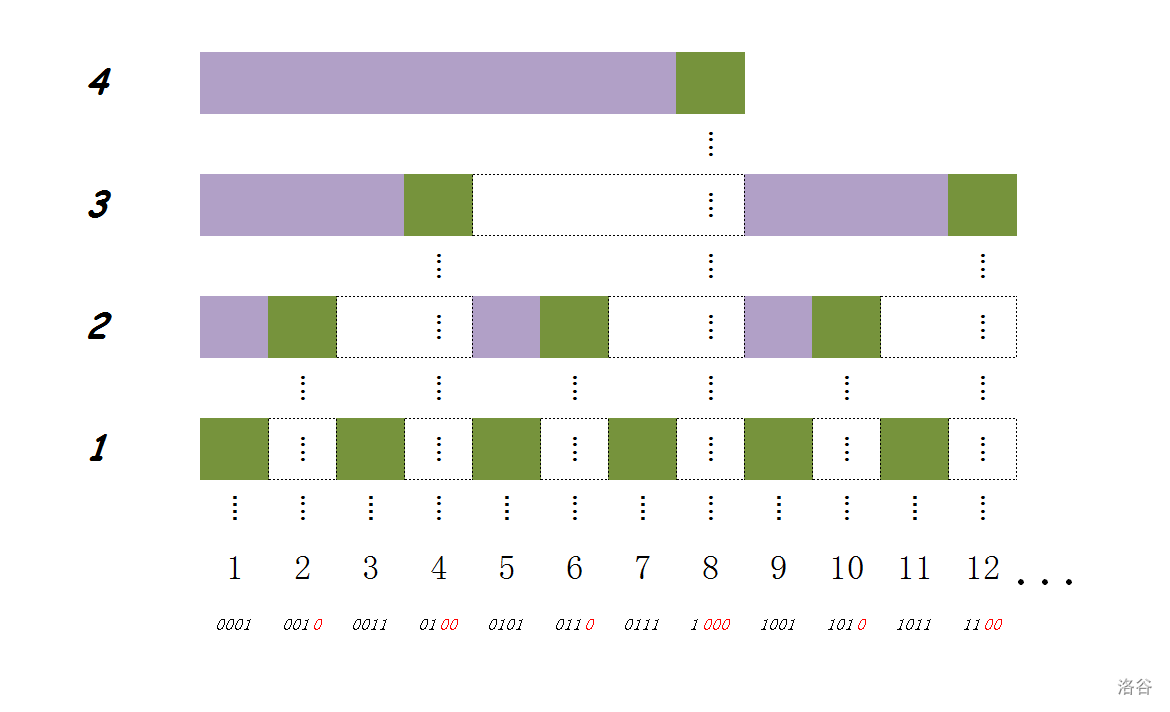
综上,对于修改
将修改和查询放在一起看,再来一张图加深印象(图源):
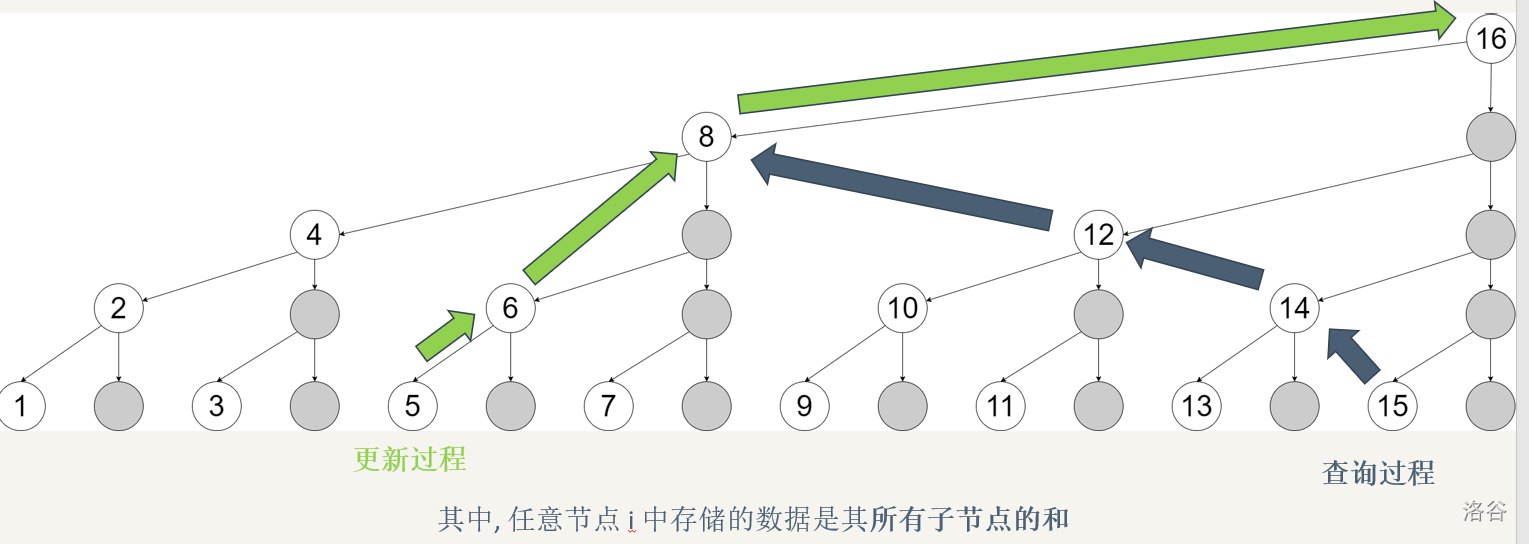
实际上,我们可以将树状数组看成 省略了所有右儿子的线段树。
从另一种角度也可以推导出上述结果:尝试证明所有区间包含或相离。满足条件的区间集合可以建树,求出每个区间的父亲,即包含该区间的长度最小的区间对应右端点编号。具体细节留给感兴趣的读者自行补充。
1.3 求
用预处理
计算机用补码存储和表示数值。考虑
例如,对于二进制数 x & -x。
这样,我们可以顺利成章地写出支持 模板题 操作的树状数组了。
int n, c[N];
void add(int x, int v) {while(x <= n) c[x] += v, x += x & -x;}
int query(int x) {int s = 0; while(x) s += c[x], x -= x & -x; return s;}
int query(int l, int r) {return query(r) - query(l - 1);} // 区间查询转化为两次前缀查询.
1.4 树状数组二分
类似线段树二分,树状数组也可以二分。只要理解了树状数组的结构,就很容易理解树状数组二分。
它可以抽象成这样一类问题:存在分割点
考虑查询最后一个前缀和
树状数组二分的本质是 倍增。设当前位置为
最终
1.5 例题
P6619 [省选联考 2020 A/B 卷] 冰火战士
太经典了。
首先将温度离散化,就是求冰系战士能力关于温度的前缀和,与火系战士能力的后缀和在某个温度处较小值的最大值。由于能力都是正整数,所以前缀和单调递增,后缀和单调递减,考虑用树状数组维护冰火战士能力关于温度的前缀和(后缀和等于总和减去前缀和)。
每次查询二分找到最大的
时间复杂度
P4602 [CTSC2018] 混合果汁
整体二分,则问题相当于将所有美味度不小于当前二分值的果汁拎出来,按单价从小到大排序,求买
注意在每次
使用 BIT 倍增,时间复杂度
P3586 [POI2015] LOG
每次贪心选最大的
每个数之间顺序无关,一般通过排序寻找性质:对于最大的元素
证明:看成一个
判断是否有
时间复杂度
[模拟赛] 集合
维护初始为空的序列
,支持插入一个数或询问 ,求出最多进行多少次选出 个数并减去 。
, 。2s,512MB。
和上一题(P3586)思想差不多,但是稍微难一点。
考虑哪些元素每次必然被选,自然从最大值开始考虑。设最大值为
将所有数从大到小排序,相当于找到最后一个位置使得
证明:变形得
离散化 + BIT 二分找到最后一个满足条件的位置,则
时间复杂度
2. 对树状数组的理解
上面讨论的都是前缀 BIT,前缀表示查询一段前缀。它本质上是 一阶前缀和:在
对于单点加区间求和,转化为 “单点修改原序列” 对 “某个位置的前缀和” 的贡献:给
对于区间加单点查询,转化为 “单点修改差分序列” 对 “原序列的某个位置” 的贡献:给
2.1 高阶前缀和
当问题来到高阶前缀和,应当如何去思考?简单,只需要梳理清楚某处修改对某处查询的贡献即可。
对于区间加区间求和,转化为 “单点修改差分序列” 对 “某个位置的前缀和” 的贡献。这是二阶前缀和。
考虑给
换言之,我们考虑 单次修改对单次查询的贡献。对于某种维护方式,只要单次修改对单次查询的答案是对的,那么无论多少次修改,多少次查询,它依然正确。
支持线段树 模板题 操作(区间加,区间求和)的树状数组如下:
using ll = long long;
ll n, c[N], c2[N];
void add(int x, ll v) {
ll v2 = 1ll * x * v;
while(x <= n) c[x] += v, c2[x] += v2, x += x & -x;
}
void add(int l, int r, ll v) {add(l, v), add(r + 1, -v);}
ll query(int x) {
ll y = x + 1, s = 0, s2 = 0;
while(x) s += c[x], s2 += c2[x], x -= x & -x;
return s * y - s2;
}
ll query(int l, int r) {return query(r) - query(l - 1);}
对于更高阶前缀和,思路是一致的。
假设
对组合数较熟悉的同学已经发现,矩阵第
综上,对于
例如,当
- 求出
- 求出
- 求出
将上述三个结果相加即为所求。
时间复杂度
2.2 二维 BIT
本质上是树状数组套树状数组,用二维数组维护。它可以直接做单点加矩形查询,且矩形两维的左边界都是
对于矩形加矩形求和,即维护二维差分数组的二阶二维前缀和。类似地,考虑
时间复杂度
模板题 代码:
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2050;
char s;
int n, m, c1[N][N], c2[N][N], c3[N][N], c4[N][N];
void add(int x, int y, int v) {
int v2 = x * v, v3 = y * v, v4 = x * y * v;
for(int i = x; i <= n; i += i & -i)
for(int j = y; j <= m; j += j & -j)
c1[i][j] += v, c2[i][j] += v2, c3[i][j] += v3, c4[i][j] += v4;
}
int query(int x, int y) {
int s1 = 0, s2 = 0, s3 = 0, s4 = 0;
for(int i = x; i; i -= i & -i)
for(int j = y; j; j -= j & -j)
s1 += c1[i][j], s2 += c2[i][j], s3 += c3[i][j], s4 += c4[i][j];
return (x + 1) * (y + 1) * s1 - (y + 1) * s2 - (x + 1) * s3 + s4;
}
int main() {
cin >> s >> n >> m;
while(cin >> s) {
if(s == 'L') {
int a, b, c, d, v;
cin >> a >> b >> c >> d >> v;
add(a, b, v), add(c + 1, b, -v), add(a, d + 1, -v), add(c + 1, d + 1, v);
}
else {
int a, b, c, d;
cin >> a >> b >> c >> d;
cout << query(c, d) + query(a - 1, b - 1) - query(a - 1, d) - query(c, b - 1) << "\n";
}
}
return 0;
}
2.3 后缀 BIT
交换查询和修改的跳转方式就是后缀 BIT 了。
int n, c[N];
void add(int x, int v) {while(x) c[x] += v, x -= x & -x;}
int query(int x) {int s = 0; while(x <= n) s += c[x], x += x & -x; return s;}
int query(int l, int r) {return query(l) - query(r + 1);}
可以这样思考:在前缀 BIT 中,对于
对于可减信息,用前缀后缀 BIT 维护是一样的。后缀 BIT 的用途在于,当信息不可减且询问具有良好性质(询问后缀,或可以转化为询问后缀)时,能够不翻转序列地维护修改和查询,避免因翻转序列产生的大量下标变换使得代码写挂。
参考资料
第一章




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!