线段树进阶 Part 1

线段树是信息学竞赛最常见的数据结构。本篇笔记总结技巧和应用，不介绍基本线段树算法。

1. 常见技巧

1.1 信息设计

用线段树解决问题，首先得考虑维护哪些信息。若不带修，任何 满足结合律且封闭 的信息（称为半群）都是可维护的。结合律一般都有，封闭性帮助我们设计信息。

例如区间最大子段和，显然要维护最大子段和。封闭性要求从 $[l, m]$ 和 $[m + 1, r]$ 的信息推出 $[l, r]$ 。若仅维护最大子段和 $a n s$ ，合并时取子区间的最大子段和的较大值，则得到左子区间或右子区间的最大子段和，这忽略了左端点在 $[l, m]$ 且右端点在 $[m + 1, r]$ 的区间。跨过中点的最大区间是 $[l, m]$ 的最大后缀与 $[m + 1, r]$ 的最大前缀拼在一起，于是维护区间最大前后缀和 $p r e, s u f$ ，这样就能从子区间的信息得到当前区间的最大子段和。

那么最大前后缀和怎么从子区间合并？考虑到前缀是左子区间的某个前缀，或者整个左子区间接上右子区间的前缀，所以还要维护整个区间的和 $s u m$ 。对于最大后缀和同理。此时信息已经封闭：区间和等于子区间的区间和相加。

\begin{aligned} a n s & \leftarrow max (a n s_{l s}, a n s_{r s}, s u f_{l s} + p r e_{r s}) \\ p r e & \leftarrow max (p r e_{l s}, s u m_{l s} + p r e_{r s}) \\ s u f & \leftarrow max (s u f_{r s}, s u f_{l s} + s u m_{r s}) \\ s u m & \leftarrow s u m_{l s} + s u m_{r s} \end{aligned}

从上例感受设计信息的流程：从要求的答案开始，考虑答案如何从子区间的答案合并。为此，可能需要维护一些辅助信息。再考虑辅助信息如何由子区间的辅助信息合并。重复该过程直到信息封闭。这种略显机械性的方法比一下子想出所有要维护的信息更简单。

对于懒标记，同样需要满足结合律和封闭性。不用满足交换律，因为及时 push_down 保证每次打懒标记都是将当前懒标记对应的操作序列接在原懒标记对应的操作序列之后，即我们按时间顺序处理所有懒标记。

区间修改时，不仅标记和信息各自封闭，还要求标记和信息之间相互配合，使得原信息根据懒标记能够快速计算新的信息。因此，区间修改相较单点修改可能需要维护更多信息。

1.2 抽象线段树

当所维护信息太多时，用结构体会更有条理。此时一个结构体就是半群上的一个元素，我们只需考虑如何合并两个结构体。同样地，对于区间修改，可以用另一类结构体表示标记。

这其实抽象出了线段树的运作框架：用线段树解决区间修改的区间半群和，就是考虑时间相邻的标记如何合并，下标相邻的信息如何合并，以及标记如何作用在信息上，最终得到一棵 “抽象线段树”（第一次听到这个概念是在 APIO2022 的讲课上，感兴趣的读者可以翻翻 lxl 的课件），而标记和信息长成什么样和具体问题有关。从这个角度考虑线段树，可以让我们思考问题更有条理，尤其是当问题很复杂的时候，例如下一小节的历史和。

1.3 维护历史信息

线段树维护区间修改的区间历史信息涉及复杂的标记与信息的设计和合并。

1.3.1 历史最值

我们以经典老题 CPU 监控为例，分析历史最值问题的一般思路。题目要求支持区间加区间赋值，查询区间当前最大值和历史最大值。

第一步：信息设计

显然维护当前最大值 $m x$ 和历史最大值 $h$ ，此时信息已经封闭：

\begin{aligned} m x & \leftarrow max (m x_{l s}, m x_{r s}) \\ h & \leftarrow max (h_{l s}, h_{r s}) \end{aligned}

这一步讨论了信息的合并。

第二步：标记设计

首先少不了区间加区间赋值的经典标记。如果被赋值过，那么维护赋的值 $a s$ ，否则维护加的值 $a d$ 。赋值 $a s$ 之后加上 $a d$ 等价于赋值 $a s + a d$ ，所以要么只有 $a s$ 标记，要么只有 $a d$ 标记。

维护 $a s$ 和 $a d$ 用于更新 $m x$ ：如果有 $a s$ 标记，那么 $m x \leftarrow a s$ ，否则 $m x \leftarrow m x + a d$ 。更新 $h$ 需要哪些标记呢？

我们要求一段操作之后的历史最大值。以第一次赋值为分界线，之前的操作都是加法，之后的操作都是赋值。这两种操作需要分开考虑，因为加的值和赋的值显然不能混为一谈。于是维护加法操作前缀和（加法累计，而赋值不累计）的历史最大值 $h_{a d}$ ，以及赋值操作的历史最大值 $h_{a s}$ 。那么新的历史最大值 $h \leftarrow max (h, m x + h_{a d}, h_{a s})$ 。

这一步讨论了标记如何作用在信息上。

第三步：标记合并

不用动脑子的方法是分成两个具有先后关系的标记是否有 $a s$ 标记的四种情况讨论，根据实际意义合并。

如果两个都没有 $a s$ 标记：

\begin{aligned} a d & \leftarrow a d_{l} + a d_{r} \\ h_{a d} & \leftarrow max (h_{a d_{l}}, a d_{l} + h_{a d_{r}}) \end{aligned}

如果只有 $l$ 有 $a s$ 标记：

\begin{aligned} a s & \leftarrow a s_{l} + a d_{r} \\ h_{a d} & \leftarrow h_{a d_{l}} \\ h_{a s} & \leftarrow max (h_{a s_{l}}, a s_{l} + h_{a d_{r}}) \end{aligned}

如果只有 $r$ 有 $a s$ 标记：

\begin{aligned} a s & \leftarrow a s_{r} \\ h_{a d} & \leftarrow max (h_{a d_{l}}, a d_{l} + h_{a d_{r}}) \\ h_{a s} & \leftarrow h_{a s_{r}} \end{aligned}

如果两个都有 $a s$ 标记：

\begin{aligned} a s & \leftarrow a s_{r} \\ h_{a d} & \leftarrow h_{a d_{l}} \\ h_{a s} & \leftarrow max (h_{a s_{l}}, a s_{l} + h_{a d_{r}}, h_{a s_{r}}) \end{aligned}

动脑子的方法是通过合理设置空值避免分类讨论。这样虽然代码量少，但是容易出错。

这一步讨论了标记的合并。过程中可能会为了标记的封闭性要求维护更多标记。

把讨论好的东西套在线段树的框架上实现即可。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int N = 1e5 + 5;
constexpr ll inf = 1e18;
ll n, m, a[N];
struct tag {
  ll ad, as, had, has;
  tag operator + (const tag &z) const { // 标记合并
    tag res;
    if(as == -inf && z.as == -inf) {
      res.ad = ad + z.ad;
      res.as = -inf;
      res.had = max(had, ad + z.had);
      res.has = -inf;
    }
    if(as == -inf && z.as != -inf) {
      res.ad = 0;
      res.as = z.as;
      res.had = max(had, ad + z.had);
      res.has = z.has;
    }
    if(as != -inf && z.as == -inf) {
      res.ad = 0;
      res.as = as + z.ad;
      res.had = had;
      res.has = max(has, as + z.had);
    }
    if(as != -inf && z.as != -inf) {
      res.ad = 0;
      res.as = z.as;
      res.had = had;
      res.has = max(has, max(as + z.had, z.has));
    }
    return res;
  }
} laz[N << 2];
struct dat {
  ll his, mx;
  dat operator + (const dat &z) const { // 信息合并
    return {max(his, z.his), max(mx, z.mx)};
  }
  dat operator + (const tag &z) const { // 标记作用在信息上
    return {max(his, max(mx + z.had, z.has)), z.as == -inf ? mx + z.ad : z.as};
  }
} val[N << 2];
void build(int l, int r, int x) {
  if(l == r) {
    val[x] = {a[l], a[l]};
    return;
  }
  int m = l + r >> 1;
  build(l, m, x << 1);
  build(m + 1, r, x << 1 | 1);
  val[x] = val[x << 1] + val[x << 1 | 1];
  laz[x] = {0, -inf, 0, -inf};
}
void adtag(int x, tag v) {
  val[x] = val[x] + v;
  laz[x] = laz[x] + v;
}
void down(int x) {
  adtag(x << 1, laz[x]);
  adtag(x << 1 | 1, laz[x]);
  laz[x] = {0, -inf, 0, -inf}; // 注意清空标记
}
void modify(int l, int r, int ql, int qr, int x, tag v) {
  if(ql <= l && r <= qr) return adtag(x, v);
  int m = l + r >> 1;
  down(x);
  if(ql <= m) modify(l, m, ql, qr, x << 1, v);
  if(m < qr) modify(m + 1, r, ql, qr, x << 1 | 1, v);
  val[x] = val[x << 1] + val[x << 1 | 1];
}
dat query(int l, int r, int ql, int qr, int x) {
  if(ql <= l && r <= qr) return val[x];
  int m = l + r >> 1;
  down(x);
  dat res = {-inf, -inf};
  if(ql <= m) res = res + query(l, m, ql, qr, x << 1);
  if(m < qr) res = res + query(m + 1, r, ql, qr, x << 1 | 1);
  return res;
}
int main() {
  cin >> n;
  for(int i = 1; i <= n; i++) cin >> a[i];
  build(1, n, 1);
  cin >> m;
  for(int i = 1; i <= m; i++) {
    char op;
    cin >> op;
    int x, y, z;
    if(op == 'A') cin >> x >> y, cout << query(1, n, x, y, 1).his << "\n";
    if(op == 'Q') cin >> x >> y, cout << query(1, n, x, y, 1).mx << "\n";
    if(op == 'P') cin >> x >> y >> z, modify(1, n, x, y, 1, {z, -inf, max(0, z), -inf});
    if(op == 'C') cin >> x >> y >> z, modify(1, n, x, y, 1, {0, z, 0, z});
  }
  return 0;
}

1.3.2 历史和

历史和问题和历史最值问题的求解思路类似，需要在标记里多维护一个求历史和轮数。

考虑区间加区间历史和。信息维护区间长度 $l e n$ ，区间和 $s$ 以及区间历史和 $h$ ，标记维护每个位置加的值 $d s$ 。 $s$ 通过 $d s$ 和 $l e n$ 维护（区间加区间和基本操作），考虑 $h$ 。

设每次求历史和的时候加的值分别为 $d s_{1}, \dots, d s_{t}$ ，则历史和新增

\sum_{i = 1}^{t} (s + l e n \cdot d s_{i}) = s \cdot t + l e n \cdot \sum_{i = 1}^{t} d s_{i}

于是标记维护 每个位置 加的值的历史和 $h s = \sum_{i = 1}^{t} d s_{i}$ ，以及求历史和轮数 $t$ 。一般会让 $t$ 单独加 $1$ 表示求一轮历史和。标记作用在 $h$ 上： $h \leftarrow h + s \cdot t + l e n \cdot h s$ 。

根据实际意义合并标记： $d s$ 和 $t$ 简单相加， $h s = h s_{l} + d s \cdot t + h s_{r}$ 。

例题：P8868。

1.3.3 矩阵乘法与历史和

前置知识：矩阵乘法。

设区间长度 $l e n$ ，区间和 $s$ ，区间历史和 $h$ 。整体加 $v$ 是 $s \leftarrow s + v \cdot l e n$ ，求历史和是 $h \leftarrow h + s$ ，都是 $l e n, s, h$ 的线性组合。将一些数的每个数同时变成所有数的线性组合，我们立刻想到向量和矩阵乘法。

将信息写成行向量 $[\begin{matrix} l e n & s & h \end{matrix}]$ ，则整体加 $v$ 等价于右乘矩阵

[\begin{matrix} l e n & s & h \end{matrix}] \times [\begin{matrix} 1 & v & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] = [\begin{matrix} l e n & s + v \cdot l e n & h \end{matrix}]

求 $t$ 次历史和等价于右乘矩阵

[\begin{matrix} l e n & s & h \end{matrix}] \times [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & t \\ 0 & 0 & 1 \end{matrix}] = [\begin{matrix} l e n & s & h + t \cdot s \end{matrix}]

矩阵乘法满足结合律，可以用线段树维护区间向量乘矩阵，区间向量和。模拟矩阵乘法可知任何标记的主对角线元素为 $1$ ，且左下角为 $0$ 。标记形如

[\begin{matrix} 1 & d s & h s \\ 0 & 1 & t \\ 0 & 0 & 1 \end{matrix}]

与上一小节 $h \leftarrow h + t \cdot s + h s \cdot l e n$ 的线性组合式一致，可知两者本质相同。矩阵法的思维难度较低，但常数大，因为进行了一些无用乘法。变量法给矩阵的每个位置赋予实际含义，抓住了矩阵主对角线及下方恒定的性质。从实际意义理解：区间长度恒定，和贡献至历史和，而历史和不会贡献至和。

1.4 动态开点

当线段树数量太多（线段树合并）或下标值域太大（权值线段树）时，由于空间限制，无法使用左儿子两倍，右儿子两倍加一的编号方法。

解决方法是 动态开点：对于每个结点，维护其左右儿子的编号，向下递归时，若当前结点为空则新建结点。查询时走到空结点就返回。

一般通过 传递引用 或 返回结点编号 的方式快速更新子结点编号。

以下是一个单点修改，区间求和的动态开点线段树实现。相比普通线段树，动态开点线段树向下递归时不再是 x << 1 / x << 1 + 1 而是 ls[x] / rs[x]。

void modify(int l, int r, int p, int &x, int v) {
  if(!x) x = ++node; // 如果结点为空，就新建一个
  if(l == r) return val[x] = v, void();
  int m = l + r >> 1;
  if(p <= m) modify(l, m, p, ls[x], v);
  else modify(m + 1, r, p, rs[x], v);
  val[x] = val[ls[x]] + val[rs[x]];
}
int query(int l, int r, int ql, int qr, int x) {
  if(!x || ql <= l && r <= qr) return val[x]; // 走到空结点返回 val[0] = 0
  int m = l + r >> 1, ans = 0;
  if(ql <= m) ans += query(l, m, ql, qr, ls[x]);
  if(m < qr) ans += query(m + 1, r, ql, qr, rs[x]);
  return ans;
}

1.5 标记永久化

众所周知，线段树的区间修改需要打懒标记。但部分线段树下传懒标记的代价过大，或不支持下传懒标记。例如可持久化线段树和动态开点线段树，下传懒标记需要新建结点，空间常数大。又例如树套树，无法下传懒标记。此时有 标记永久化 的技巧：按着懒标记不下传，查询时，考虑从根到当前区间的路径上每个点的懒标记。

以区间取最大值，区间最大值为例，对每个区间维护两个信息，一是 $v a l$ 表示不考虑该区间所有祖先的懒标记时的子树最大值，二是 $l a z$ 表示当前区间的懒标记的最大值。每个区间的真实值为它的 $v a l$ 与从根到当前区间的路径 $P$ 上所有结点的 $l a z$ 的最大值，因为能够下传懒标记到当前区间的所有点恰好为 $P$ 。

注意：如果使用 push_up 的方式维护 $v a l$ ，根据实际意义， $v a l (x) = max (v a l (l s_{x}), v a l (r s_{x}), l a z (x))$ 。

我们探究什么样的 “信息-标记” 二元组可标记永久化。

在查询过程中，我们按照从根到当前区间的顺序合并懒标记信息，与这些标记被打上的时刻顺序不同。例如三次修改 $a, b, c$ ， $a$ 和 $c$ 打在根上， $b$ 打在根的左儿子上。查询信息时表现出的修改顺序是 $a, c, b$ 。因此，修改必须 顺序无关，即标记具有 交换律。

在原线段树的基础上满足这个条件，结合 push_up，就可以用标记永久化做区间修改，区间查询了。

区间赋值和修改顺序相关，可维护时间戳转化为求时间戳最值。
如果无法 push_up，则需要更强的条件。见 4.2 小节线段树套线段树。

例题：SP11470，CF960H。

1.6 线段树二分

线段树的分治结构帮助我们将二分和查询的过程合并在一起做到 $O (\log n)$ 。

1.6.1 全局查询

考虑这样一个问题：单点修改，全局查询前缀和大于 $S$ 的第一个位置 $p$ 。序列中每个元素非负，答案满足可二分性。若直接二分，每次查询单点前缀和，时间复杂度 $O (q \log^{2} n)$ 。

考察二分过程，第一次查询 $[1, n]$ 中点 $m$ 处的前缀和 $s_{m}$ ，它等于线段树根结点左儿子的权值。若 $s_{m} > S$ ，说明答案在 $[1, m]$ ，否则答案在 $[m + 1, n]$ 。对于前者，第二次查询 $[1, m]$ 中点 $m_{2}$ 处的前缀和 $s_{m_{2}}$ ，它等于根结点左儿子的左儿子的权值；对于后者，第二次查询 $[m + 1, r]$ 中点 $m_{2}^{'}$ 处的前缀和，它等于 $s_{m}$ 加上根结点右儿子的左儿子的权值。

我们发现，在不断递归的过程中，每次向右走，都需要将左儿子的权值累计入前缀和 $c u r$ ；而每次查询当前区间中点的前缀和，都相当于将累计的前缀和 $c u r$ 与左儿子权值相加。进入叶子结点时，就说明找到了答案。

当前二分区间就是当前结点对应的区间，在线段树上从根往叶子走的过程就是不断缩小二分区间的过程。

1.6.2 区间查询

尝试将 $[l, r]$ 的询问转化为原问题。注意前缀和从 $l$ 开始。

考虑 $[l, r]$ 在线段树上的拆分区间 $[l_{i}, r_{i}]$ （ $1 \leq i \leq k$ ），其中 $l_{1} = l$ ， $r_{i} + 1 = l_{i + 1}$ （ $1 \leq i < k$ ）， $r_{k} = r$ 。从小到大枚举 $i$ ，并记录 $[l_{1}, r_{i}]$ 的和 $S_{i}$ 。当 $S_{i}$ 第一次大于 $S$ 时，说明答案落在 $[l_{i}, r_{i}]$ 内，将 $S_{i - 1}$ 当成当前累计的前缀和，在 $[l_{i}, r_{i}]$ 的子树内二分即可。

先找拆分区间再二分太麻烦了，考虑将这两个步骤结合在一起，即先按 $i$ 从小到大的顺序访问拆分区间 $[l_{i}, r_{i}]$ ，再在包含答案的区间内二分。这导致答案并不一定在当前区间，所以需要返回 $- 1$ 表示答案不在当前区间。

设查询区间为 $q l, q r$ ，当前区间为 $l, r$ 。

若当前区间包含于查询区间（子树内二分），即 $[l, r] \subseteq [q l, q r]$ ：
- 若 $c u r$ 加上当前区间的值不大于 $S$ ，说明答案不在当前区间内，也说明答案大于 $r$ 。我们令 $c u r$ 加上当前区间的值，然后返回 $- 1$ 。
- 否则，若 $l = r$ ，返回 $l$ 表示答案。
- 否则，先递归左儿子 $[l, m]$ ，若返回值不为 $- 1$ ，则返回答案。
- 否则，返回 $[m + 1, r]$ 的返回值。
否则（寻找拆分区间），若 $[l, m]$ 和 $[q l, q r]$ 有交，则查询 $[l, m]$ 。若返回值不为 $- 1$ ，说明答案在左子区间的拆分区间内，返回答案。
否则，若 $[m + 1, r]$ 和 $[q l, q r]$ 有交，则查询 $[m + 1, r]$ 。若返回值不为 $- 1$ ，说明答案在右子区间的拆分区间内，返回答案。
否则，答案不在当前区间内，返回 $- 1$ 。

上述做法可以判断无解。

1.6.3 具体实现

在第三步中，没有必要判断返回值是否为 $- 1$ 。无论是否进入第四步，都是返回右子区间的答案。

此外，第二、三步和第一步的第三、四小步的形式相同，没有必要写两遍。

经过简化，可以写出如下代码：

int binary(int l, int r, int ql, int qr, int x, int &cur, int lim) {
  if(ql <= l && r <= qr) {
    if(cur + val[x] <= lim) return cur += val[x], -1; // 目标位置不在当前区间，返回
    if(l == r) return l; // 目标位置在当前区间且长度为 1，找到目标位置
    // 否则继续二分
  }
  int m = l + r >> 1;
  if(ql <= m) {
    int res = binary(l, m, ql, qr, x << 1, cur, lim);
    if(res != -1) return res;
  }
  if(m < qr) return binary(m + 1, r, ql, qr, x << 1 | 1, cur, lim);
  return -1;
}

实际上，如果查询信息单调且和左端点无关（信息和查询的左端点无关，如全局前缀和），代码还可以简化为：

int binary(int l, int r, int ql, int qr, int x, int lim) {
  if(val[x] <= lim) return -1; // 目标位置不在当前区间
  if(l == r) return l;
  int m = l + r >> 1;
  if(ql <= m) {
    int res = binary(l, m, ql, qr, x << 1, lim);
    if(res != -1) return res;
  }
  if(m < qr) return binary(m + 1, r, ql, qr, x << 1 | 1, lim);
  return -1;
}

例题：CF241B，CF407E，CF773E，CF765F，CF671E。

1.7 例题

SP11470 TTM - To the moon

可持久化线段树 + 标记永久化板子题。

时空复杂度 $O (n + q \log n)$ 。代码。

CF960H Santa's Gift

将贡献式展开，得到 $\frac{b_{x}^{2} \sum S_{i}^{2} - 2 b_{x} C \sum S_{i}}{n} + C^{2}$ 。对每个颜色维护每个点的子树内含有该颜色的结点个数的和与平方和。因为只有单点修改颜色，对应修改一条链上所有点关于某个颜色的 $S_{i}$ ，树剖 + 动态开点线段树维护，注意 push_down 时新开结点，或者使用标记永久化。

时空复杂度 $O ((n + q) \log^{2} n)$ ，代码。

CF241B Friends

异或粽子的加强版，复杂度稍劣。

考虑二分求出第 $k$ 大异或和 $v$ ，再求出不小于 $v$ 的异或和之和。

建出所有 $a_{i}$ 形成的 01 Trie，快速求出 $a_{i} \oplus a_{j} \geq v$ 的 $a_{j}$ 的数量。这部分复杂度是 $O (n \log^{2} v)$ 。

将二分和 01 Trie 结合起来可做到 $O (n \log v)$ ：递归时考虑所有 $a_{i}$ 对应贡献即可。

异或和之和较难处理，考虑统计每一位的答案。维护子树内每一位为 $1$ 的元素数量即可。

时空复杂度 $O (n \log^{2} v)$ 。代码。

将 $a_{i}$ 排序后每个子树内的元素是一段区间，对 $a_{i}$ 维护每一位为 $1$ 的元素数量关于下标的前缀和即可做到空间复杂度 $O (n \log v)$ 。

CF407E k-d-sequence

注意到区间合法当且仅当 $max a - min a \leq (r - l + k) d$ 且 $[l, r]$ 不含相同的数且 $[l, r]$ 模 $d$ 均相同。

将判断式变形为 $max a - min a + l d \leq (r + k) d$ 。

从左往右扫描线 $p$ ，维护 $[1, p]$ 每个点作为左端点， $p$ 作为右端点的判不等号左侧的值。单调栈 + 线段树区间修改。线段树二分查 $[L, p]$ 最小的，值不大于 $(p + k) d$ 的位置，其中 $L$ 表示第一个使得 $[L, p]$ 没有相同元素且模 $d$ 相同的位置。

时间复杂度 $O (n \log n)$ ，注意特判 $d = 0$ 的情况，且 $a_{i}$ 可以为负数。代码。

CF773E Blog Post Rating

首先可以证明 $a$ 单调不降一定是最优的，交换任意逆序对答案总不劣，分类讨论即可，具体细节略去。

根据 $a$ 的单调性，我们考虑当前帖子的评级，它一定是先单调减，再单调不降。如果我们知道了拐点 $p$ ，也就是评级的最低点，那么在 $p$ 之后的 $a_{i}$ 的贡献形如 “最终值不会超过 $a_{i} + (k - i)$ ”，拆成 $k + min (a_{i} - i)$ 可权值线段树维护。因为 $a_{i}$ 表示值， $i$ 表示排名，所以线段树上每个叶子维护 $v_{i}$ 表示 $i - c_{i}$ ，其中 $c_{i}$ 表示 $\leq i$ 的值的个数，非叶子维护 $v_{i}$ 区间最小值。修改形如从 $a_{i}$ 开始的后缀 $- 1$ ，打懒标记即可，查询时查从 $p$ 开始的后缀最小值。

问题变成了求解拐点 $p$ 。可知若 $- c_{i} \leq i$ ，则拐点一定在 $i$ 或 $i$ 之前，因为 $i$ 之后不会再减小了。如果在 $j > i$ 处继续减小，那么评级从 $- c_{i}$ 变成 $- c_{i} - 1$ ，必须满足 $j < - c_{i}$ ，这与 $- c_{i} \leq i < j$ 矛盾。因此，二分出第一个 $- c_{p} \leq p$ 的位置 $p$ ，则 $p$ 为拐点。

线段树二分实现上述过程，时间复杂度 $O (n \log n)$ 。代码。

P8868 [NOIP2022] 比赛

设 $T_{i, j}$ 表示 $q = i$ 且 $p = j$ 时的答案。对 $T_{i}$ ，设 $c_{j} = {max}_{k = j}^{i} a_{k}$ ， $d_{j} = {max}_{k = j}^{i} b_{k}$ ，则 $T_{i, j} = c_{j} d_{j}$ 。

扫描线，考虑 $T_{i - 1} \to T_{i}$ 。加入 $a_{i}$ 时，考虑它对 $c_{j}$ 的影响，相当于若干段区间加法。由单调栈可知整个过程的总段数为 $O (n)$ 。加入 $b_{i}$ 同理。因此用线段树维护 $T_{i}$ 。

询问 $[l, r]$ 的答案相当于对所有 $T_{i} (l \leq i \leq r)$ 的 $[l, i]$ 区间和求和。改变求和顺序，相当于对所有 $j \in [l, r]$ ，查询 $T_{i, j} (j \leq i \leq r)$ 之和。因为 $i < j$ 时 $T_{i, j} = 0$ ，所以又可以写成 $T_{i, j} (i \leq r)$ 之和，即 $T_{r}$ 上 $[l, r]$ 的区间历史和。

问题转化为 $c_{i}, d_{i}$ 区间加，查询区间 $\sum c_{i} d_{i}$ 历史和。

对于懒标记，维护 $(d c, d d, t, h c, h d, h c d)$ 分别表示 $Δ c$ ， $Δ d$ ，求和轮数，每轮求和的 $d c$ 之和即 $d c$ 历史和， $d d$ 历史和，以及 $d c \cdot d d$ 历史和。
对于信息，维护 $(n u m, s c, s d, s c d, h c d)$ 分别表示区间长度，区间 $\sum c$ ，区间 $\sum d$ ，区间 $\sum c d$ 和区间 $\sum c d$ 历史和。

时间复杂度 $O ((n + q) \log n)$ ，空间复杂度线性。代码。

*CF765F Souvenirs

首先规定 $(i, j)$ 的形态。因为 $(i, j)$ 和 $(j, i)$ 等价，所以不妨设 $i < j$ 。在此基础上，不妨设 $a_{i} \geq a_{j}$ 。对于 $a_{i} < a_{j}$ 的情况，可取反后再做一遍。

按 $j$ 扫描线对每个 $i$ 维护询问 $[i, j]$ 的答案 $f_{i}$ ，则扫到 $j$ 时每个 $i < j$ 且 $a_{i} \geq a_{j}$ 会对 $k \leq i$ 产生 $a_{i} - a_{j}$ 的贡献。 $i$ 向左跳动时， $a_{i}$ 只有减小才可能更新答案。因此直接查询所有 $\geq a_{j}$ 且小于当前 $a_{i}$ 的 $i$ 左边的第一个数 $a_{i^{'}}$ ，则 $i$ 跳动至 $i^{'}$ 。对 $i^{'}$ 的查询可以按 $a_{j}$ 从大到小建可持久化线段树，维护区间最小值，然后在 $a_{j}$ 对应线段树上二分即可。

但这样复杂度依然无法承受。进一步考察性质，我们发现，如果 $(i^{'}, j)$ 可能贡献至答案，则因为包含 $[i^{'}, j]$ 的区间必然包含 $[i^{'}, i]$ 和 $[i, j]$ ，所以 $a_{i^{'}} - a_{j}$ 必然小于 $a_{i} - a_{j}$ 的一半，否则 $a_{i} - a_{i^{'}}$ 一定比 $a_{i^{'}} - a_{j}$ 优。这样我们就可以将跳动 $i$ 的次数将至 $O (\log V)$ 。

进一步离线 $i^{'}$ 的查询可以将可持久化线段树转化为普通线段树。而对 $f$ 进行的前缀取 $min$ 单点求值可直接 BIT 维护。

时间复杂度 $O ((n \log n + q) \log V)$ 。代码。

*CF671E Organizing a Race

设 $a_{i} = a_{i - 1} + w_{i - 1} - g_{i - 1}$ 且 $a_{1} = 0$ ，则 $a_{j} - a_{i}$ （ $i < j$ ）表示从 $i$ 到 $j$ 且不吃 $j$ 的加油站时，需要消耗多少油量。

设 $b_{i} = b_{i + 1} + w_{i} - g_{i + 1}$ 且 $b_{n} = 0$ ，则 $b_{i} - b_{j}$ （ $i < j$ ）表示从 $j$ 到 $i$ 且不吃 $i$ 的加油站时，需要消耗多少油量。

那么 $k = 0$ 时 $[l, r]$ 合法当且仅当 $a_{l} \geq {max}_{p = l}^{r} a_{p}$ 且 $b_{r} \geq {max}_{p = l}^{r} b_{p}$ 。

给 $g_{i}$ 加 $1$ 产生的影响为将 $a_{i + 1 \sim n}$ 减去 $1$ ，将 $b_{1 \sim i - 1}$ 减去 $1$ 。因为只比较相对大小，所以也可以理解为将 $a_{1 \sim i}$ 加上 $1$ ，将 $b_{i \sim n}$ 加上 $1$ 。

考虑从左往右开，发现当遇到 $a_{i} > a_{l}$ 时，需要在 $l \sim i - 1$ 的位置进行 $a_{i} - a_{l}$ 次操作，之后 $a_{l}$ 变成 $a_{i}$ ，可以继续开。考虑到还要从右往左走，一定是操作 $i - 1$ 最优。反证 + 调整易证。

设 $s u c_{i}$ 表示最小的 $j > i$ 使得 $a_{j} > a_{i}$ ，那么从 $l$ 出发相当于操作 $a_{s u c_{i}} - a_{i}$ 次 $s u c_{i} - 1$ ，操作 $a_{s u c_{s u c_{i}}} - a_{s u c_{i}}$ 次 $s u c_{s u c_{i}} - 1$ ，以此类推。从右往左扫描线，用单调栈 + 线段树维护从 $l$ 出发进行所有这样的操作之后现在的 $b$ ，记作 $b^{'}$ 。

求出 $l i m$ 表示最小的 $j > i$ 使得 $a_{j} > a_{i} + k$ ，那么 $r \geq l i m$ 不合法。

对于剩余操作，直接加在 $g_{r}$ 上最优。因此，问题转化为求最大的 $r < l i m$ ，使得 $b_{r} + k \geq {max}_{i = l}^{r} b_{i}^{'}$ 。显然 $r$ 一定在单调栈上，即若 $r_{1} < r_{2}$ 且 $b_{r_{1}} > b_{r_{2}}$ ，那么 $r_{2}$ 没用。但是我们不能二分，因为 $r$ 合法不代表 $r^{'} < r$ 也合法，即使是在单调栈上。枚举也不行。

但令人惊讶的是，我们可以检查一段区间 $[p, q]$ 内是否有合法的 $r$ 。找到区间最大的 $b_{i}$ 。因为 $b_{i}$ 最大，而 $b_{j}^{'}$ 由 $b_{j}$ 加上一个不大于 $k$ 的值得到，所以 $b_{p \sim i}^{'} \leq b_{i} + k$ 。如果 $b_{i}$ 不合法，那么 ${max}_{j = 1}^{p - 1} b_{j}^{'} > b_{i} + k$ ，显然整个区间也不合法。

于是我们又可以二分了。每次二分需要查询 $b$ 和 $b^{'}$ 的区间 $max$ ，前者 ST 表，后者线段树。时间复杂度 $O (n \log^{2} n)$ 。

不妨认为 $b_{1 \sim l - 1} = - \infty$ ，直接在线段树上二分即可做到 $O (n \log n)$ 。向右递归时，将当前维护的 ${max}_{j = 1}^{p - 1} b_{j}^{'}$ 和左子树的值取 $max$ 。代码。

2. 可持久化线段树

前置知识：动态开点线段树。

可持久化线段树在 NOI 大纲里是 8 级算法，也称主席树。它用于描述平面上的可减信息，支持矩形查询，常见于强制在线的二维数点问题。

2.1 算法简介

对一棵线段树 $T_{0}$ 进行 $q$ 次单点修改，依次得到 $T_{1}, T_{2}, \dots, T_{q}$ 。如果我们要得到每棵线段树的信息，朴素地存储是不可接受的。

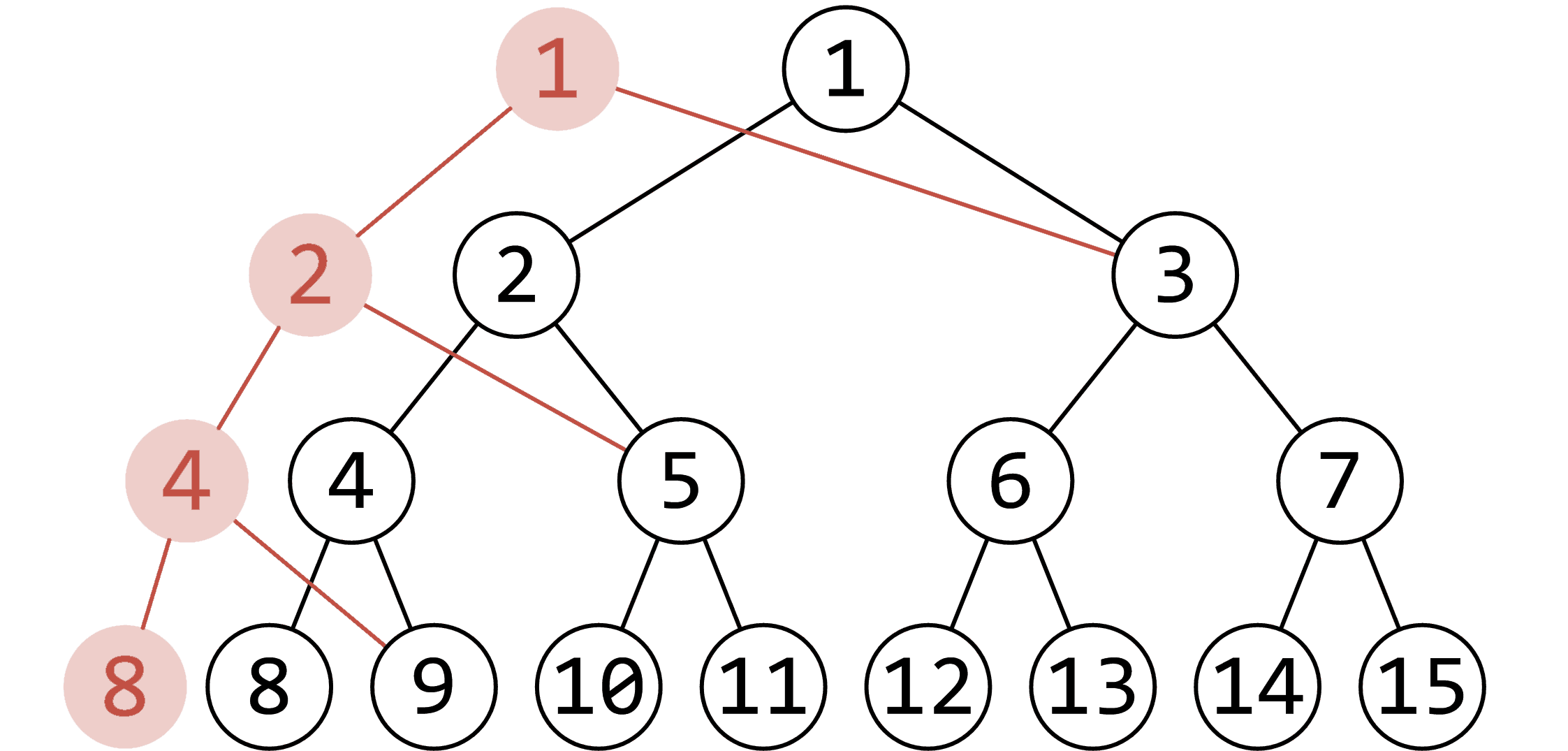
注意到单次修改只会改变 $O (\log n)$ 个线段树结点的信息。对于这些更新，我们新开结点存储，另一侧儿子继承原来的结点，就可以保证原线段树信息不被破坏。如下图，红色结点为新建结点，数字为对应原线段树标号（不是真实标号）。图源 OI-Wiki。

以下是维护单点修改，区间求和的线段树的可持久化版本的修改部分。

void modify(int pre, int &x, int l, int r, int p, int v) {
  val[x = ++node] = val[pre];
  ls[x] = ls[pre], rs[x] = rs[pre]; // 继承原来的结点.
  if(l == r) return val[x] = v, void();
  int m = l + r >> 1;
  if(p <= m) modify(ls[pre], ls[x], l, m, p, v);
  else modify(rs[pre], rs[x], m + 1, r, p, v);
  val[x] = val[ls[x]] + val[rs[x]];
}

若可持久化线段树涉及区间修改，下传懒标记时必须新建结点，空间常数非常大。若修改性质较好，可以选择标记永久化而不下传懒标记。

2.2 应用

可持久化线段树刻画了 只含 $O (n)$ 可减信息的平面。普通线段树维护的是序列，是一维的信息。当信息可减时，我们对二维信息的其中一个维度扫描线，用线段树维护另一个维度的信息，并将整个过程可持久化，就可以查询平面信息。

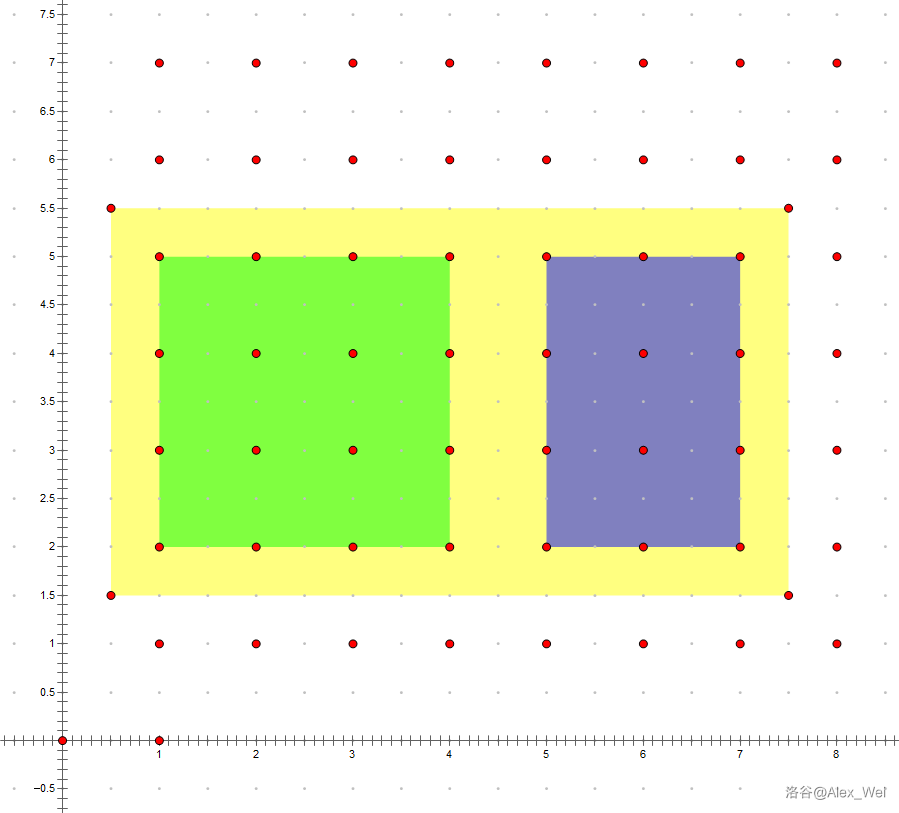
例如，平面上有若干点，每个点有权值，多次查询一个矩形范围内所有点的权值之和。对横坐标扫描线，用可持久化线段树维护每个纵坐标的点权关于横坐标的前缀和，即下标为 $y$ 的位置上是所有纵坐标为 $y$ 且横坐标不超过当前横坐标的点权和。查询时，用横坐标较大值的纵坐标区间点权和（黄色部分），减去横坐标较小值 $- 1$ 的纵坐标区间点权和（绿色部分），就是矩形点权和（蓝色部分）。

如果不强制在线，则可以将询问离线，拆成两个对应横坐标的询问，一次扫描线解决。当问题强制在线时，我们需要保存扫描到每个横坐标时线段树的形态，必须可持久化。一般地，对于二维数点问题，线段树和可持久化线段树之间差一个强制在线。

再例如区间第 $k$ 小值。每个元素有两个信息：下标和权值。在权值线段树上二分可以求出构成该权值线段树的所有元素的第 $k$ 小值。在 $a_{i \sim j}$ 构成的权值线段树上二分，也就是 $a_{1 \sim j}$ 的权值线段树减去 $a_{1 \sim i - 1}$ 的权值线段树，就可以查询区间 $[i, j]$ 的第 $k$ 小值。因此，对序列下标扫描线，用可持久化权值线段树维护每个值在当前前缀的出现次数即可。

此外，可持久化线段树还可以维护扫描线的过程中，每个时刻的线段树形态。这样的问题一般可以抽象成以下形式：有 $n$ 个事件，每个事件产生作用的时间范围是 $[l_{i}, r_{i}]$ 。我们对时间扫描线，用可持久化线段树维护包含当前时刻的事件产生的影响，即得每个时刻的完整信息。例题如 P3168。

2.3 扩展

可持久化线段树维护静态平面信息。动态维护平面需要树套树。

可持久化线段树扩展到树上：每个结点继承并修改其父亲的线段树，序列前缀和变成树上前缀和。

2.3.1 可持久化数组

我们知道，线段树可以维护序列。自然地，可持久化线段树可以维护可持久化序列，相当于将单点修改单点查询的线段树可持久化。

特别地，如果支持离线，则可以对版本之间的依赖关系建树，最后 DFS，用数据结构维护当前版本的答案（EI）。

2.3.2 可持久化树状结构

容易将可持久化线段树的思想扩展到其它树形数据结构上，如 01-Trie，李超线段树，平衡树等。

可持久化 01-Trie 支持查询某个值和一段区间内所有数的异或最大值（也可以查询第 $k$ 大异或值）。按位贪心，做法和区间第 $k$ 大类似。

可持久化平衡树将在平衡树文章中专门介绍。

2.3.3 可持久化并查集

合并两个元素时，修改其中一个代表元指向的父结点，用可持久化数组维护。注意不能使用基于均摊的路径压缩，必须按秩合并，所以既要维护 $f a$ ，也要维护大小或深度。单次查询代表元需 $O (\log n)$ 次查询数组某一位的值，所以复杂度为 $O (n \log^{2} n)$ 。

可持久化并查集可以维护边权有大小限制（不能两端都有限制）时，所有合法的边形成的连通块形态。按边权从小到大的顺序将每条边加入并查集，每加入一条边就记录一个版本的 $f a$ 。给出 $(u, v, w)$ ，询问能否不经过权值不大于 $w$ 的边从 $u$ 走到 $v$ ，就是在加入边权最大且不大于 $w$ 的边之后的那个版本的并查集中查询 $u, v$ 代表元是否相同。此时可持久化并查集可以被 Kruskal 重构树以更优的复杂度代替。Kurskal 重构树见树论。

2.4 例题

P3834【模板】可持久化线段树 2

区间第 $k$ 大，可持久化线段树的经典应用。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e5 + 5;
constexpr int K = N << 5;
int n, m, a[N], b[N];
int node, R[N], ls[K], rs[K], val[K];
void modify(int pre, int &x, int l, int r, int p) {
  val[x = ++node] = val[pre] + 1;
  ls[x] = ls[pre], rs[x] = rs[pre];
  if(l == r) return;
  int m = l + r >> 1;
  if(p <= m) modify(ls[pre], ls[x], l, m, p);
  else modify(rs[pre], rs[x], m + 1, r, p);
}
int query(int l, int r, int x, int y, int k) {
  if(l == r) return b[l];
  int m = l + r >> 1, v = val[ls[y]] - val[ls[x]];
  if(k <= v) return query(l, m, ls[x], ls[y], k);
  return query(m + 1, r, rs[x], rs[y], k - v);
}
int main() {
  cin >> n >> m;
  for(int i = 1; i <= n; i++) cin >> a[i], b[i] = a[i];
  sort(b + 1, b + n + 1);
  for(int i = 1; i <= n; i++) a[i] = lower_bound(b + 1, b + n + 1, a[i]) - b;
  for(int i = 1; i <= n; i++) modify(R[i - 1], R[i], 1, n, a[i]);
  for(int i = 1; i <= m; i++) {
    int l, r, k;
    cin >> l >> r >> k;
    cout << query(1, n, R[l - 1], R[r], k) << "\n";
  }
  return 0;
}

P4735 最大异或和

可持久化 01-Trie 模板题。注意一开始要加入一个 $0$ 。

时间复杂度 $O (n \log v)$ 。代码。

P3402 可持久化并查集

启发式合并，用可持久化数组维护 $f a$ 和 $s z$ 两个数组的各个版本。

时间复杂度 $O (m \log^{2} n)$ 。代码。

P4592 [TJOI2018] 异或

对于询问 1，在树上可持久化 01-Trie 上二分。对于询问 2，用 DFS 序拍平后相当于区间询问与给定值的最大异或和，序列可持久化 01-Trie 即可。

时间复杂度 $O ((n + q) \log n)$ ，代码。

P3168 [CQOI2015] 任务查询系统

对时间扫描线，维护每个时间的以优先级为下标的权值线段树，记录每个优先级有多少个任务，就是主席树板子了。注意查询时叶子结点产生贡献的任务数量要和 $k$ 取 $min$ （易错）。

时间复杂度线性对数。代码。

P2633 Count on a tree

树上可持久化线段树板子题。

代码。

P4137 Rmq Problem / mex

设 $f_{i, j}$ 表示 $j$ 在 $\leq i$ 的位置中，最后一次出现的位置。 $[l, r]$ 的区间 $mex$ 相当于最小的 $v$ 使得 $f_{i, v} < l$ 。

主席树维护 $f$ 或离线扫描线均可。

时间复杂度 $O ((n + m) \log n)$ 。代码。

P3293 [SCOI2016] 美味

从高位往低位贪心。设已经选择的所有位的数字为 $d$ ，若 $b$ 的当前位为 $0$ ，则检查 $a_{l \sim r}$ 是否存在值落在 $[d + 2^{i} - x, d + 2^{i + 1} - x)$ 的数，反之检查是否存在值落在 $[d - x, d + 2^{i} - x)$ 的数。在线二维数点（需要立刻知道结果才能进一步贪心），可持久化线段树即可。

时间复杂度 $O ((m \log V + n) \log V)$ 。代码。

CF840D Destiny

如果一个数出现了不小于 $k$ 次，那么从小到大排序后它一定占据了长度不小于 $k$ 的区间。排序后每 $k$ 个位置取出一个数检查是否符合条件，必然能取出所有符合条件的数。

主席树维护区间第 $k$ 大，求区间内某个数的出现次数。

时间复杂度 $O (n k \log n)$ 。代码。

P2048 [NOI2010] 超级钢琴

做一遍前缀和。

用优先队列维护每个左端点对应权值最大的右端点产生的贡献。每次取出权值最大的左端点，然后计算该左端点对应权值次大的右端点产生的贡献，加入优先队列，以此类推。取出 $k$ 次权值之和即为答案。

静态区间第 $k$ 大，可持久化线段树即可。

时间复杂度 $O ((n + k) \log n)$ 代码。

双倍经验：异或粽子。

P4559 [JSOI2018] 列队

考虑一次询问，设学生的位置分别为 $x_{0} < x_{1} < \dots < x_{k}$ （ $k = r - l$ ），手动模拟发现存在分界点 $p$ ，使得 $x_{p}$ 及其左边的学生向右跑， $x_{p}$ 右边的学生向左跑。考察 $x_{i}$ 和 $i$ 的最终位置 $K + i$ ，两式相减得 $F (i) = x_{i} - (K + i)$ ，则 $i$ 产生的贡献即 $| F (i) |$ 。

因为 $x_{i}$ 互不相同，所以 $x_{i}$ 相较于 $x_{i - 1}$ 增加不小于 $1$ ，而 $K + i$ 相较于 $K + i - 1$ 恰好增加 $1$ ，因此 $F (i) - F (i - 1) = x_{i} - x_{i - 1} - 1 \geq 0$ ，即 $F (i)$ 单调不降，因此存在 $p$ 使得 $F (p) \leq 0$ 且 $F (p + 1) > 0$ ，这样 $p$ 左边的学生就要向右跑，右边的学生向左跑。

线段树二分找到 $p$ ，求出 $p$ 左边的学生个数与位置之和， $p$ 右边的学生个数与位置之和，从而计算答案。

对于多组询问，套可持久化线段树即可。

时间复杂度 $O ((n + m) \log n)$ 。代码。

P4098 [HEOI2013] ALO

对于每个 非最大值 元素 $a_{i}$ ，考虑求出其两侧第二个大于 $a_{i}$ 的位置 $l_{i}, r_{i}$ ，则 $[l_{i} + 1, r_{i} - 1]$ 和 $a_{i}$ 均产生贡献： $[l_{i} + 1, i]$ 和 $[i, r_{i} - 1]$ 的次大值均为 $a_{i}$ 。特别地，若 $l_{i}$ 不存在则为 $0$ ，因为 $a_{i}$ 不是最大值，所以总存在 $[1, x]$ 使得 $a_{i}$ 为次大值。同理，若 $r_{i}$ 不存在则为 $n + 1$ 。求 $a_{i}$ 和一段区间内所有数异或值最大值用可持久化 01-Trie 即可。

$l_{i}$ 和 $r_{i}$ 的求法：排序后用双向链表维护当前剩余的位置，或者用单调栈：不妨设要求 $l_{i}$ ，先求大于当前元素的前驱位置，然后将所有位置按照前驱位置为第一关键字，元素值为第二关键字排序，扫描过程中将前一个位置的前驱到当前位置的前驱的前一个元素加入单调栈，然后用当前位置的值更新单调栈（即弹出小于当前元素的栈顶，但不加入当前元素），则栈顶位置即 $l_{i}$ 。读者可自行思考其正确性（证明思路：前驱元素大于当前元素）。

时间复杂度 $O (n \log V)$ 。代码。

*P2839 [国家集训队] middle

要求中位数恰好等于某个值是困难的，但 要求中位数不小于某个值是容易的。检查中位数是否不小于 $x$ ，使用经典套路转化为：小于 $x$ 的数视作 $- 1$ ，不小于 $x$ 的数视作 $1$ ，根据题目的中位数定义，要求区间和非负。

因此，我们二分答案，检查 “答案是否不小于 $x$ ”：求对于转化后的序列，端点分别在 $[a, b]$ ， $[c, d]$ 的区间之和的最大值是否不小于 $0$ 。进一步转化为 $[a, b)$ 的最大可空后缀和，加上 $[b, c]$ 的和，再加上 $(c, d]$ 的最大可空前缀和，线段树维护。

但是我们不能对每个二分值都建线段树。注意到每个数在二分值不小于它的线段树上是 $1$ ，在二分值大于它的线段树上是 $- 1$ 。如果按权值从小到大添加数，每个数只会改变一次。强制在线，可持久化线段树即可。

时间复杂度 $O (n \log n + q \log^{2} n)$ 。代码。

P7518 [省选联考 2021 A/B 卷] 宝石

宝石一定是能吃就吃，先吃一定不比后吃劣（调整法易证）。

设 $d = lca (s, t)$ ，将路径分成 $s \to d$ 和 $d \to t$ 两段。

对于 $s \to d$ ，找到 $s$ 的第一个出售 $P_{1}$ 的祖先 $x_{1}$ ，然后找到 $x_{1}$ 的第一个出售 $P_{2}$ 的祖先 $x_{2}$ ，以此类推，直到祖先深度小于 $d$ 。记录已经收取的宝石数量 $c$ 。

注意到对于每个 $x_{i}$ ，对应的 $x_{i + 1}$ 是固定的，等于在 $x_{i}$ 处收集宝石后，下一个可以收集宝石的祖先。即考虑 $w_{x_{i}}$ 在宝石序列中的后继，第一个出售该后继宝石的祖先。

对于 $d \to t$ ，二分答案 $m i d$ ，找到 $t$ 的第一个出售 $P_{m i d}$ 的祖先 $x$ 。类似地，预处理 $g_{i}$ 表示考虑 $w_{i}$ 在宝石序列中的前驱，第一个出售该前驱宝石的祖先，则相当于检查从 $x$ 开始跳 $m i d - c - 1$ 次 $g$ ，最终跳到的结点是否仍在路径上，即深度不小于 $d$ 。

倍增优化跳 $f, g$ 的过程，用树上可持久化线段树维护每个结点最近的出售每个宝石的祖先。

时间复杂度线性对数平方。代码。

P6071 『MdOI R1』Treequery

若 $l \leq p \leq r$ ，答案为 $0$ 。

任选结点为根，设 $l \sim r$ 的 LCA 为 $d$ ：

若 $l \sim r$ 全部在子树内，则答案为 $dis (p, d)$ 。
若 $l \sim r$ 全部在子树外：
- 若 $p$ 不在 $d$ 子树内，则答案为 $dis (p, d)$ 。
- 否则，答案为 $dis (p, d^{'})$ ，其中 $d^{'}$ 表示 $p$ 的最近的子树内有 $l \sim r$ 某点的祖先，则 $d^{'}$ 一定有 $l \sim r$ 中 $p$ 关于时间戳的前驱或后继。
否则答案为 $0$ 。

用主席树支持上述查询。

时间复杂度 $O ((n + m) \log n)$ 。代码。

CF464E The Classic Problem

值域过大，考虑用线段树维护从 $s$ 到每个点的最短距离的二进制。

给第 $w$ 位加一首先需要线段树上二分找到距离它最近的零位 $p$ （ $w \leq p$ ），将 $[w, p)$ 清零，第 $p$ 位改成 $1$ 。比较两棵线段树时，从高到低 二分找到第一个不同的位并比较，通过记录哈希值判相等。

使用可持久化线段树存每个点的 $d i s t$ 跑 Dijkstra。

时间复杂度 $O (m \log m \log x)$ 。代码。

*CF453E Little Pony and Lord Tirek

区间覆盖考虑珂朵莉树（set 维护连续段），对于每个询问，找出其覆盖的所有时间连续段 $(l_{i}, r_{i}, t_{i})$ ，相当于查询 $l_{i} \sim r_{i}$ 的位置经过 $t - t_{i}$ 时刻后的值之和。对于 $\frac{m_{p}}{r_{p}} < t - t_{i}$ 的 $p$ 查询 $\sum m_{p}$ ，对 $\frac{m_{p}}{r_{p}} \geq t - t_{i}$ 的 $p$ 查询 $t \sum r_{p}$ 。

二维数点，可持久化线段树即可。

时间复杂度 $O ((n + m) \log n)$ 。代码。

3. 线段树合并

前置知识：动态开点线段树。

线段树合并常见于树上问题，合并若干儿子子树的线段树得到当前点的线段树。它可以和多种算法相结合，有很大的应用空间，例如维护 SAM 的 endpos 集合，优化树形 DP。

相比而言，线段树分裂的用处不多。它可以和 set 维护连续段（ODT）的技巧一起使用，支持区间排序。

3.1 算法介绍

合并两棵 下标范围相同 的线段树，分别记为 $T_{x}$ 和 $T_{y}$ 。

因为一棵树与空结点合并的结果为它本身，所以若两棵树的当前区间 $x, y$ 至少有一个为空则返回。否则，新建结点（原因在本小节最后） $z$ 表示 $T_{x}, T_{y}$ 合并后的线段树 $T_{z}$ 当前区间的对应结点， $z$ 的左子树即 $x$ 的左子树和 $y$ 的左子树合并得到的结果，右子树同理。

综上，得以下步骤：从 $T_{x}$ 和 $T_{y}$ 的根 $R_{x}, R_{y}$ 开始递归。设当前区间在两棵树上对应结点分别为 $x, y$ 。

若 $x, y$ 至少有一个为空，则返回另一个。
否则新建结点 $z$ ，继续递归当前区间的左子区间和右子区间。令 $z$ 的左儿子为 $x$ 的左儿子和 $y$ 的左儿子合并的结果，右儿子同理。合并 $z$ 的左右儿子的信息，并返回 $z$ 。
递归到叶子时直接合并。这是容易的，因为只涉及两个长度为 $1$ 的区间的信息。但注意：合并叶子与合并左右儿子可能是不同种类的合并操作。例如叶子相加，左右儿子取 $max$ 。

int merge(int l, int r, int x, int y) {
  if(!x || !y) return x | y;
  int m = l + r >> 1, z = ++node;
  if(l == r) return /* 合并叶子 x 和 y */, z;
  ls[z] = merge(l, m, ls[x], ls[y]);
  rs[z] = merge(m + 1, r, rs[x], rs[y]);
  return /* 合并左右儿子 */, z;
}

复杂度分析：每次合并的复杂度为两棵线段树重合的结点个数，也就是删去的结点个数。因此，线段树合并的总复杂度为所有线段树的结点个数之和。常见情况是初始有 $n$ 棵线段树，每棵线段树仅一个位置有值，合并这些线段树的时间、空间复杂度为 $O (n \log V)$ 。

笔者总结的注意点与技巧：

若线段树合并不新建结点，则整个过程会破坏原有线段树的结构。如果我们将 $y$ 的信息合并到 $x$ 上，则对于所有包含结点 $x$ 的线段树，其存储的信息均会改变。但我们希望只更新当前线段树在结点 $x$ 对应的下标区间的信息。这和 可持久化 数据结构新建结点的原因相同，也称可持久化线段树合并。打个比方，借了同学的笔记，就不应在上面乱涂乱画，将其他同学的笔记抄在上面，而是拿一本新笔记本，将这个同学和其他同学的笔记抄在上面，除非同学已经用不上他的笔记了（下一条）。
如果被合并的线段树 $T_{y}$ 的信息在合并后不会用到（询问离线后及时查询），那么可不新建结点而直接将 $y$ 的信息合并到 $x$ 上，即在上述步骤中用 $x$ 代替 $z$ ，从而有效减少空间开销。具体写法见 P3224。
merge 时尽量下传 $l, r$ ，因为需要判断是否递归到叶子，否则叶子将从两个空结点合并信息。若初始所有叶子至多在一棵线段树上出现，就可以不下传，因为递归到叶子时 $x, y$ 至少一个为空，直接返回了。当区间信息可快速合并且时也不需要下传，因为不从子结点合并东西上来，自然不用担心叶子合并两个空结点。一个满足前者的例子是线段树合并维护 SAM 的 endpos 集合。
易错点：如果使用可持久化线段树合并，且在所有子树合并完之后再加入当前点信息，则该步修改也要可持久化。
检查线段树合并是否适用，只需考察能否快速合并两个叶子以及快速 push_up，而不需要快速合并两个区间的信息。这是笔者在初学线段树合并时常犯的错误，即因无法快速合并两个有交区间的信息而认为无法线段树合并。注意这不同于 push_up，因为 push_up 合并的两个区间无交。
线段树合并的方式适用于 01-Trie 等其它本质上是动态开点线段树的结构的合并。

当线段树合并涉及区间修改时，情况就变得麻烦了。因为 线段树合并（叶子合并）的方式和信息与标记合并的方式不一定相同，所以需要具体问题具体分析，没有一般化的套路。例如区间加法，区间求和，但线段树合并时对应叶子取 $max$ 。尽管修改和询问性质很好，但仍无法维护。

此外，为了避免标记破坏线段树合并复杂度分析的条件，我们不能无条件地下传标记，否则将一直合并到叶子。解决方法有：

标记永久化。
称一个结点是空心的，当且仅当它的子树内只有它自己，即该结点是标记下传得到的结点，也即该结点维护的所有位置受到相同标记的作用。支持合并空心结点和普通结点，以及合并两个空心结点。这样空间常数较大，但时间、空间复杂度仍然正确。

3.2 应用

线段树合并描述了 从若干子结构合并成大结构的合并过程中所有出现过的结构的完整信息，所以它常用于实时维护连通块信息，或求出树上每个结点的子树信息。一个结点的子树信息等于该结点的信息合并其所有儿子的子树信息。

代替复杂度更高的 set 启发式合并。例如配合并查集实时维护连通块内所有结点。
求出后缀自动机的每个结点的 endpos 集合，因为一个结点的 endpos 集合等于它在 link 树上的子树内所有叶子的 endpos 集合的并。
求解深度相关的树上问题。如多次查询 $k$ 级儿子的信息，用线段树合并预处理出每个结点所有后代以深度作为下标的信息。这个例子也可以看成树上整体 DP。
其它树状数据结构也可以类似线段树一样合并，如 01-Trie。

此外，线段树合并还可以维护 树上整体 DP，即子结点向父结点转移的二维 DP，但大部分转移形如子结点对应位置进行运算，只有很少的特殊转移。一类经典问题是树上具有祖先后代关系的路径覆盖，对于下端在结点 $i$ 子树内的所有路径，我们只关心上端最浅深度 $j$ ，从而设计对应状态 $f_{i, j}$ 。转移时，用线段树合并维护所有儿子到当前结点的转移（通常为对应位置取最值），再考虑所有以当前结点为下端的路径产生的影响，通常为 $f_{i}$ 的单点修改或区间修改。

3.3 线段树分裂

和 FHQ Treap 分裂一样，线段树分裂有按值分裂和按排名分裂两种方法。

按排名分裂的流程如下：设当前区间为 $[l, r]$ ，对应结点 $x$ ，分裂出的线段树的当前区间对应结点为 新建结点 $y$ ，且保留 $T_{x}$ 维护的较小的 $k$ 个值。令 $v$ 为 $x$ 的左子树维护的值的个数，分三种情况讨论：

若 $k < v$ ，则将 $x$ 的右子树给 $y$ ，并向左子树分裂。
若 $k = v$ ，则将 $x$ 的右子树给 $y$ 后返回。这一步可以和上一步合并，单独拎出来判断可减小时间和空间常数。
若 $k > v$ ，则向右子树分裂，并令 $k$ 减去 $v$ 。

和线段树合并一样，线段树分裂需要特殊考虑叶子。使用一些技巧避免麻烦的判断。先看代码。

void split(int x, int &y, int k) {
  if(!x) return y = 0, void();
  y = ++node;
  if(k < val[ls[x]]) swap(rs[x], rs[y]), split(ls[x], ls[y], k);
  else if(k == val[ls[x]]) swap(rs[x], rs[y]);
  else split(rs[x], rs[y], k - val[ls[x]]);
  val[y] = val[x] - k, val[x] = k;
}

核心在第七行，我们不从子结点合并信息上来，而是直接通过原来的信息计算新的信息。当叶子出现 $c$ 次时，需要将其分裂成 $k$ 次和 $c - k$ 次，容易发现上述代码符合要求。

对于按值分裂，与上述过程类似。设需要保留 $T_{x}$ 小于等于 $k$ 的值，当前区间中点为 $m$ 。

若 $k \leq m$ ，则将 $x$ 的右子树给 $y$ ，并向左子树分裂。
若 $k > m$ ，则向右子树分裂。

特判若 $k = r$ 则返回，保证我们递归到叶子结点后返回。

void split(int l, int r, int x, int &y, int k) {
  if(!x || k == r) return y = 0, void();
  y = ++node;
  int m = l + r >> 1;
  if(k <= m) swap(rs[x], rs[y]), split(l, m, ls[x], ls[y], k);
  else split(m + 1, r, rs[x], rs[y], k);
  val[x] = val[ls[x]] + val[rs[x]];
  val[y] = val[ls[y]] + val[rs[y]];
}

一次分裂新建 $O (\log n)$ 个结点，时间、空间复杂度均为线性对数。线段树分裂可与线段树合并相结合，恰好保证了后者的复杂度。

3.4 例题

P3224 [HNOI2012] 永无乡

用线段树维护并查集每个连通块内部所有结点的信息。

时空复杂度线性对数。代码。

CF600E Lomsat gelral

以颜色编号为下标建线段树，维护区间出现次数最多的颜色编号和，线段树合并即可。代码。

其它板子题：Blood Cousins（查询 $p$ 级祖先有多少个 $p$ 级儿子，代码），Tree Requests（查询 $k$ 级儿子信息，代码）。

复杂度都是线性对数。

P4556 [Vani 有约会] 雨天的尾巴 /【模板】线段树合并

将链修改转化为树上差分，则一个房子的救济粮信息由差分后其子树所有信息之和得到，考虑线段树合并。注意每合并得到一个结点的真实信息就查询其答案，不然需要可持久化，空间开销过大。

时空复杂度线性对数。代码。

P5494 【模板】线段树分裂

对于操作 0，将 $[1, n]$ 分裂成 $[1, x - 1]$ ， $[x, y]$ 和 $[y + 1, n]$ ，再将 $[1, x - 1]$ 与 $[y + 1, n]$ 合并。

对于操作 1，将 $p, t$ 两棵线段树合并。

剩下都是权值线段树的基本操作。

时空复杂度线性对数。代码。

P2824 [HEOI2016/TJOI2016] 排序

使用 set 维护极长有序段，排序时对端点所在有序段进行分裂，再将所有覆盖到的有序段合并成一大段。通过线段树分裂与合并实现。

注意区间升序或降序会影响分裂时的细节，需要讨论。

时空复杂度 $O ((n + m) \log n)$ 。代码。

双倍经验：A Simple Task。

P3899 [湖南集训] 更为厉害

因为 $a, b$ 均为 $c$ 的祖先，所以 $a, b$ 互为祖先后代关系。

若 $b$ 为 $a$ 的祖先，则任何距离 $a$ 不超过 $k$ 的 $a$ 的祖先均可以成为 $b$ ，且任何 $a$ 子树内不等于 $a$ 的点均可以成为 $c$ ，因此贡献为 $min (d e p_{a} - 1, k) \times (s z_{a} - 1)$ ，其中 $d e p_{a}$ 表示深度， $s z_{a}$ 表示子树大小。

若 $a$ 为 $b$ 的祖先，则任何 $a$ 子树内不等于 $a$ 且距离 $a$ 不超过 $k$ 的结点均可以成为 $b$ ，对应的 $c$ 的方案数即 $s i z e_{b} - 1$ 。因此贡献为

\sum_{b \in subtree (a) \land dist (a, b) \leq k \land a \neq b} s z_{b} - 1

树上线段树合并维护每个结点 $u$ 的子树内每个深度的所有子结点的子树大小减去 $1$ 之和，询问时查 $a$ 对应的线段树上 $[d e p_{a} + 1, d e p_{a} + k]$ 的区间和。

注意合并时可持久化，或者离线回答询问。

时空复杂度线性对数。代码。

P6623 [省选联考 2020 A 卷] 树

将 01 Trie 倒过来建实现 01 Trie 全局加 1。套 01 Trie 合并即可。

时间复杂度 $O (n \log v)$ 。代码。

*P3521 [POI2011] ROT-Tree Rotations

对于每个结点，是否交换左右子树不影响它的祖先，可贪心确定。

用权值线段树维护子树内所有叶子权值的桶。合并时求出 $x$ 子树在 $y$ 子树前的逆序对数 $i n v$ ，则 $x$ 在 $y$ 后的逆序对数等于 $x$ 在 $y$ 前的顺序对数，即 $s z_{x} s z_{y} - i n v$ 。

在 $y$ 处统计逆序对时，我们需要知道 $T_{x}$ 权值大于当前区间右端点的叶子数。所以，优先递归右子树，并记录 $c n t$ 表示之。若 $y$ 为空，则令 $c n t$ 加上 $v a l_{x}$ ， $v a l_{x}$ 即 $x$ 对应区间包含的叶子数。若 $x$ 为空则在 $y$ 处统计答案，令逆序对个数加上 $v a l_{y} \times c n t$ ，因为每个 $y$ 的叶子和比它大的 $c n t$ 个 $T_{x}$ 的叶子均可形成逆序对。

本题不需要可持久化。因为每个结点的线段树合并完毕时，所需信息也已经统计完毕。

当前结点的答案等于左儿子和右儿子的答案相加，加上顺序对和逆序对数量的较小值。最终答案即根结点答案。

时空复杂度 $O (n \log n)$ 。代码和题解是反过来的。

P8907 [USACO22DEC] Making Friends P

答案等于总朋友关系数减去 $M$ 。

因为奶牛离开的顺序按编号从小到大，所以互相连边等价于编号最小的朋友向其它朋友连边。考虑到 $i$ 时，将编号最小的朋友 $j$ 的朋友集合对 $i$ 的朋友集合取并，再删去 $i$ 。线段树合并维护即可。

时间复杂度 $O (m \log n)$ 。代码。

CF490F Treeland Tour

整体 DP 经典题。 $n \leq 6000$ 太没劲了，直接做 $n \leq 10^{5}$ 。

先离散化。

随便选个点定根，考虑在每条路径的 LCA 处统计答案。为此，设 $f_{i, j}$ 表示从 $i$ 子树往 $i$ 方向的以 $j$ 结尾的最长上升子序列， $g_{i, j}$ 表示从 $i$ 往 $i$ 子树方向的以 $j$ 开头的最长上升子序列。

对于任意两个儿子 $u, v$ ，考虑它们的贡献：

若经过 $i$ ，则用 $1 + max f_{u, 1 \sim w_{i} - 1} + max g_{v, w_{i} + 1 \sim n}$ 更新答案。
若不经过 $i$ ，则对每个 $f_{u, j}$ ，用 $f_{u, j} + max g_{v, j + 1 \sim n}$ 更新答案。等价于对每个 $g_{v, j}$ ，用 $g_{v, j} + max f_{u, 1 \sim j - 1}$ 更新答案。线段树合并时维护 $f_{u}$ 前缀和即可。

每次合并一个儿子之前，算出它和已经合并的所有儿子之间的贡献，即可考虑到所有儿子之间的贡献。

时间复杂度 $O (n \log n)$ 。代码。

[模拟赛] 博弈问题

给定一棵以 $1$ 为根的树，点有点权 $w_{i}$ 。对每个结点 $u$ 求 $max_{x \in subtree (u)} min_{y \in subtree (v) \land x \neq y} w_{x} \oplus w_{y}$ 。

$1 \leq n \leq 10^{5}$ ， $0 \leq w \leq 10^{5}$ 。2s，512MB。

异或最小值考虑 01 Trie。

尝试对 01 Trie 上的每个区间维护答案式。注意到对于当前区间，若左右子树大小均大于 $1$ ，则区间答案必然被限制在左右子树内。因为若 $x, y$ 分别在不同子树，则答案的这一位为 $1$ ，但无论 $x$ 在左子树还是右子树， $y$ 都可以和 $x$ 在相同子树，使得答案这一位为 $0$ 。否则我们尝试用大小等于 $1$ 的子树内唯一的那个数在另一个子树内查找异或最小值，然后更新答案。

一次 push_up 的时间复杂度为 $O (\log n)$ 。对于每个点求答案只需要 01 Trie 合并即可，时间复杂度线性对数平方。

P4577 [FJOI2018] 领导集团问题

设 $f_{i, j}$ 表示以 $i$ 为根的子树 $min w \geq j$ 的答案。合并 $i$ 及其子节点 $u$ 时，令 $f_{i, j} \leftarrow f_{i, j} + f_{u, j}$ 。

合并完儿子后，还要令 $f_{i, j} \leftarrow max (f_{i, j}, f_{i, w_{i}} + 1)$ （ $j \leq w_{i}$ ），表示往部门中加入结点 $i$ 。

考虑对上述转移方程使用整体 DP，但无法合并： $max a_{i} + max b_{i} \neq max (a_{i} + b_{i})$ 。

$f$ 单调不降，所以每次取 $max$ 相当于区间 $+ 1$ 。线段树合并维护 $f$ 的差分数组（ $f_{i, j} - f_{i, j + 1}$ ），借助线段树二分求出区间加的范围。

时间复杂度 $O (n \log n)$ 。代码。

CF1051G Distinctification

注意到一个数左移和右移贡献抵消，故可以将一段连续的 $a_{i}$ 全部移到最左边，再将代价小的尽量往右移。

左移贡献：对每一段连续的 $a_{i}$ 维护 $\sum a_{i} b_{i}$ ， $\sum b_{i}$ 和 $min a_{i}$ ，则贡献为 $(min a_{i}) (\sum b_{i}) - \sum a_{i} b_{i}$ 。
右移贡献：用线段树维护 $b_{i} \times k_{i}$ ，其中 $k_{i}$ 表示 $b_{i}$ 在这一段 从大到小 的排名 $- 1$ 。

用并查集维护每个连续段。新加入 $(a_{i}, b_{i})$ 时，先减去 $a_{i}$ 所在连续段原来的贡献，更新后再加上。接下来判断能否连通两端的连续段：

若 $a_{i} - 1$ 处存在连续段，连通之。
强制连通 $a_{i}$ 与所在连续段的右边界 $r$ ，因为右移过程最大位置可以达到 $r$ 。
若 $r + 1$ 处存在连续段，连通之。

如果不判断 $a_{i} - 1$ 或 $r + 1$ 是否存在连续段就合并，则会错误地合并 $[1, 2]$ 和 $[4, 5]$ 。

合并时也是先减去每个连续段的贡献，合并后再加上。注意 $a_{i}$ 不受 $n$ 的限制，所以并查集要预处理满。

时空复杂度线性对数，代码。

CF671D Roads in Yusland

考虑树形 DP，设 $f_{i}$ 表示覆盖 $i$ 的子树的最小代价。

具体的覆盖方案并不重要，只有路径顶部深度最小值有影响，因此再记录一维 $j$ 表示之。

考虑合并 $i$ 及其子结点 $u$ ，根据实际意义得到 DP 转移式

f_{i, j}^{'} = min (f_{i, j} + min f_{u, k}, f_{u, j} + min f_{i, k})

若 $j > d e p_{i}$ ，则 $f_{i, j} = + \infty$ 。

设 $v_{i}$ 表示 $min f_{i, k}$ ， $v_{u}$ 表示 $min f_{u, k}$ ，使用线段树合并维护转移：

若 $f_{i}$ 在当前区间有值， $f_{u}$ 没有值，则给该区间加 $v_{u}$ 。
若 $f_{u}$ 在当前区间有值， $f_{i}$ 没有值，则给该区间加 $v_{i}$ 。
若 $f_{i}$ 和 $f_{u}$ 在当前区间均有值，根据线段树合并的性质，只需考虑叶子（非叶子会继续递归合并），因此 $f_{i, j}$ 更新为 $min (f_{i, j} + v_{u}, f_{u, j} + v_{i})$ 。

合并结束后考虑所有以 $i$ 为较深端的路径 $(a, i, w)$ ，用 $w + {min}_{p = d e p_{i}}^{d e p_{a}} f_{i, p}$ 尝试更新 $f_{i, d e p_{a}}$ 。最终若 $f_{1, d e p_{1}} \neq + \infty$ 则有解，答案为 $f_{1, d e p_{1}}$ ，否则无解。

时间复杂度 $O (n \log n)$ 。注意空间比较卡。代码。

P5298 [PKUWC2018] Minimax

设 $f_{i, j}$ 表示 $i$ 的权值为 $j$ 的概率。

对于叶子， $f_{i, w_{i}} = 1$ ，其它 $f_{i, j}$ 均为 $0$ 。

对于只有子结点 $u$ 的 $i$ ， $f_{i} = f_{u}$ 。

对于同时拥有两个子结点 $u, v$ 的 $i$ ，则有 $f_{u, a} f_{v, b}$ 以 $p$ 的概率贡献至 $f_{i, max (a, b)}$ ，以 $1 - p$ 的概率贡献至 $f_{i, min (a, b)}$ 。

考虑直接枚举 $f_{i, j}$ ，则若 $f_{u, j}$ 有值，则 $f_{i, j} = f_{u, j} (p \sum f_{v, 1 \sim j - 1} + (1 - p) \sum f_{v, j + 1 \sim max w_{i}})$ ，对于 $f_{v, j}$ 同理。

线段树合并维护转移，每个区间维护对应 $\sum f_{i, j}$ 。按下标从小到大合并，维护当前 $\sum f_{u, 1 \sim k}$ 和 $\sum f_{v, 1 \sim k}$ ，遇到一侧空结点时给另一侧打乘法懒标记。

时间复杂度 $O (n \log n)$ 。代码。

*P6773 [NOI2020] 命运

假设 $x$ 子树内所有边的方案已经确定。

对于 $v$ 端在 $x$ 子树内（包含 $x$ ）， $u$ 端为 $x$ 祖先的未被满足的限制 $(u, v)$ ，在确定其它边的方案时，若 $u$ 最深的限制被满足，则所有限制都被满足。

因此，设 $f_{x, j}$ 表示 $v$ 端在 $x$ 子树内， $u$ 端为 $x$ 祖先的未被满足的限制 $(u, v)$ 的 $u$ 的最大深度为 $j$ 的方案数。若 $u$ 不存在则 $j = 0$ 。

初始化 $f_{x, d} = 1$ ，其中 $d$ 表示 $v_{i} = x$ 的 $u_{i}$ 深度最大值。

合并 $x$ 及其子结点 $y$ 时：

若 $(x, y)$ 不选，有 $\sum_{max (k, l) = j} f_{x, k} f_{y, l}$ 贡献至 $f_{x, j}$ ，即 $\sum_{k = 0}^{j} f_{x, j} f_{y, k} + \sum_{k = 0}^{j - 1} f_{x, k} f_{y, j}$ 。
若 $(x, y)$ 选，则有 $\sum_{k = 0}^{n} f_{x, j} f_{y, k}$ 贡献至 $f_{x, j}$ 。

线段树合并时记录 $\sum_{k = 0}^{p} f_{x, k}$ 和 $\sum_{k = 0}^{n} f_{y, k} + \sum_{k = 0}^{p} f_{y, k}$ ，分别为 $f_{y, j}$ 和 $f_{x, j}$ 前的系数，其中 $p$ 表示当前合并到的位置。若某个子树为空则给另一个子树打乘法懒标记。

最后令 $f_{x, d e p_{x}} \leftarrow 0$ 。

下推标记不需要新建结点，因为结点为空说明对应区间 DP 值为 $0$ 。

时间复杂度 $O (n \log n)$ 。代码。

*P5327 [ZJOI2019] 语言

对每个城市，考虑可以与之贸易的城市的形态，发现为经过该城市的路径的并。因为所有路径均经过该城市，所以路径并等价于路径两端形成的虚树。

虚树大小（边数）为所有关键点按时间戳排序并排成环，相邻两结点距离之和的一半。

每个 $s_{i}, t_{i}$ 相当于给路径上所有点的虚树加入关键点 $s_{i}, t_{i}$ ，用线段树合并维护虚树即可。注意用单次询问 $O (1)$ 的 LCA。

时间复杂度 $O ((n + m) \log n)$ 。代码。

*P7963 [NOIP2021] 棋局

破烂码农卡常屑题。

普通道路和直行道路的可达范围很容易刻画，而互通道路形成若干连通块。加入棋子会让互通道路的连通性变得稀碎，很麻烦。考虑将整个过程倒过来，那就是删除棋子，然后连通它周围的互通道路。

考虑只有互通道路的情况。对两种颜色，以等级为下标用线段树维护每个连通块边界上对应颜色的所有棋子，以查询边界上某种颜色的等级不大于某个值的棋子数量。但这样不同棋子可能占用同一个下标，而同一棋子在线段树合并时也在同一个下标。为区分，将每个棋子的等级变成它在所有棋子中以等级为第一关键字，加入时间为第二关键字（同等级，后加入的棋子可以吃前加入的棋子）从小到大的排名。

删除棋子时，其占用的位置变成空地，四周若有空地则连通，若有棋子则加入边界。一开始处理好每个棋子的这些信息。

加入直行道路，对每个位置求出上下左右通过直行道路可达的边界。对每行每列用 set 维护所有棋子的位置，可求出各个方向上走直行道碰到的第一个棋子（或不存在）。

然后减掉直行道路和互通道路同时可达的位置，即查询某个棋子是否在某个互通道路连通块的边界上，以及查询某个 $1 \times x$ 或 $x \times 1$ 的矩形框住的某个互通道路连通块内的空地数量。为此，用线段树维护每个互通道路连通块内所有空地，一棵满足同一行位置的下标连续，如 $(x, y) \to (x - 1) m + y$ ，另一棵满足同一列位置的下标连续，如 $(x, y) \to (y - 1) n + x$ 。

普通道路是平凡的。

设 $n m$ 和 $q$ 同级，时间复杂度 $O (q \log q)$ 。代码。

卡常方向：将合并过程离线建树，在树上 DFS 并用 BIT 维护。不想写了，详见 djq_cpp 的代码。

*CF1344E Train Tracks

若结点 $i$ 在 $t_{1}$ 时刻必须指向 $x$ ，接下来第一次切换儿子的时刻为 $t_{2}$ ，则必须存在时刻 $t \in [t_{1} + 1, t_{2}]$ 使得 $i$ 从指向 $x$ 变成指向 $y$ 。

找出所有这样的时刻区间 $I_{1}, I_{2}, \dots, I_{k}$ ，则问题相当于给每个 $I_{i}$ 分配时刻 $t_{i}$ ，使得 $t_{i}$ 互不相同且 $t_{i} \in I_{i}$ 。这是经典问题。将 $I$ 按照左端点排序，从小到大依次考虑每个时刻 $t$ ，将所有左端点为 $t$ 的区间的右端点加入集合 $S$ ，并取出 $S$ 中最小的元素 $v$ 。若 $v < t$ ，说明不存在一种方案使得右端点在 $v$ 时刻及之前的区间满足条件，即 $v$ 为最晚爆炸时间。得到 $v$ 后容易求出最少切换次数。

问题转化为如何求得这样的 $I_{k}$ 。对于每个结点 $i$ ，设其儿子分别为 $x_{1 \sim u}$ 。设 $S (i)$ 表示目的地在 $i$ 子树内的火车的出发时间集合，则 $S (i) = ⋃_{i = 1}^{u} S (x_{i})$ ，而每个 $S (x_{i})$ 内的元素 $t$ 表示 $t$ 时刻 $i$ 必须指向 $x_{i}$ 。注意到合并两个集合 $S, T$ 时，仅产生 $O (min (| S |, | T |))$ 个新时刻区间。换言之，将元素 $t \in S$ 插入集合 $T$ 时，至多产生 $1$ 个新区间。根据启发式合并的复杂度证明，时刻区间总数 $k = O (m \log n)$ 。

因此，可以直接 LCT 求出所有 $I_{i}$ ，也可线段树合并或启发式合并维护。线段树合并的维护方式：线段树每个下标表示一个时刻，存储的值为其所属儿子结点编号，称为颜色。线段树的每个区间维护该区间第一个有值的位置的第一个与其不同色的后继，这样可以暴力跳后继求得每个 $I_{i}$ 。

总时间复杂度 $O (k \log k + n \log t)$ 。代码。

4. 树套树

前置知识：动态开点线段树。

树套树是在树形数据结构的结点内部套一层树形数据结构。为方便说明，分别记为外层结构和内层结构。

树套树的常见形式有线段树套线段树，树状数组套线段树，以及线段树套平衡树。

4.1 树状数组套线段树

BIT 套动态开点线段树可解决带修二维数点等经典问题。注意当值域过大时需将外层结构换成动态开点线段树。

4.1.1 带修二维数点

修改点权，查询矩形点权和，强制在线。

设 $x$ 的值域为 $[1, n]$ ， $n \leq 10^{5}$ ； $y$ 的值域为 $[1, m]$ ， $m \leq 10^{9}$ 。

对于单点修改， $x$ 在 BIT 上遍历， $y$ 在线段树上修改。相较于普通 BIT，每个结点存储的信息从一段区间所有位置上值的和变成了线段树的和。

对于矩形求和，视为在 BIT 上执行区间 $[x_{l e f t}, x_{r i g h t}]$ 求和，求和内容为线段树在固定区间 $[y_{d o w n}, y_{u p}]$ 上的和。BIT 的区间查询依赖信息可减性。和具有可减性，故正确。

一般地，二维平面可视为若干直线排成一排。将平面剖成 $n$ 条竖直（或水平，取决于哪一维值域更小）的直线，用动态开点线段树维护每条直线的单点修改，区间求和。因为需支持对一段区间（矩形在 $x$ 轴上的区间）的线段树的查询，所以外层也要支持单点修改，区间求和。

每次操作需查询或修改 $\log n$ 个大小为 $m$ 的线段树，所以时间、空间复杂度为 $O (q \log n \log m)$ 。

查询时，对于直接相加的信息，例如满足条件的数的个数或权值之和，可以在遍历 BIT 时直接查询。但如果内层结构查询的形式为 线段树二分，如动态区间第 $k$ 小，就需要把在 BIT 上遍历到的所有位置对应的内层结构的根结点编号 $S$ 记录下来，递归时一并考虑，因为递归方向由这些结点上的信息共同确定。注意递归过程中需实时更新当前查询区间在所有遍历到的内层结构上的对应编号，即令所有 $x \in S$ 变为 $l s_{x}$ 或 $r s_{x}$ 。
若非强制在线，可使用 cdq 分治做到更优秀的复杂度。

4.1.2 动态逆序对

动态逆序对本质上是三维偏序 / 带修点权的二维数点问题。

删除位置 $p$ 上的元素时，需要知道有多少未被删去的元素和它组成逆序对。即位置小于 $p$ ，数值大于 $a_{p}$ 且删除时间比它迟的元素个数，以及位置大于 $p$ ，数值小于 $a_{p}$ 且删除时间比它迟的元素个数。三条限制分别对应三个维度的偏序关系，可以 cdq 分治。

从二维数点的角度出发，就是将 $(i, a_{i})$ 看成平面上的点。删除 $p$ 时查询 $x$ 坐标范围 $[1, i - 1]$ ， $y$ 坐标范围 $[a_{i} + 1, n]$ 的矩形点数，以及矩形 $[i + 1, n] \times [1, a_{i} - 1]$ 的点数。前者统计在 $a_{i}$ 之前比 $a_{i}$ 大的数的个数，后者统计在 $a_{i}$ 之后比 $a_{i}$ 小的数的个数。然后将 $(i, a_{i})$ 从平面上删去，相当于点权置为零。

两种方法的时间复杂度均为 $O (n \log^{2} n)$ 。前者离线（需要知道每个点被删除的时间）但空间复杂度线性，后者在线但空间复杂度 $O (n \log^{2} n)$ 。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1e5 + 5;
constexpr int K = N << 9;
int n, m, node, a[N], rev[N], R[N], ls[K], rs[K], val[K];
long long ans;
void modify(int l, int r, int p, int &x, int v) {
  if(!x) x = ++node;
  val[x] += v;
  if(l == r) return;
  int m = l + r >> 1;
  if(p <= m) modify(l, m, p, ls[x], v);
  else modify(m + 1, r, p, rs[x], v);
}
int query(int l, int r, int ql, int qr, int x) {
  if(ql <= l && r <= qr) return val[x];
  int m = l + r >> 1, ans = 0;
  if(ql <= m) ans = query(l, m, ql, qr, ls[x]);
  if(m < qr) ans += query(m + 1, r, ql, qr, rs[x]);
  return ans;
}
void add(int x, int y, int v) {while(x <= n) modify(1, n, y, R[x], v), x += x & -x;}
int query(int x, int yd, int yu) {int s = 0; while(x) s += query(1, n, yd, yu, R[x]), x -= x & -x; return s;}
int query(int xl, int xr, int yd, int yu) {return yd > yu ? 0 : query(xr, yd, yu) - query(xl - 1, yd, yu);}
int main() {
  cin >> n >> m;
  for(int i = 1; i <= n; i++) cin >> a[i], rev[a[i]] = i, add(i, a[i], 1);
  for(int i = 2; i <= n; i++) ans += query(1, i - 1, a[i] + 1, n);
  for(int i = 1, p; i <= m; i++) {
    cin >> p, p = rev[p], cout << ans << "\n";
    ans -= query(1, p - 1, a[p] + 1, n) + query(p + 1, n, 1, a[p] - 1)；
    add(p, a[p], -1);
  }
  return 0;
}

4.1.3 区间动态第 $k$ 小

主席树带修是什么概念？区间第 $k$ 小从静态变为动态，只需将可持久化线段树换成树套树。

回忆使用主席树求静态区间第 $k$ 小的过程。我们做线段树关于下标的前缀和，用 $T_{r}$ 减去 $T_{l - 1}$ 得到当前区间 $[l, r]$ 包含的元素形成的权值线段树 $T_{l, r}$ 。求第 $k$ 小只需在 $T_{l, r}$ 上二分。

带修前缀和自然考虑树状数组。树状数组每个位置上存储的值变成线段树。因为 BIT 将信息前缀和摊到了它的 $O (\log n)$ 个结点上，所以前缀 $[1, r]$ 对应的线段树 $T_{r}$ 变成了 BIT 上若干结点存储的线段树之和。 $T_{l - 1}$ 同理。

因此，设 $[1, r]$ 在 BIT 上分解得到的结点的对应线段树的根结点集合为 $A d d$ ， $[1, l - 1]$ 为 $S u b$ 。线段树上二分时考虑 $A d d$ 和 $S u b$ 的贡献。

设 $v = \sum_{x \in A d d} v_{l s (x)} - \sum_{x \in S u b} v_{l s (x)}$ ，则 $v$ 表示下标 $[l, r]$ 中权值落在当前权值区间 $[L, R]$ 左儿子所表示区间 $[L, M]$ 的数的个数。若 $k \leq v$ 则区间第 $k$ 小落在 $[L, M]$ ，向左子区间 $[L, M]$ 递归，并令 $A d d$ 和 $S u b$ 所有结点变成它的左儿子。否则 $k$ 减去 $v$ ，向右子区间 $[M + 1, R]$ 递归，并令 $A d d$ 和 $S u b$ 所有结点变成它的右儿子。

时间、空间复杂度均为 $O (q \log n \log V)$ ，其中 $V$ 是值域。离散化后为 $O (q \log^{2} n)$ 。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1e5 + 5;
constexpr int K = N << 9;
int n, m, node, a[N], R[N], ls[K], rs[K], val[K];
void modify(int l, int r, int p, int &x, int v) {
  if(!x) x = ++node;
  val[x] += v;
  if(l == r) return;
  int m = l + r >> 1;
  if(p <= m) modify(l, m, p, ls[x], v);
  else modify(m + 1, r, p, rs[x], v);
}
vector<int> Add, Sub;
int query(int l, int r, int k) {
  if(l == r) return l;
  int m = l + r >> 1, v = 0;
  for(int it : Add) v += val[ls[it]];
  for(int it : Sub) v -= val[ls[it]];
  for(int &it : Add) it = k <= v ? ls[it] : rs[it];
  for(int &it : Sub) it = k <= v ? ls[it] : rs[it];
  if(k <= v) return query(l, m, k);
  return query(m + 1, r, k - v);
}
void add(int x, int y, int v) {
  while(x <= n) modify(0, 1e9, y, R[x], v), x += x & -x;
}
int main() {
  cin >> n >> m;
  for(int i = 1; i <= n; i++) cin >> a[i], add(i, a[i], 1);
  for(int i = 1, l, r, k; i <= m; i++) {
    char op;
    cin >> op >> l >> r;
    if(op == 'C') add(l, a[l], -1), add(l, a[l] = r, 1);
    else {
      cin >> k, Add.clear(), Sub.clear();
      int x = r;
      while(x) Add.push_back(R[x]), x -= x & -x;
      x = l - 1;
      while(x) Sub.push_back(R[x]), x -= x & -x;
      cout << query(0, 1e9, k) << "\n";
    }
  }
  return 0;
}

4.2 线段树套线段树

线段树套线段树也称二维线段树，是信息不具有可减性时树状数组套线段树的替代品，如查询矩形内点权最值。使用方法是把外层结构从树状数组换成线段树。

二维线段树的外层线段树不支持 push_up。因此，修改外层线段树的时候必须快速计算一个不一定包含当前区间的修改对当前区间的影响，即 不 push_up，而是根据修改立刻计算新的信息，此时修改区间不一定完全包含当前区间。这对信息和修改的性质要求极高。

例如矩形 $[x_{l}, x_{r}] \times [y_{l}, y_{r}]$ 范围内所有点加 $1$ ，外层线段树维护横坐标，则修改对外层线段树上对应横坐标区间为 $[l, r]$ 的结点所维护的关于纵坐标的线段树的影响为 $[y_{l}, y_{r}]$ 区间加 $| [l, r] \cap [x_{l}, x_{r}] |$ 。

注：该算法出题的概率极小，所以接下来的内容不看或看不懂也没关系。

对于外层的区间修改，因为不能 push_down，所以必须标记永久化。

对于矩形修改矩形查询，我们往外层 递归路径上所有区间 的信息 $v a l$ 加入内层修改（必须直接算出修改后的 $v a l$ ），往外层 拆分区间 的标记 $l a z$ 加入内层修改。注意外层的每个 $v a l$ 和 $l a z$ 都是一棵线段树。查询时，合并外层递归路径上所有 $l a z$ 的内层区间的信息，和当前拆分区间的 $v a l$ 的内层区间的信息。

这要求先合并所有位置上的信息和所有位置上的标记，再合并信息和标记，等价于先合并每个位置的信息和对应的标记，再将所有位置的结果合并，因为实际结果是后者，而我们只能做到前者。例如， $max a_{i} + max b_{i}$ 不一定等于 $max (a_{i} + b_{i})$ ，但 $max (max a_{i}, max b_{i})$ 一定等于 $max (max (a_{i}, b_{i}))$ 。

例如矩形取 $max$ ，矩形求 $max$ 。修改时将递归路径上所有 $v a l$ 的内层区间对修改值取 $max$ ，再将拆分区间维护的 $l a z$ 的内层区间对修改值取 $max$ 。查询时求递归路径上所有 $l a z$ 的内层区间最大值的 $max$ ，再与拆分区间维护的 $v a l$ 的内层区间最大值取 $max$ 。

4.3 例题

P4390 [BOI2007] Mokia 摩基亚

二维数点板子题，使用树套树或 CDQ 分治解决。

时间复杂度 $q \log^{2} w$ 。

*P3437 [POI2006] TET-Tetris 3D

使用标记永久化的线段树套线段树维护矩形取最大值矩形求最大值，时空复杂度 $O (n \log S \log D)$ 。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1e3 + 5;
int n, D, S;
namespace ST {
  int node, val[N << 11], laz[N << 11], ls[N << 11], rs[N << 11];
  void modify(int l, int r, int ql, int qr, int &x, int v) {
    if(!x) x = ++node;
    laz[x] = max(laz[x], v);
    if(ql <= l && r <= qr) return val[x] = max(val[x], v), void();
    int m = l + r >> 1;
    if(ql <= m) modify(l, m, ql, qr, ls[x], v);
    if(m < qr) modify(m + 1, r, ql, qr, rs[x], v);
  }
  int query(int l, int r, int ql, int qr, int x) {
    if(!x) return 0;
    if(ql <= l && r <= qr) return max(laz[x], val[x]);
    int m = l + r >> 1, ans = val[x];
    if(ql <= m) ans = max(ans, query(l, m, ql, qr, ls[x]));
    if(m < qr) ans = max(ans, query(m + 1, r, ql, qr, rs[x]));
    return ans;
  }
}
int laz[N << 2], val[N << 2];
void modify(int l, int r, int ql, int qr, int u, int d, int x, int v) {
  ST::modify(1, S, u, d, laz[x], v);
  if(ql <= l && r <= qr) return ST::modify(1, S, u, d, val[x], v), void();
  int m = l + r >> 1;
  if(ql <= m) modify(l, m, ql, qr, u, d, x << 1, v);
  if(m < qr) modify(m + 1, r, ql, qr, u, d, x << 1 | 1, v);
}
int query(int l, int r, int ql, int qr, int u, int d, int x) {
  int ans = ST::query(1, S, u, d, val[x]);
  if(ql <= l && r <= qr) return max(ans, ST::query(1, S, u, d, laz[x]));
  int m = l + r >> 1;
  if(ql <= m) ans = max(ans, query(l, m, ql, qr, u, d, x << 1));
  if(m < qr) ans = max(ans, query(m + 1, r, ql, qr, u, d, x << 1 | 1));
  return ans;
}
int main() {
  cin >> D >> S >> n;
  for(int i = 1; i <= n; i++) {
    int d, s, w, x, y; cin >> d >> s >> w >> x >> y;
    int ht = query(1, D, x + 1, x + d, y + 1, y + s, 1);
    modify(1, D, x + 1, x + d, y + 1, y + s, 1, ht + w);
  }
  cout << query(1, D, 1, D, 1, S, 1) << endl;
  return 0;
}

P5445 [APIO2019] 路灯

考虑点亮路灯 $p$ ，找到该路灯左右第一个灭着的路灯 $x, y$ ，那么改变状态的点对为 $a \in [x + 1, p]$ 以及 $b \in [p + 1, y]$ ，它们从不可行变成可行。熄灭路灯同理。

对于一个点对，它的贡献为所有可行的时刻连续段 $[l_{i}, r_{i}]$ 的 $\sum (r_{i} - l_{i})$ 之和。拆成在点亮时减去 $l_{i}$ ，熄灭时加上 $r_{i}$ 。注意若当前时刻 $t$ 可行，则还需要加上当前时刻（因为只有 $- l_{i}$ ，要强制令 $r_{i} = t$ ）。

点对问题转化为平面问题，矩形加单点查询。

时空复杂度 $O (q \log^{2} n)$ 。代码。

P3688 [ZJOI2017] 树状数组

题目给出的代码维护的是序列后缀和，因此结果正确当且仅当 ${\begin{cases} a_{l - 1} = a_{r} & (l > 1) \\ a_{r} = 0 & (l = 1) \end{cases}$ 。

设 $f_{x, y}$ 表示 $a_{x} \neq a_{y}$ 的概率（ $x < y$ ），则一次操作 $[l, r]$ 产生的影响为：设 $p = \frac{1}{r - l + 1}$ ，则

对于 $x < l \leq y \leq r$ ，有 $p$ 的概率翻转 $a_{y}$ 。因此，将 $f_{x, y}$ 变成 $f_{x, y} (1 - p) + (1 - f_{x, y}) p$ 。
对于 $l \leq x, y \leq r$ ，有 $2 p$ 的概率翻转 $a_{x}$ 或 $a_{y}$ 之一。
对于 $l \leq x \leq r < y$ ，有 $p$ 的概率翻转 $a_{x}$ 。

将 $(x, y)$ 看成点，一次操作对平面上三个矩形的 $f$ 产生影响，树套树维护即可。

时空复杂度 $O (q \log^{2} n)$ 。代码。

posted @ 2024-08-13 10:33 qAlex_Weiq 阅读(2389) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 线段树的高级用法

· 字符串基础

· 线段树总集

· 浅谈线段树

· 线段树 & 树状数组

阅读排行：
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布：重大改进与新特性概览！
· .NET10 - 预览版1新功能体验（一）

公告

昵称： qAlex_Weiq
园龄： 4年3个月
粉丝： 917
关注： 56

+加关注

2025年3月

日

一

二

三

四

五

六

1. 常见技巧

1.1 信息设计

1.2 抽象线段树

1.3 维护历史信息

1.3.1 历史最值

1.3.2 历史和

1.3.3 矩阵乘法与历史和

1.4 动态开点

1.5 标记永久化

1.6 线段树二分

1.6.1 全局查询

1.6.2 区间查询

1.6.3 具体实现

1.7 例题

*CF765F Souvenirs

*CF671E Organizing a Race

2. 可持久化线段树

2.1 算法简介

2.2 应用

2.3 扩展

2.3.1 可持久化数组

2.3.2 可持久化树状结构

2.3.3 可持久化并查集

2.4 例题

*P2839 [国家集训队] middle

*CF453E Little Pony and Lord Tirek

3. 线段树合并

3.1 算法介绍

3.2 应用

3.3 线段树分裂

3.4 例题

*P3521 [POI2011] ROT-Tree Rotations

[模拟赛] 博弈问题

*P6773 [NOI2020] 命运

*P5327 [ZJOI2019] 语言

*P7963 [NOIP2021] 棋局

*CF1344E Train Tracks

4. 树套树

4.1 树状数组套线段树

4.1.1 带修二维数点

4.1.2 动态逆序对

4.1.3 区间动态第 k 小

4.2 线段树套线段树

4.3 例题

*P3437 [POI2006] TET-Tetris 3D

公告

搜索

常用链接

最新随笔

随笔档案 (85)

4.1.3 区间动态第 $k$ 小