抽象代数课程笔记 III —— 域论、伽罗瓦理论
Chap.13 Field Theory
Sec.13.1 Basic Theory and Field Extensions
基本概念
一些基本定义和域论最重要的概念:域扩张。
特征
域
对于整环
记
结论 13.1
证明
若
且 ,则 ,于是 或 。
。
例
(1)
。 (2)
。
素域
素域是
例
(1)
的素子域为 。 (2)
的素子域同构于 。
扩域
若域
若
度
是 的线性空间,若 : (1)
上的加法形成阿贝尔群。 (2)
。 (3)
。 (4)
。 (5)
。 存在
上的一组基底,使得 的每个元素由这些基底的 -线性组合得到。基底的大小即扩张的度。
例
,基底为 。
有限扩张
若
一类特殊扩域:不可约多项式的根
尝试求解
结论 13.2(推论 7.10)
设
定理 13.3
设不可约多项式
证明
设
。因为 不可约,所以 是域(结论 9.15)。 考虑
的自然映射 。设 (映射 的原像集为 的部分),则 是同态。因为 ,所以 不为零, 是单射, 。将 对应于 ,则 是 的子域。 因为
是同态,所以 ,其中 。
在 上可能没有根,但在 上一定有根:如果 上的元素不能满足要求,那就让变量 本身成为一个元素。
就是通过 根据 扩张得到的。 在 上没有根。考虑 ,此时 本身就是一个元素,即 。对于 ,有 恰好对应复数乘法。这不是巧合,只是一种视角将
视作 ,另一种视角将 视作模 下的 。它们本质相同。
现在考虑如何用
定理 13.4
设
恰为所有度小于
注:使用
证明
由
上的带余除法, ,其中 。因此,所有 的等价类可以表示为度小于 的关于 的多项式, 确实张成了 。 若
线性相关,则根据线性关系得到 上的非零多项式 且 ,矛盾。
将定理放在
上就容易理解了:对度为 的多项式 ,所有度小于 的多项式在模 意义下互不相同,所有度不小于 的多项式模 最终得到度小于 的多项式。 对于所有度小于
的多项式,它们可以表示为 ,其中 ,于是 由 的 -线性组合得到。此外, 的不可约性保证 是一个域。
另一种角度:设
将等式两侧同时乘以
推论 13.5
设
根的生成域
生成域
设
最小域的存在性由两个域的交集是域保证。
单扩张、本原元
若
计算单扩张的基底和度:往
定理 13.6
设不可约多项式
证明
构造自然映射
,其中 。 因为
,所以 ,导出同态 (直接映射和先模 再映射的结果相同)。因为 不可约,所以 是域, 是域同态。因为 不是零映射,所以 是单射。 因为像集包含
和 且为 的子域,由定义,像集为 ,即 是满射。
定理 13.3 保证含根扩域的存在性,定理 13.4 描述了该扩域的形态,定理 13.6 证明了该扩域的最小性。
不可约多项式的所有根在代数上不可区分 (algebraically indistinguishable)。任选一个根,得到的域相互同构。核心是
推论 13.7
设定理 13.6 的不可约多项式
该推论结合推论 13.5 描述了当
不可约多项式不同的根具有相同的代数性质可以扩展为定理 13.8。
定理 13.8
设
证明
将 上的极大理想 映为 上的极大理想 。取商,得到域同构 由定理 13.6,
, 。复合所有同构得到 。
该定理(及其推广定理 13.27)频繁应用于 Galois 理论。
作业
练习 13.1.1
设
解
由
上的带余除法, 代入
, 因此
解方程法见下一题。
练习 13.1.2
设
解
设
,则 比较系数得方程组
解得多项式
。因此 如果使用带余除法,则需要两次。
Sec.13.2 Algebaric Extensions
设
代数元及其最小多项式
上节的内容是根据不可约多项式构造扩域包含多项式的根。本节我们希望由扩域上的根确定相对应的多项式,并以此导出单扩张的性质。首先需要排除扩域上不是根的元素,仅保留代数元。
代数、超越
称
若
代数扩张
若多项式
结论 13.9
设
直观认知:
上的带余除法。 证明
设
是度最小的以 为根的多项式。总可以将 乘以常数使得 是首一多项式。 若
在 上可约,则 ,其中 。这与 度最小矛盾。因此 不可约。 设
。由 上的带余除法,存在 使得 ,则 。若 ,则由 导出矛盾。于是 整除任何 上以 为根的多项式。这同时证明了 的唯一性。
最小多项式
结论 13.9 的
推论 13.10
设
上以 为根的多项式也是 上以 为根的多项式,因此 上的最小多项式不会更大。
结论 13.11
设
该结论由定理 13.6 直接得到。
例
(1)
在 上的最小多项式为 , 。 (2)
在 上的最小多项式为 , 。
从通过多项式构造含根的域,到给定根(的性质)直接构造含根的域。
代数扩张的度的性质
注意到
结论 13.12
证明
若
代数,则单扩张的度为 的最小多项式的度。 若
有限,则 个元素 线性相关,因为度为 的扩张最多挑出 个线性无关的元素。存在非零多项式 , 代数。
再次强调,将扩域看成线性空间的视角非常重要。
推论 13.13
若
对
, 是 的子域。
注:结论的逆命题不成立 —— 存在无限代数扩张。但若
定理 13.14
设
证明
设
是 在 上的一组基, 是 在 上的一组基,则 是 在 上的一组基:若 ,即 ,则由 线性无关知 ,由 线性无关知 。
有限扩张的有限扩张是有限扩张。
推论 13.15
设
例
对应最小多项式
。
有限生成扩张、复合域
有限生成
称
喜闻乐见的有限生成时刻。
引理 13.16
即多个元素的生成域可由一系列单扩张得到。
例
其中
是因为 在 上不可约( )。 的基底为 。
定理 13.17
证明
若
有限,设 为 关于 的线性空间的基。由推论 13.15, 整除 。由结论 13.12, 在 上代数。 反之,设
在 上的度为 , 且 。由引理 13.16, 。由推论 13.10, ,即 。由定理 13.14, 。
直观认知:包含超越元的扩张一定是无限扩张。
推论 13.18
若
证明
由定理 13.17,
有限。由推论 13.13, 代数。
推论 13.19
设
由前一推论,代数元关于四则运算封闭,故构成域。
定理 13.20
若
多项式复合即可证明。
复合域
设
若
结论 13.21
设
等号成立当且仅当其中一个域的基底在另一个域线性无关。
推论 13.22
设
作业
练习 13.2.1
设有限域
证明
因为
,所以 的基域为 。因为 是 上的线性空间,设 ,则 是正整数且 。
练习 13.2.3
计算
解
若实多项式
以 为根,则 以 为根。因此考虑 由 Eisenstein 判别法,
不可约。
练习 13.2.7
证明
证明
因为
,所以 。 考虑到
,所以 。因此 。因此 。 令
,计算 ,均表示为 的形式。设 ,解得多项式 。
注:学习 Galois 理论后,我们知道
练习 13.2.11(2)
计算
解
,所以 是 的根。由 Eisenstein 判别法, 不可约,所以 。
练习 13.2.14
设
证明
因为
,所以 。 在 上是 的根,所以 。因为 是奇数,由定理 13.14, 不可能是偶数,所以 。
*练习 13.2.17
设
证明
设
是 的不可约因子 的根, , ,则 且 。因为 且 ,所以 是 的倍数,即 。
Sec.13.4 Splitting Fields and Algebraic Closures
由之前的讨论,存在含
分裂域、正规扩张
分裂域是 Galois 理论的重要概念。
分裂域
扩域
定理 13.25
对任何域
简单归纳 ,每次消去一个因子。
例
(1)
在 上的分裂域为 。 (2)
在 上的分裂域为 。 (3)
的所有根形如 ,其在 上的分裂域为 。
正规扩张
设
注:对有限扩张
结论 13.26
定理 13.27
设
定理 13.8 的推广。本质是定理 13.8 的归纳。
证明
考虑
在 上的不可约分解和 在 上的不可约分解。由 和 同构可知 和 同构,所以不可约分解同构,并通过 联系在一起。 若
完全分解,则 完全分解,取 , , 。这同时证明了 的情形。 使用数学归纳法,假设命题对所有度小于
的多项式成立。 设
是 的度大于 的不可约因子,若不存在则 完全分解,由上述讨论,命题成立。设 为 的对应不可约因子。设 是 的根, 是 的根。由定理 13.8, 且 是 的扩展映射。 设
, , 在 上分解为 , 在 上分解为 ,则 是 在 上的分裂域, 是 在 上的分裂域。由归纳假设,命题成立。
推论 13.28(分裂域的唯一性)
代数闭包
进一步地,我们希望构造一个域包含
代数闭包
代数扩域
代数封闭
称
只要有一个根,就可以不断分解线性因子直到完全分解。
结论 13.29
证明
设
是 的根,则 代数。因为 代数,由定理 13.20, 代数,所以 在 上代数,即 是某个 的根。由代数闭包的定义, ,即 代数封闭。
结论 13.30
对任意
证明较复杂,略去。
结论 13.31
设
我们将借助 Galois 理论证明以下定理(定理 14.35)。
定理(代数学基本定理:Fundamental Theorem of Algebra)
作业
*练习 13.4.2
计算
解
设
,则 的所有根形如 ,其中 且 是落在第一象限的八次单位根。 设
的分裂域为 ,则 。而 ,所以 。因此 ,进而 ,于是 。又因为 包含 的所有根,所以 。因此 。 因为
且 ,所以 。由 Eisenstein 判别法, 在 上不可约,所以 。由定理 13.14, 。
*练习 13.4.5
设
注:不是作业题,但笔者认为值得一做。
证明
设
是 的分裂域。设 是不可约多项式且 ,其中 。设 是 的另一个根。由定理 13.6, 。由定理 13.27, 在 上的分裂域 同构于 在 上的分裂域 。易知 , ,而 ,所以 。于是 ,即 。
因为
是有限扩张,所以 。设 在 上的最小多项式为 ,设 。因为 的某个根 在 上的最小多项式为 的某个不可约因子 ,而 ,所以 在 上完全分解,即 。而所有 均为 的根且 是最小的包含 和 的域,所以 是 的分裂域。
练习 13.4.6
设
(a)
证明
设
是 的分裂域, 是 的分裂域, 是 的分裂域。因为 含 的所有根,所以 。因为 完全分解 和 ,所以 。因此 。
(b)
证明
设
在 上有根,则 在 上有根。由练习 13.4.5, 在 上有所有根,于是 在 上有所有根。由练习 13.4.5, 是 的分裂域。
Sec.13.5 Separable and Inseparable Extension
可分多项式在 Galois 理论中很常见。Galois 理论研究多项式的根,我们将看到多项式有重根和没有重根之间有很大不同。
可分多项式及其判定
单根、重根
在分裂域上,
可分多项式
称
例
(1)
在 上可分,因为它的根 不同。
导数
多项式
乘在
前的 表示 个 相加。
注:这里导数的定义是纯代数的,尽管其和微积分学的导数形式一致,且同样满足线性和乘积的 Leibniz 法则。引入导数完全是为了判定多项式是否含有重根。
结论 13.33
证明
若
,其中 ,则 以 为根。 设
,若 以 为根,则 ,于是 。 后面两条是第一条的直接推论。
例
(1)
在 上可分,因为 。
完美域、可分扩张
在大部分域上,不可约多项式都是可分的。
推论 13.34
在特征为
证明
设度为
的多项式 不可约。因为 ,所以 和 互质。 第二条由第一条和最小多项式的不可约性得到。
要求特征为
以下三条结论证明了推论 13.34 对有限域成立。
结论 13.35
设
因此
推论 13.36
设
大小相同的集合之间的单射是双射。
结论 13.37
推论 13.34 对有限域
证明
设有限域的特征为
, 不可约。 若
,则存在 使得 。设 ,则由结论 13.35, 即
是 的某个多项式的 次幂,这和 不可约矛盾。因此 , 可分。
证明的关键在于利用每个元素都是
完美域
特征为
完美域上的不可约多项式都是可分的。
可分扩张
推论 13.39
完美域的有限扩张是可分扩张。特别地,
可分扩张是 Galois 理论的重要概念。
作业
*练习 13.5.5
对任意质数
注:非常好题目,使我的大脑旋转。
证明
设
, 是 的根。设 ,则 的特征为 。由结论 13.35, 即
是 的根。类似地,所有 都是 的根,其中 。这说明 有 个互不相同的根, 可分。
在 上没有根,否则 是 的根,和 矛盾。这说明 的不可约分解不含线性因子。 设
是 的不可约因子, 是 的根。因为 且 ,所以 ,于是 。这说明 的不可约因子的度相同。又因为 是质数且不存在线性因子,所以不可约因子的度为 ,即 不可约。
Chap.14 Galois Theory
上一章节证明了存在
Galois 理论研究多项式的根的置换群及其分裂域的代数结构之间的关系。当然,对根的置换不能改变分裂域的结构,也不能改变
Sec.14.1 Basic Definitions
设
自同构、固定域
自同构
(1)
(2) 称
恒等映射是自同构,记为
例
任何自同构固定
,所以固定素域。 。
扩张的自同构群
设
结论 14.1
结论 14.2
设
该结论在计算代数扩张的自同构群时极其有用。
例
(1) 设
, ,则 ,因为 是 的两个根。因此 。 (2) 设
, ,则 ,因为 的其它两个根不属于 。因此 。
考虑多项式
结论 14.3
设
验证被固定的元素对四则运算的封闭性。
注:结论对任意
固定域
设
结论 14.4
自同构子群和它们的固定域之间有反包含关系,即
(1) 若
(2) 若
子域越小,越多的自同构固定它。自同构越少,它们固定的元素越多。
Galois 扩张、Galois 群
Galois 理论对自同构数量足够多的扩张更感兴趣。
结论 14.5
设
取等当
证明
对
的大小归纳。 取出
度大于 的不可约因子 ,若不存在则命题显然成立。 现在我们证明
,其中 是 不同根的数量,则 。 设
是 的根, ,则 是 的根。对于 的根 ,如果存在 使得 ,那么:
- 对任意
满足 , ,即 。 - 对任意
, 。 这说明
的 和 一一对应,即使得 的 的数量等于 。 的存在性由定理 13.27 保证。 由归纳假设,
。因此 当
可分时, ,取到等号。
从以上证明可知
注:对任意扩张
Galois 扩张、Galois 群
设
Galois 扩张是有限扩张,因此一定是代数扩张。
推论 14.6
若
多项式的 Galois 群
若
例
(1)
是 Galois 扩张,因为 。 (2)
不是 Galois 扩张,因为 。 (4)
是 Galois 扩张,因为它是可分多项式 的分裂域。其 Galois 群同构于 。 (5)
的分裂域关于 是度为 的 Galois 扩张,其 Galois 群同构于 。
作业
练习 14.1.1
(a) 证明若
(b) 设
显然。
练习 14.1.4
证明
证明
假设存在
到 的同构 ,则 。于是 。考虑到 ,但 在 上无解( 无有理数解),所以这样的 不存在。
练习 14.1.7
(a) 证明对任意
证明
对任意正实数
,设 ,则 ,而 ,所以 。
(c) 证明
证明
若
,则 ,即 保序。 对无理数
,若 ,由有理数的稠密性,存在 使得 ,矛盾。类似地、 。因此 。 。
Sec.14.2 The Fundamental Theorem of Galois Theory
对 Galois 扩张
固定域和 Galois 子群的联系
特征标
群
注:这里的定义是线性特征标。
线性无关
定理 14.7
若
证明
假设
线性相关,设 为非零元素最少的一组系数,则 。 因为
,所以存在 使得 。 由
和
得到非零元素更少的非平凡线性关系
和
的最小性矛盾。
- 选择非零元素最少的非平凡线性关系以导出矛盾是很好用的证明技巧。
引入特征标的目的是得到自同构的线性无关性(推论 14.8)。
嵌入
推论 14.8
若
自同构线性无关限制了自同构的数量。结合
定理 14.9
设
证明
核心:使用自同构线性无关和基底元素线性无关分别排除
和 的情况。 假设自同构的数量大于线性空间的维度,即
。设 是一组基,考虑线性方程组 未知数数量大于方程数量,存在非平凡解
。对任意 ,所有 固定 ,因此 而
的所有元素都可以表示为某个 ,与 线性无关矛盾。
假设线性空间维度大于自同构数量,设
线性无关,考虑线性方程组 未知数数量大于方程数量,存在非平凡解
。 因为
,所以存在 ,否则由 ,存在非平凡线性组合 ,矛盾。 设
为非零元素个数 最小的一组解,不妨设 非零, (将所有方程除以 )且 ,则 因为
且 是固定域,所以存在 使得 。将 作用于每个方程,得 因为
形成群,所以 ,即 两个方程组作差,得
得到非零元素更少的非平凡解,矛盾。
注:还不能确定
定理 14.9 相当重要(然而 DDL 上课根本没讲,因为没时间)。它揭示了自同构群的大小与扩张维度的关系,是建立 Galois 群的子群和 Galois 扩张的子域之间一一对应关系的重要工具。
推论 14.10
对任意有限扩张
证明
的固定域 包含 ,所以 。 若
是固定域,则由定理 14.9,等号成立。若 不是固定域,则 ,等号不成立。
推论 14.10 给出了
推论 14.11
设
证明
由定义,
。问题在于是否所有固定 的自同构均属于 。 由定理 14.9,
。由推论 14.10, 。而 ,所以 因此
。
这说明
推论 14.12
设
证明
若
,则 固定 ,由推论 14.11, ,同理 ,矛盾。
Galois 理论基本定理
定理 14.13
证明
结论 14.5 证明了可分多项式的分裂域是 Galois 扩张。
设
。设 是不可约多项式 的根,设所有不同的 为 。对任意 ,因为 是群,所以 ,于是集合 和 相同,即 是 的置换。 考虑
,则 作用在 的各项系数上不改变 的根的集合,因此保持 不变,即 的各项系数属于 的固定域。由推论 14.10,固定域恰为 ,因此 。 因为
不可约且以 为根,所以 ,而 以 为根,所以 整除 。又因为 是 的根(结论 14.2),所以 整除 。于是 。这说明 可分且所有根 互不相同,证明了在 上有根的不可约多项式可分且在 上完全分解。 设
是 Galois 扩张, 是一组基。设 是 在 上的最小多项式(Galois 扩张是代数扩张),则由上述证明, 可分且所有根属于 。设 为所有 的乘积去掉重复因子,则 的所有根属于 , 包含 的分裂域。又因为 是 的根,所以 的分裂域包含 。因此 是可分多项式 的分裂域。
定理 14.13 是 Galois 扩张常用且好用的等价条件。
推论
若
恰为 的所有根且 是完美域,则 是 Galois 扩张。 证明
考虑
的最小多项式 ,则 整除 。于是所有不同 的乘积 整除 。 是完美域保证 没有重根,所以 可分。又因为所有 恰为 的根,所以 是可分多项式 的分裂域。
这个推论在证明代数学基本定理时要用。
Galois 共轭、共轭域
设
定理 14.13 的证明告诉我们:在 Galois 扩张
Galois 扩张的等价表述
(1)
(2)
(3)
(4) 有限正规可分扩张。
定理 14.14(Galois 理论基本定理)
设
(1) 设
(2)
(3)
(4)
(5)
证明
推论 14.12 说明从
到 是单射。 设
是 的分裂域,则 是 的分裂域, 是 Galois 扩张。由推论 14.10, 是 的固定域。因此从 到 是满射,于是双射。
除了 (4) 以外的其它四个命题都是显然的。(4) 的证明较复杂,略,可参考 为什么五次方程无根式解。值得指出的是,在证明 (4) 的过程中得出了以下结论:
设
是 的固定域。对于 在 的某个代数闭包 上的固定 的嵌入 , ,因为若 在 上有最小多项式 ,则 是 的根,且 包含 的所有根(定理 14.13)。 设
是 的分裂域,则 是 的分裂域( ,因为 固定 ) 。扩展 得到 (定理 13.27),显然 固定 ,得到结论:任何 的嵌入都是 的固定 的自同构的原像集为 的部分。
Galois 理论基本定理是联系群论和域论的桥梁。
作业
练习 14.2.2
计算
解
设
,则 于是
的最小多项式为 。 更一般的方法是计算
和 ,然后解方程。
练习 14.2.12
计算
解
的两个根为 ,所以 的四个根为 。 因此分裂域为
, 其中
Sec.14.4 Composite Extensions and Simple Extensions
为最终的定理准备前置结论:Galois 扩张的交和复合依然是 Galois 扩张。
Lecture notes 没有该小节,但是课上讲了。
Galois 扩张的交和复合
结论 14.19
设
同构于
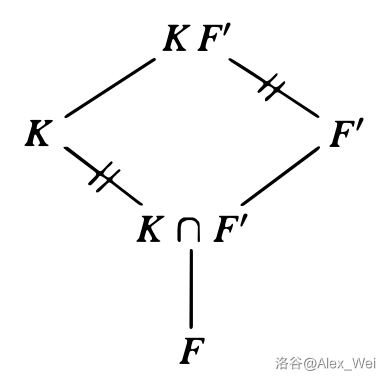
证明
当
时显然。 若
是 Galois 扩张,则 是可分多项式 的分裂域。因为 不包含于 ,所以 是 的分裂域, 是 Galois 扩张。 因为
是 Galois 扩张,所以任何 的固定 的嵌入都是 的自同构(由上一小节最后的结论)。因此 良定义,其中 。 的元素保持 和 不变,所以 , 是单射。 设
为 的像集, 为其固定域,则 。又因为 被 固定,由基本定理, ,即 ,于是 。因此 。由基本定理, 。
非常像第二同构定理。
推论 14.20
设
结论 14.21
设
(1)
(2)
证明
(1) 设
在 上有根 ,由定理 14.13, 的所有根属于 和 ,因此属于 ,即 是 Galois 扩张。 (2) 设
是 的分裂域, 是 的分裂域,则 是 去掉重复因子后得到的多项式的分裂域。对后半部分,构造映射 ,使用推论 14.20 证明 恰为像集。具体证明略。
Galois 扩张的交和复合都是 Galois 扩张。
推论 14.22
设
反之,若
Galois 闭包
推论 14.23
设
的包含 的 Galois 扩张显然存在,如 关于 的线性空间的所有基底的最小多项式的乘积(可分,因为 是可分扩张)的分裂域。最小性使用结论 14.21 即可。
Galois 闭包
推论 14.23 中的
可分扩张的 Galois 闭包存在。
Sec.14.6 Galois Groups of Polynomials
回忆:可分多项式
对 Galois 扩张
注意:这比 Cayley 定理更强。Cayley 定理只保证任何群是
例
(1)
。由 Cayley 定理, 是 的子群。 (2) 在
上 。
若
由结论 14.2,
逆 Galois 问题 (open problem)
任何有限群都是某个多项式在
上的 Galois 群吗?
以上讨论了可分多项式的 Galois 群的大致形态,帮助我们简化计算 Galois 群的结构。本小节的内容是证明一般
初等对称多项式、一般多项式
初等对称多项式
设
定义,即
一般多项式
度为
其所有根为变量
将所有根视作独立变量能够避免特定多项式的特殊性质使得根与根之间产生联系。直观认知:根之间的联系越少,Galois 群越大。
因为
在置换
结论 14.30
对称多项式
有理多项式
等价表述为多项式在
推论 14.31(对称多项式基本定理)
任何
例
(1)
。 (2)
。
这个推论解释了为什么
我们先定义了独立变量
对于一般多项式
设其根为
定理 14.32
一般多项式
在
定理表明,若
高次方程无根式 通解 的前置定理。
判别式
判别式
定义
定义多项式的判别式为其所有根的判别式。若
考虑
对
结论 14.33 和 14.34 是等价表述。
结论 14.33
若
结论 14.34
证明
对
, 当且仅当 固定 ,当且仅当 。
因此,若
代数学基本定理
定理 14.35(代数学基本定理)
所有
证明
首先有以下事实:
(a) 奇数次实多项式有实根,由连续函数介值定理保证。不存在
的非平凡奇度扩张。 (b) 二次复多项式有复根,由二次方程求根公式以及
对开根封闭保证。不存在 的平方扩张。 只需证明所有
在 上有根。 有根当且仅当其复共轭 有根,当且仅当实多项式 有根。因此,只需证明所有 在 上有根。 设实多项式
的度为 ,其中 是奇数。对 进行数学归纳。 当
时,由 (a),命题成立。假设 。 设
为 的根, ,则 是 Galois 扩张(结论 14.13 后面的推论)且 包含 和 的所有根。对任意 ,考虑多项式 任何
的自同构只是对 的排列(由本小节一开始的讨论),所以不改变 。因此 。而 ,其中 是奇数。由归纳假设, 在 上有根,于是存在 使得 。 因为
有限,所以由鸽笼原理,存在不同的实数 使得对某组 , 且 ,则 且 。于是 是 上的二次多项式 的根。由 (b), 。
作业
练习 14.6.4
计算
解
的根为 ,其中 。显然其分裂域为 , 其中
*作业 14.6.6
计算
不太能算,但能证不可约。
证明
在
上考虑 ,得 。 在 上无根,且度为 ,所以不可约。因此,若 可约,则一定有线性因子。但 在 上没有根,因此在 上不可约。由 Gauss 引理, 在 上不可约。
作业 14.6.16
计算
不太能算,但能证不可约。
证明
在
上考虑 ,得 。 在 上无根,且度为 ,所以不可约。因此,若 可约,则一定有线性因子。但 在 上没有根,因此在 上不可约。由 Gauss 引理, 在 上不可约。
Sec.14.7 Solvable and Radical Extensions: Insolvability of the Quintic
本小节的内容是多项式的根的根式解,即使用四则运算和开根号表示多项式的根。最终我们会发现,多项式可由根式解出当且仅当其 Galois 群可解。
用
循环扩张
循环扩张
结论 14.36
设
证明
因为
含 次单位根,所以 是 的分裂域, 是 Galois 扩张。 对任意
, 是 的根,所以 ,其中 是某个 次单位根。容易证明 到 次单位根群 是单射同态。
注:为什么要求
注:为什么是整除
结论 14.37
设
证明
设
是度为 的循环扩张, 。 对任何
次单位根 ,定义 拉格朗日预解式 (Lagrange resolvent) 因为
, 且 ,所以 于是
即
被 固定。
设
是 次本原单位根。由自同构的线性无关性,存在 使得 。此时 即对任意
, 不固定 。由基本定理, 不可能属于任何 的真子域,所以 。又因为 被 固定,所以 ,即 。
结论 14.36 和 14.37 合起来说明基域含所需单位根的循环扩张等价于简单根式扩张。
考虑到有限群
根扩张
假设基域的特征为
根式表示、根扩张
(1) 称在
其中
(2) 称
例
可被根式表示,其中
所有根式扩张都是二次的,所以正
边形可尺规作图。
用四则运算和开根表示多项式的根的精确定义。
引理 14.38
若
证明
首先证明存在
的 Galois 的根扩张。 因为
是可分扩张,所以 在 上的 Galois 闭包 存在。对任意 ,考虑一系列子域 其中
是简单根式扩张 。因为根扩张的复合是根扩张,而所有 的复合恰为 (否则 的复合是更小的 的包含 的 Galois 扩张,和 是 Galois 闭包矛盾),所以 是 的根扩张。
由上,不妨设
是 Galois 根扩张。 首先往
加入根扩张的所有 次单位根得到 ,得到 的根扩张 因为
是 Galois 扩张,所以 是 Galois 扩张(结论 14.21)。 易证
,结合有限生成阿贝尔群基本定理和 Galois 理论基本定理,可知 到 可由一系列循环扩张得到。同时由结论 14.36, 是循环扩张。
Abel-Ruffini 定理
回忆:有限群
满足
定理 14.39
证明
假设
由根式解出,则其每个根包含于满足引理 14.38 的扩张。复合这些扩张得到 ,则 同样满足引理 14.38。 设
是 对应的 的子群。因为 是循环群,所以 可解。又因为 的分裂域是 的子域,所以 的 Galois 群是 的商群,因此 的 Galois 群可解。
假设
的 Galois 群 可解, 为 的分裂域,考虑一系列 的固定域,得到 其中
是度为 的循环扩张。 往
加入所有 次单位根得到 ( 也是简单根式扩张,因为 是 的根),考虑 则
是度整除 的循环扩张(结论 14.19)。现在基域包含了适当的单位根,所以每个循环扩张都是简单根式扩张(结论 14.37)。而 的所有根属于 ,所以 可由根式解出。
推论 14.40
对正整数
“一般” 非常重要,因为一般多项式的 Galois 群是
例
考虑
。由艾森斯坦判据, 不可约,于是其分裂域 的度是 的倍数。 设
,则 且 ,于是存在 。而 唯一的阶为 的元素是五元环,所以 包含五元环。 分析易知
有三个实根,则复共轭 交换剩下两个复根,于是 包含换位。因此 (一个二元环和一个 元环生成 )。
作业
练习 14.7.3
设
的充要条件是 。 证明
若
,则 且 ,所以 。 设
。若 ,则 。于是 ,即 。因为 ,所以存在 使得 。于是 。因为 且 ,所以 。若 ,则 。若 ,则 ,和 矛盾。 解
设
,则 ,即 。 设
,则 ,于是 且 。根据上述结论, 当且仅当 ,当且仅当 。 假设
,其中 ,则 。但 显然不成立,所以 。
*练习 14.7.8
设
证明
假设
,则 ,其中 是 次单位根。
是可分多项式 和 在 上的分裂域,所以 是 Galois 扩张。由结论 14.36, 是循环扩张且度整除 。因为 是质数,所以度为 或 。而 ,所以 ,所以 是度为 的循环扩张, ,其中 。 因为
是 的根,所以 ,其中 是小于 的非负整数。于是 因为
生成 ,所以 固定 。因此 ,矛盾。
*练习 14.7.12
设
证明
由 Cauchy 定理,存在
的子群 满足 ,则其固定域 满足 。 设
是 在 上的最小多项式,易证 是 的分裂域。因为 不可约,所以 作用在 的根的集合 上是传递的,其中 。因为 ,所以存在 ,取 使得 ,则 不含 且 ,于是 。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!