抽象代数课程笔记 I —— 群论
笔记完全基于清华大学邓教授开设的 抽象代数 课程的 Lecture notes 和课本 Abstract Algebra by David S. Dummit。引用部分为个人理解。
抽象代数的意义:
- 对具有结合律的作用的抽象表示,相同的作用只要研究一遍。
- 研究不同作用所共有的性质,发展系统性的手段处理具有特定性质的作用。
- 最终发现特定性质的作用与研究它们的各种手段的广泛应用。
Chap.1 Introduction to Groups
群是具有结合律,存在单位元和逆元的抽象概念,只有作用在集合上才能体现出它的 “作用”。从群作用在集合上导出的对称性和其它性质是研究群的重要手段。事实上,很多群就是由此定义的。因此,很多人说群论是描述对称的理论。
A group is not really about symmetries of a particular object, it's an abstract way that things even can be symmetric. —— Grant Sanderson
Sec.1.1 Basic Axioms and Examples
基本公理。非常基本,必须熟练掌握。
二元运算
集合
- 若
- 若
- 对
二元运算本身不要求结合律或交换律,自由度高。
群公理
集合
(i)
(ii) 存在单位元
(iii) 每个元素存在逆元
群公理暗含了
对 运算的封闭性。 结合律是几乎所有作用的内在性质:函数复合具有结合律。
单位元说明 “什么也不做” 是一种对称。
逆元说明对称作用的逆作用(反悔)也是一种对称(这也是一种对称)。
阿贝尔群
运算具有交换律的群称为 **阿贝尔群 (Abelian Group) **。
简要记号
一般视
对
特殊情况视
结论 1.1(基本性质)
(1) 单位元唯一。
(2) 每个元素的逆元唯一。
(3)
(4)
(5) 广义结合律:
以 (2) 为例:假设
结论 1.2(消去律)
(1)
(2)
以 (1) 为例:
像解方程一样将元素在等式左右移动。
注意:必须同时左乘或同时右乘。
阶
最小的正整数
有没有很熟悉?和数论的阶是同一个概念。模
下的简化剩余系就是群 。
Sec.1.2 Dihedral Groups
基本群之一。
二面体群
考虑所有使正
如果将正
注意:对于
注意:
为什么能构成群?
- 对二面体的作用满足结合律。
- 不进行任何操作也是一种保持形状的作用,它是群的单位元。
- 刚体运动可逆,且保持形状的作用的逆作用保持形状,所以逆元存在。
记
(1)
(2)
(3) 对任意
(4) 对任意
(5)
(6)
注意:作用的复合从右向左,
容易根据实际意义证明这些结论。
(5) 是二面体群最核心的性质,(6) 是 (5) 的直接推论:它揭示了
生成元和关系
二面体群由
为什么要有逆元?阶不一定存在,考虑
。对于有限群则不需要逆元。
由群的封闭性可知
称为
这些关系唯一确定了
寻找一个群的表示是困难的,且表示不一定唯一。
Sec.1.3 Symmetric Group
基本群之二。
对称群
所有
排列就是把集合双射到自身。
对
环表示
环
表示
不交的环是可交换的。
环分解算法
从每个点开始跳出边。OI 基本算法。
一个排列的阶是它的环分解中所有环的环长的最小公倍数。
Sec.1.5 The Quaternion Group
四元数群
满足
乘法的顺序是
Sec.1.6 Homomorphisms and Isomorphisms
群论中最重要的概念。
同态
同态是一个群到另一个群的保持结构的映射。对
或简写为
同构
同构是两个群之间保持结构的映射。映射
表示同构的二元关系符为 \cong)。
同构的意义:
- 同构的群只需要研究其中一个。
- 具有相同性质的群同构。
同态的意义:设
的像集为 。
- 若
是单射,则 存在子结构(子群) 和 同构。 - 若
不是单射,则同态相当于将 “折叠” 成若干几乎和 同构的部分(陪集),每一份在映射后均得到 。引出商群的概念:映射到相同元素的元素坍缩成一个元素,那么 坍缩成和 同构的商群,自然地有第一同态定理 。
同态与表示
对
若
Sec.1.7 Group Actions
群作用在集合上导出的结论一定程度上反映了群本身的结构性质。
群作用
映射
(1)
(2)
即单位元保持元素不动且满足结合律。
作用的排列表示
对每个
(1)
(2) 定义映射
因为
作用在 上得到 的排列,所以 构成的群就是 的若干排列构成的群。不同的 的作用可以相同,所以 不是单射。
反之,给定
将在第四章深入研究群作用。
Chap.2 Subgroups
揭示某种数学对象的结构的基本手段是研究其满足相同公理的子集。
Sec.2.1 Definition and Examples
子群
称
对任意
群判定是一项繁琐的工作,因为需要检查群公理,尤其是结合律。但子群判定只需要检查乘积和逆的封闭性。
子群具有 传递性:若
结论 2.1(子群准则:The Subgroup Criterion)
(1)
(2)
证明:
(2) 将乘积和求逆结合为一条限制。特别地,若
Sec.2.2 Centralizers and Normalizers, Stabilizers and Kernels
一些重要的基本概念的定义。设
中心化子
定义
为
因为
中心
定义
为
因为
正规化子
定义
为
因为
的每个元素和 可交换是 可将 坍缩为 的充要条件,否则存在元素无法和单位元交换。 可以作为商群的陪集当且仅当 ,即 。
群作用的稳定子与核
令
为
定义
为群作用的 核 (Kernel),它是所有
显然
稳定化子,正规化子和中心是子群是稳定子与核是子群的特例。
设
设
考虑
Sec.2.3 Cyclic Groups and Cyclic Subgroups
OIer 最熟悉的一集。
循环群
其中
OI 最常涉及到的循环群是模
意义下的加法群 ,它可以看成加性群 。
结论 2.2
若
(1) 若
(2) 若
结论 2.3
对群
注意
定理 2.4
阶相同的循环群同构。
记
接下来刻画每个元素的阶。
结论 2.5
令
(1) 若
(2) 若
(3) 特别地,若
证明 (2):设
另一方面
所以
相当于求最小的
和 OI 数论中的阶一模一样!它们完全是同一个概念。
结论 2.6
令
(1) 若
(2) 若
定理 2.7
令
(1)
(2) 若
(3) 若
一些情况下有限群和无限群需要分开考虑。
对于 OI 水平较高的读者,Section 2.3 的所有内容应当是非常显然的。
Sec.2.4 Subgroups Generated by Subsets of a Group
给定集合
结论 2.8
如果
集合的生成子群
令
称为 由
当
以及记
定义
即
实际上
结论 2.9
首先有
由
又因为
生成子群的阶
合并相邻相同的元素,得
对阿贝尔群
进一步地,当
若
Sec.2.5 The Lattice of Subgroups of a Group
一种可视化有限群子群关系的结构。
格
用以下方法构建有限群
(1) 写下所有子群,
(2) 若
最终形成入度和出度均为
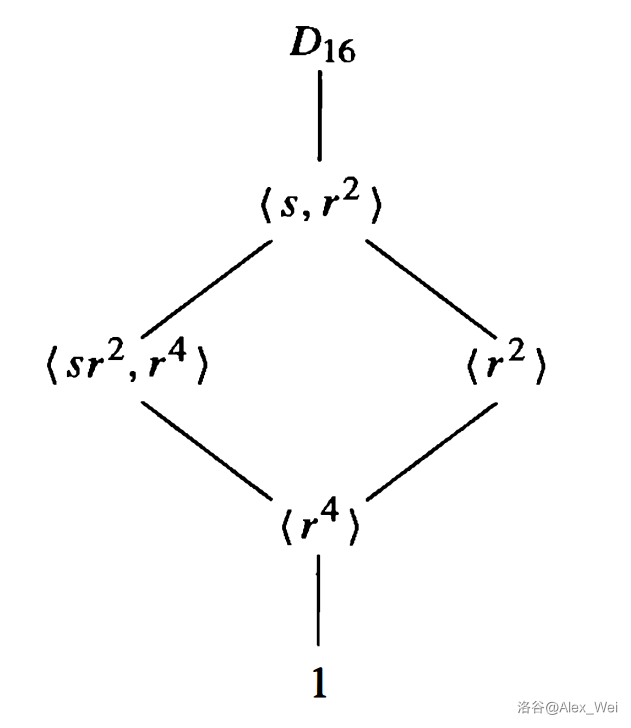
下图是
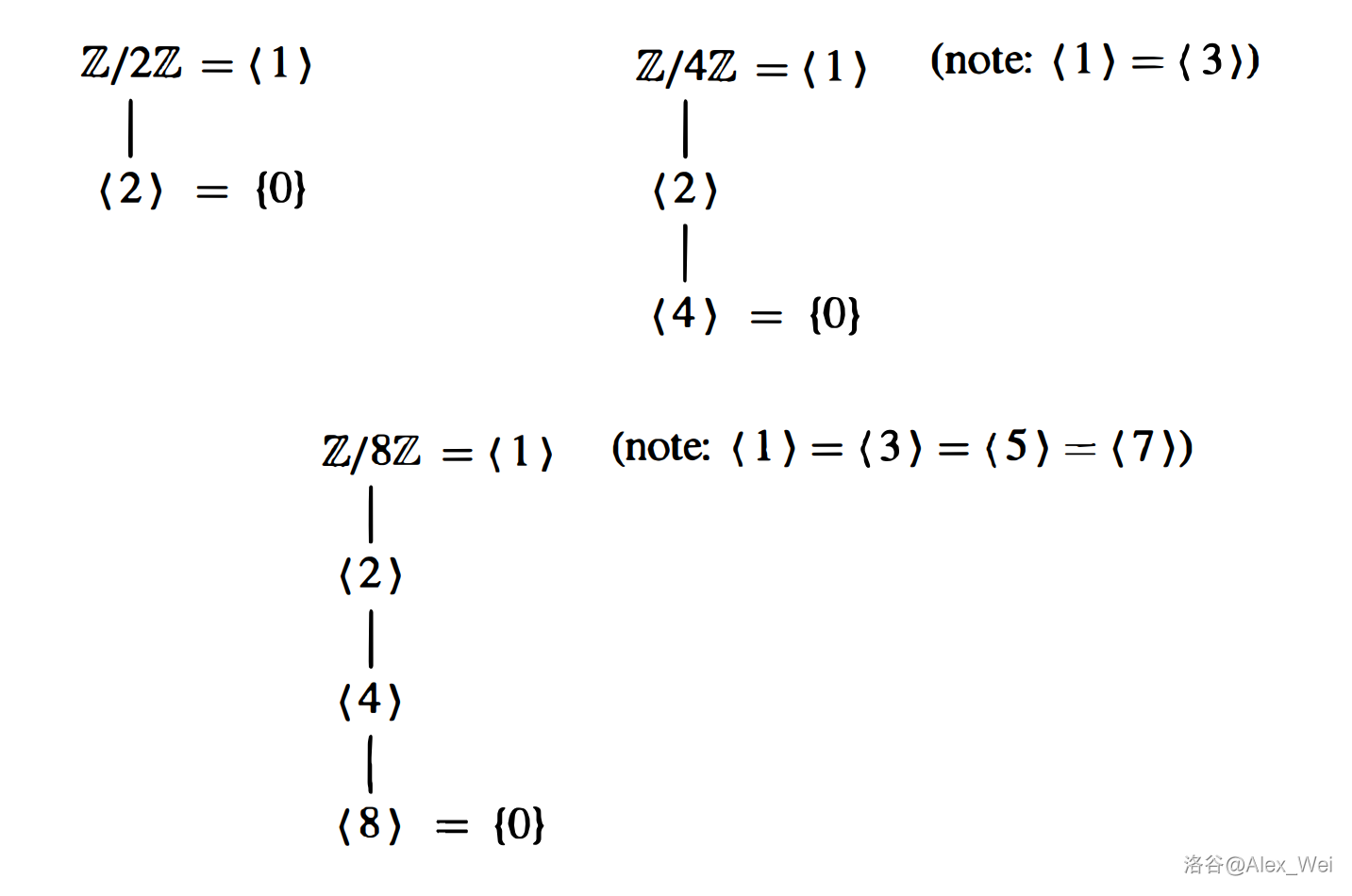
下图是
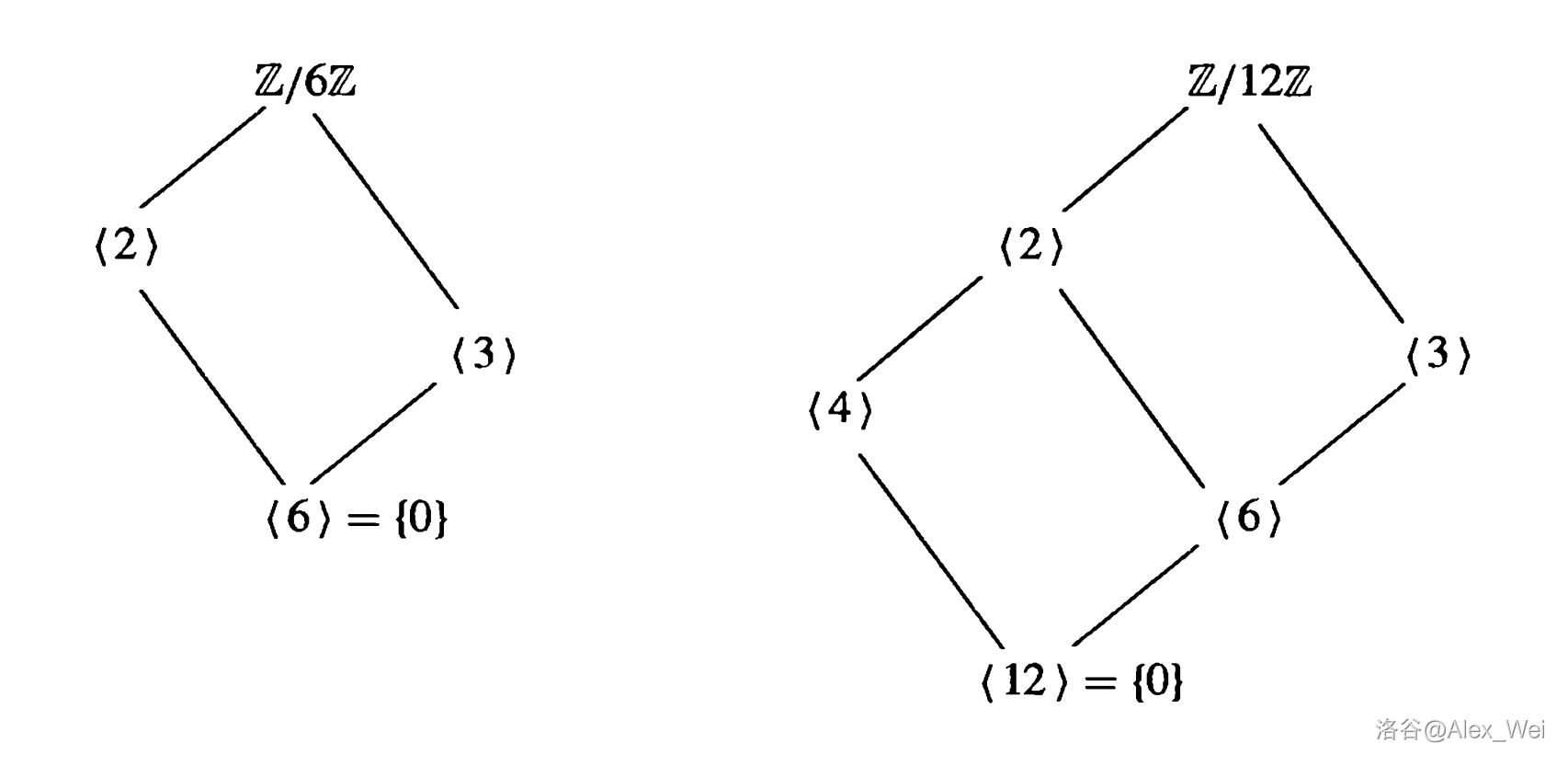
下图是
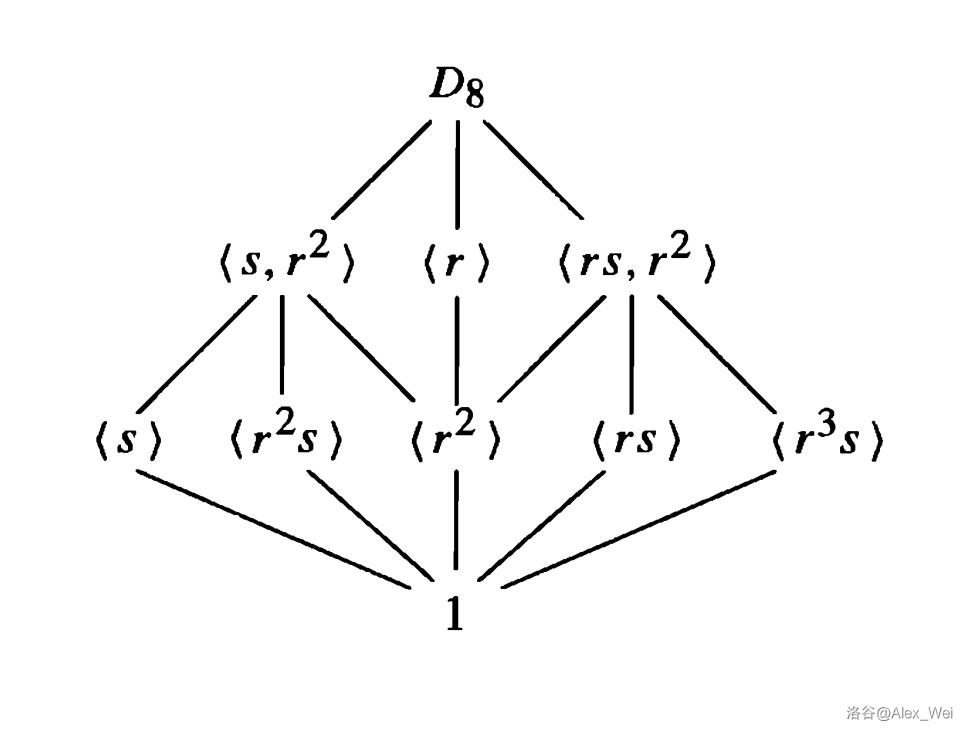
下图是
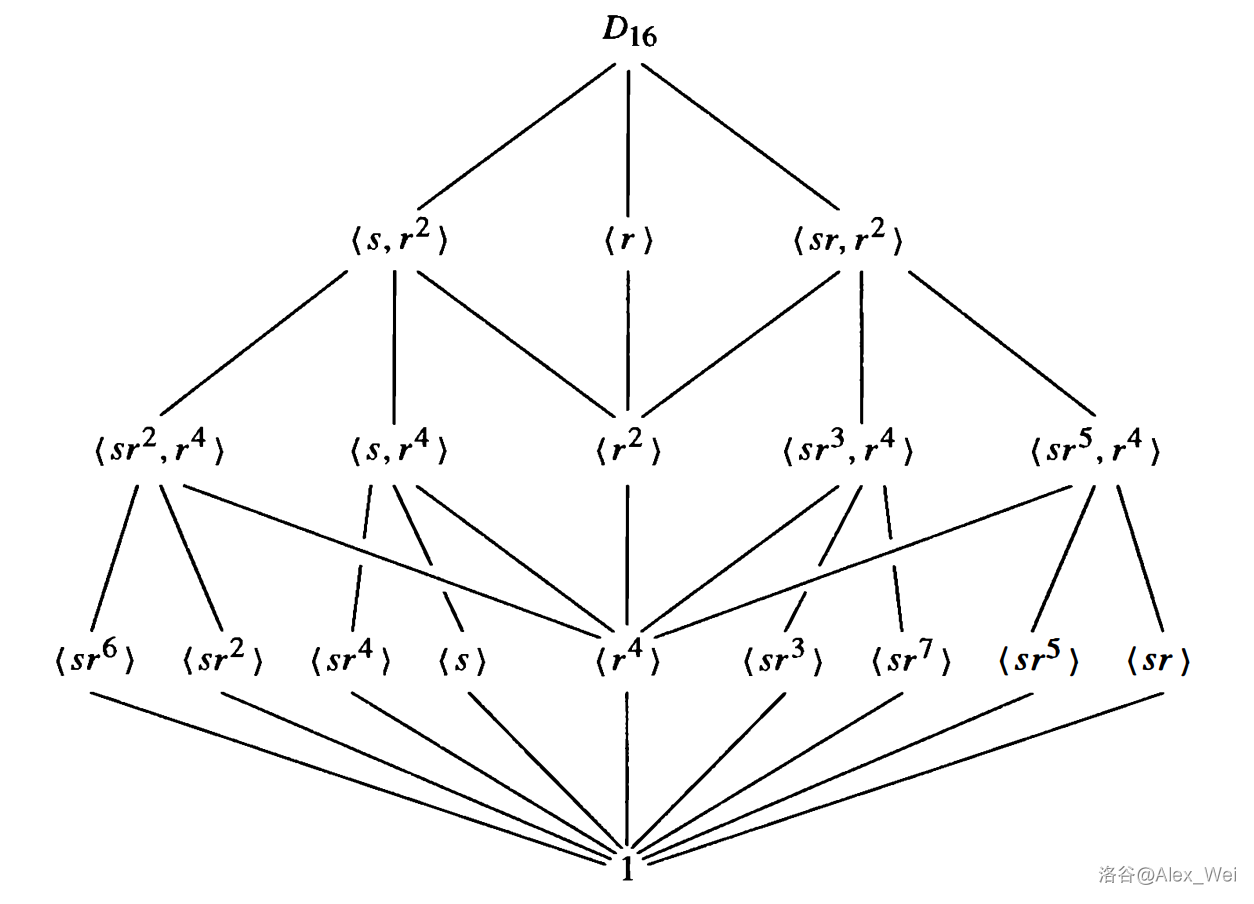
从格图可以直接读出若干子群的生成子群,也可以直接读出若干子群的交。
子格
大多数群的格比较复杂。只关心特定子群时,可以只画出相关部分,称为 子格 (Sublattice)。
有点类似 OI 中的虚树。
下图是
Chap.3 Quotient Groups and Homomorphisms
商群是另一种构造子结构的方式。商群的格在格图顶部,子群的格在格图底部。
Sec.3.1 Definition and Examples
纤维
对于映射
回忆同态的定义:
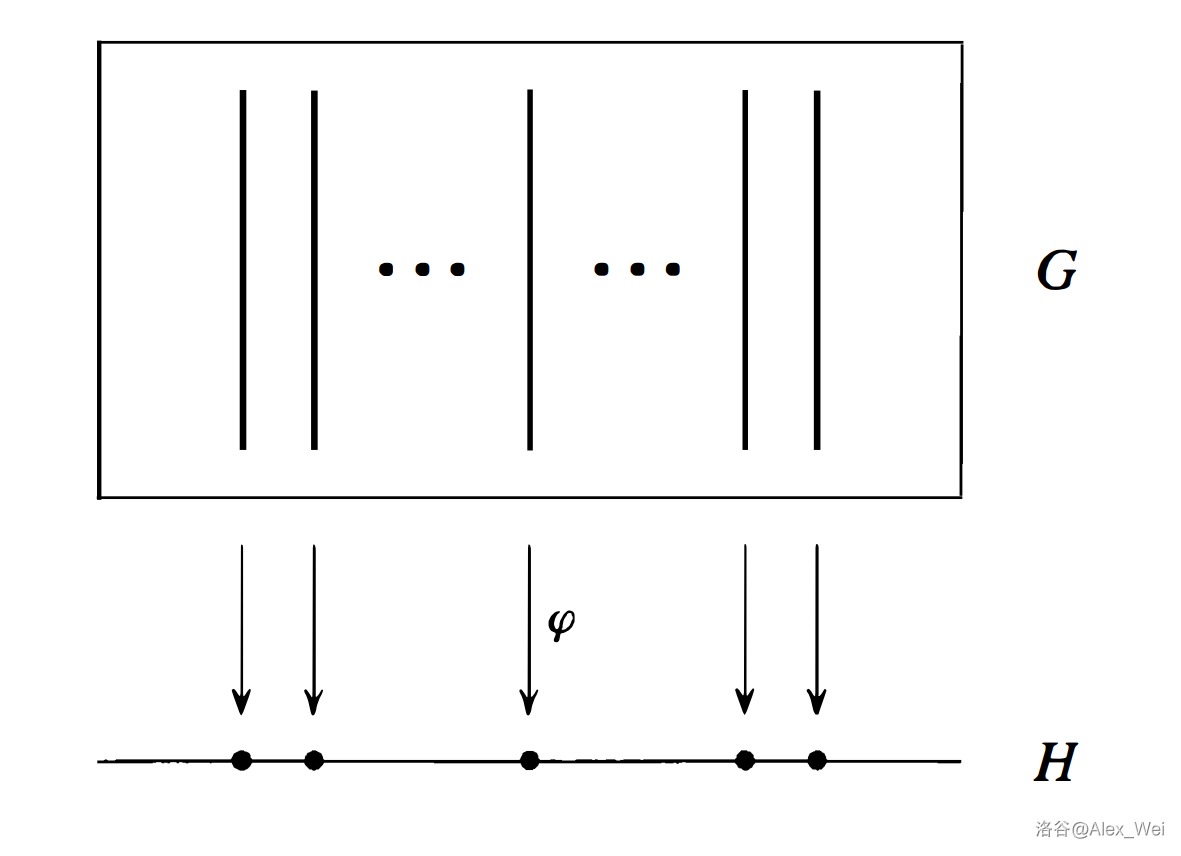
上图中,
核
对于同态
为
核就是坍缩为
的子群。
结论 3.1
令
(1)
(2)
(3)
(4)
商群
设同态
商群的元素是
记号强调了
目前,商群需要明确地表示出
结论 3.2
设同态
(1) 对任意
(2) 对任意
证明 (1):对任意
一个纤维由
所有模
为 的数可由所有 的倍数同时加上任何一个相同的模 为 的数得到。这是 。
由结论 3.2 引出以下定义。
陪集
对任意
分别为
由消去律
在左边乘上 就是左乘,对应左陪集。
结论 3.2 在纤维和左陪集(对右陪集同理)之间建立了双射,每个纤维唯一确定了一个陪集
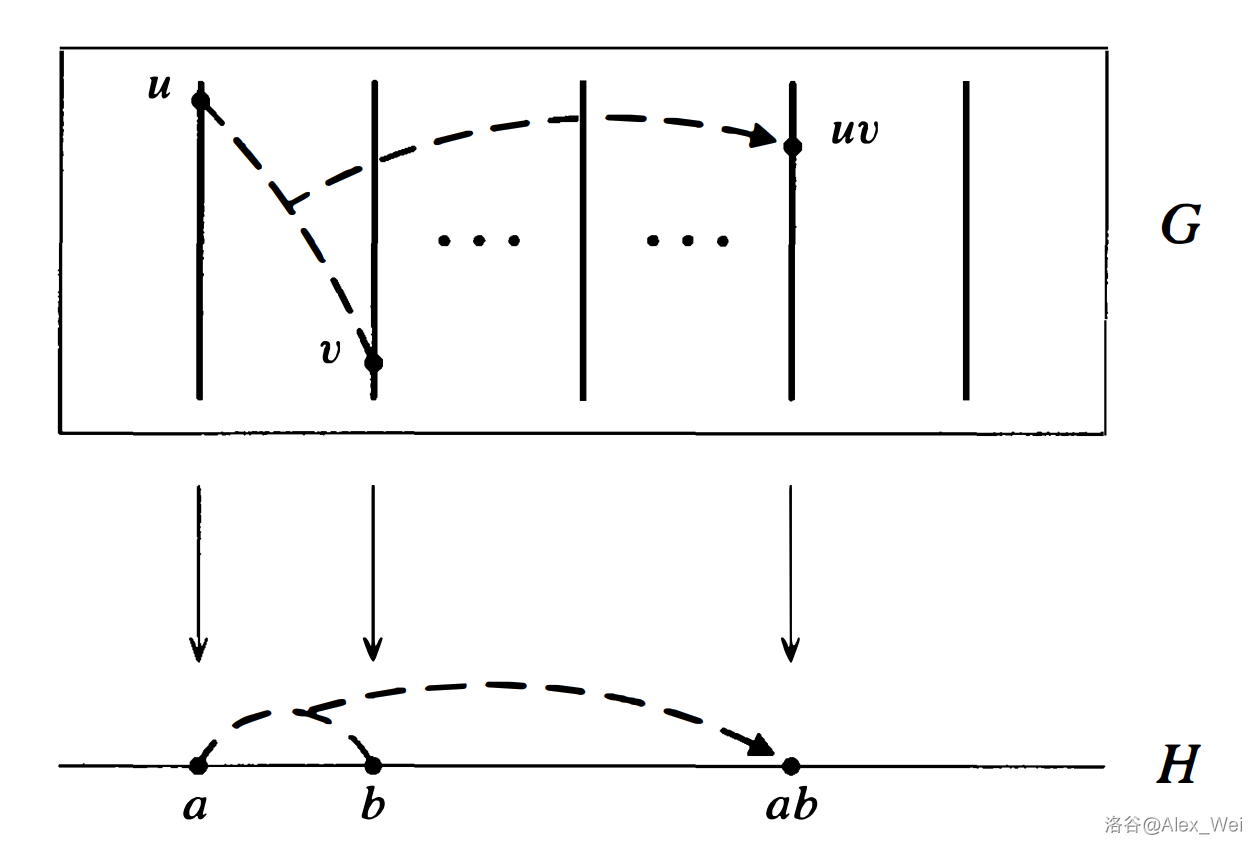
定理 3.3
设
下形成商群
证明:设
下图体现了这一过程。
若
记号
在不混淆的情况下使用
这种记号强调了左陪集
自然地,我们会思考是否对所有子群
结论 3.4
设
第一部分:因为
第二部分:由第一部分,
对于一般子群,不一定有
加上所有 的倍数等于 加上所有 的倍数,则 模 相同,即 是 的倍数,即 。 对于
(即 ),使用 可得 。
结论 3.5
设
(1)
(2) 若上述运算良定义,则
证明 (1):若运算良定义,则
其中
本质上衡量了 被 “带偏” 的程度,即先执行任意操作,再执行群里的某个操作,再执行最开始的操作的逆操作,会得到怎样的结果。如果操作依然在群里,说明这个群本身有比较好的性质。 更根本的原因是要求
,这样商群的单位元才可交换。
满足结论 3.5 的条件的子群是一类性质比较好的子群。
正规子群
称
若 \unlhd)。
总结以上所有内容,得到如下定理。
定理 3.6
以下所有论述等价:
(1)
(2)
(3) 对所有
(4) 结论 3.5 描述的运算让
(5) 对所有
特别地,
结论 3.7
证明(必要性):若
上述定义的
现在我们有不借助外部因素,仅凭
Sec.3.2 More on Cosets and Lagrange's Theorem
由结论 3.4(陪集是划分)可知
定理 3.8(Lagrange 定理)
对有限群
指标
若
记号主要用于
推论 3.9
若
由结论 2.2
推论 3.10
若
Lagrange 定理的逆命题不成立:若
定理 3.11(Cauchy 定理)
若有限群
定理 3.12(Sylow 定理)
若有限群
在下一章节中会深入研究该定理(定理 4.18)。
子群乘积
若
注意:乘积的顺序不可交换,且
结论 3.13
若
证明:因为
因为
类似
。
结论 3.14
若
注意:
若
,那么 会出现 没有的元素。注意到 ,所以若 是子群,则 。 若
,那么 ,即 关于运算封闭。
推论 3.15
若
这是结论 3.14 的简单推论:
整个小节一直在探讨左陪集的性质。对于右陪集,均有类似结论。
课上还讲了 Fermat 小定理和 Euler 定理(Exercise 3.2.16 和 3.2.22),因为太简单就略过了。
Sec.3.3 The Isomorphism Theorems
群论的重中之重,3.1 和 3.2 小节的精华。
定理 3.16(第一同构定理:The First Isomorphism Theorem)
若
同态基本定理,用于构造同态证明同构。
像同构于纤维,纤维同构于正规子群陪集集合的自然推论。
推论 3.17
若
(1)
(2)
线性代数中的
,其中 是向量空间的线性变换。
定理 3.18(第二同构定理:The Second or Diamond Isomorphism Theorem)
若
证明:因为
定理 3.19(第三同构定理:The Third Isomorphism Theorem)
若
证明:因为
商群的商群不会给出更多结构信息。
定理 3.20(第四同构定理:The Fourth or Lattice Isomorphism Theorem)
若
(1)
(2)
(3)
(4)
(5)
即
它描述了
商群的格图在顶部。
仅凭
Sec.3.4 Composition Series and The Holder Program
通过
结论 3.21
若
证明:对
这是 Cauchy 定理的弱化版本。
归纳法可行的必要条件是
简单群
若
所有简单阿贝尔群同构于
简单群在群论里的地位就像质数在代数中的地位。关于代数,有算数基本定理。群论也有类似定理。这需要以下概念。
合成列
若一列群
满足
注意:不要求
定理 3.22 (Jordan-Holder)
若有限群
(1) 存在
(2) 合成因子的可重集唯一。
Holder 计划 (The Holder Program) 是一个在同构意义下的群分类计划,分成两个部分:
(1) 将所有简单群分类。
(2) 找到所有组合简单群以得到其它群的方式。
第二部分相当困难。关于第一部分,有以下定理。
有限单群分类定理:存在
Feit-Thompson 定理:若
可解群
若存在
满足
相关定理:有限群
一个归纳法的例子:若
Sec.3.5 Transpositions and the Alternating Group
对置换群的进一步研究。OIer 会比较熟悉。
换位
长度为
将一个环表示成若干换位,则
考虑多项式
置换的奇偶性
结论 3.23
证明:根据定义展开。
结论 3.24
证明:设
交错群
由
结论 3.25
Chap.4 Group Actions
本章节进一步研究群作用在集合以及它自身上导出的性质。
Sec.4.1 Group Actions and Permutation Representation
回忆群作用和群作用的排列表示。
令
核、稳定子与忠实作用
(1) 作用的 核 (Kernel) 是以平凡的方式作用在
(2) 对
(3) 称作用是 忠实的 (Faithful),若它的核是单位元。由第一同构定理(推论 3.17),
两个元素以相同的方式作用在
有
给定
结论 4.1
对任意群
排列表示
重新定义
称特定的群作用 导出 (Afford / Induce) 了对应排列表示。
群作用的排列表示,类比线性变换的矩阵表示。
结论 4.2
令
等价关系的证明是显然的(自反性,对称性,传递性)。
证明:设包含
我们所熟知的 轨道-稳定子定理。
轨道与传递作用
令
(1) 等价类
(2) 称作用是 传递 (Transitive) 的,若仅有一个轨道。即对任意
置换群
对称群的子群称为 置换群 (Permutation Groups)。
对称群的每个元素都有唯一的环分解,其中认为一个环和它的循环移位相等。
Sec.4.2 Groups Acting on Themselves by Left Multiplication —— Cayley's Theorem
群作用于自身是一种不需要外部集合而仅由
群作用于自身
考虑作用
容易证明作用是传递且忠实的。
群作用于子群陪集集合
推广这个概念,考虑群
定理 4.3
令
(1) 作用是传递的。
(2)
(3)
(1) 和 (2) 据定义显然。
由定义
于是
假设
一个子群的所有共轭的交是这个群的最大的包含于该子群的正规子群。由正规子群的定义
容易看出这一点。
推论 4.4(Cayley 定理)
若
证明:令
定理的实用性不高,因为
太大了。
左正则表示
由
在
的左正则表示中, 是 个长度为 的环,每个环都是 的右陪集。
推论 4.5
若有限群
注意:指标为
证明:设
Sec.4.3 Groups Acting on Themselves By Conjugation —— The Class Equation
研究
共轭与共轭类
若存在
对于
的正规子群一定是若干共轭类的并。
推广至
由结论 4.2(轨道-稳定子定理),包含
结论 4.6
将结论 4.6 应用于
定理 4.7(类方程:The Class Equation)
对有限群
其中右侧的每一项都是
给出两个类方程的重要推论:
定理 4.8
若
证明:对
推论 4.9
若
接下来研究
结论 4.10
对于
证明:若
由
结论 4.11
两个
置换的环分解的环长可重集称为它的 环类型 (Cycle Type)。
由简单的组合知识,容易对给定的环类型计算其共轭类大小。
定理 4.12
Sec.4.4 Automorphisms
自同构即
自同构
共轭作用提供了最重要的自同构映射之一。
结论 4.13
设
证明:
推论 4.14
若
证明:令
只需令
即可。
推论 4.15
对任意
结合
内自同构
对
由结论 4.13,
研究
如何共轭作用于正规子群 ,只需要考察正规子群 的自同构。这对研究半直积有帮助。
特征子群
若
关于特征子群,有以下结论:
(1) 特征子群是正规子群。
(2) 若
(3) 若
特征子群是 “强正规” 子群。正规子群要求在共轭作用(部分自同构)下不变,但特征子群要求在所有自同构下不变。
结论 4.16
证明:对于
Sec.4.5 Sylow's Theorem
相当好用的定理,证明较复杂。
Sylow
设
(1) 阶为
(2) 若
(3)
Sylow 与否在于阶数是否包含了所有质因子
。
定理 4.18(Sylow 定理)
设
(1) Sylow
(2) 若
(3)
命题 3 经常用于证明
。
推论 4.20
设
(1)
(2)
(3)
(4) 设
借助 Sylow 定理可以进行简单的群分类。5.2 小节的有限生成阿贝尔群基本定理和 5.5 小节的半直积相关定理是群分类的强力工具。
4.6 小节的内容是
Chap.5 Direct and Semidirect Products and Abelian Groups
直积和半直积是两种由小群构建大群的方式,也是将大群分解为小群乘积的方式。
有限生成阿贝尔群基本定理完全分类了所有有限阿贝尔群。
Sec.5.1 Direct Products
直积
其中
类似定义无穷多个群的直积。
因为无歧义,省略所有
结论 5.1
设
结论 5.2
设
(1)
(2) 定义
(3) 使用 (1) 的表示法,对任意
很符合直觉。
推广:对
此外,直积的顺序不影响结果。
Sec.5.2 The Fundamental Theorem of Finitely Generated Abelian Groups
完整刻画了有限生成阿贝尔群的具体形态。
有限生成与自由阿贝尔群
(1) 称
(2) 对非负整数
即
元整数组。 “自由” 是范畴论的概念。
定理 5.3(有限生成阿贝尔群基本定理:Fundamental Theorem of Finitely Generated Abelian Groups)
设
(1)
(2) (1) 中的表示唯一。
根据结论 5.6 的
,如果 不是 的倍数,则存在质因子 使得 , 且 。令 , 。最终 一定是 的倍数。 对每个质因子
, 所含有 的幂次单调不增,且总和为 所含有 的幂次 。所有可能的划分方案为 的划分,且不同质因子的 独立。这引出了定理 5.5。
自由秩与不变因子
定理 5.3 中的
两个阿贝尔群同构当且仅当它们的自由秩和不变因子相等。
根据定理 5.3,给定阶
,可列举出所有 阶阿贝尔群。
推论 5.4
若
定理 5.5
设
(1)
(2) 对每个
(3) (1) 和 (2) 中的分解唯一。
特别地,
对于有限阿贝尔群,定理 5.3 和 5.5 等价。
相较于定理 5.3,定理 5.5 将阿贝尔群拆成了更基本的
的乘积。 根据定理 5.5,
阶阿贝尔群的数量为 ,其中 表示 的划分数。
初等因子
定理 5.5 中的所有
初等因子是所有 Sylow 子群的不变因子,也是 Sylow 子群的初等因子。
结论 5.6 在初等因子和不变因子之间建立了桥梁。
结论 5.6
设
(1)
(2)
证明 (1):设
秩与指数
(1) 设
(2) 设
类比线性代数的秩:
- 矩阵的秩为
即列空间是 个线性无关向量的线性组合。 - 有限阿贝尔群的秩为
即所有元素可用 个互相无关的元素的乘积表示。 自由秩对应的元素更自由:它们可以是任意幂次。不变因子
对应的元素的幂次在 范围内。
Sec.5.4 Recognizing Direct Products
将非阿贝尔群分解为群的直积。
交换子
(1) 定义
(2) 定义
(3) 定义
交换子衡量了
注意:
,于是 。
结论 5.7
设
(1)
(2)
(3) 对任意
(4)
证明 (2):
证明 (3):因为
证明 (4):若
(2):
且 说明 ,即 。 (3):令换位子群坍缩为
,则根据 以及 可知 。 (4):换位子群是最小的满足坍缩为单位元之后商群为阿贝尔群的子群。若存在交换子
没有坍缩为 ,则 在商群中不交换。相反,若所有交换子均坍缩为 (坍缩为 的子群包含换位子群),则商群任意两个元素可交换。
结论 5.8
设
定理 5.9(识别定理:Recognition Theorem)
若
证明:由
内、外直积
对
内、外直积仅在符号上有区别。
识别定理是本小节的核心,它要求
均为正规子群。若仅要求 是正规子群,欲将 分解为 的乘积,则需要下一小节的半直积工具。
Sec.5.5 Semidirect Products
半直积是直积的推广。由推论 3.15,
设
以上计算以
在有序对
根据
描述了 和 如何交换: 。从这个角度去理解, ,其中 满足 , ,对应 。
定理 5.10
设
(1)
(2)
用
(3)
(4)
(5)
证明 (5):
证明 (3):由 (5) 知
半直积
定理 5.10 定义的群 \rtimes)。不引起歧义时省略右下角标。
结论 5.11 告诉我们在什么情况下直积和半直积相等。它揭示了直积和半直积的关系:直积是一种特殊的半直积。
结论 5.11
设
(1)
(2)
(3)
由半直积的定义,(1) 的同构和 (2) 的平凡同态说明
,即 可交换。(3) 的 结合识别定理的证明也说明 可交换。 这再一次告诉我们,
本质上描述了 如何交换。 可交换则为直积,它是半直积的特例。
定理 5.12
设
正确性由本小节开头的计算验证得到。
半直积的识别定理。对应定理 5.9。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现