HMM笔记
参考资料：
1.https://www.bilibili.com/video/av24132174/?p=4
2.《数学之美》-吴军
3.《统计学习方法》-李航
HMM（Hidden Markov Model）中的Markov正是随机过程里面的马尔可夫假设的那个Markov。
一、引入
时间序列（数据）Series和集合（数据）Set是不一样的，时间序列数据中的不同两个数据点不能互换，而集合中的任意两个数据点
假设股市中的价格涨跌（观测值）背后有隐状态（牛、熊、平台），那么我们可以用Hidden Markov Model来表示这个过程。
预备知识点：
Markov假设：当前时刻t的状态qt只取决于前一时刻t-1的状态qt-1。这就是一阶马尔可夫假设。
状态转移概率矩阵（Transition Probability Matrix）A，行标是各个隐状态的可能值，列标也是，若有3个隐状态，则A是3x3阶矩阵。
观测概率矩阵（Emission Probability Matrix）B，行标是各个隐状态的可能值，列标是各个可能的观测值。注意：B不一定是矩阵形式，因为观测值不一定是discrete（离散的）。如果观测值是一个连续分布（例如高斯分布），怎么来表示这么一个观测概率矩阵呢？一定是3组（3指的是隐状态数目）高斯分布的参数μ,σ来表示的。
问题0：（模型参数）
有了A,B两个矩阵，是否足够来描述一个HMM？
问题1（求概率问题）：
比如现在告诉你连续3天股指分别是up,up,even，那么你能求出这个P(up,up,down)吗？
直接求没法求， 因为我们已经假设有隐状态了（我们就是在讨论HMM模型，而HMM就假设是存在隐状态序列的），所以应当求连续3天的隐状态和观测状态的所有组合的概率的加总。这就是联合概率分布和边缘概率分布的知识了。
快速对比：以前我们考虑二维随机变量时，举个例子：在夹娃娃机中夹娃娃时，X是夹到娃娃的结果，有成功、失败三种可能，Y是目标娃娃的大小，有大、中、小三种可能，那么怎么求3次出击的结果是（失败、失败、成功）的可能是多少？一般来说，X和Y是有关系的，就是说非独立的，因此我们得考虑3次出击的目标Y一共有几种可能，显然有3*3*3=27中可能。注意：不能说我们已经看到了3次的目标Y是多少，如果每次都看到了，那Y就不叫变量了，变量是因为它在变才叫它变量，所以我们可以理解成我们在蒙着眼睛夹娃娃，这样我们每次出击的目标Y是大、中还是小是不知道的，这才有联合概率的事儿。因此，Σ[P(y1,y2,y3,x1=失败,x2=失败,x3=成功)]（共27种情况，因为是离散，就用Σ，连续就得用积分运算了，如右图所示）才是求解P（失败、失败、成功）的正确方式。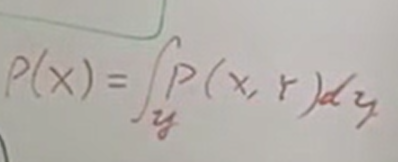
但是这个例子里面，和HMM模型不一样的地方是，3次出击是独立事件，独立事件，独立事件！也就是说，第二次的目标选的是大、中还是小和第一次的目标是大、中还是小无关！而在HMM模型里，我们考虑的对象是时间序列，而且认为隐状态之间是前后相关的。虽然上例中3次出击夹娃娃的行为也是时间序列，但是我们直观上认为这种时间序列的行为之间是互相独立的（就像中学学概率时，从黑箱里又放回地取色球一样）。
继续上面的问题1，怎么加总概率呢？根据Markov假设，我们可以得到如下：
，因此可以得到：
，我们发现，只有最右下角的P(q1)是不知道的，其余可以从A,B矩阵得到。因此我们还需要一个初始概率分布π，所以HMM模型可以由A,B,π来确定，至此回答了问题0。
问题2：HMM可以告诉你什么？你可以用HMM干什么？
HMM这一模型的最广泛、最有力的应用是在自然语言处理中，当然在任何时间序列问题中都可见其身影。HMM是如何被应用到时间序列问题中的呢？
时间序列问题，具有前后状态相关的特性，以语言识别为例，英文中的前后两个词（或中文中的前后两个字）之间是有依赖关系的，那么马尔可夫链就是描述了一个t时刻的状态变量只依赖于t-1时刻状态变量的随机过程。而隐马尔可夫（Hidden Markov Model）则是对马尔可夫链的升级。HMM应用于信号处理中的解码过程的思路是，将信号（如一段声音序列）识别为信息（如一段文本文字）。那么如何做到？HMM对马尔可夫链的扩展在于，HMM中的马尔可夫链是不可见的，而传统随机过程中的各个状态显然是可见的；而与不可见的隐状态序列相关的有一个可见的观测序列，观测序列每个观测值yt仅取决于当前时刻的隐含状态qt。
那么识别一段语音为文字的问题，就相当于信号处理中的解码问题， 将声音序列看作可观测序列Y:y1,y2,...,yT,将文字序列看作隐状态序列Q:q1,q2,...,qT.
而HMM所依赖的马尔可夫假设、观测独立性假设，使得求取某个特定的状态序列Q和观测序列Y同时出现的概率分解为：
P(q1,q2,...,qT,y1,y2,...,yT)=ΠtP(qt|qt-1)·P(yt|qt)，................(1)
而在通信的解码问题中，我们已知观测信号y1,y2,...,yT的情况下，要求令条件概率P(q1,q2,...,qT|y1,y2,...,yT)达到最大值的那个源信息串q1,q2,...,qT，这可以等价为求最大的P(q1,q2,...,qT,y1,y2,...,yT)=P(y1,y2,...,yT|q1,q2,...,qT)·P(q1,q2,...,qT)................(2).对比(1)、(2)两式，可以很显然地看到，如果将解码问题与HMM模型中的观测序列、状态序列对应起来，那么采用HMM模型可以描述解码问题，即HMM的两个假设可以将（2）的右式用（1）的右式来表示出来。
问题3：HMM可以告诉你什么？你可以用HMM干什么？
HMM的三种问题：
1.已知模型λ(A,B,π)，求解P(Y)；
2.已知模型λ(A,B,π)和特定的观测序列Y，求生成Y的最可能隐藏状态序列Y；
3.给定足够的观测数据Y，如何训练出一个模型？即求取λ(A,B,π)。
一般来说，第1类和第3类问题比较多，求第1类也得先求出第3类问题后才能进行。
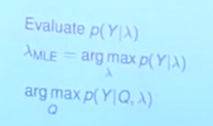此图中3个问题分别为1.概率计算；2.模型学习；3.模型预测；
求取第3类问题，即模型训练问题，可以通过鲍姆-韦尔奇算法（Baum-Welch Algorithm）来训练。
E-M算法：
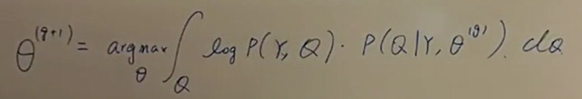
将被积分的后面一项条件概率P(Q|Y)乘以常数项P(Y)后，得到如下形式：
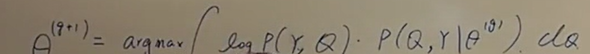
两式之间的关系如下：
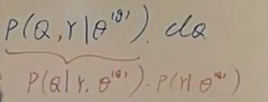
将离散序列Q展开：
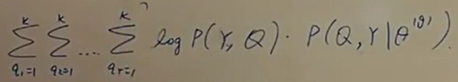
应用拉格朗日法求解，先求π。
上图右下角的结论：
可以通过Forward-Backward Formula计算出来。
求a
求b
鲍姆-韦尔奇算法的思想是这样的：（取自资料2）
首先找到一组能够产生输出序列Y的模型参数。现在，有了这样一个初始的模型之后，我们称为λ(g)，需要在此基础上找到一个更好的模型。假定解决了第一个问题和第二个问题，不但可以算出这个模型产生观测序列Y的概率P(Y|λ(g))，而且能够找到这个模型产生Y的所有可能路径（一般所有的可能隐状态序列数目就是kT，因为基本上每个隐状态都可以产生任意观测值，比如盲人预测天气情况的例子）以及这些路径的概率（这些概率的和为1，路径概率分布的不同源于模型的差异）。这些可能的路径，实际上记录了每个状态经历了多少次，到达了哪些状态，输出了哪些符号，因此可以将它们看做是“标注的训练数据”，并且根据公式：
计算出一组新的模型参数λ(g+1),从λ(g)到λ(g+1)的过程称为一次迭代。可以证明P(Y|λ(g+1))>P(Y|λ(g))。
鲍姆-韦尔奇算法的每一次迭代都是不断地估计新的模型参数，使得输出的概率（我们的目标函数）达到最大化（Maximization），因此这个过程被称为期望值最大化(Expecation-Maximization)，简称EM过程。
求取第1类问题相对简单，采用的是Forward-Backward算法。首先，我们可以将P(Y|λ)按如下展开，完全由A,B,π计算得到，但是显然这样的计算量很大，因为展开后的项特别多。如下图所示。
Forward-Backward算法先定义了α项和β项，这存粹是个定义，没有数学的运算在里面。如下图所示。
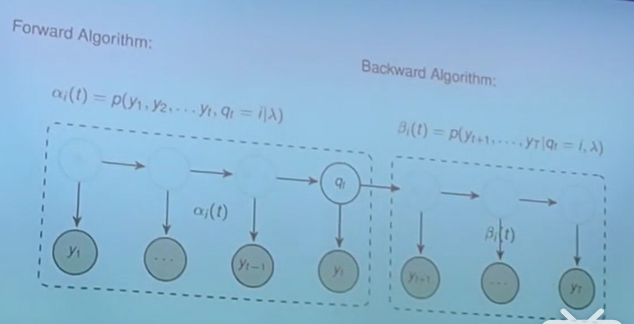
有了α项和β项，如何能够帮助简化原先的巨大的计算量呢？先来按照它们的定义，试着写一些α项。图中在计算αj(2)时，硬是将q1(即t=1时刻的隐状态)这个变量塞了进去，但是同时得把它积分积掉，以保持等式成立（下图中最后一个等式中的Σ就是这个作用）。
展开后，发现第2项可以包含第1项，如下：
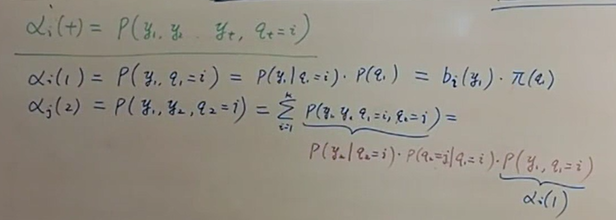
再由于第1项跟i没有关系，可以提取到Σ的外面。如下图所示：
注意最后一行是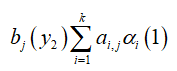
，即
之间是有关系的，后一时刻的前向概率α可以由前一时刻的前向概率α表示。我们可以很容易写出如下的式子：
注意到，在计算
时我们只要计算一项就行了，没有加总符号Σ；而在计算
中的任意一个前向概率时，需要k个项的加总。因此总共需要(T-1)*k项即可，这样的计算量远比一开始的kT次加法来的小。
问题：计算每一时刻的前向概率α，为了干嘛？为了计算后一时刻的α。那最后t=T时刻的前向概率
算出来了，它能够干嘛？根据定义，可以发现只要将
按j从1到k积分就得到了我们的目标P(Y|λ)。
如此，我们用了好的方法后（递归的思想），节省了很多的计算量，看来费劲脑子去思考方法（算法）是有很大的益处的！
后向概率β是从t=T开始往前算到t=1的，具体不展开说。（截屏记录一下）
求取第2类问题，可以用著名的维特比算法解决。（参考资料3，《统计学习方法》-李航）
维特比算法实际是用动态规划解隐马尔可夫模型预测问题，即用动态规划求概率最大路径（最优路径），这时一条路径对应着一个状态序列。
下面给出了维特比算法的流程：
