决策树&随机森林
参考链接:
https://www.bilibili.com/video/av26086646/?p=8
《统计学习方法》
一、决策树算法:
1.训练阶段(决策树学习),也就是说:怎么样构造出来这棵树?
2.剪枝阶段。
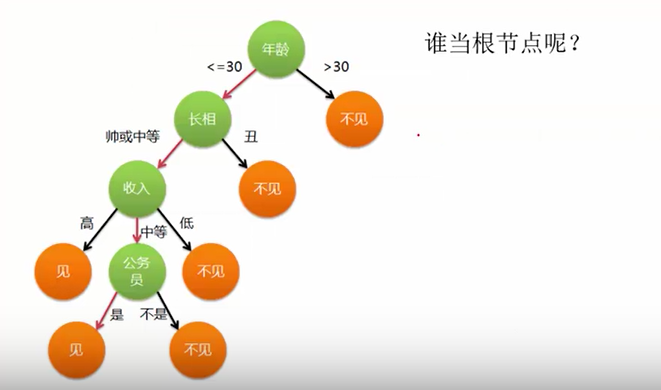
问题1:构造决策树,谁当根节点?例:相亲时为啥选年龄作为根节点?
H(X)为事件发生的不确定性。
事件X,Y相互独立,概率P(X),P(Y)。认为:P(几率越大)->H(X)越小,如今天正常上课。P(几率越小)->H(X)越大,如今天翻车了。
熵是表示随机变量不确定性的度量。熵越大,不确定性越大,越混乱。
设X是一个取有限个值的离散随机变量,其概率分布为:P(X=xi)=pi, i=1,2,...,n,则随机变量X的熵定义为:

由定义可知,熵只依赖于X的分布,而与X的取值无关,所以也可将X的熵记做H(p)。![]()
例2:对于两个集合A,B来说,如果A比较混乱,B内部比较单一纯净,那么集合A的熵更大。
思想:构造决策树,随着深度的增加,节点的熵迅速降低。熵降低的速度越快越好,迅速地构建出决策树。\
案例(根据天气判断是否打篮球):
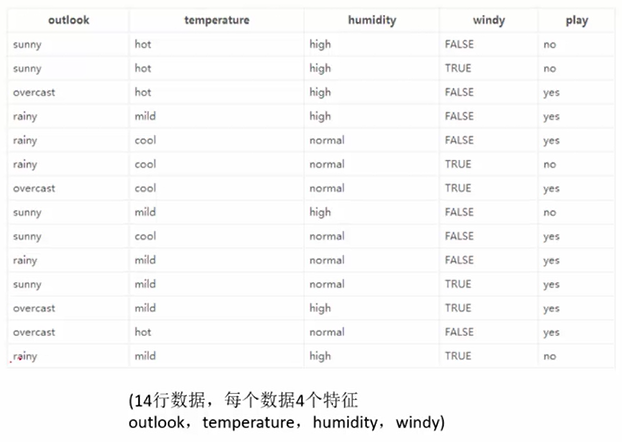
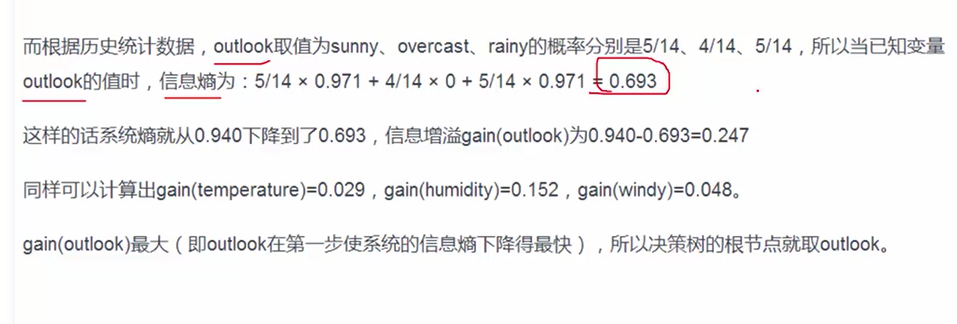
1.先计算原始数据的熵,为0.940.

2.再计算按照4中划分方式得到的熵(确切地说,是条件熵,H(Y|X)),以及信息增益gain。比如基于Outlook划分时,熵为0.693,信息增益=0.940-0.693=0.247.算出四种划分的信息增益,越大越好,得出gain(outlook)最大的结论。


问题2:怎么样衡量最终决策树好不好,衡量划分的效果呢?机器学习算法中,都有一个目标函数。
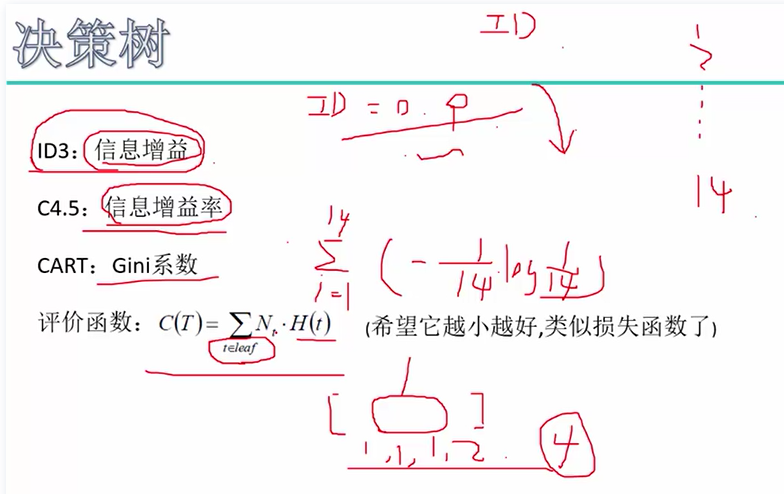
我们希望最后的C(T)越小越好,越小说明分类效果还不错。
问题3:若属性值是连续的怎么办?离散化,用阈值和不等式来离散化。如下例子所示:
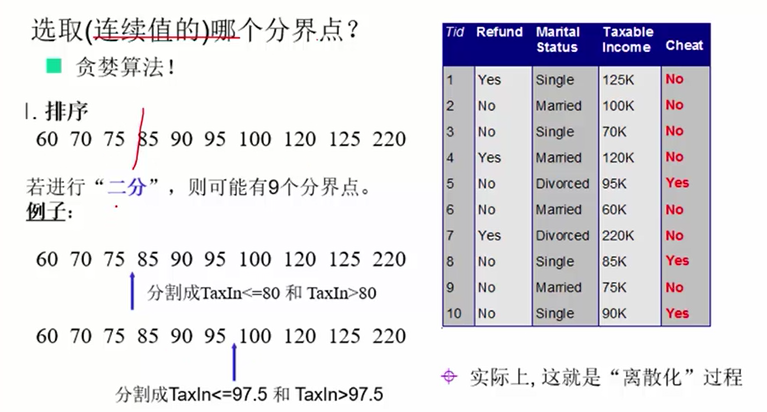
思想:我们希望得到一颗高度最矮的决策树。
切得太碎,太细,容易出现过拟合。即树不能太高,因为树越高说明分支越多。因此,思考怎么样使得建立的决策树别把所有的叶子节点都只包含一个样本。
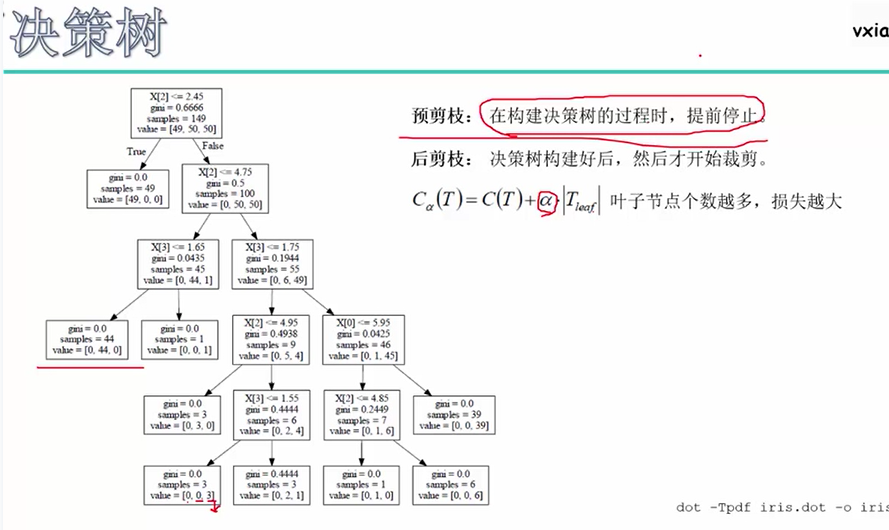
预剪枝:比如d=3,当高度超过3时停止分裂;比如min_sample=50,也就是说节点所含的样本数低于50个时,停止分裂。
后剪枝:C(T)为原来的评价函数,新的评价函数Cα(T)考虑了叶子节点的个数。
二、随机森林算法
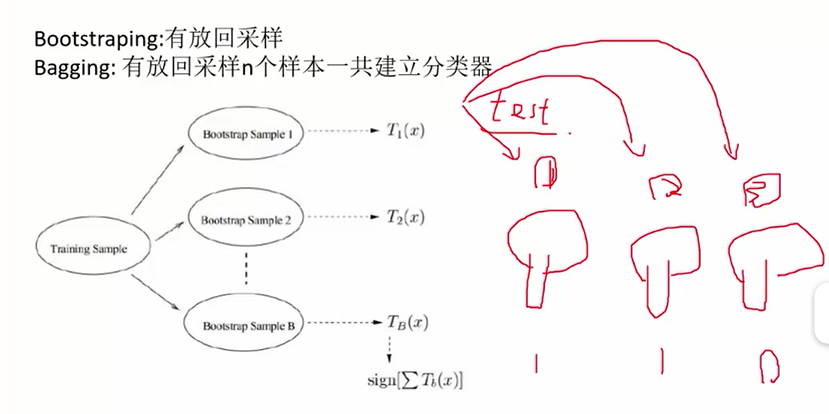
随机森林:构造出多棵决策树,然后分类问题取众数(或者其它取法),回归问题取平均数。用这一片决策树进行预测。
随机森林:1.建立每一棵树的时候,都随机选择其中一部分样本(有放回地采样!),这样有时候可以避免掉不好的样本点,从而构造出比较好的树。
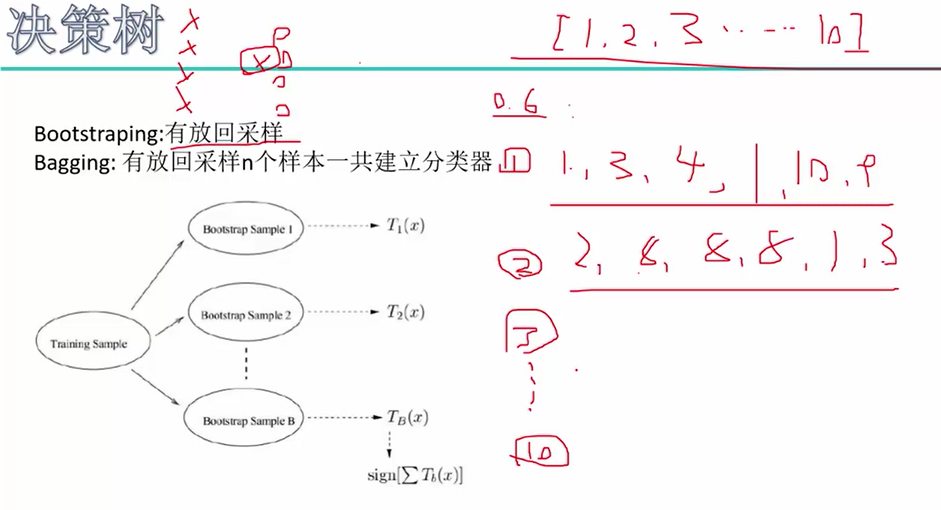
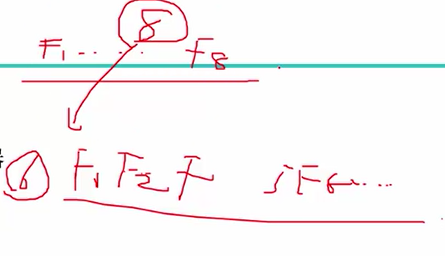
2.构建每一棵树时,随机选择一部分特征(比如8个特征里面取6个)。两重随机性,第一重是样本的随机性,第二重是特征的随机性。
三、python实战——鸢尾花分类
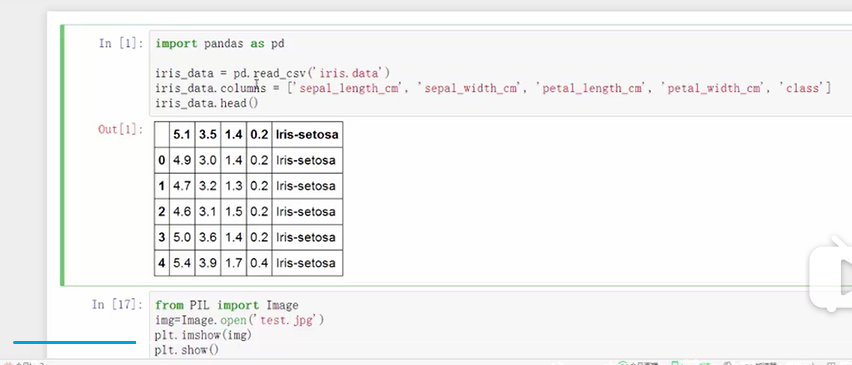
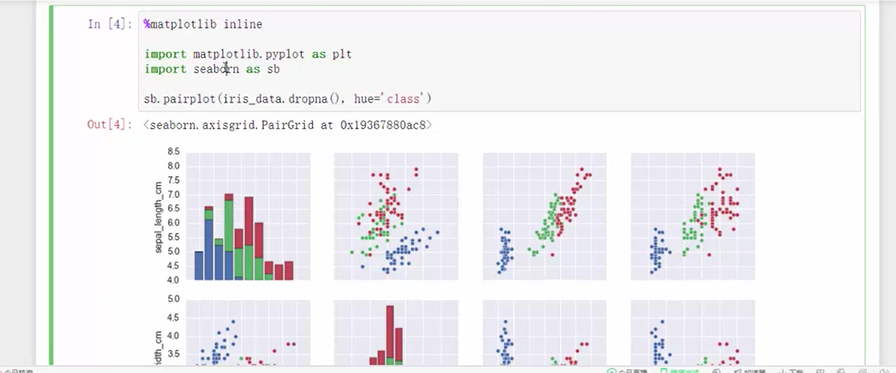
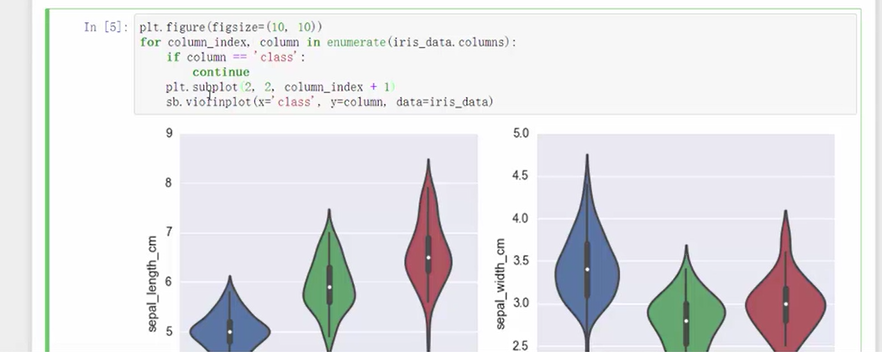
代码: