【POJ 1737】Connected Graph
Connected Graph
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 3010 | Accepted: 1481 |
Description
An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.
For example,there are 4 different connected undirected graphs with 3 vertices.
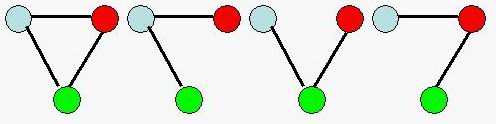
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.
For example,there are 4 different connected undirected graphs with 3 vertices.

Input
The input contains several test cases. Each test case contains an integer n, denoting the number of vertices. You may assume that 1<=n<=50. The last test case is followed by one zero.
Output
For each test case output the answer on a single line.
Sample Input
1 2 3 4 0
Sample Output
1 1 4 38
Source
教主的题目。
第一题应该是相对其它题来说较简单的了吧。
其实在刘汝佳的书上有提到过。
设f(n)为答案,g(n)则为有n个顶点的不连通图的个数,h(n)是总方案数。
很明显,对于h(n)我们可以直接求出,因为每一条边有两种情况,一共有n*(n-1)/2条边,所以 f(n) + g(n) = h(n) = 2n*(n-1)/2。
然后我们要求出g(n)是多少。选择一个点作为中心,假设是V1,那么和V1在一起成为一个连通块的方案数是 sum{C(n-1,i-1)*f(i)*h(n-i)},这个式子表示n个点除了V1外的点,要拿出i-1个顶点和V1凑成i个点的连通图的方案数,当然,根据乘法原理,除了这i个点以外的n-i个点有h(n-i)种情况,所以要两个结果相乘。
最坑爹的是用十进制的高精度会超时,我们要用万进制来节省时间。这个算法的时间复杂度是O(N2)(除高精度外)。
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; struct BigInt { static const int BASE = 10000; int s[1000]; int len; BigInt() { memset(s, 0, sizeof(s)); len = 0; s[len++] = 0; } BigInt operator = (const int &b) { memset(s, 0, sizeof(s)); len = 0; s[len++] = b; int i = 0; while (s[i] > BASE) { s[len++] = (s[i] / BASE); s[i] %= BASE; } return (*this); } BigInt operator + (const int &b) { s[0] += b; for (int i = 1; i < len; ++i) { s[i] += s[i - 1] / BASE; s[i - 1] %= BASE; } if (s[len - 1] > BASE) { s[len] = s[len - 1] / BASE; s[len - 1] %= BASE; len++; } return (*this); } BigInt operator + (const BigInt &b) const { BigInt c; c.len = max(b.len, len); for (int i = 0; i < c.len; ++i) { c.s[i] += s[i] + b.s[i]; c.s[i + 1] += c.s[i] / BASE; c.s[i] %= BASE; } while (c.s[c.len]) { c.s[c.len + 1] = c.s[c.len] / BASE; c.s[c.len++] %= BASE; } return c; } BigInt operator * (int x) { for (int i = 0; i < len; ++i) s[i] *= x; for (int i = 0; i < len; ++i) { s[i + 1] += s[i] / BASE; s[i] %= BASE; } while (s[len]) { s[len + 1] = s[len] / BASE; s[len++] %= BASE; } return (*this); } BigInt operator * (const BigInt &b) const { BigInt c; int x, m; for (int i = 0; i < b.len; ++i) { x = 0; for (int j = 0; j < len; ++j) { c.s[i + j] += x + b.s[i] * s[j]; x = c.s[i + j] / BASE; c.s[i + j] %= BASE; } c.s[i + len] += x; } c.len = b.len + len; while (c.len > 1 && c.s[c.len - 1] == 0) c.len--; while (c.s[c.len]) { c.s[c.len + 1] = c.s[c.len] / BASE; c.s[c.len] %= BASE; } return c; } BigInt operator - (const BigInt &b) { BigInt c; memcpy(c.s, s, sizeof(s)); c.len = len; for (int i = 0; i < b.len; ++i) { c.s[i] = c.s[i] - b.s[i]; if (c.s[i] < 0) { c.s[i] = BASE + c.s[i]; c.s[i + 1]--; } } while (c.len > 1 && c.s[c.len - 1] == 0) c.len--; return c; } BigInt operator / (const int &b) const { BigInt c; c = 0; int x = 0; for (int i = len - 1; i >= 0; --i) { x = x * BASE + s[i]; if (x >= b) { c = c * BASE + x / b; x %= b; } else c = c * BASE; } return c; } }; const int MAXN = 55; BigInt h[MAXN], g[MAXN], f[MAXN]; int n; BigInt C(int m, int k) { BigInt ans; ans = 1; for (int i = m - k + 1; i <= m; ++i) ans = ans * i; for (int i = 1; i <= k; ++i) ans = ans / i; return ans; } int main() { h[0] = 1; h[1] = 1; f[1] = 1; g[1] = 0; for (int i = 2; i <= 50; ++i) { h[i] = 1; for (int j = 0; j < i * (i - 1) / 2; ++j) h[i] = h[i] * 2; for (int j = 1; j < i; ++j) g[i] = g[i] + (C(i - 1, j - 1) * f[j] * h[i - j]); f[i] = h[i] - g[i]; } while (scanf("%d", &n) == 1 && n) { printf("%d", f[n].s[f[n].len - 1]); for (int i = f[n].len - 2; i >= 0; --i) printf("%04d", f[n].s[i]); printf("\n"); } return 0; }



