计算系数

题目描述

给定一个多项式(by+ax)^k，请求出多项式展开后x^n * y^m 项的系数。

输入

共一行，包含5 个整数，分别为 a ，b ，k ，n ，m，每两个整数之间用一个空格隔开。0≤k≤1000, 0≤n,m≤k 且 n+m=k, 0≤a,b≤100,000

输出

输出共1 行，包含一个整数，表示所求的系数，这个系数可能很大，输出对10007 取模后的结果。

样例输入

1 1 3 1 2

样例输出

3

二项式展开式（牛顿二项式定理）：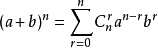

 

求逆元：费马小定理、拓展欧几里得

 

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int mod=10007;

long long quickpow(long long a,long long b)
{
    if(b<0) return 0;
    long long ret=1;
    a%=mod;
    while(b)
    {
        if(b&1) ret =(ret*a)%mod;
        b>>=1;
        a = (a*a)%mod;
    }
    return ret;
}

long long inv(long long a)
{
    return quickpow(a,mod-2);
}

int main()
{
    int a,b,k,n,m;
    cin>>a>>b>>k>>n>>m;
    long long x1=1,x2=1;
    int temp=n;
    while(temp--)
    {
        x1 = ((x1%mod)*(a%mod))%mod;
    }
    temp = k-n;
    while(temp--)
    {
        x2 = ((x2%mod)*(b%mod))%mod;
    }
    long long y1=1,y2=1;
    for(int i=k;i>k-n;i--)
    {
        y1 =((y1%mod)*(i%mod))%mod;
    }
    for(int i=1;i<=n;i++)
    {
        y2 =((y2%mod)*(i%mod))%mod;
    }
    y2 = inv(y2);
    long long ans;
    long long y=y1*y2;
    if(n==0||n==k) y=1;
    ans = (((x1*x2)%mod)*(y%mod))%mod;
    cout<<ans<<endl;
    return 0;
}