[译]《数学:更好的解释》之培养数学直觉

Developing Your Intuition For Math

Our initial exposure to an idea shapes our intuition. And our intuition impacts how much we enjoy a subject. What do I mean?

Suppose we want to define a “cat”:

• Caveman definition: A furry animal with claws, teeth, a tail, 4 legs, that purrs when happy and hisses when angry…
• Evolutionary definition: Mammalian descendants of a certain species (F. catus), sharing certain characteristics…
• Modern definition: You call those definitions? Cats are animals sharing the following DNA: ACATACATACATACAT…

(Illustration courtesy Common Craft)

The modern definition is precise, sure. But is it the best? Is it what you’d teach a child learning the word? Does it give better insight into the “catness” of the animal? Not really. The modern definition is useful, but after getting an understanding of what a cat is. It shouldn’t be our starting point.

Unfortunately, math understanding seems to follow the DNA pattern. We’re taught the modern, rigorous definition and not the insights that led up to it. We’re left with arcane formulas (DNA) but little understanding of what the idea is.

Let’s approach ideas from a different angle. I imagine a circle: the center is the idea you’re studying, and along the outside are the facts describing it. We start in one corner, with one fact or insight, and work our way around to develop our understanding. Cats have common physical traits leads to Cats have a common ancestor leads to A species can be identified by certain portions of DNA. Aha! I can see how the modern definition evolved from the caveman one.

But not all starting points are equal. The right perspective makes math click — and the mathematical “cavemen” who first found an idea often had an enlightening viewpoint. Let’s learn how to build our intuition.

What is a Circle?

Time for a math example: How do you define a circle?

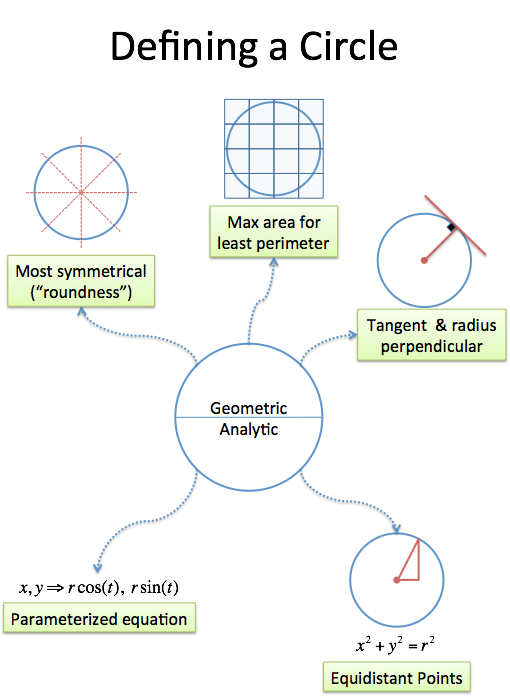
There are seemingly countless definitions. Here’s a few:

• The most symmetric 2-d shape possible
• The shape that gets the most area for the least perimeter (see the isoperimeter property)
• All points in a plane the same distance from a given point (drawn with a compass, or a pencil on a string)
• The points (x,y) in the equation x² + y² = r² (analytic version of the geometric definition above)
• The points in the equation r * cos(t), r * sin(t), for all t (really analytic version)
• The shape whose tangent line is always perpendicular to the position vector (physical interpretation)

The list goes on, but here’s the key: the facts all describe the same idea! It’s like saying 1, one, uno, eins, “the solution to 2x + 3 = 5″ or “the number of noses on your face” — just different names for the idea of “unity”.

But these initial descriptions are important — they shape our intuition. Because we see circles in the real world before the classroom, we understand their “roundness”. No matter what fancy equation we see (x² + y² = r²), we know deep inside that a circle is “round”. If we graphed that equation and it appeared square, or lopsided, we’d know there was a mistake.

As children, we learn the “caveman” definition of a circle (a really round thing), which gives us a comfortable intuition. We can see that every point on our “round thing” is the same distance from the center. x² + y² = r² is the analytic way of expressing that fact, using the Pythagorean theorem for distance. We started in one corner, with our intuition, and worked our way around to the formal definition.

Other ideas aren’t so lucky. Do we instinctively see the growth of e, or is it an abstract definition? Do we realize the rotation of i, or is it an artificial, useless idea?

A Strategy For Developing Insight

I still have to remind myself about the deeper meaning of e and i — which seems as absurd as “remembering” that a circle is round or what a cat looks like! It should be the natural insight we start with.

Missing the big picture drives me crazy: math is about ideas — formulas are just a way to express them. Once the central concept is clear, the equations snap into place. Here’s a strategy that has helped me:

• Step 1: Find the central theme of a math concept. This can be difficult, but try starting with its history. Where was the idea first used? What was the discoverer doing? This use may be different from our modern interpretation and application.
• Step 2: Explain a property/fact using the theme. Use the theme to make an analogy to the formal definition. If you’re lucky, you can translate the math equation (x² + y² = r²) into a plain-english statement (“All points the same distance from the center”).
• Step 3: Explore related properties using the same theme. Once you have an analogy or interpretation that works, see if it applies to other properties. Sometimes it will, sometimes it won’t (and you’ll need a new insight), but you’d be surprised what you can discover.

Let’s try it out.

A Real Example: Understanding e

Understanding the number e has been a major battle. e appears all of science, and has numerous definitions, yet rarely clicks in a natural way. Let’s build some insight around this idea. The following section will have several equations, which are simply ways to describe ideas. Even if the equation is gibberish, there’s a plain-english idea behind it.

Here’s a few popular definitions of e:

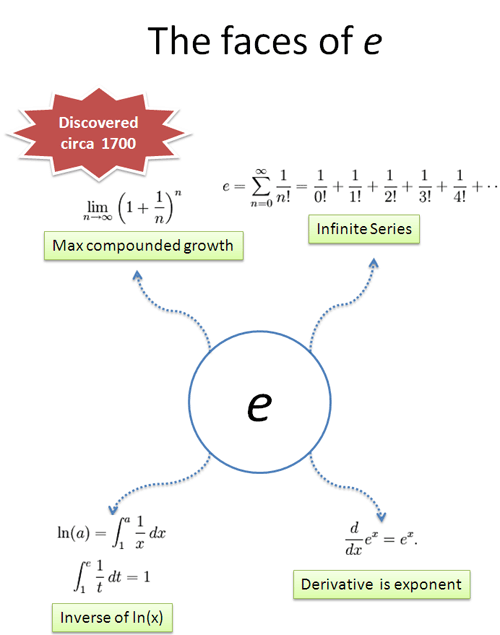
The first step is to find a theme. Looking at e’s history, it seems it has something to do with growth or interest rates. e was discovered when performing business calculations (not abstract mathematical conjectures) so “interest” (growth) is a possible theme.

Let’s look at the first definition, in the upper left. The key jump, for me, was to realize how much this looked like the formula for compound interest. In fact, it is the interest formula when you compound 100% interest for 1 unit of time, compounding as fast as possible.

• Definition 1: Define e as 100% compound growth at the smallest increment possible.

The article on e describes this interpretation.

Let’s look at the second definition: an infinite series of terms, getting smaller and smaller. What could this be?

After noodling this over using the theme of “interest” we see this definitions shows the components of compound interest. Now, insights don’t come instantly — this insight might strike after brainstorming “What could 1 + 1 + 1/2 + 1/6 + …” represent when talking about growth?”

Well, the first term (1 = 1/0!, remembering that 0! is 1) is your principal, the original amount. The next term (1 = 1/1!) is the “direct” interest you earned — 100% of 1. The next term (0.5 = 1/2!) is the amount of money your interest made (“2nd level interest”). The following term (.1666 = 1/3!) is your “3rd-level interest” — how much money your interest’s interest earned!

Money earns money, which earns money, which earns money, and so on — the sequence separates out these contributions (read the article on e to see how Mr. Blue, Mr. Green & Mr. Red grow independently). There’s much more to say, but that’s the “growth-focused” understanding of that idea.

• Definition 2: Define e by the contributions each piece of interest makes

Neato.

Now to the 3rd, and shortest definition. What does it mean? Instead of thinking “derivative” (which turns your brain into equation-crunching mode), think about what it means. The feeling of the equation. Make it your friend.

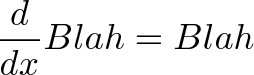
It’s the calculus way of saying “Your rate of growth is equal to your current amount”. Well, growing at your current amount would be a 100% interest rate, right? And by always growing it means you are always calculating interest — it’s another way of describing continuously compound interest!

• Definition 3: Define e as a function that always grows at 100% of your current value

Nice — e is the number where you’re always growing by exactly your current amount (100%), not 1% or 200%.

Time for the last definition — it’s a tricky one. Here’s my interpretation: Instead of describing how much you grew, why not say how long it took?

If you’re at 1 and growing at 100%, it takes 1 unit of time to get from 1 to 2. But once you’re at 2, and growing 100%, it means you’re growing at 2 units per unit time! So it only takes 1/2 unit of time to go from 2 to 3. Going from 3 to 4 only takes 1/3 unit of time, and so on.

The time needed to grow from 1 to A is the time from 1 to 2, 2 to 3, 3 to 4… and so on, until you get to A. The first definition defines the natural log (ln) as shorthand for this “time to grow” computation.

ln(a) is simply the time to grow from 1 to a. We then say that “e” is the number that takes exactly 1 unit of time to grow to. Said another way, e is is the amount of growth after waiting exactly 1 unit of time!

• Definition 4: Define the time needed to grow continuously from 1 to a as ln(a). e is the amount of growth you have after 1 unit of time.

Whablamo! These are four different ways to describe the mysterious e. Once we have the core idea (“e is about 100% continuous growth”), the crazy equations snap into place — it’s possible to translate calculus into English. Math is about ideas!

What’s the Moral?

In math class, we often start with the last, most complex idea. It’s no wonder we’re confused — we’re showing DNA and expecting students to see the cat.

I’ve learned a few lessons from this approach, and it underlies how I understand and explain math:

• Search for insights and apply them. That first intuitive insight can help everything else snap into place. Start with a definition that makes sense and “walk around the circle” to find others.
• Develop mental toughness. Banging your head against an idea is no fun. If it doesn’t click, come at it from different angles. There’s another book, another article, another person who explains it in a way that makes sense to you.
• It’s ok to be visual. We think of math as rigid and analytic — but visual interpretations are ok! Do what develops your understanding. Imaginary numbers were puzzling until their geometric interpretation came to light, decades after their initial discovery. Looking at equations all day didn’t help mathematicians “get” what they were about.

Math becomes difficult when we emphasize definitions over understanding. Remember that the modern definition is the most advanced step of thought, not necessarily the starting point. Don’t be afraid to approach a concept from a funny angle — figure out the plain-English sentence behind the equation. Happy math.

 

 

 

《数学:更好的解释》之培养数学直觉

对概念的第一印象塑造了我们对概念的直觉。 而且，直觉会影响我们对一个学科的喜爱程度。什么意思呢？比如，我们想给”猫”下个定义：

• 山顶洞人版 一个毛茸茸的动物，有爪子、牙齿、一条尾巴和四条腿。高兴的时候发出咕噜咕噜的声音，生气的时候嘶嘶的叫…
  
• 进化论版 某种哺乳类动物的后代，有着某些特征…
  
• 现代版 那些可以称之为定义？猫是一种动物，它们的DNA有着如下特征: ACATACATACATACAT…

毫无疑问，现代版本的定义是最准确的。但是它是最好的吗？你是这么给小孩子教授”猫”这个单词的？这个定义真的能更好揭示动物身上猫的特性吗？不见得。现代的定义是有用的，但是是在我们理解了猫是什么之后。我们不应该从现代的定义入手。

不幸的是，理解数学就像理解DNA一样。我们被教授了现代的，严谨的定义，但是却没有告诉我们这些概念什么怎么来的。留给我们的是一堆神秘的方程式，但是背后的原理是什么，我们却知之甚少。

让我们从不同的角度来探索一个概念。假想有一个圆：圆心是你正在学习的概念，圆的四周是对它的描述。我们从一个角落开始学习，仅仅依靠一个定理或者观点，然后努力思索不断加强我们的理解。我们从猫有着共同的身体特征推导出猫有共同的祖先，继而推导出一个物种可以通过特定的DNA进行区分。啊哈！我们现在可以知道猫的定义是如何从山顶洞人的定义演化到现在的定义了。

但是并不是所有的起点都是一样的。正确的视角使得我们学起来事半功倍 ——数学中发现定理的先驱们通常都具有启发式的观点。下面让我一起学习如何构建我们的直觉吧。

* 圆是什么 *
让我们来看一个数学示例：如何给圆下个定义？

看上去似乎有无数多个定义。下面举几个例子：

• 最对称的二维图形
  
• 用最少的周长围出最大面积的图形
  
• 平面中到定点距离相等点的集合
  
• 满足方程x^2 +y^2 = r^2点的集合
  
• 对所有的t，满足参数方程r*Sin(t),r*Cos(t)的点集合
  
• 切线始终与位置向量垂直的图形

这个清单还可以继续补充下去，但是有一个关键点：他们描述都描述了同一个概念。就像是说1（阿拉伯数字1），one（英文1）,uno（西班牙语1），eins（德语1），方程2x + 3 = 5的解，或者鼻子的个数。这些都表示数字1，只是同一个概念的不同的名字罢了。

但是这些初始的描述很重要——他们数造了我们的直觉。因为先在现实世界中见到了圆而后我们才在课堂中学习它，我们明白他们是“圆”的。无论我们觉得方程式（x^2 +y^2 = r^2 ）多么的令人惊艳，我们根深蒂固的知道圆圈是圆的。如果我们根据方程式进行作图，得到的图形是方的，或者不对称，那肯定是出错了。

做为小孩子，我们学习山顶洞人版的圆的定义（就是很圆的东西），给了我们很直观的直觉。我们发现在圆的东西上，所有点到中心的距离都是相等的。x^2 + y^2 = r^2是用解析的方法描述了同样的事实，使用了毕达哥拉斯的距离表示方法。我们从一个点出发根据我们的直觉，不断的学习然后推导出正式的定义。

其它的概念就未必如此幸运了。我们能够凭直觉了解到e表示增长率吗，或者它只是一个抽象的定义？我们能了解i（虚数概念）表示旋转吗，还是它只是一个人造的，没用的概念？

培养直觉的策略
时至今日我仍然需要时不时的提醒自己e与i的深层含义——这就像需要提醒自己就圈圈是圆的或者猫是什么样子一样荒唐！我们应该从最自然的想法开始学习他们。

忽略了重点使我抓狂：数学是关于概念的——方程式只是一种解释概念的方式而已。一定清楚了概念的要点，方程式很快就是建立起来。下面是一些对我有用的方法：

步骤1: 找出数学概念的主题。这个可能会很难，但是可以试着从它的历史着手。这个概念第一次出现在哪里？发现者做了哪些工作呢？概念之前的用途可能会和如今的解释和用途有所不同。

步骤2：通过一个主题来解释一个性质或定理。用一个主题来类比正式的定义。如果幸运的话，你可以把数学方程式（x^2 + y^2 = r^2）翻译成通俗易懂的语言。（“距离中心距离相等的点的集合”）

步骤3：使用相同的主题来挖掘相关连的性质。一定你发现了一个行之有效的类比或者解释，试试看是否它可以应用到其它的性质中。有时可以，有时不可以。这时候你需要重新审视了，但是你的发现会让你大吃一惊。

小试牛刀
一个实例：理解e
理解数字e是一项艰巨的任务。e出现在各种科学中，而且拥有多种定义，但是没有一个以一种自然的方式来定义。让我们围绕着这个概念做一些深入的探究。下面的几个小节会出现一些简单描述这个概念的方程式。纵然方程式看起来有些莫名其妙，但是其背后有隐藏着简单朴实的描述。
下面是一些e的定义：

第一步就是要寻找一个主题。查看一下e的历史，它好像和增长率或者利率相关。e是在做商业计算时发现的（而不是抽象的数学猜想），所以“利息”（增长率）就是个合适的主题。

我们来看一下第一个定义，图中左上角的那个。对我而言，最关键的跳跃是，认识到这个定义和复利计算公式有多像。事实上，这就你按照尽可能快的方式，在单位时间内以100%复利增长的条件下利率计算公式。

定义1：e定义为以最小的增量之下，以100%的复利增长所能达到的极限值。

这篇讲述e的文章(https://betterexplained.com/articles/an-intuitive-guide-to-exponential-functions-e/) 对上述定义做了详细的解释。让我们看一下第二个定义：一个无穷序列，后面每一项越来越小，这会是什么呢？

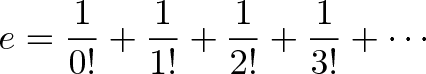
使用“利率”主题来深刻的探讨了这个定义。我们发现e的第二个定义是复利的组成部分。现在看起来还不是那么直观 – 我们思考一下在讨论增长率时，“1+1+1/2+1/6 …”代表了什么之后就可以柳暗花明了。

第一项（1=1/0!,记住0的阶乘等于1）是你的本金，初始资本。第二项（1=1/1!）是你直接赚的的利息 – 本金1的100%。第三项(0.5 = 1/2!) 是你利息赚得的利息（“第二级利息”）。接下来的一项(.1666 = 1/3!)是你的第三级利息–也就是你利息的利息所赚得的利息。

钱可生钱，生出来的钱还可以继续生钱，无穷无尽连绵不绝（子可生孙，孙又生子；子子孙孙，无穷匮也）– 这些无穷无尽的序列独立作出了贡献。还有很多东西可以说，但是还是让我们围绕增长率来理解这个概念吧。

定义2：e就是各项利息之和。

接下来我们来看e的第三个定义也是最短的一个。它是什么意思呢？不要去想着导数（这会把你的大脑切换到方程式模式）而是去想想它是什么。找找对方程式的感觉。让它成为你的朋友。

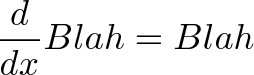
这是用微积分的方式表示“增长率等于现在的数量”。嗯，增长率等于现在的数值意味着100%的增长率，没错吧。而它是一直增长就意味着需要一直计算利率 – 这是用另一种方式来描述连续复合增长率。

定义3：e就是一个按照100%增长率在增长的函数。

很好——e就是一直完全按照自身的大小（100%）在增长的数，而不是1%或200%。

我们来看最后一个定义 – 最棘手的一个。我的解释是，相反我们不谈论增长了多少量，现在来谈一谈增长到一定量需要花费多少时间。

若果数值1按照100%的增长率，从1增长到2将花费1个单位的时间。但是如果从2开始并且以100%增长率增长，这意味着每个单位时间可以增长两倍。所以只要1/2单位时间就可以从2增长到3.从3增长到4值需要1/3单位时间就这样增长下去。从1增长到A的总时间是从1增到2，2到3，3到4 …… 直到增长到A为止花费的时间。利用第一个定义很自然就可以从“增长所耗的时间”的计算中定义“自然对数（ln）”。

ln(a)就是从1增长到a所需要花费的时间。我们可以将e称之为花费一单位时长可以增加多少。换言之，e就是一单位时长后所增长的部分！

定义4： 将从1连续增长到a所花费的时间为ln(a)。e就是经过1单位时间后所增加的量。

这就是描述神秘的e的四种方式。一定掌握了核心概念（e就是关于100%连续增长的）再复杂的方程式也可以搞得一清二楚 – 可以将微积分翻译成朴实的语言。数学就是关于概念的。

其中的寓意
在数学课上，我们通常从最新的复杂的概念开始学起。我们感到困惑并不意外：老师们给学生展示DNA结构而期望学生能够看到一只猫。

我从这个方法学到了不少经验教训，这直接造就了我如何理解以及解释数学：

• 探索其中的要义并应用它们。最初的直觉可以帮我们洞察很多事情做到一步到位。从一个有意义的定义开始，然后围绕着它不断的发现别的定义。
  
• 皮实一点。死记硬背概念并没什么卵用。如果不能茅塞顿开，试着换个角度。总有别的书籍，别的文章或者另外一些人可以帮助你理解。
  
• 可视化也很好。数学给人的感觉是严格的、解析的 – 但是可视化的解释也很好啊。虚数一直让人觉得很费解，直到他们的几何解释曝于人前，距发现虚数都好几十年了。整天盯着方程式看，数学家们也看不出个所以然来。

当我们过分强调定义本身而忽视对它的理解时，数学会变得很难学。记住，现在的定义是最先进的想法，并不是思想的源头。不要害怕从一个可笑的角度去接触概念 ，找出方程式背后最通俗易懂的语言。快乐的享受数学吧。