《算法导论》读书笔记(七)

《算法导论》读书笔记之第16章 贪心算法—活动选择问题

　　前言：贪心算法也是用来解决最优化问题，将一个问题分成子问题，在现在子问题最优解的时，选择当前看起来是最优的解，期望通过所做的局部最优选择来产生一个全局最优解。书中先从活动选择问题来引入贪心算法，分别采用动态规划方法和贪心算法进行分析。本篇笔记给出活动选择问题的详细分析过程，并给出详细的实现代码进行测试验证。关于贪心算法的详细分析过程，下次在讨论。

1、活动选择问题描述

　　  有一个需要使用每个资源的n个活动组成的集合S= {a₁，a₂，···，a_n }，资源每次只能由一个活动使用。每个活动a_i都有一个开始时间s_i和结束时间f_i，且 0≤s_i<f_i<∞ 。一旦被选择后，活动a_i就占据半开时间区间[s_i,f_i)。如果[s_i,f_i]和[s_j,f_j]互不重叠，则称a_i和a_j两个活动是兼容的。该问题就是要找出一个由互相兼容的活动组成的最大子集。例如下图所示的活动集合S，其中各项活动按照结束时间单调递增排序。

从图中可以看出S中共有11个活动，最大的相互兼容的活动子集为:{a₁，a₄，a₈，a11，}和{a₂，a₄，a₉，a₁₁}。

2、动态规划解决过程

（1）活动选择问题的最优子结构

定义子问题解空间S_ij是S的子集，其中的每个获得都是互相兼容的。即每个活动都是在a_i结束之后开始，且在a_j开始之前结束。

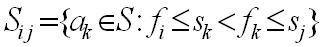
为了方便讨论和后面的计算，添加两个虚构活动a₀和a_n+1，其中f₀=0，s_n+1=∞。

结论：当i≥j时，S_ij为空集。

如果活动按照结束时间单调递增排序，子问题空间被用来从S_ij中选择最大兼容活动子集，其中0≤i＜j≤n+1，所以其他的S_ij都是空集。

最优子结构为：假设S_ij的最优解A_ij包含活动a_k，则对S_ik的解A_ik和S_kj的解A_kj必定是最优的。

通过一个活动a_k将问题分成两个子问题，下面的公式可以计算出S_ij的解A_ij。

（2）一个递归解

　　设c[i][j]为S_ij中最大兼容子集中的活动数目，当S_ij为空集时，c[i][j]=0；当S_ij非空时，若a_k在S_ij的最大兼容子集中被使用，则则问题S_ik和S_kj的最大兼容子集也被使用，故可得到c[i][j] = c[i][k]+c[k][j]+1。

当i≥j时，S_ij必定为空集，否则S_ij则需要根据上面提供的公式进行计算，如果找到一个a_k，则S_ij非空（此时满足f_i≤s_k且f_k≤s_j），找不到这样的a_k，则S_ij为空集。

c[i][j]的完整计算公式如下所示：

 

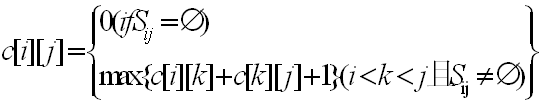
（3）最优解计算过程

　　根据递归公式，采用自底向下的策略进行计算c[i][j]，引入复杂数组ret[n][n]保存中间划分的k值。程序实现如下所示：

 1 void dynamic_activity_selector(int *s,int *f,int c[N+1][N+1],int ret[N+1][N+1])
 2 {
 3     int i,j,k;
 4     int temp;
 5     //当i>=j时候，子问题的解为空，即c[i][j]=0
 6     for(j=1;j<=N;j++)
 7       for(i=j;i<=N;i++)
 8          c[i][j] = 0;
 9     //当i<j时，需要寻找子问题的最优解，找到一个k使得将问题分成两部分
10     for(j=2;j<=N;j++)
11      for(i=1;i<j;i++)
12       {
13          //寻找k，将问题分成两个子问题c[i][k]、c[k][j] 
14          for(k=i+1;k<j;k++)
15             if(s[k] >= f[i] && f[k] <= s[j])   //判断k活动是否满足兼容性 
16              {
17                temp = c[i][k]+c[k][j]+1;
18                if(c[i][j] < temp)
19                 {
20                   c[i][j] =temp;
21                   ret[i][j] = k;
22                 }
23             }
24       }
25 }

 （4）构造一个最优解集合

　　根据第三保存的ret中的k值，递归调用输出获得集合。采用动态规划方法解决上面的例子，完整程序如下所示：

 

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 #define N 11
 5 
 6 void dynamic_activity_selector(int *s,int *f,int c[N+1][N+1],int ret[N+1][N+1]);
 7 void trace_route(int ret[N+1][N+1],int i,int j);
 8 
 9 int main()
10 {
11     int s[N+1] = {-1,1,3,0,5,3,5,6,8,8,2,12};
12     int f[N+1] = {-1,4,5,6,7,8,9,10,11,12,13,14};
13     int c[N+1][N+1]={0};
14     int ret[N+1][N+1]={0};
15     int i,j;
16     dynamic_activity_selector(s,f,c,ret);
17     printf("c[i][j]的值如下所示：\n");
18     for(i=1;i<=N;i++)
19     {
20         for(j=1;j<=N;j++)
21             printf("%d ",c[i][j]);
22         printf("\n");
23     }
24     //包括第一个和最后一个元素 
25     printf("最大子集的个数为: %d\n",c[1][N]+2); 
26     printf("ret[i][j]的值如下所示：\n");
27     for(i=1;i<=N;i++)
28     {
29         for(j=1;j<=N;j++)
30             printf("%d ",ret[i][j]);
31         printf("\n");
32     }
33     printf("最大子集为:{ a1 ");
34     trace_route(ret,1,N);
35     printf("a%d}\n",N);
36     system("pause");
37     return 0;
38 }
39 
40 void dynamic_activity_selector(int *s,int *f,int c[N+1][N+1],int ret[N+1][N+1])
41 {
42     int i,j,k;
43     int temp;
44     //当i>=j时候，子问题的解为空，即c[i][j]=0
45     for(j=1;j<=N;j++)
46       for(i=j;i<=N;i++)
47          c[i][j] = 0;
48     //当i>j时，需要寻找子问题的最优解，找到一个k使得将问题分成两部分
49     for(j=2;j<=N;j++)
50      for(i=1;i<j;i++)
51      {
52          //寻找k，将问题分成两个子问题c[i][k]、c[k][j] 
53          for(k=i+1;k<j;k++)
54             if(s[k] >= f[i] && f[k] <= s[j])   //判断k活动是否满足兼容性 
55             {
56                temp = c[i][k]+c[k][j]+1;
57                if(c[i][j] < temp)
58                {
59                   c[i][j] =temp;
60                   ret[i][j] = k;
61                }
62             }
63      }
64 }
65 
66 void trace_route(int ret[N+1][N+1],int i,int j)
67 {
68      if(i<j)
69      {
70          trace_route(ret,i,ret[i][j]);
71          if(ret[i][j] != 0 )  
72             printf("a%d ", ret[i][j]);
73      }
74 } 

 

程序测试结果如下所示：

3、贪心算法解决过程

针对活动选择问题，认真分析可以得出以下定理：对于任意非空子问题S_ij，设a_m是S_ij中具有最早结束时间的活动，那么：

（1）活动a_m在S_ij中的某最大兼容活动子集中被使用。

（2）子问题S_im为空，所以选择am将使子问题S_mj为唯一可能非空的子问题。

有这个定理，就简化了问题，使得最优解中只使用一个子问题，在解决子问题S_ij时，在S_ij中选择最早结束时间的那个活动。

贪心算法自顶向下地解决每个问题，解决子问题S_ij，先找到S_ij中最早结束的活动a_m，然后将a_m添加到最优解活动集合中，再来解决子问题S_mj。

基于这种思想可以采用递归和迭代进行实现。递归实现过程如下所示：

 1 void recursive_activity_selector(int *s,int* f,int i,int n,int *ret)
 2 {
 3      int *ptmp = ret;
 4      int m = i+1;
 5      //在Sin中寻找第一个结束的活动 
 6      while(m<=n && s[m] < f[i])
 7         m = m+1;
 8      if(m<=n)
 9      {
10         *ptmp++ = m;  //添加到结果中 
11         recursive_activity_selector(s,f,m,n,ptmp);
12      }
13 }

迭代实现过程如下：

 1 void greedy_activity_selector(int *s,int *f,int *ret)
 2 {
 3   int i,m;
 4   *ret++ = 1;
 5   i =1;
 6   for(m=2;m<=N;m++)
 7     if(s[m] >= f[i])
 8     {
 9        *ret++ = m;
10        i=m;
11     }
12 }

采用贪心算法实现上面的例子，完整代码如下所示：

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 #define N 11
 5 
 6 void recursive_activity_selector(int *s,int* f,int i,int n,int *ret);
 7 
 8 void greedy_activity_selector(int *s,int *f,int *ret); 
 9 
10 int main()
11 {
12     int s[N+1] = {-1,1,3,0,5,3,5,6,8,8,2,12};
13     int f[N+1] = {-1,4,5,6,7,8,9,10,11,12,13,14};
14     int c[N+1][N+1]={0};
15     int ret[N]={0};
16     int i,j;
17     //recursive_activity_selector(s,f,0,N,ret);
18     greedy_activity_selector(s,f,ret);
19     printf("最大子集为:{ ");
20     for(i=0;i<N;i++)
21     {
22        if(ret[i] != 0)
23          printf("a%d ",ret[i]);
24     }
25     printf(" }\n");
26     system("pause");
27     return 0;
28 }
29 
30 void recursive_activity_selector(int *s,int* f,int i,int n,int *ret)
31 {
32      int *ptmp = ret;
33      int m = i+1;
34      //在i和n中寻找第一个结束的活动 
35      while(m<=n && s[m] < f[i])
36         m = m+1;
37      if(m<=n)
38      {
39         *ptmp++ = m;  //添加到结果中 
40         recursive_activity_selector(s,f,m,n,ptmp);
41      }
42 }
43 
44 void greedy_activity_selector(int *s,int *f,int *ret)
45 {
46   int i,m;
47   *ret++ = 1;
48   i =1;
49   for(m=2;m<=N;m++)
50     if(s[m] >= f[i])
51     {
52        *ret++ = m;
53        i=m;
54     }
55 }

程序测试结果如下所示：

 4、总结

　　活动选择问题分别采用动态规划和贪心算法进行分析并实现。动态规划的运行时间为O(n^3)，贪心算法的运行时间为O(n)。动态规划解决问题时全局最优解中一定包含某个局部最优解，但不一定包含前一个局部最优解，因此需要记录之前的所有最优解。贪心算法的主要思想就是对问题求解时，总是做出在当前看来是最好的选择，产生一个局部最优解。

 

 

 

《算法导论》读书笔记之第16章 0-1背包问题—动态规划求解

1、前言

　　前段时间忙着搞毕业论文，看书效率不高，导致博客一个多月没有更新了。前段时间真是有些堕落啊，混日子的感觉，很少不爽。今天开始继续看算法导论。今天继续学习动态规划和贪心算法。首先简单的介绍一下动态规划与贪心算法的各自特点及其区别。然后针对0-1背包问题进行讨论。最后给出一个简单的测试例子，联系动态规划实现0-1背包问题。

2、动态规划与贪心算法

　　关于动态规划的总结请参考http://www.cnblogs.com/Anker/archive/2013/03/15/2961725.html。这里重点介绍一下贪心算法的过程。贪心算法是通过一系列的选择来给出某一个问题的最优解，每次选择一个当前（看起来是）最佳的选择。贪心算法解决问题的步骤为：

（1）决定问题的最优子结构

（2）设计出一个递归解

（3）证明在递归的任一阶段，最优选择之一总是贪心选择。保证贪心选择总是安全的。

（4）证明通过贪心选择，所有子问题（除一个意外）都为空。

（5）设计出一个实现贪心策略的递归算法。

（6）将递归算法转换成迭代算法。

　　什么时候才能使用贪心算法的呢？书中给出了贪心算法的两个性质，只有最优化问题满足这些性质，就可采用贪心算法解决问题。

（1）贪心选择性质：一个全局最优解可以通过举办最优解（贪心）选择来达到。即：当考虑做选择时，只考虑对当前问题最佳的选择而不考虑子问题的结果。而在动态规划中，每一步都要做出选择，这些选择依赖于子问题的解。动态规划一般是自底向上，从小问题到大问题。贪心算法通常是自上而下，一个一个地做贪心选择，不断地将给定的问题实例规约为更小的子问题。

（2）最优子结构：问题的一个最优解包含了其子问题的最优解。

动态规划与贪心的区别：

贪心算法： 
（1）贪心算法中，作出的每步贪心决策都无法改变，因为贪心策略是由上一步的最优解推导下一步的最优解，而上一部之前的最优解则不作保留； 
（2）由（1）中的介绍，可以知道贪心法正确的条件是：每一步的最优解一定包含上一步的最优解。 

动态规划算法： 
（1）全局最优解中一定包含某个局部最优解，但不一定包含前一个局部最优解，因此需要记录之前的所有最优解 ；
（2）动态规划的关键是状态转移方程，即如何由以求出的局部最优解来推导全局最优解 ；
（3）边界条件：即最简单的，可以直接得出的局部最优解。

3、0-1背包问题描述

　　有一个窃贼在偷窃一家商店时发现有n件物品，第i件物品价值为v_i元，重量为w_i，假设v_i和w_i都为整数。他希望带走的东西越值钱越好，但他的背包中之多只能装下W磅的东西，W为一整数。他应该带走哪几样东西？

0-1背包问题中：每件物品或被带走，或被留下，（需要做出0-1选择）。小偷不能只带走某个物品的一部分或带走两次以上同一个物品。

部分背包问题：小偷可以只带走某个物品的一部分，不必做出0-1选择。

4、0-1背包问题解决方法

　　0-1背包问题是个典型举办子结构的问题，但是只能采用动态规划来解决，而不能采用贪心算法。因为在0-1背包问题中，在选择是否要把一个物品加到背包中，必须把该物品加进去的子问题的解与不取该物品的子问题的解进行比较。这种方式形成的问题导致了许多重叠子问题，满足动态规划的特征。动态规划解决0-1背包问题步骤如下：

0-1背包问题子结构：选择一个给定物品i，则需要比较选择i的形成的子问题的最优解与不选择i的子问题的最优解。分成两个子问题，进行选择比较，选择最优的。

0-1背包问题递归过程：设有n个物品，背包的重量为w，C[i][w]为最优解。即：

课后习题给出了伪代码：

5、编程实现

　　现在给定3个物品，背包的容量为50磅。物品1重10磅，价值为60，物品2重20磅，价值为100，物品3重30磅，价值为120。采用动态规划可以知道最优解为220，选择物品2和3。采用C++语言实现如下：

 1 #include <iostream>
 2 using namespace std;
 3 
 4 //物品数据结构
 5 typedef struct commodity
 6 {
 7     int value;  //价值
 8     int weight; //重量
 9 }commodity;
10 
11 const int N = 3;  //物品个数
12 const int W = 50; //背包的容量
13 
14 //初始物品信息
15 commodity goods[N+1]={{0,0},{60,10},{100,20},{120,30}};
16 int select[N+1][W+1];
17 
18 int max_value();
19 
20 int main()
21 {
22     int maxvalue = max_value();
23     cout<<"The max value is: ";
24     cout<<maxvalue<<endl;
25     int remainspace = W;
26     //输出所选择的物品列表：
27     for(int i=N; i>=1; i--)
28     {
29         if (remainspace >= goods[i].weight)
30         {
31              if ((select[i][remainspace]-select[i-1][remainspace-goods[i].weight]==goods[i].value))
32              {
33                  cout << "item " << i << " is selected!" << endl;
34                  remainspace = remainspace - goods[i].weight;//如果第i个物品被选择，那么背包剩余容量将减去第i个物品的重量 ;
35              }
36         }
37     }
38     return 0;
39 }
40 int max_value()
41 {
42     //初始没有物品时候，背包的价值为0
43     for(int w=1;w<=W;++w)
44         select[0][w] = 0;
45     for(int i=1;i<=N;++i)
46     {
47         select[i][0] = 0;  //背包容量为0时，最大价值为0
48            for(int w=1;w<=W;++w)
49            {
50                if(goods[i].weight <= w)  //当前物品i的重量小于等于w，进行选择
51                {
52                    if( (goods[i].value + select[i-1][w-goods[i].weight]) > select[i-1][w])
53                     select[i][w] = goods[i].value + select[i-1][w-goods[i].weight];
54                    else
55                     select[i][w] = select[i-1][w];
56                }
57                else //当前物品i的重量大于w，不选择
58                  select[i][w] = select[i-1][w];
59            }
60     }
61     return select[N][W];  //最终求得最大值
62 }

程序测试结果如下：