图的基本概念
图的基本概念
1. 图的定义
定义:图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的;其中,点通常被成为"顶点(vertex)",而点与点之间的连线则被成为"边或弧"(edege)。通常记为,G=(V,E)。
2. 图的种类
根据边是否有方向,将图可以划分为:无向图和有向图。
2.1 无向图
上面的图G0是无向图,无向图的所有的边都是不区分方向的。G0=(V1,{E1})。其中,
(01) V1={A,B,C,D,E,F}。 V1表示由"A,B,C,D,E,F"几个顶点组成的集合。
(02) E1={(A,B),(A,C),(B,C),(B,E),(B,F),(C,F), (C,D),(E,F),(C,E)}。 E1是由边(A,B),边(A,C)...等等组成的集合。其中,(A,C)表示由顶点A和顶点C连接成的边。
2.2 有向图
上面的图G2是有向图。和无向图不同,有向图的所有的边都是有方向的! G2=(V2,{A2})。其中,
(01) V2={A,C,B,F,D,E,G}。 V2表示由"A,B,C,D,E,F,G"几个顶点组成的集合。
(02) A2={<A,B>,<B,C>,<B,F>,<B,E>,<C,E>,<E,D>,<D,C>,<E,B>,<F,G>}。
E1是由矢量<A,B>,矢量<B,C>...等等组成的集合。其中,矢量<A,B)表示由"顶点A"指向"顶点C"的有向边。
3. 邻接点和度
3.1 邻接点
一条边上的两个顶点叫做邻接点。
例如,上面无向图G0中的顶点A和顶点C就是邻接点。
在有向图中,除了邻接点之外;还有"入边"和"出边"的概念。
顶点的入边,是指以该顶点为终点的边。而顶点的出边,则是指以该顶点为起点的边。
例如,上面有向图G2中的B和E是邻接点;<B,E>是B的出边,还是E的入边。
3.2 度
在无向图中,某个顶点的度是邻接到该顶点的边(或弧)的数目。
例如,上面无向图G0中顶点A的度是2。
在有向图中,度还有"入度"和"出度"之分。
某个顶点的入度,是指以该顶点为终点的边的数目。而顶点的出度,则是指以该顶点为起点的边的数目。
顶点的度=入度+出度。
例如,上面有向图G2中,顶点B的入度是2,出度是3;顶点B的度=2+3=5。
4. 路径和回路
路径:如果顶点(Vm)到顶点(Vn)之间存在一个顶点序列。则表示Vm到Vn是一条路径。
路径长度:路径中"边的数量"。
简单路径:若一条路径上顶点不重复出现,则是简单路径。
回路:若路径的第一个顶点和最后一个顶点相同,则是回路。
简单回路:第一个顶点和最后一个顶点相同,其它各顶点都不重复的回路则是简单回路。
5. 连通图和连通分量
连通图:对无向图而言,任意两个顶点之间都存在一条无向路径,则称该无向图为连通图。 对有向图而言,若图中任意两个顶点之间都存在一条有向路径,则称该有向图为强连通图。
连通分量:非连通图中的各个连通子图称为该图的连通分量。
6. 权
在学习"哈夫曼树"的时候,了解过"权"的概念。图中权的概念与此类似。
上面就是一个带权的图。
图的存储结构
上面了解了"图的基本概念",下面开始介绍图的存储结构。图的存储结构,常用的是"邻接矩阵"和"邻接表"。
1. 邻接矩阵
邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。
假设图中顶点数为n,则邻接矩阵定义为:
下面通过示意图来进行解释。
图中的G1是无向图和它对应的邻接矩阵。
图中的G2是无向图和它对应的邻接矩阵。
通常采用两个数组来实现邻接矩阵:一个一维数组用来保存顶点信息,一个二维数组来用保存边的信息。
邻接矩阵的缺点就是比较耗费空间。
2. 邻接表
邻接表是图的一种链式存储表示方法。它是改进后的"邻接矩阵",它的缺点是不方便判断两个顶点之间是否有边,但是相对邻接矩阵来说更省空间。
图中的G1是无向图和它对应的邻接矩阵。
图中的G2是无向图和它对应的邻接矩阵。
邻接表无向图的介绍
邻接表无向图是指通过邻接表表示的无向图。
上面的图G1包含了"A,B,C,D,E,F,G"共7个顶点,而且包含了"(A,C),(A,D),(A,F),(B,C),(C,D),(E,G),(F,G)"共7条边。
上图右边的矩阵是G1在内存中的邻接表示意图。每一个顶点都包含一条链表,该链表记录了"该顶点的邻接点的序号"。例如,第2个顶点(顶点C)包含的链表所包含的节点的数据分别是"0,1,3";而这"0,1,3"分别对应"A,B,D"的序号,"A,B,D"都是C的邻接点。就是通过这种方式记录图的信息的。
邻接表无向图的代码说明
1. 基本定义
// 邻接表中表对应的链表的顶点
typedef struct _ENode
{
int ivex; // 该边所指向的顶点的位置
struct _ENode *next_edge; // 指向下一条弧的指针
}ENode, *PENode;
// 邻接表中表的顶点
typedef struct _VNode
{
char data; // 顶点信息
ENode *first_edge; // 指向第一条依附该顶点的弧
}VNode;
// 邻接表
typedef struct _LGraph
{
int vexnum; // 图的顶点的数目
int edgnum; // 图的边的数目
VNode vexs[MAX];
}LGraph;
(01) LGraph是邻接表对应的结构体。
vexnum是顶点数,edgnum是边数;vexs则是保存顶点信息的一维数组。
(02) VNode是邻接表顶点对应的结构体。
data是顶点所包含的数据,而first_edge是该顶点所包含链表的表头指针。
(03) ENode是邻接表顶点所包含的链表的节点对应的结构体。
ivex是该节点所对应的顶点在vexs中的索引,而next_edge是指向下一个节点的。
2. 创建矩阵
2.1 创建图(用已提供的矩阵)
C语言实现代码:
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
typedef struct graph
{
char vexs[MAX];
int vexnum;
int edgnum;
int matrix[MAX][MAX];
}Graph,*PGraph;
static int get_position(Graph g,char ch)
{
int i;
for(i=0;i<g.vexnum;i++)
if(g.vexs[i]==ch)
return i;
return -1;
}
Graph* create_graph()
{
char vexs[]={'A','B','C','D','E','F','G'};
char edges[][2]={{'A','C'},{'A','D'},{'A','F'},{'B','C'},{'C','D'},{'E','G'},{'F','G'}};
int vlen=sizeof(vexs)/sizeof(vexs[0]);
int elen=sizeof(edges)/sizeof(edges[0]);
int i,p1,p2;
Graph *pG;
if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
return NULL;
memset(pG,0,sizeof(Graph));
pG->vexnum=vlen;
pG->edgnum=elen;
for(i=0;i<pG->vexnum;i++)
{
pG->vexs[i]=vexs[i];
}
for(i=0;i<pG->edgnum;i++)
{
p1=get_position(*pG,edges[i][0]);
p2=get_position(*pG,edges[i][1]);
pG->matrix[p1][p2]=1;
pG->matrix[p2][p1]=1;
}
return pG;
}
void print_graph(Graph G)
{
int i,j;
printf("matrix Graph:\n");
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.vexnum;j++)
printf("%d ",G.matrix[i][j]);
printf("\n");
}
}
int main()
{
Graph *pG;
pG=create_graph();
print_graph(*pG);
}
运行结果:
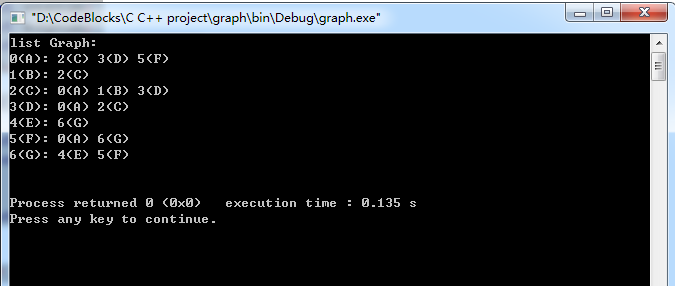
邻接表有向图的介绍
邻接表有向图是指通过邻接表表示的有向图。
上面的图G2包含了"A,B,C,D,E,F,G"共7个顶点,而且包含了"<A,B>,<B,C>,<B,E>,<B,F>,<C,E>,<D,C>,<E,B>,<E,D>,<F,G>"共9条边。
上图右边的矩阵是G2在内存中的邻接表示意图。每一个顶点都包含一条链表,该链表记录了"该顶点所对应的出边的另一个顶点的序号"。例如,第1个顶点(顶点B)包含的链表所包含的节点的数据分别是"2,4,5";而这"2,4,5"分别对应"C,E,F"的序号,"C,E,F"都属于B的出边的另一个顶点。
邻接表有向图的代码说明
1. 基本定义
// 邻接表中表对应的链表的顶点
typedef struct _ENode
{
int ivex; // 该边所指向的顶点的位置
struct _ENode *next_edge; // 指向下一条弧的指针
}ENode, *PENode;
// 邻接表中表的顶点
typedef struct _VNode
{
char data; // 顶点信息
ENode *first_edge; // 指向第一条依附该顶点的弧
}VNode;
// 邻接表
typedef struct _LGraph
{
int vexnum; // 图的顶点的数目
int edgnum; // 图的边的数目
VNode vexs[MAX];
}LGraph;
(01) LGraph是邻接表对应的结构体。 vexnum是顶点数,edgnum是边数;vexs则是保存顶点信息的一维数组。
(02) VNode是邻接表顶点对应的结构体。 data是顶点所包含的数据,而firstedge是该顶点所包含链表的表头指针。
(03) ENode是邻接表顶点所包含的链表的节点对应的结构体。 ivex是该节点所对应的顶点在vexs中的索引,而nextedge是指向下一个节点的。
2. 创建矩阵
邻接表C实现代码:
#include<stdlib.h>
#include<stdio.h>
#include<string.h>
#include<malloc.h>
#define MAX 100
typedef struct ENode
{
int ivex;
struct ENode *next_edge;
}ENode;
typedef struct VNode
{
char data;
struct ENode *first_edge;
}VNode;
typedef struct LGraph
{
int vexnum;
int edgnum;
VNode vexs[MAX];
}LGraph;
int get_position(LGraph g,char ch)
{
int i;
for(i=0;i<g.vexnum;i++)
if(ch==g.vexs[i].data)
return i;
return -1;
}
LGraph* create_graph()
{
char vexs[]= {'A','B','C','D','E','F','G'};
char edges[][2]= {{'A','C'},{'A','D'},{'A','F'},{'B','C'},{'C','D'},{'E','G'},{'F','G'}};
int vlen=sizeof(vexs)/sizeof(vexs[0]);
int elen=sizeof(edges)/sizeof(edges[0]);
int i,p1,p2;
ENode *node2;
LGraph *pG;
if((pG=(LGraph*)malloc(sizeof(LGraph)))==NULL)
return NULL;
memset(pG,0,sizeof(pG));
pG->edgnum=elen;
pG->vexnum=vlen;
for(i=0;i<pG->vexnum;i++)
{
pG->vexs[i].data=vexs[i];
pG->vexs[i].first_edge=NULL;
}
for(i=0;i<pG->edgnum;i++)
{
p1=get_position(*pG,edges[i][0]);
p2=get_position(*pG,edges[i][1]);
node2=(ENode*)malloc(sizeof(ENode));
node2->ivex=p2;
node2->next_edge=NULL;
if(pG->vexs[p1].first_edge==NULL)
pG->vexs[p1].first_edge=node2;
else
{
ENode *tmp=pG->vexs[p1].first_edge;
while(tmp->next_edge)
{
tmp=tmp->next_edge;
}
tmp->next_edge=node2;
}
}
return pG;
}
void print_graph(LGraph G)
{
int i;
printf("List Graph:\n");
ENode *node=NULL;
for(i=0;i<G.vexnum;i++)
{
printf("%d(%c): ", i, G.vexs[i].data);
node=G.vexs[i].first_edge;
while(node)
{
printf("%d(%c) ", node->ivex, G.vexs[node->ivex].data);
node=node->next_edge;
}
printf("\n");
}
}
int main()
{
LGraph *pG;
pG=create_graph();
print_graph(*pG);
}
运行结果:
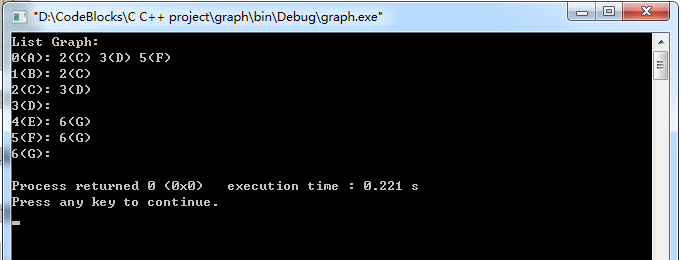
邻接矩阵无向图的介绍
邻接矩阵无向图是指通过邻接矩阵表示的无向图。
上面的图G1包含了"A,B,C,D,E,F,G"共7个顶点,而且包含了"(A,C),(A,D),(A,F),(B,C),(C,D),(E,G),(F,G)"共7条边。由于这是无向图,所以边(A,C)和边(C,A)是同一条边;这里列举边时,是按照字母先后顺序列举的。
上图右边的矩阵是G1在内存中的邻接矩阵示意图。A[i][j]=1表示第i个顶点与第j个顶点是邻接点,A[i][j]=0则表示它们不是邻接点;而A[i][j]表示的是第i行第j列的值;例如,A[1,2]=1,表示第1个顶点(即顶点B)和第2个顶点(C)是邻接点。
邻接矩阵无向图的代码说明
1. 基本定义
// 邻接矩阵
typedef struct _graph
{
char vexs[MAX]; // 顶点集合
int vexnum; // 顶点数
int edgnum; // 边数
int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;
Graph是邻接矩阵对应的结构体。
vexs用于保存顶点,vexnum是顶点数,edgnum是边数;matrix则是用于保存矩阵信息的二维数组。例如,matrix[i][j]=1,则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点;matrix[i][j]=0,则表示它们不是邻接点。
2. 创建矩阵
这里介绍提供了两个创建矩阵的方法。一个是用已知数据,另一个则需要用户手动输入数据。
2.1 创建图(用已提供的矩阵)
/*
* 创建图(用已提供的矩阵)
*/
Graph* create_example_graph()
{
char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
char edges[][2] = {
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'F', 'G'}};
int vlen = LENGTH(vexs);
int elen = LENGTH(edges);
int i, p1, p2;
Graph* pG;
// 输入"顶点数"和"边数"
if ((pG=(Graph*)malloc(sizeof(Graph))) == NULL )
return NULL;
memset(pG, 0, sizeof(Graph));
// 初始化"顶点数"和"边数"
pG->vexnum = vlen;
pG->edgnum = elen;
// 初始化"顶点"
for (i = 0; i < pG->vexnum; i++)
{
pG->vexs[i] = vexs[i];
}
// 初始化"边"
for (i = 0; i < pG->edgnum; i++)
{
// 读取边的起始顶点和结束顶点
p1 = get_position(*pG, edges[i][0]);
p2 = get_position(*pG, edges[i][1]);
pG->matrix[p1][p2] = 1;
pG->matrix[p2][p1] = 1;
}
return pG;
}
createexamplegraph是的作用是创建一个邻接矩阵无向图。
注意:该方法创建的无向图,就是上面图G1。
邻接矩阵无向图的完整源码
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
typedef struct graph
{
char vexs[MAX];
int vexnum;
int edgnum;
int matrix[MAX][MAX];
}Graph,*PGraph;
static int get_position(Graph g,char ch)
{
int i;
for(i=0;i<g.vexnum;i++)
if(g.vexs[i]==ch)
return i;
return -1;
}
Graph* create_graph()
{
char vexs[]={'A','B','C','D','E','F','G'};
char edges[][2]={{'A','C'},{'A','D'},{'A','F'},{'B','C'},{'C','D'},{'E','G'},{'F','G'}};
int vlen=sizeof(vexs)/sizeof(vexs[0]);
int elen=sizeof(edges)/sizeof(edges[0]);
int i,p1,p2;
Graph *pG;
if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
return NULL;
memset(pG,0,sizeof(Graph));
pG->vexnum=vlen;
pG->edgnum=elen;
for(i=0;i<pG->vexnum;i++)
{
pG->vexs[i]=vexs[i];
}
for(i=0;i<pG->edgnum;i++)
{
p1=get_position(*pG,edges[i][0]);
p2=get_position(*pG,edges[i][1]);
pG->matrix[p1][p2]=1;
pG->matrix[p2][p1]=1;
}
return pG;
}
void print_graph(Graph G)
{
int i,j;
printf("matrix Graph:\n");
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.vexnum;j++)
printf("%d ",G.matrix[i][j]);
printf("\n");
}
}
int main()
{
Graph *pG;
pG=create_graph();
print_graph(*pG);
}
运行结果:

邻接矩阵有向图的介绍
邻接矩阵有向图的介绍
邻接矩阵有向图是指通过邻接矩阵表示的有向图。
上面的图G2包含了"A,B,C,D,E,F,G"共7个顶点,而且包含了"<A,B>,<B,C>,<B,E>,<B,F>,<C,E>,<D,C>,<E,B>,<E,D>,<F,G>"共9条边。
上图右边的矩阵是G2在内存中的邻接矩阵示意图。A[i][j]=1表示第i个顶点到第j个顶点是一条边,A[i][j]=0则表示不是一条边;而A[i][j]表示的是第i行第j列的值;例如,A[1,2]=1,表示第1个顶点(即顶点B)到第2个顶点(C)是一条边。
邻接矩阵有向图的代码说明
1. 基本定义
// 邻接矩阵
typedef struct _graph
{
char vexs[MAX]; // 顶点集合
int vexnum; // 顶点数
int edgnum; // 边数
int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;
Graph是邻接矩阵对应的结构体。
vexs用于保存顶点,vexnum是顶点数,edgnum是边数;matrix则是用于保存矩阵信息的二维数组。例如,matrix[i][j]=1,则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点;matrix[i][j]=0,则表示它们不是邻接点。
2. 创建矩阵
C实现代码:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<malloc.h>
#define MAX 100
typedef struct graph
{
char vexs[MAX];
int vexnum;
int edgnum;
int matrix[MAX][MAX];
} Graph,*graph;
static int get_position(Graph g,char ch)
{
int i;
for(i=0;i<g.vexnum;i++)
if(g.vexs[i]==ch)
return i;
return -1;
}
graph create_graph()
{
char vexs[]= {'A','B','C','D','E','F','G'};
char edges[][2]= {{'A','C'},{'A','D'},{'A','F'},{'B','C'},{'C','D'},{'E','G'},{'F','G'}};
int vlen=sizeof(vexs)/sizeof(vexs[0]);
int elen=sizeof(edges)/sizeof(edges[0]);
int i,p1,p2;
Graph *pG;
if((pG=(graph)malloc(sizeof(Graph)))==NULL)
return NULL;
pG->edgnum=elen;
pG->vexnum=vlen;
for(i=0;i<pG->vexnum;i++)
pG->vexs[i]=vexs[i];
for(i=0;i<pG->edgnum;i++)
{
p1=get_position(*pG,edges[i][0]);
p2=get_position(*pG,edges[i][1]);
pG->matrix[p1][p2]=1;
}
return pG;
}
void print_graph(Graph G)
{
int i,j;
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.edgnum;j++)
{
printf("%d ",G.matrix[i][j]);
}
printf("\n");
}
printf("\n");
}
int main()
{
Graph *pG;
pG=create_graph();
print_graph(*pG);
}
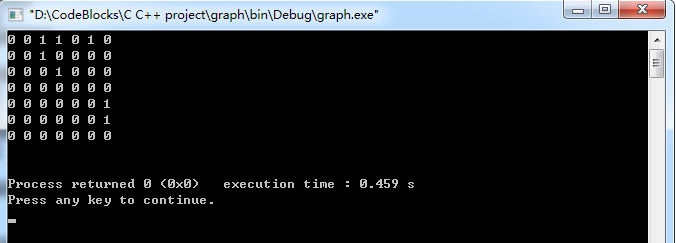
运行结果: