prim算法

一个连通图的生成树是一个极小的连通子图，它包含图中全部的顶点（n个顶点），但只有n-1条边。

最小生成树：构造连通网的最小代价（最小权值）生成树。

prim算法在严蔚敏树上有解释，但是都是数学语言，很深奥。

最小生成树MST性质：假设N=（V,{E}）是一个连通网，U是顶点集V的一个非空子集。若（u,v）是一条具有最小权值（代价）的边，

其中u∈U，v∈V-U，则必存在一颗包含边（u,v）的最小生成树。

prim算法过程为：

假设N=（V,{E}）是连通图，TE是N上最小生成树中边的集合。算法从U={u₀}（u₀∈V），TE={}开始，

重复执行下述操作：

在所有u∈U，v∈V-U的边（u，v）∈E中找一条代价最小的边（u₀，v₀）并入集合TE，同时v₀并入U，直至U=V为止。

此时TE中必有n-1条边，则T=（V，{TE}）为N的最小生成树。

我以图为例，看看算法过程。

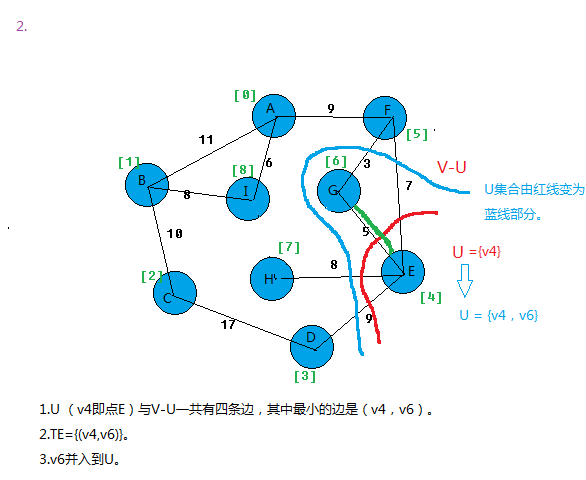
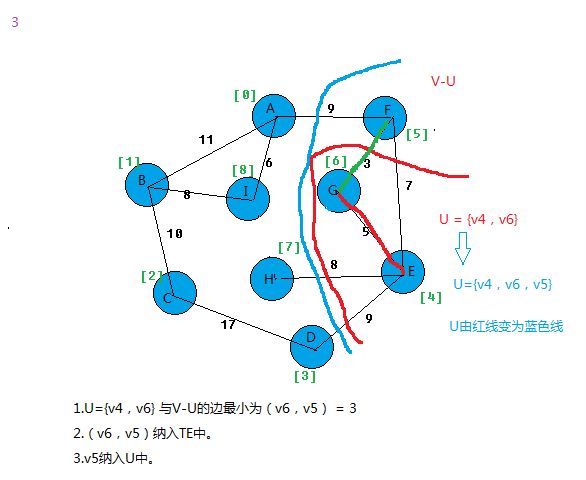
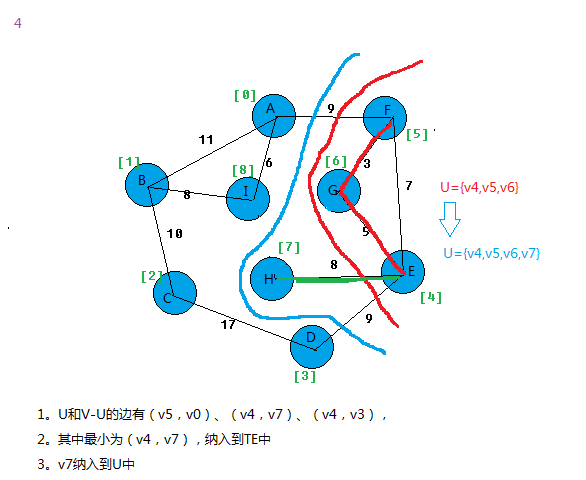
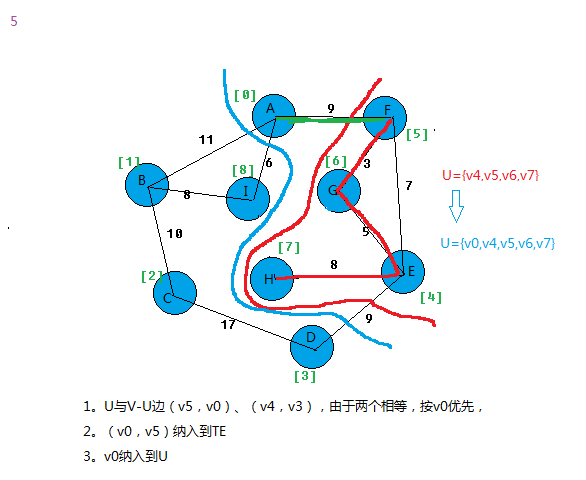
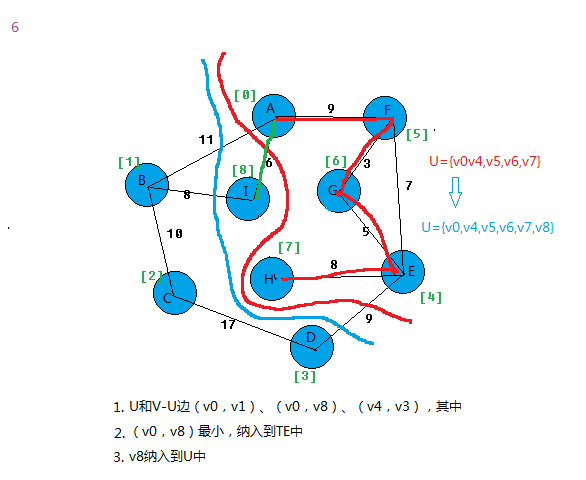
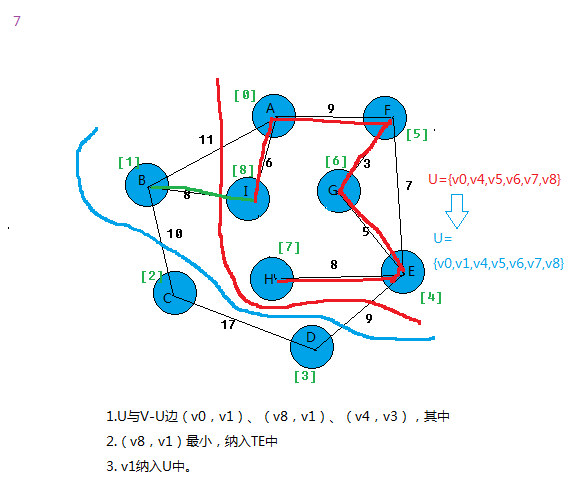
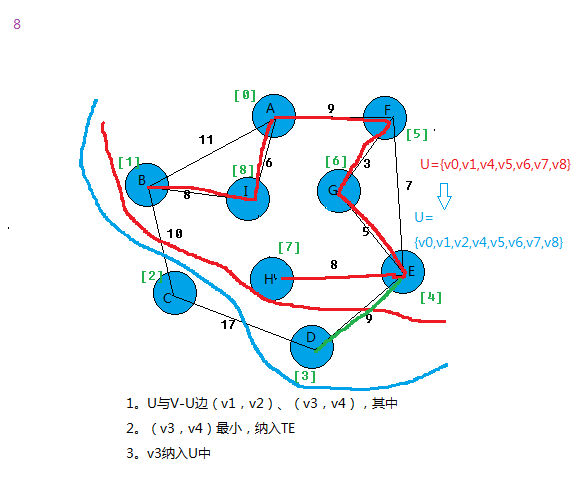
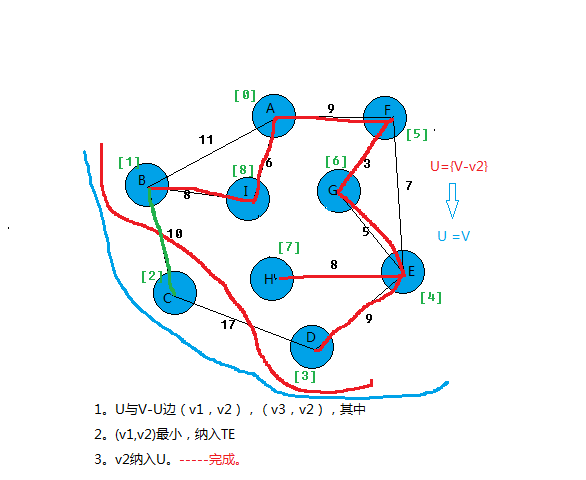
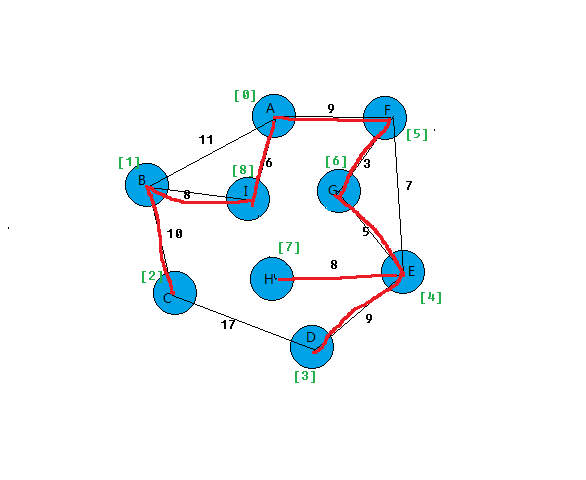
上面基本就把prim算法思想给表达出来。

代码部分：

这里我使用的是邻接矩阵来表示图，其中边的值就是权值。

#include<stdio.h>
#include<stdlib.h>
typedef int bool;
typedef char VertexType;
typedef int  EdgeType;
#define false 0
#define true 1
#define MAXVEX 100
#define IFY 65535

VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'};

EdgeType g_init_edges[MAXVEX][MAXVEX] = {
    {0,11,IFY,IFY,IFY,9,IFY,IFY,6},    //'A'
    {11,0,10,IFY,IFY,IFY,IFY,IFY,8},  //'B'
    {IFY,10,0,17,IFY,IFY,IFY,IFY,IFY},//'C'
    {IFY,IFY,17,0,9,IFY,IFY,IFY,IFY},//'D'
    {IFY,IFY,IFY,9,0,7,5,8,IFY},    //'E'
    {9,IFY,IFY,IFY,7,0,3,IFY,IFY},    //'F'
    {IFY,IFY,IFY,IFY,5,3,0,IFY,IFY},    //'G'
    {IFY,IFY,IFY,IFY,8,IFY,IFY,0,IFY},    //'H'
    {6,8,IFY,IFY,IFY,IFY,IFY,IFY,0},    //'I'
};

typedef struct {
    VertexType vexs[MAXVEX];
    EdgeType Mat[MAXVEX][MAXVEX];
    int numVexs,numEdges;
}MGraph;

//打印矩阵,使用二维指针
void prt_maxtix(EdgeType (*p)[MAXVEX],int vexs)
{
    int i,j;
    for(i=0;i<vexs;i++)
    {
        printf("\t");
        for(j=0;j<vexs;j++)
        {
             if( *(*p + j) == IFY)
            {
                printf("  $ ");
            }
            else
            {
                printf(" %2d ", *(*p + j));
            }
        }
         p++;
         printf("\n");
    }
}

//check the number of vextex
int getVexNum(VertexType *vexs)
{
    VertexType *pos = vexs;
    int cnt=0;
    while(*pos <= 'Z' && *pos >= 'A')
    {
        cnt++;
        pos++;
    }
    return cnt;
}
//检查矩阵是否对称
bool checkMat(EdgeType *p,VertexType numvex)
{
    int i,j;
    for (i=0;i<numvex;i++)
    {
        for(j=i+1;j<numvex;j++)
        {
            //printf("[%d][%d] = %d\t",i,j,*(p + MAXVEX*i + j));
            //printf("[%d][%d] = %d\n",j,i,*(p + MAXVEX*j + i));
            if (*(p + MAXVEX*i + j) != *(p + MAXVEX*j +i) )
            {
                printf("ERROR:Mat[%d][%d] or Mat[%d][%d] not equal!\n",i,j,j,i);
                return false;
            }
        }
    }
    return true;
}
//用已知的一维数组和二维数组分别初始化顶点和边
void init_Grp(MGraph *g,VertexType *v,EdgeType *p)
{
    int i,j;
    // init vex num
    (*g).numVexs = getVexNum(v);

    //init vexter
    for (i=0;i<(*g).numVexs;i++)
    {
        (*g).vexs[i]=*v;
        v++;
    }

    //init Mat
    for (i=0;i<(*g).numVexs;i++)
    {
        for (j=0;j<(*g).numVexs;j++)
        {
            (*g).Mat[i][j] = *(p + MAXVEX*i + j);
        }
    }
    if(checkMat(&((*g).Mat[0][0]),(*g).numVexs) == false)
    {
        printf("init error!\n");
        exit(0);
    }
}

/*void prim(MGraph G,int num)
{
    int sum=0;
    int min,i,j,k;
    int adjvex[MAXVEX];
    int lowcost[MAXVEX];

    lowcost[num] = 0;
    adjvex[num] = 0;

    for (i = 0; i < G.numVexs;i++ )
    {
        if (num == i)
        {
            continue;
        }
        lowcost[i]=G.Mat[num][i];    //存放起始顶点到各个顶点的权值。
        adjvex[i] = num;
    }

    for (i=0;i<G.numVexs;i++)
    {
        //1.找权最短路径
        //2.把权最短路径的顶点纳入已找到的顶点集合中，重新查看新集合中最短路径
        if(num == i)
        {
            continue;
        }
        min = IFY;
        j=0;k=0;
        while (j<G.numVexs)
        {
            if (lowcost[j] != 0 && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j;

            }
            j++;
        }
        printf(" (%d,%d) --> ",adjvex[k],k);
        sum += G.Mat[adjvex[k]][k];
        lowcost[k]=0;
        for (j=0;j<G.numVexs;j++)
        {

            if (lowcost[j] != 0 && G.Mat[k][j] < lowcost[j])
            {
                lowcost[j] = G.Mat[k][j];
                adjvex[j]=k;
            }
        }

    }
    printf("total:sum=%d\n",sum);
}*/

void Prim(MGraph G,int num)
{
    int sum,i,j,min,k;
    int adjvex[MAXVEX];
    int lowcost[MAXVEX];
    sum=0;
    adjvex[num]=0;
    lowcost[num]=0;
    for(i=0;i<G.numVexs;i++)
    {
        if(i==num)
            continue;
        adjvex[i]=num;
        lowcost[i]=G.Mat[num][i];
    }
    for(i=0;i<G.numVexs;i++)
    {
        if(i==num)
            continue;
        min=IFY;
        k=0;
        //求出代价最小的点
        for(j=0;j<G.numVexs;j++)
        {
            if(lowcost[j]!=0&&lowcost[j]<min)
            {
                min=lowcost[j];
                k=j;
            }
        }
        printf("(%d,%d)-->",adjvex[k],k);
        sum+=G.Mat[adjvex[k]][k];
        lowcost[k]=0;
        for(j=0;j<G.numVexs;j++)
        {
            if(lowcost[j]!=0&&G.Mat[k][j]<lowcost[j])
            {
                lowcost[j]=G.Mat[k][j];
                adjvex[j]=k;
            }
        }
    }
    printf("total:sum=%d\n",sum);
}

int main(int argc, char* argv[])
{
    MGraph grp;
    //init
    init_Grp(&grp,g_init_vexs,&g_init_edges[0][0]);
    //print Matix
    prt_maxtix(grp.Mat,grp.numVexs);

    //prim(grp,4);
    int i;
    for (i=0;i<grp.numVexs;i++)
    {
        Prim(grp,i);
    }
    //prim(grp,3);


    getchar();
    return 0;
}

运行结果如下：

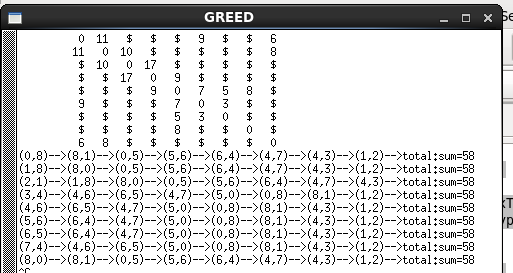
Jungle Roads

Problem Description

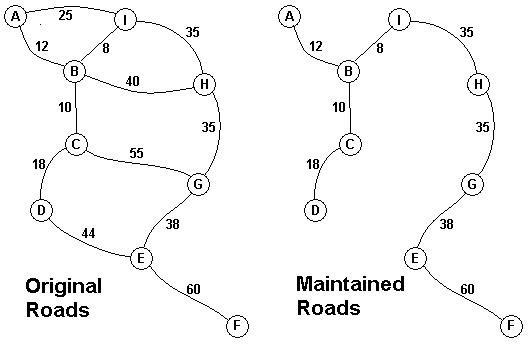
The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems.

The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above.

The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit.

Sample Input

9 A 2 B 12 I 25 B 3 C 10 H 40 I 8 C 2 D 18 G 55 D 1 E 44 E 2 F 60 G 38 F 0 G 1 H 35 H 1 I 35 3 A 2 B 10 C 40 B 1 C 20 0

Sample Output

216
30

//HDOJ1301
#include<iostream>
#include<cstring>
using namespace std;
#define MAX 99999
#define LEN 30
int dist[LEN];//某点的权值  起始点到目标点的权值
int map[LEN][LEN];//某点到某点两点之间的权值
bool isvisitd[LEN];//表示某点是否访问过

//初始化map数组  设置为无穷大
void  init(int n){
    for(int  i = 0;i<=n;i++) {
         for(int  j = 0;j<=n;j++)
            map[i][j] = MAX; 
     } 
} 

//prim最小生成树的算法
int prim(int n){
    int i,j,min,pos,sum; 
    sum = 0;   //最小生成树的权值

    //初始化，表示没有一点走过
    memset(isvisitd,false,sizeof(isvisitd));
    
    //初始化给dist数组赋值
    for(i = 1;i<=n;i++){
        dist[i] = map[1][i];
    }

    isvisitd[1] = true;//标记1已被访问  从1开始

    //找到权值最小点并记下位置
    for(i = 1;i<n;i++){
            min = MAX;
            for(j = 1;j<=n;j++){
            if(!isvisitd[j]&&dist[j]<min){
                min = dist[j];
                pos = j;//记录下该位置
            }
        }

        sum+=min;
        isvisitd[pos] = true;

        //更新权值
        for(j = 1;j<=n;j++)    {
            if(!isvisitd[j]&&dist[j]>map[pos][j]){
                dist[j] = map[pos][j];
            }
        }

    }
    return sum;
}
int main(){
    int i,j,n,m,len;
    char start,end;
    while(scanf("%d",&n)!=EOF){
        if(n==0){
            break;
        }

        init(n);//初始化

        for(i=0;i<n-1;i++){
            cin>>start>>m;
            for( j = 0;j<m;j++){
                cin>>end>>len;
                map[i+1][end-'A'+1] = len;
                map[end-'A'+1][i+1] = len;
            }
        }
        cout<<prim(n)<<endl;
    }
    return 0;

}
运行结果如下：
 
 

最小生成树 Prim算法的实现及应用关于prim算法
先把有的点放于一个集合（或者数组）里，这个集合里存放的是所有走过的点。初始值为0或者false表示还没有点
声明一个一维数组用于记录各点的权值[可理解为起始点到目标点的距离]，
声明一个二维数组用于记录某点到某一点的权值，如果这两点不可达到，则设置为无穷大
具体执行过程：
先从某一点开始，把这一个开始的点放于声明的一个数组或者集合里，表明这一点已经被访问过。然后再从余下的n-1个点里去找那个权值最小的点并记录该点的位置然后再加上这一点的权值，同时将该点放于集合里表明该点已初访问。再更新权值
再看下图，从下图分析：
1、
先选取一个点作起始点，然后选择它邻近的权值最小的点（如果有多个与其相连的相同最小权值的点，随便选取一个）。如1作为起点。
isvisited[1]=1;   //表明把1加进来说明是已经访问过
pos=1; //记录该位置
//用dist[]数组不断刷新最小权值，dist[i](0<i<=点数)的值为：i点到邻近点（未被标记）的最小距离。
dist[1]=0;  //起始点i到邻近点的最小距离为0
dist[2]=map[pos][2]=4;
dist[3]=map[pos][3]=2;
dist[4]==map[pos][4]=3;
dist[5]=map[pos][5]=MaxInt;  //无法直达
dist[6]=map[pos][6]=MaxInt;
 
2、
再在伸延的点找与它邻近的两者权值最小的点。
//dist[]以3作当前位置进行更新
isvisited[3]=1;
pos=3;
dist[1]=0;   //已标记，不更新
dist[2]=map[pos][2]=4;  //比5小，不更新
dist[3]=2;  //已标记，不更新
dist[4]=map[pos][4]=3;   //比1大，更新
dist[5]=map[pos][5]=MaxInt;
dist[6]=map[pos][6]=MaxInt;
 
3、最后的结果:
 
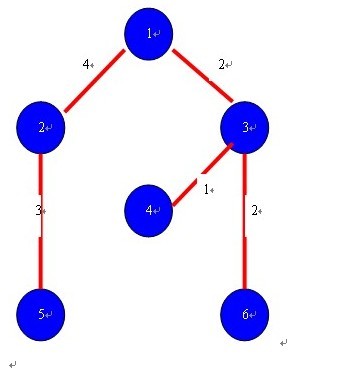
当所有点都连同后，结果最生成树如上图所示。
所有权值相加就是最小生成树，其值为2+1+2+4+3=12。
prim算法的实现：
[cpp] view plain copy
//prim算法  
  
int prim(int n){  
  
         int i,j,min,pos;  
  
         int sum=0;  
  
         memset(isvisited,false,sizeof(isvisited));  
  
   
  
         //初始化  
  
         for(i=1;i<=n;i++){  
  
                   dist[i]=map[1][i];  
  
         }  
  
   
  
         //从1开始  
  
         isvisited[1]=true;  
  
         dist[1]=MAX;  
  
   
  
         //找到权值最小点并记录下位置  
  
         for(i=1;i<n;i++){  
  
                   min=MAX;  
  
                   //pos=-1;  
  
                   for(j=1;j<=n;j++){  
  
                            if(!isvisited[j] && dist[j]<min){  
  
                                     min=dist[j];  
  
                                     pos=j;  
  
                            }  
  
                   }          
  
                   sum+=dist[pos];//加上权值  
  
                   isvisited[pos]=true;  
  
   
  
                   //更新权值  
  
                   for(j=1;j<=n;j++){  
  
                            if(!isvisited[j] && dist[j]>map[pos][j]){  
  
                                     dist[j]=map[pos][j];  
  
                            }  
  
                   }  
  
         }          
  
         return sum;  
  
}  
  
   
算法的应用：
应用上面的这个模板基本上能解决一些常见的最小生成树的算法，例如像杭电上的ACM题目：
题目链接地址：
HDOJ1863：http://acm.hdu.edu.cn/showproblem.php?pid=1863
HDOJ1875：http://acm.hdu.edu.cn/showproblem.php?pid=1875
HDOJ1879：http://acm.hdu.edu.cn/showproblem.php?pid=1879
HDOJ1233：http://acm.hdu.edu.cn/showproblem.php?pid=1233
HDOJ1162：http://acm.hdu.edu.cn/showproblem.php?pid=1162
HDOJ1301：http://acm.hdu.edu.cn/showproblem.php?pid=1301
 

posted on 2018-02-24 10:53 AlanTu 阅读(29015) 评论(2) 编辑收藏举报

刷新页面返回顶部

AlanTu

prim算法

Jungle Roads

最小生成树 Prim算法的实现及应用

导航

公告