TF-IDF与余弦相似性的应用
TF-IDF与余弦相似性的应用(一):自动提取关键词
这个标题看上去好像很复杂,其实我要谈的是一个很简单的问题。
有一篇很长的文章,我要用计算机提取它的关键词(Automatic Keyphrase extraction),完全不加以人工干预,请问怎样才能正确做到?

这个问题涉及到数据挖掘、文本处理、信息检索等很多计算机前沿领域,但是出乎意料的是,有一个非常简单的经典算法,可以给出令人相当满意的结果。它简单到都不需要高等数学,普通人只用10分钟就可以理解,这就是我今天想要介绍的TF-IDF算法。
让我们从一个实例开始讲起。假定现在有一篇长文《中国的蜜蜂养殖》,我们准备用计算机提取它的关键词。

一个容易想到的思路,就是找到出现次数最多的词。如果某个词很重要,它应该在这篇文章中多次出现。于是,我们进行"词频"(Term Frequency,缩写为TF)统计。
结果你肯定猜到了,出现次数最多的词是----"的"、"是"、"在"----这一类最常用的词。它们叫做"停用词"(stop words),表示对找到结果毫无帮助、必须过滤掉的词。
假设我们把它们都过滤掉了,只考虑剩下的有实际意义的词。这样又会遇到了另一个问题,我们可能发现"中国"、"蜜蜂"、"养殖"这三个词的出现次数一样多。这是不是意味着,作为关键词,它们的重要性是一样的?
显然不是这样。因为"中国"是很常见的词,相对而言,"蜜蜂"和"养殖"不那么常见。如果这三个词在一篇文章的出现次数一样多,有理由认为,"蜜蜂"和"养殖"的重要程度要大于"中国",也就是说,在关键词排序上面,"蜜蜂"和"养殖"应该排在"中国"的前面。
所以,我们需要一个重要性调整系数,衡量一个词是不是常见词。如果某个词比较少见,但是它在这篇文章中多次出现,那么它很可能就反映了这篇文章的特性,正是我们所需要的关键词。
用统计学语言表达,就是在词频的基础上,要对每个词分配一个"重要性"权重。最常见的词("的"、"是"、"在")给予最小的权重,较常见的词("中国")给予较小的权重,较少见的词("蜜蜂"、"养殖")给予较大的权重。这个权重叫做"逆文档频率"(Inverse Document Frequency,缩写为IDF),它的大小与一个词的常见程度成反比。
知道了"词频"(TF)和"逆文档频率"(IDF)以后,将这两个值相乘,就得到了一个词的TF-IDF值。某个词对文章的重要性越高,它的TF-IDF值就越大。所以,排在最前面的几个词,就是这篇文章的关键词。
下面就是这个算法的细节。
第一步,计算词频。

考虑到文章有长短之分,为了便于不同文章的比较,进行"词频"标准化。

或者

第二步,计算逆文档频率。
这时,需要一个语料库(corpus),用来模拟语言的使用环境。
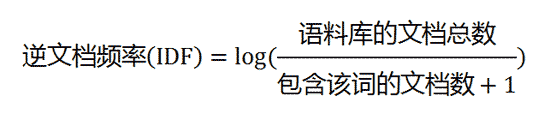
如果一个词越常见,那么分母就越大,逆文档频率就越小越接近0。分母之所以要加1,是为了避免分母为0(即所有文档都不包含该词)。log表示对得到的值取对数。
第三步,计算TF-IDF。
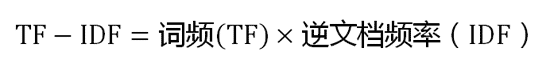
可以看到,TF-IDF与一个词在文档中的出现次数成正比,与该词在整个语言中的出现次数成反比。所以,自动提取关键词的算法就很清楚了,就是计算出文档的每个词的TF-IDF值,然后按降序排列,取排在最前面的几个词。
还是以《中国的蜜蜂养殖》为例,假定该文长度为1000个词,"中国"、"蜜蜂"、"养殖"各出现20次,则这三个词的"词频"(TF)都为0.02。然后,搜索Google发现,包含"的"字的网页共有250亿张,假定这就是中文网页总数。包含"中国"的网页共有62.3亿张,包含"蜜蜂"的网页为0.484亿张,包含"养殖"的网页为0.973亿张。则它们的逆文档频率(IDF)和TF-IDF如下:
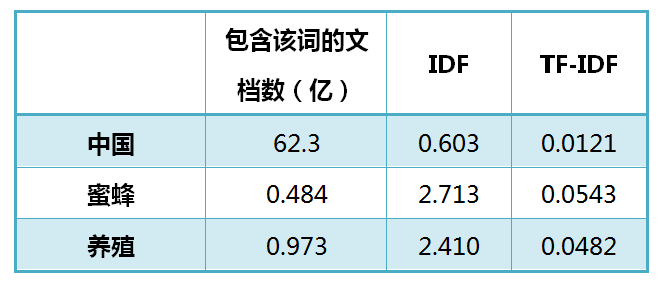
从上表可见,"蜜蜂"的TF-IDF值最高,"养殖"其次,"中国"最低。(如果还计算"的"字的TF-IDF,那将是一个极其接近0的值。)所以,如果只选择一个词,"蜜蜂"就是这篇文章的关键词。
除了自动提取关键词,TF-IDF算法还可以用于许多别的地方。比如,信息检索时,对于每个文档,都可以分别计算一组搜索词("中国"、"蜜蜂"、"养殖")的TF-IDF,将它们相加,就可以得到整个文档的TF-IDF。这个值最高的文档就是与搜索词最相关的文档。
TF-IDF算法的优点是简单快速,结果比较符合实际情况。缺点是,单纯以"词频"衡量一个词的重要性,不够全面,有时重要的词可能出现次数并不多。而且,这种算法无法体现词的位置信息,出现位置靠前的词与出现位置靠后的词,都被视为重要性相同,这是不正确的。(一种解决方法是,对全文的第一段和每一段的第一句话,给予较大的权重。)
TF-IDF与余弦相似性的应用(二):找出相似文章
今天,我们再来研究另一个相关的问题。有些时候,除了找到关键词,我们还希望找到与原文章相似的其他文章。比如,"Google新闻"在主新闻下方,还提供多条相似的新闻。

为了找出相似的文章,需要用到"余弦相似性"(cosine similiarity)。下面,我举一个例子来说明,什么是"余弦相似性"。
为了简单起见,我们先从句子着手。
句子A:我喜欢看电视,不喜欢看电影。
句子B:我不喜欢看电视,也不喜欢看电影。
请问怎样才能计算上面两句话的相似程度?
基本思路是:如果这两句话的用词越相似,它们的内容就应该越相似。因此,可以从词频入手,计算它们的相似程度。
第一步,分词。
句子A:我/喜欢/看/电视,不/喜欢/看/电影。
句子B:我/不/喜欢/看/电视,也/不/喜欢/看/电影。
第二步,列出所有的词。
我,喜欢,看,电视,电影,不,也。
第三步,计算词频。
句子A:我 1,喜欢 2,看 2,电视 1,电影 1,不 1,也 0。
句子B:我 1,喜欢 2,看 2,电视 1,电影 1,不 2,也 1。
第四步,写出词频向量。
句子A:[1, 2, 2, 1, 1, 1, 0]
句子B:[1, 2, 2, 1, 1, 2, 1]
到这里,问题就变成了如何计算这两个向量的相似程度。
我们可以把它们想象成空间中的两条线段,都是从原点([0, 0, ...])出发,指向不同的方向。两条线段之间形成一个夹角,如果夹角为0度,意味着方向相同、线段重合;如果夹角为90度,意味着形成直角,方向完全不相似;如果夹角为180度,意味着方向正好相反。因此,我们可以通过夹角的大小,来判断向量的相似程度。夹角越小,就代表越相似。
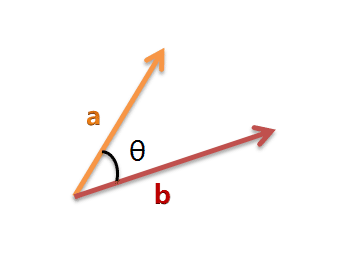
以二维空间为例,上图的a和b是两个向量,我们要计算它们的夹角θ。余弦定理告诉我们,可以用下面的公式求得:
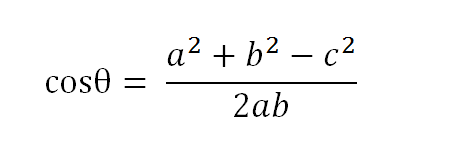
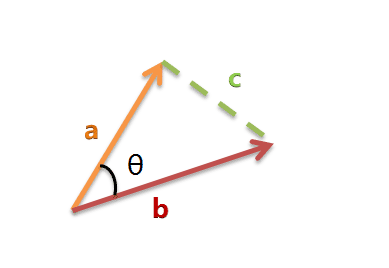
假定a向量是[x1, y1],b向量是[x2, y2],那么可以将余弦定理改写成下面的形式:
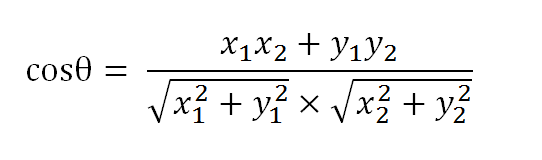
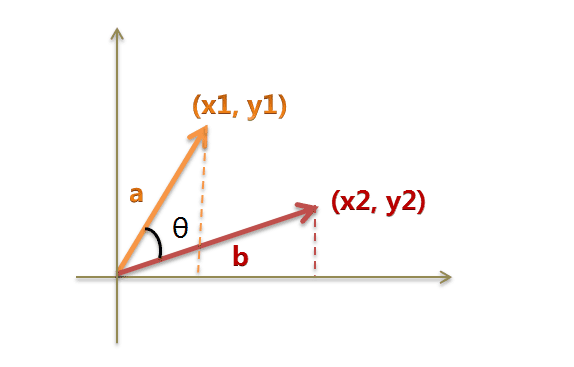
数学家已经证明,余弦的这种计算方法对n维向量也成立。假定A和B是两个n维向量,A是 [A1, A2, ..., An] ,B是 [B1, B2, ..., Bn] ,则A与B的夹角θ的余弦等于:
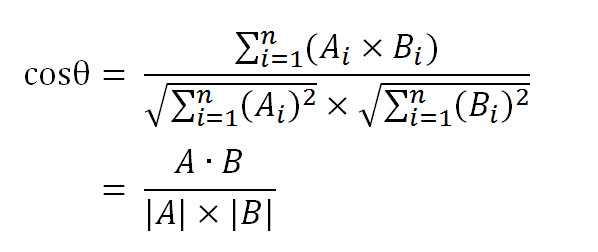
使用这个公式,我们就可以得到,句子A与句子B的夹角的余弦。
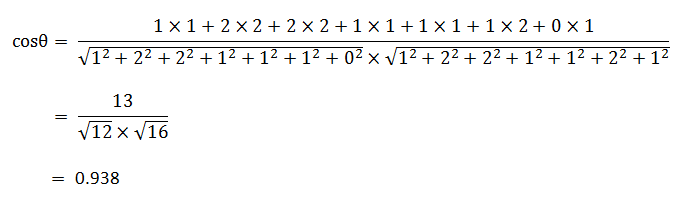
余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似,这就叫"余弦相似性"。所以,上面的句子A和句子B是很相似的,事实上它们的夹角大约为20.3度。
由此,我们就得到了"找出相似文章"的一种算法:
(1)使用TF-IDF算法,找出两篇文章的关键词;
(2)每篇文章各取出若干个关键词(比如20个),合并成一个集合,计算每篇文章对于这个集合中的词的词频(为了避免文章长度的差异,可以使用相对词频);
(3)生成两篇文章各自的词频向量;
(4)计算两个向量的余弦相似度,值越大就表示越相似。
"余弦相似度"是一种非常有用的算法,只要是计算两个向量的相似程度,都可以采用它。
下一次,我想谈谈如何在词频统计的基础上,自动生成一篇文章的摘要。




