贪心算法 - 0/1背包问题

1、问题描述：

     给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问:应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

     形式化描述：给定c >0, wi >0, vi >0 , 1≤i≤n.要求找一n元向量(x1,x2,…,xn,), xi∈{0,1}, ∋ ∑ wi xi≤c,且∑ vi xi达最大.即一个特殊的整数规划问题。

       2、最优性原理：

     设(y1,y2,…,yn)是 (3.4.1)的一个最优解.则(y2,…,yn)是下面相应子问题的一个最优解:

     证明:使用反证法。若不然,设(z2,z3,…,zn)是上述子问题的一个最优解,而(y2,y3,…,yn)不是它的最优解。显然有
                                    ∑vizi > ∑viyi   (i=2,…,n)
     且                           w1y1+ ∑wizi<= c
     因此                       v1y1+ ∑vizi (i=2,…,n) > ∑ viyi, (i=1,…,n) 
     说明(y1,z2, z3,…,zn)是(3.4.1)0-1背包问题的一个更优解,导出(y1,y2,…,yn)不是背包问题的最优解,矛盾。

       3、递推关系：

    设所给0-1背包问题的子问题

     

     的最优值为m(i，j)，即m(i，j)是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值。由0-1背包问题的最优子结构性质，可以建立计算m(i，j)的递归式:

     注:(3.4.3)式此时背包容量为j，可选择物品为i。此时在对xi作出决策之后,问题处于两种状态之一:
    (1)背包剩余容量是j,没产生任何效益；
    (2)剩余容量j-wi,效益值增长了vi ；
     使用递归C++代码如下：

　　

#include<iostream>
using namespace std;

const int N=3;
const int W=50;
int weights[N+1]={0,10,20,30};
int values[N+1]={0,60,100,120};
int V[N+1][W+1]={0};

int knapsack(int i,int j)
{
    int value;
    if(V[i][j]<0)
    {
        if(j<weights[i])
        {
            value=knapsack(i-1,j);
        }
        else
        {
            value=max(knapsack(i-1,j),values[i]+knapsack(i-1,j-weights[i]));
        }
        V[i][j]=value;
    }
    return V[i][j];
}

int main()
{
    int i,j;
    for(i=1;i<=N;i++)
        for(j=1;j<=W;j++)
            V[i][j]=-1;
    cout<<knapsack(3,50)<<endl;
    cout<<endl;
}

不使用递归的C++代码：简单一点的修改http://www.cppblog.com/Geek/archive/2009/12/02/102393.html

//3d10-1 动态规划 背包问题
#include <iostream>
using namespace std;

const int N = 4;

void Knapsack(int v[],int w[],int c,int n,int m[][10]);
void Traceback(int m[][10],int w[],int c,int n,int x[]);

int main()
{
    int c=8;
    int v[]={0,2,1,4,3},w[]={0,1,4,2,3};//下标从1开始
    int x[N+1];
    int m[10][10];

    cout<<"待装物品重量分别为："<<endl;
    for(int i=1; i<=N; i++)
    {
        cout<<w[i]<<" ";
    }
    cout<<endl;

    cout<<"待装物品价值分别为："<<endl;
    for(int i=1; i<=N; i++)
    {
        cout<<v[i]<<" ";
    }
    cout<<endl;

    Knapsack(v,w,c,N,m);

    cout<<"背包能装的最大价值为："<<m[1][c]<<endl;

    Traceback(m,w,c,N,x);
    cout<<"背包装下的物品编号为："<<endl;
    for(int i=1; i<=N; i++)
    {
        if(x[i]==1)
        {
            cout<<i<<" ";
        }
    }
    cout<<endl;

    return 0;
}

void Knapsack(int v[],int w[],int c,int n,int m[][10])
{
    int jMax = min(w[n]-1,c);//背包剩余容量上限 范围[0~w[n]-1]
    for(int j=0; j<=jMax;j++)
    {
        m[n][j]=0;
    }

    for(int j=w[n]; j<=c; j++)//限制范围[w[n]~c]
    {
        m[n][j] = v[n];
    }

    for(int i=n-1; i>1; i--)
    {
        jMax = min(w[i]-1,c);
        for(int j=0; j<=jMax; j++)//背包不同剩余容量j<=jMax<c
        {
            m[i][j] = m[i+1][j];//没产生任何效益
        }

        for(int j=w[i]; j<=c; j++) //背包不同剩余容量j-wi >c
        {
            m[i][j] = max(m[i+1][j],m[i+1][j-w[i]]+v[i]);//效益值增长vi
        }
    }
    m[1][c] = m[2][c];
    if(c>=w[1])
    {
        m[1][c] = max(m[1][c],m[2][c-w[1]]+v[1]);
    }
}

//x[]数组存储对应物品0-1向量,0不装入背包，1表示装入背包
void Traceback(int m[][10],int w[],int c,int n,int x[])
{
    for(int i=1; i<n; i++)
    {
        if(m[i][c] == m[i+1][c])
        {
            x[i]=0;
        }
        else
        {
            x[i]=1;
            c-=w[i];
        }
    }
    x[n]=(m[n][c])?1:0;
}

运行结果：

 

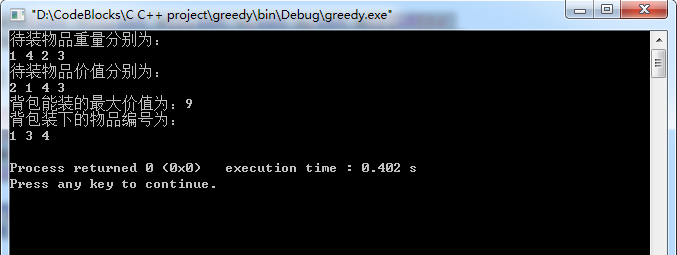
算法执行过程对m[][]填表及Traceback回溯过程如图所示：

      从m(i，j)的递归式容易看出，算法Knapsack需要O(nc)计算时间; Traceback需O(n)计算时间；算法总体需要O(nc)计算时间。当背包容量c很大时，算法需要的计算时间较多。例如，当c>2^n时，算法需要Ω(n2^n)计算时间。