动态规划 - 最优二叉搜索树
二叉查找树
摘要:
本章介绍了二叉查找树的概念及操作。主要内容包括二叉查找树的性质,如何在二叉查找树中查找最大值、最小值和给定的值,如何找出某一个元素的前驱和后继,如何在二叉查找树中进行插入和删除操作。在二叉查找树上执行这些基本操作的时间与树的高度成正比,一棵随机构造的二叉查找树的期望高度为O(lgn),从而基本动态集合的操作平均时间为θ(lgn)。
1、二叉查找树
二叉查找树是按照二叉树结构来组织的,因此可以用二叉链表结构表示。二叉查找树中的关键字的存储方式满足的特征是:设x为二叉查找树中的一个结点。如果y是x的左子树中的一个结点,则key[y]≤key[x]。如果y是x的右子树中的一个结点,则key[x]≤key[y]。根据二叉查找树的特征可知,采用中根遍历一棵二叉查找树,可以得到树中关键字有小到大的序列。http://www.cnblogs.com/Anker/archive/2013/01/27/2878594.html介绍了二叉树概念及其遍历。一棵二叉树查找及其中根遍历结果如下图所示:
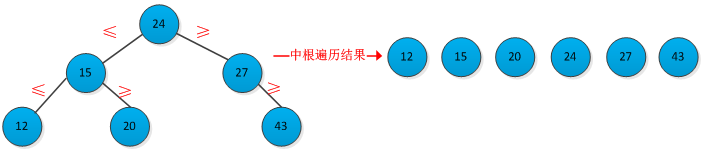
书中给出了一个定理:如果x是一棵包含n个结点的子树的根,则其中根遍历运行时间为θ(n)。
问题:二叉查找树性质与最小堆之间有什么区别?能否利用最小堆的性质在O(n)时间内,按序输出含有n个结点的树中的所有关键字?
2、查询二叉查找树
二叉查找树中最常见的操作是查找树中的某个关键字,除了基本的查询,还支持最大值、最小值、前驱和后继查询操作,书中就每种查询进行了详细的讲解。
(1)查找SEARCH
在二叉查找树中查找一个给定的关键字k的过程与二分查找很类似,根据二叉查找树在的关键字存放的特征,很容易得出查找过程:首先是关键字k与树根的关键字进行比较,如果k大比根的关键字大,则在根的右子树中查找,否则在根的左子树中查找,重复此过程,直到找到与遇到空结点为止。例如下图所示的查找关键字13的过程:(查找过程每次在左右子树中做出选择,减少一半的工作量)
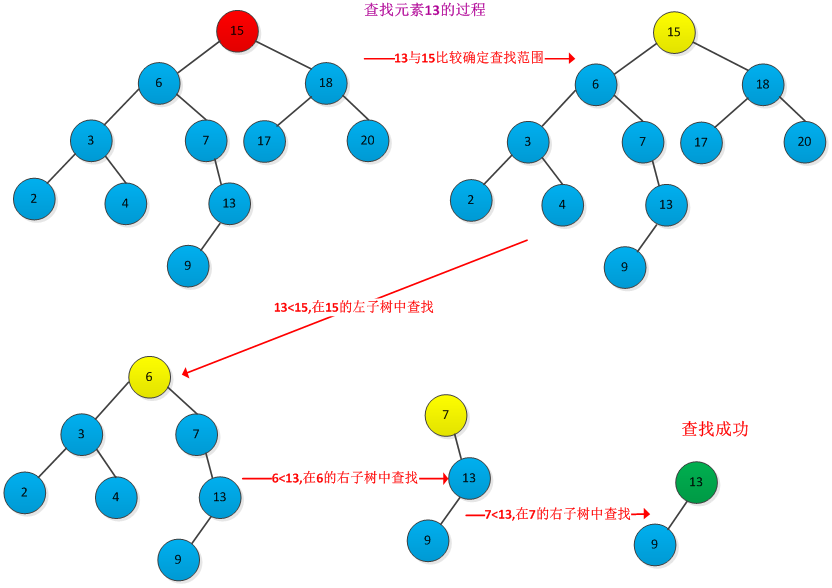
书中给出了查找过程的递归和非递归形式的伪代码:
1 TREE_SEARCH(x,k)
2 if x=NULL or k=key[x]
3 then return x
4 if(k<key[x])
5 then return TREE_SEARCH(left[x],k)
6 else
7 then return TREE_SEARCH(right[x],k)
1 ITERATIVE_TREE_SEARCH(x,k)
2 while x!=NULL and k!=key[x]
3 do if k<key[x]
4 then x=left[x]
5 else
6 then x=right[x]
7 return x
(2)查找最大关键字和最小关键字
根据二叉查找树的特征,很容易查找出最大和最小关键字。查找二叉树中的最小关键字:从根结点开始,沿着各个节点的left指针查找下去,直到遇到NULL时结束。如果一个结点x无左子树,则以x为根的子树中,最小关键字就是key[x]。查找二叉树中的最大关键字:从根结点开始,沿着各个结点的right指针查找下去,直到遇到NULL时结束。书中给出了查找最大最小关键字的伪代码:
1 TREE_MINMUM(x)
2 while left[x] != NULL
3 do x=left[x]
4 return x
1 1 TREE_MAXMUM(x)
2 2 while right[x] != NULL
3 3 do x= right[x]
4 4 return x
(3)前驱和后继
给定一个二叉查找树中的结点,找出在中序遍历顺序下某个节点的前驱和后继。如果树中所有关键字都不相同,则某一结点x的前驱就是小于key[x]的所有关键字中最大的那个结点,后继即是大于key[x]中的所有关键字中最小的那个结点。根据二叉查找树的结构和性质,不用对关键字做任何比较,就可以找到某个结点的前驱和后继。
查找前驱步骤:先判断x是否有左子树,如果有则在left[x]中查找关键字最大的结点,即是x的前驱。如果没有左子树,则从x继续向上执行此操作,直到遇到某个结点是其父节点的右孩子结点。例如下图查找结点7的前驱结点6过程: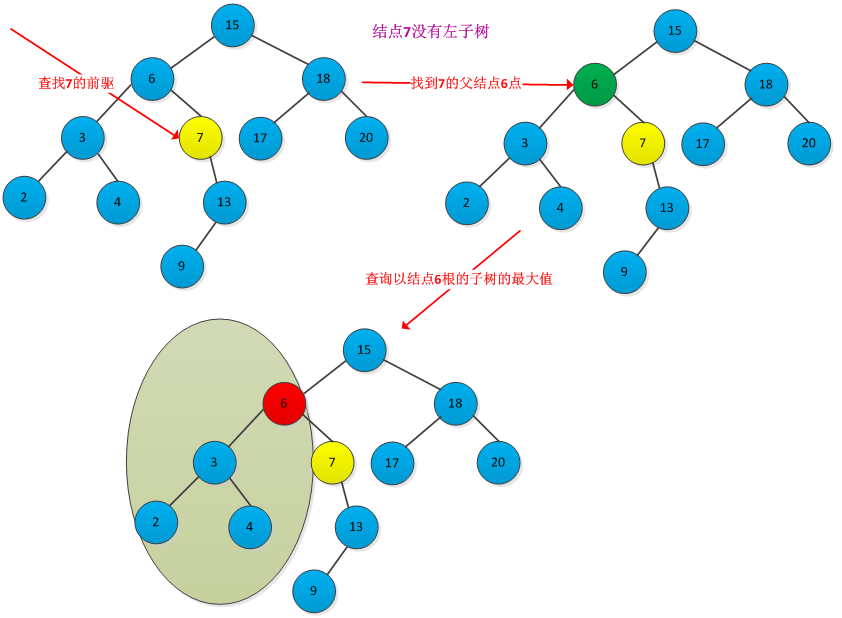
查找后继步骤:先判断x是否有右子树,如果有则在right[x]中查找关键字最小的结点,即使x的后继。如果没有右子树,则从x的父节点开始向上查找,直到遇到某个结点是其父结点的左儿子的结点时为止。例如下图查找结点13的后继结点15的过程: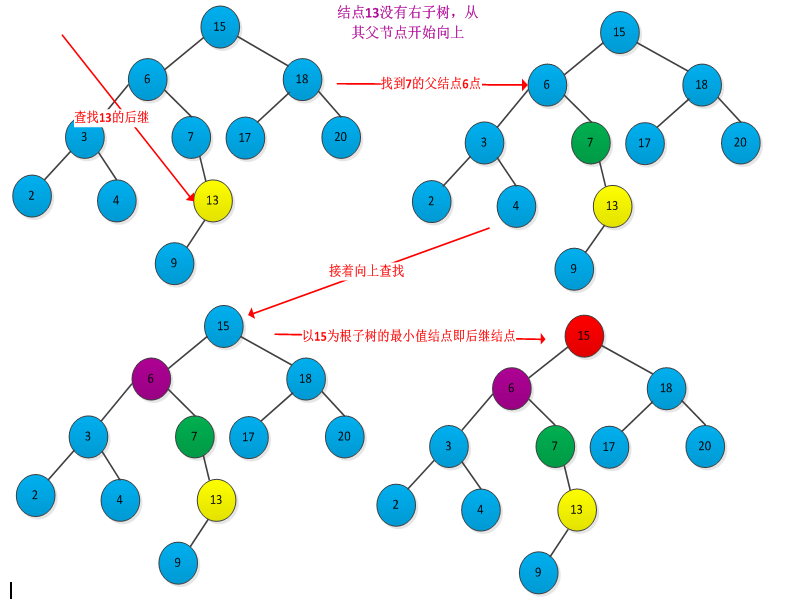
书中给出了求x结点后继结点的伪代码:
1 TREE_PROCESSOR(x)
2 if right[x] != NULL
3 then return TREE_MINMUM(right(x))
4 y=parent[x]
5 while y!= NULL and x ==right[y]
6 do x = y
7 y=parent[y]
8 return y
定理:对一棵高度为h的二叉查找,动态集合操作SEARCH、MINMUM、MAXMUM、SUCCESSOR、PROCESSOR等的运行时间均为O(h)。
3、插入和删除
插入和删除会引起二叉查找表示的动态集合的变化,难点在在插入和删除的过程中要保持二叉查找树的性质。插入过程相当来说要简单一些,删除结点比较复杂。
(1)插入
插入结点的位置对应着查找过程中查找不成功时候的结点位置,因此需要从根结点开始查找带插入结点位置,找到位置后插入即可。下图所示插入结点过程:
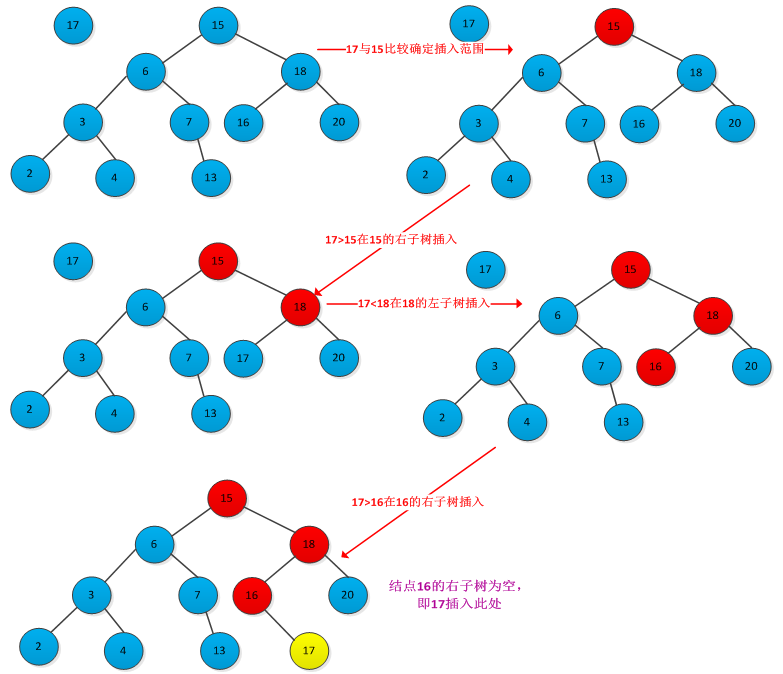
书中给出了插入过程的伪代码:
1 TREE_INSERT(T,z)
2 y = NULL;
3 x =root[T]
4 while x != NULL
5 do y =x
6 if key[z] < key[x]
7 then x=left[x]
8 else x=right[x]
9 parent[z] =y
10 if y=NULL
11 then root[T] =z
12 else if key[z]>key[y]
13 then keft[y] = z
14 else right[y] =z
插入过程运行时间为O(h),h为树的高度。
(2)删除
从二叉查找树中删除给定的结点z,分三种情况讨论:
<1>结点z没有左右子树,则修改其父节点p[z],使其为NULL。删除过程如下图所示: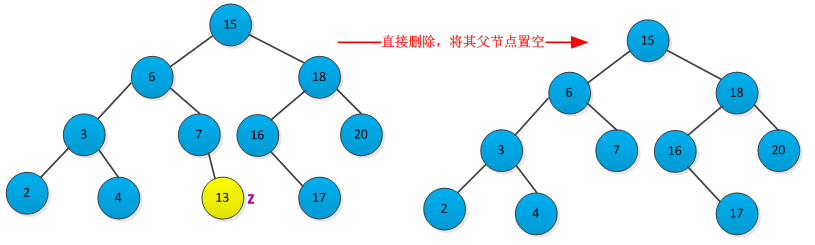
<2>如果结点z只有一个子树(左子树或者右子树),通过在其子结点与父节点建立一条链来删除z。删除过程如下图所示: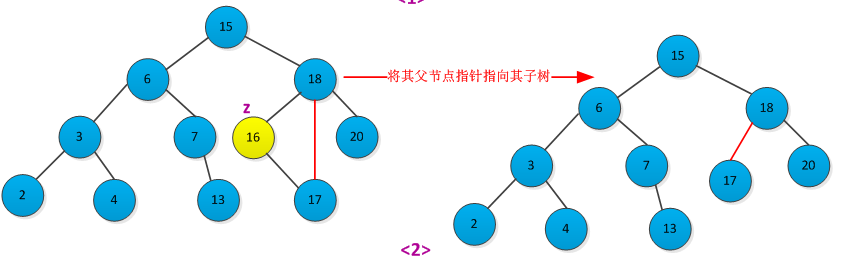
<3>如果z有两个子女,则先删除z的后继y(y没有左孩子),在用y的内容来替代z的内容。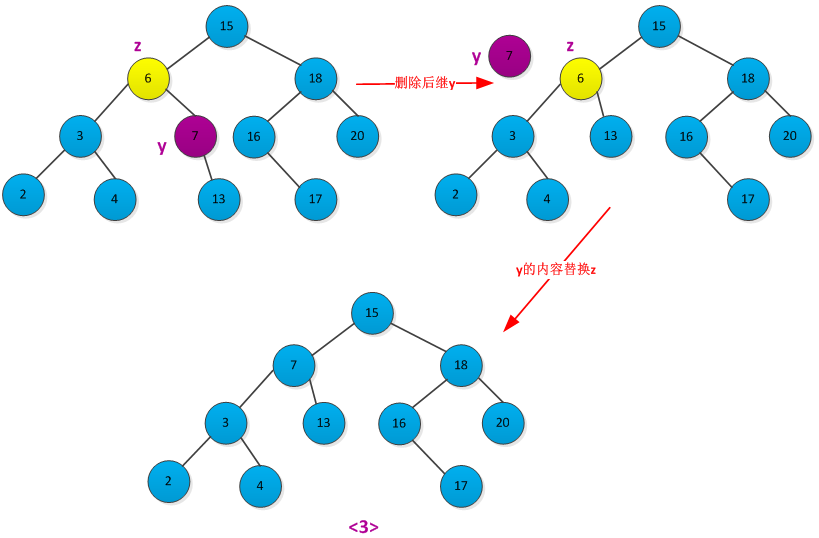
书中给出了删除过程的伪代码:
1 TREE_DELETE(T,z)
2 if left[z] ==NULL or right[z] == NULL
3 then y=z
4 else y=TREE_SUCCESSOR(z)
5 if left[y] != NULL
6 then x=left[y]
7 else x=right[y]
8 if x!= NULL
9 then parent[x] = parent[y]
10 if p[y] ==NULL
11 then root[T] =x
12 else if y = left[[prarnt[y]]
13 then left[parent[y]] = x
14 else right[parent[y]] =x
15 if y!=z
16 then key[z] = key[y]
17 copy y's data into z
18 return y
定理:对高度为h的二叉查找树,动态集合操作INSERT和DELETE的运行时间为O(h)。
4、实现测试
采用C++语言实现一个简单的二叉查找树,支持动态集合的基本操作:search、minmum、maxmum、predecessor、successor、insert和delete。设计的二叉查找树结构如下所示:
1 template <class T>
2 class BinarySearchTreeNode
3 {
4 public:
5 T elem;
6 struct BinarySearchTreeNode<T> *parent;
7 struct BinarySearchTreeNode<T>* left;
8 struct BinarySearchTreeNode<T>* right;
9 };
10
11 template <class T>
12 class BinarySearchTree
13 {
14 public:
15 BinarySearchTree();
16 void tree_insert(const T& elem);
17 int tree_remove(const T& elem );
18 BinarySearchTreeNode<T>* tree_search(const T& elem)const;
19 T tree_minmum(BinarySearchTreeNode<T>* root)const;
20 T tree_maxmum(BinarySearchTreeNode<T>* root)const;
21 T tree_successor(const T& elem) const;
22 T tree_predecessor(const T& elem)const;
23 int empty() const;
24 void inorder_tree_walk()const;
25 BinarySearchTreeNode<T>* get_root()const {return root;}
26 private:
27 BinarySearchTreeNode<T>* root;
28 };
完整程序如下所示:
 View Code
View Code 程序测试结果如下所示:
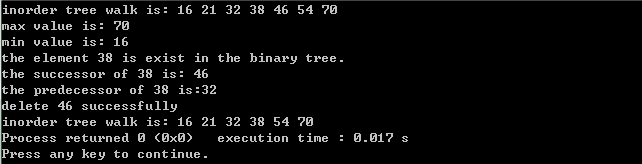
二叉树实现时候添加了一个父结点指针,方便寻找给定结点的前驱和后继。二叉树中删除操作实现比较复杂,需要分类讨论,我分三种情况进行讨论,程序写的有些繁琐,可以进行优化。优化后的代码如下:
1 template <class T>
2 int BinarySearchTree<T>::tree_delete(const T& elem)
3 {
4 //找到该元素对应的结点
5 BinarySearchTreeNode<T>* pnode = tree_search(elem);
6 if(NULL != pnode)
7 {
8 BinarySearchTreeNode<T> *qnode,*tnode;
9 //判断结点是否有左右孩子
10 if(pnode->left == NULL || pnode->right == NULL)
11 qnode = pnode; //有一个左孩子或者一个右孩子和没有左右孩子
12 else
13 qnode = tree_search(tree_successor(elem)); //有左右孩子
14 if(NULL != qnode->left)
15 tnode = qnode->left;
16 else
17 tnode = qnode->right;
18 if(NULL != tnode)
19 tnode->parent = qnode->parent;
20 if(qnode->parent == NULL)
21 root = tnode;
22 else
23 if(qnode == qnode->parent->left)
24 qnode->parent->left = tnode;
25 else
26 qnode->parent->right = tnode;
27 if(qnode != pnode)
28 pnode->elem = qnode->elem; //将后继结点的值复制到要删除的结点的值
29 delete qnode;
30 return 0;
31 }
32 return -1;
33 }
5、随机构造二叉查找树
二叉查找上各种基本操作的运行时间都是O(h),h为树的高度。但是在元素插入和删除过程中,树的高度会发生改变。如果n个元素按照严格增长的顺序插入,那个构造出的二叉查找树的高度为n-1。例如按照先后顺序插入7、15、18、20、34、46、59元素构造二叉查找树,二叉查找树结构如下所示:
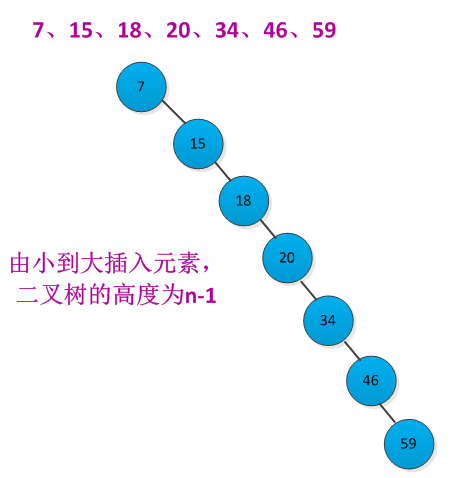
1、前言:
接着学习动态规划方法,最优二叉查找树问题。二叉查找树参考http://www.cnblogs.com/Anker/archive/2013/01/28/2880581.html。如果在二叉树中查找元素不考虑概率及查找不成功的情况下,可以采用红黑树或者平衡二叉树来搜索,这样可以在O(lgn)时间内完成。而现实生活中,查找的关键字是有一定的概率的,就是说有的关键字可能经常被搜索,而有的很少被搜索,而且搜索的关键字可能不存在,为此需要根据关键字出现的概率构建一个二叉树。比如中文输入法字库中各词条(单字、词组等)的先验概率,针对用户习惯可以自动调整词频——所谓动态调频、高频先现原则,以减少用户翻查次数,使得经常用的词汇被放置在前面,这样就能有效地加快查找速度。这就是最优二叉树所要解决的问题。
2、问题描述
给定一个由n个互异的关键字组成的有序序列K={k1<k2<k3<,……,<kn}和它们被查询的概率P={p1,p2,p3,……,pn},要求构造一棵二叉查找树T,使得查询所有元素的总的代价最小。对于一个搜索树,当搜索的元素在树内时,表示搜索成功。当不在树内时,表示搜索失败,用一个“虚叶子节点”来标示搜索失败的情况,因此需要n+1个虚叶子节点{d0<d1<……<dn},对于应di的概率序列是Q={q0,q1,……,qn}。其中d0表示搜索元素小于k1的失败结果,dn表示搜索元素大于kn的失败情况。di(0<i<n)表示搜索节点在ki和k(i+1)之间时的失败情况。因此有如下公式:

由每个关键字和每个虚拟键被搜索的概率,可以确定在一棵给定的二叉查找树T内一次搜索的期望代价。设一次搜索的实际代价为检查的节点个数,即在T内搜索所发现的节点的深度加上1。所以在T内一次搜索的期望代价为:
需要注意的是:一棵最优二叉查找树不一定是一棵整体高度最小的树,也不一定总是把最大概率的关键字放在根部。
(3)动态规划求解过程
1)最优二叉查找树的结构
如果一棵最优二叉查找树T有一棵包含关键字ki,……,kj的子树T',那么这棵子树T’对于对于关键字ki,……kj和虚拟键di-1,……,dj的子问题也必定是最优的。
2)一个递归解
定义e[i,j]为搜索一棵包含关键字ki,……,kj的最优二叉查找树的期望代价,则分类讨论如下:
当j=i-1时,说明此时只有虚拟键di-1,故e[i,i-1] = qi-1
当j≥i时,需要从ki,……,kj中选择一个跟kr,然后用关键字ki,……,kr-1来构造一棵最优二叉查找树作为左子树,用关键字kr+1,……,kj来构造一棵最优二叉查找树作为右子树。定义一棵有关键字ki,……,kj的子树,定义概率的总和为:

因此如果kr是一棵包含关键字ki,……,kj的最优子树的根,则有:


故e[i,j]重写为:
![]()
最终的递归式如下:
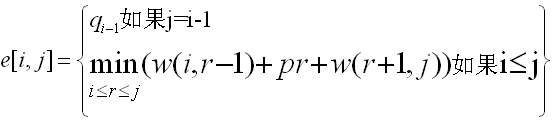
3)计算一棵最优二叉查找树的期望搜索代价
将e[i,j]的值保存到一个二维数组e[1..1+n,0..n]中,用root[i,j]来记录关键字ki,……,kj的子树的根,采用二维数组root[1..n,1..n]来表示。为了提高效率,防止重复计算,需要个二维数组w[1..n+1,0...n]来保存w(i,j)的值,其中w[i,j] = w[i,j-1]+pj+qj。数组给出了计算过程的伪代码:
OPTIMAL_BST(p,q,n)
for i=1 to n+1 //初始化e和w的值
do e[i,i-1] = qi-1;
w[i,i-1] = qi-1;
for l=1 to n
do for i=1 to n-l+1
do j=i+l-1;
e[i,j] = MAX;
w[i,j] = w[i,j-1]+pj+qj;
for r=i to j
do t=e[i,r-1]+e[r+1,j]+w[i,j]
if t<e[i,j]
then e[i,j] = t;
root[i,j] = r;
return e and root;
4)构造一棵最优二叉查找树
根据地第三步中得到的root表,可以递推出各个子树的根,从而可以构建出一棵最优二叉查找树。从root[1,n]开始向下递推,一次找出树根,及左子树和右子树。
4、编程实现
针对一个具体的实例编程实现,现在有5个关键字,其出现的概率P={0.15,0.10,0.05,0.10,0.20},查找虚拟键的概率q={0.05,0.10,0.05,0.05,0.05,0.10}。采用C++语言是实现如下:
#include<iostream>
using namespace std;
const int N=5;
const int MAX=9999999;
float p[N+1]={0,0.15,0.10,0.05,0.1,0.20};
float q[N+1]={0.05,0.10,0.05,0.05,0.05,0.10};
float e[N+2][N+1];
int root[N+1][N+1];
float w[N+2][N+1];
void optimal_bst_search_tree(float p[],float q[],int n)
{
int i;
for(i=1;i<=n+1;i++)
{
e[i][i-1]=q[i-1];
w[i][i-1]=q[i-1];
}
int l,j,r;
for(l=1;l<=n;l++)
{
for(i=1;i<=n-l+1;i++)
{
j=i+l-1;
e[i][j]=MAX;
w[i][j]=w[i][j-1]+p[j]+q[j];
for(r=i;r<=j;r++)
{
double t=e[i][r-1]+e[r+1][j]+w[i][j];
if(t<e[i][j])
{
e[i][j]=t;
root[i][j]=r;
}
}
}
}
}
void print_root()
{
int i,j;
cout<<"各子树的根:"<<endl;
for(i=1;i<=N;i++)
{
for(j=1;j<=N;j++)
cout<<root[i][j]<<" ";
cout<<endl;
}
}
void construct_optimal_bst(int i,int j)
{
if(i<=j)
{
int r=root[i][j];
cout<<r<<" ";
construct_optimal_bst(i,r-1);
construct_optimal_bst(r+1,j);
}
}
void print_bst(int i,int j)
{
if(i==1&&j==N)
cout<<"root is "<<root[i][j]<<endl;
if(i<j)
{
int r=root[i][j];
if(i!=r)
cout<<"left child root "<<root[i][r-1]<<endl;
print_bst(i,root[i][j]-1);
if(j!=r)
cout<<"right child root "<<root[r+1][j]<<endl;
print_bst(root[i][j]+1,j);
}
}
int main()
{
optimal_bst_search_tree(p,q,N);
print_root();
cout<<"构造的最优二叉树:"<<endl;
construct_optimal_bst(1,5);
cout<<endl;
print_bst(1,5);
}
运行结果:
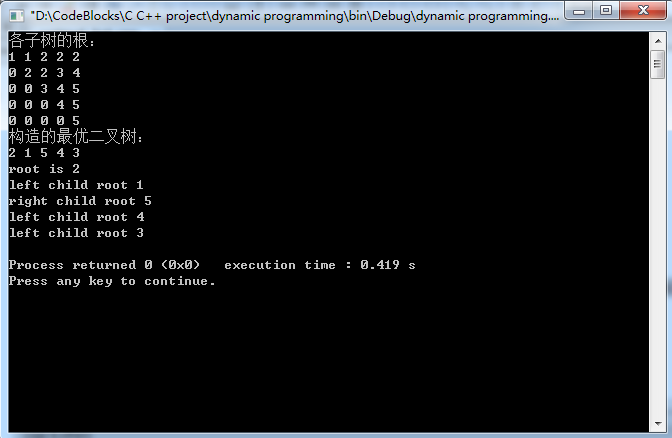




 浙公网安备 33010602011771号
浙公网安备 33010602011771号