快速排序
快速排序
对于n个数的输入数组来说,快速排序是一种最坏情况时间复杂度为O(n2)的排序算法,虽然最坏情况时间复杂度很差,但是快速排序通常是实际排序中最好的选择,因为它的平均性能非常好:它的期望时间复杂度是O(nlgn),而且O(nlgn)中隐含的常数因子非常小。
1、快速排序的描述
快速排序算法采用的分治算法,因此对一个子数组A[p…r]进行快速排序的三个步骤为:
(1)分解:数组A[p...r]被划分为两个(可能为空)子数组A[p...q-1]和A[q+1...r],给定一个枢轴,使得A[p...q-1]中的每个元素小于等于A[q],A[q+1...r]中的每个元素大于等于A[q],q下标是在划分过程中计算得出的。
(2)解决:通过递归调用快速排序,对子数组A[p...q-1]和A[q+1...r]进行排序。
(3)合并:因为两个子数组是就地排序,不需要合并操作,整个数组A[p…r]排序完成。
快速排序关键过程是对数组进行划分,划分过程需要选择一个主元素(pivot element)作为参照,围绕着这个主元素进划分子数组。举个列说明如何划分数组,现有子数组A={24,15,27,5,43,87,34},以最后一个元素为主元素进行划分,划分过程如图所示: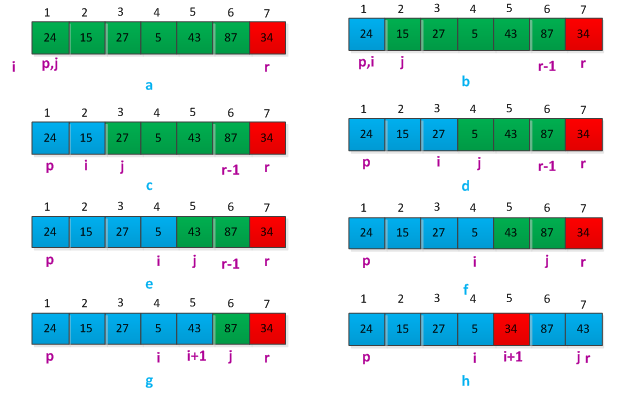
书中给出了划分过程的伪代码:
书中给出了划分过程的伪代码:
1 PARTITION(A,p,r) 2 x = A[r] //将最后一个元素作为主元素 3 i = p-1 4 for j=p to r-1 //从第一个元素开始到倒数第二个元素结束,比较确定主元的位置 5 do if A[j] <= x 6 i = i+1 7 exchange A[i] <-> A[j] 8 exchange A[i+1]<->A[r] //最终确定主元的位置 9 return i+1 //返回主元的位置
根据划分过程的为代码,书中又给出了快速排序的为代码:
1 QUICKSORT(A,p,r) 2 if p<r 3 q = PARTITION(A,p,r) //确定划分位置 4 QUICKSORT(A,p,q-1) //子数组A[p...q-1] 5 QUICKSORT(Q,q+1,r) //子数组A[q+1...r]
采用C++语言实现一个完成的快速排序程序,程序如下:
#include<iostream>using namespace std;void swap(int *a,int *b){ int temp=*a; *a=*b; *b=temp;}size_t Partition(int arr[],int p,int r){ int x=arr[r]; int i=p-1; int j; for(j=p;j<r;j++) { if(arr[j]<x) { i++; swap(&arr[i],&arr[j]); } } swap(&arr[i+1],&arr[r]); return (i+1);}void QuickSort(int arr[],int p,int r){ int q; if(p < r) { q = Partition(arr,p,r); QuickSort(arr,p,q-1); QuickSort(arr,q+1,r); }}int main(){ int arr[10]={19,88,3,5,7,39,79,37,8,9}; int i; QuickSort(arr,0,9); for(i=0;i<10;++i) cout<<arr[i]<<" "; return(0);}
划分数组时有另一种双向扫描的方法。
还是以最右边的元素作为基数。目的是左边的元素都是小于或等于基数,右边的元素都是大于基数的。先不管最右的数字,i从左往右扫描知道遇到一个不属于左边的数字,j从右往左扫描直到遇到一个不属于右边的数字,然后就可以交换i和j上的数字,那么这两个数字就放在了它们应该在的位置。然后i++,j–-再继续扫描,直到i和j相遇。最后要把最右边的基数和i上面的数字交换,i就是划分的结果。
代码如下:
#include <stdio.h>#include <stdlib.h>int partition(int arr[],int beg,int last);void quick_sort(int* datas,int beg,int last);void swap(int *a,int *b);int main(){ size_t i; int datas[10] = {78,13,9,23,45,14,35,65,56,79}; printf("After quick sort,the datas is:\n"); quick_sort(datas,0,9); for(i=0;i<10;++i) printf("%d ",datas[i]); exit(0);}void swap(int *a,int *b){ int temp = *a; *a = *b; *b = temp;}/*int partition(int a[], int l, int r){ int i = l, j = r - 1; while (i<=j) { while (i <= j && a[i] <= a[r]) i++; //左边元素<=基数 while (i <= j && a[j] > a[r]) j--; //右边元素 >基数 if (i >= j) break; swap(&a[i++], &a[j--]); } swap(&a[i], &a[r]); //i == j return i;}*/int partition(int arr[], int p, int r){ int i = p, j = r - 1; int key=arr[r]; while (i<=j) { while (i <= j && arr[i] <= key) i++; //左边元素<=基数 while (i <= j && arr[j] > key) j--; //右边元素 >基数 if(i<j) swap(&arr[i++], &arr[j--]); } swap(&arr[i], &arr[r]); //i == j return i;}void quick_sort(int* datas,int beg,int last){ int pivot; if(beg < last) { pivot = partition(datas,beg,last); quick_sort(datas,beg,pivot-1); quick_sort(datas,pivot+1,last); }}
挖坑填数+分治法的实现:
#include <stdio.h>#include <stdlib.h>int partition(int arr[],int beg,int last);void quick_sort(int* datas,int beg,int last);void swap(int *a,int *b);int main(){ size_t i; int datas[10] = {78,13,9,23,45,14,35,65,56,79}; printf("After quick sort,the datas is:\n"); quick_sort(datas,0,9); for(i=0;i<10;++i) printf("%d ",datas[i]); exit(0);}void swap(int *a,int *b){ int temp = *a; *a = *b; *b = temp;}/*int partition(int a[], int l, int r){ int i = l, j = r - 1; while (i<=j) { while (i <= j && a[i] <= a[r]) i++; //左边元素<=基数 while (i <= j && a[j] > a[r]) j--; //右边元素 >基数 if (i >= j) break; swap(&a[i++], &a[j--]); } swap(&a[i], &a[r]); //i == j return i;}*/int partition(int arr[], int p, int r){ int i = p, j = r; int key=arr[r]; while (i<j) { while (i <j && arr[i] <= key) i++; //左边元素<=基数 if(i<j) arr[j--]=arr[i]; while (i <j && arr[j] > key) j--; //右边元素 >基数 if(i<j) arr[i++]=arr[j]; } arr[i]=key; return i;}void quick_sort(int* datas,int beg,int last){ int pivot; if(beg < last) { pivot = partition(datas,beg,last); quick_sort(datas,beg,pivot-1); quick_sort(datas,pivot+1,last); }}主要注意上面3种方法的边界处理情况。。
2 快速排序的性能
快速排序的运行时间依赖于划分是否平衡,而平衡与否又依赖于用于划分的元素。如果划分是平衡的,那么快速排序算法性能和归并排序一样。如果划分是不平衡的,那么快速排序的性能就接近于插入排序了。
最坏情况划分
当划分产生的两个子问题分别包含了n-1个元素和0个元素时,快速排序的最坏情况发生了。
递归式子:
T(n)=T(n-1)+T(0)+O(n)
从直观上看,每一层递归的代价可以被累加起来,从而得到一个算术级数,其结果为O(n2)。
最好情况划分
在可能的最平衡的划分中,PARTITION得到的两个子问题的规模都不大于n/2.在这种情况下,算法运行时间的递归式为:
T(n)=2T(n/2)+O(n);
结果为T(n)=O(nlgn)。





