基本电路概念(二)什么是电容？

一、前言

我儿子对电路板有一种近乎疯狂的痴迷，每次周末加班的时候，他总是恳求我带他一起到公司，就是为了能够看一看电路板、看一看电路焊接过程。为了不影响工作，我只能是找一些废旧的电路板，加上从蜗窝同学那里搜刮来的电烙铁给小朋友进行电路焊接演示。废旧电路板上有不少的器件，于是问题少年的问题就来了，芯片里面有什么？电路板是几层的？电容的内部结构是什么？……于是乎钳子、起子、剪刀等工具不断的登场，我们家里就是一片狼籍，各种电子元件支离破碎……

其实打开一个普通的电解电容，里面的结构很简单，两个铝箔，一个绝缘纸卷在一起放到一个圆柱形的容器中，两个铝箔引出电容器的两个引脚。那么它的具体功能是什么呢？当然，给小朋友解释很简单：就是用来存储小电子的，不过作为工程师，我们当然不能那么肤浅，本文的主题就一个：详细描述电容的概念。

作为一个“数学控”，不拽上点数学总是觉得少了点什么。section 2描述了理解后续内容需要的数学基础，理解这个章节的内容需要单变量微积分和基本向量的知识。如果阅读者觉得痛苦，那么不要犹豫，直接跳过这个章节。section 3描述了一些物理学的基础，如果这也不是你的菜，那么我建议你记住计算平板电容之间电场的公式即可，其他的可以无视。section 4主要描述电容的概念，这是本文的核心内容。

二、数学基础

1、曲面积分（Surface Integral）

在什么是电压这篇文章中，我们描述了曲线积分，其实将曲线积分的概念推广到3维空间中就可以得到曲面积分的定义。曲面积分是积分的一种。和普通积分不一样的是：积分函数的取值沿的不是区间，而是特定的曲面，称为积分路径。对于曲面积分而言，被积函数可以是标量函数（标量场）或向量函数（向量场）。对于标量场，积分的值是路径各点上的函数值乘上相应的权重（一般是曲面面积）的黎曼和；对于矢量场，积分的值是路径各点上的函数值（该函数值是矢量）与曲面微元矢量的标量积（例如点积）的黎曼和。

标量场的曲面积分和本文的主题无关，因此我们举一个向量场的例子。考虑空间曲面Σ上的向量场，对于Σ上的每个点，是一个向量。想象一个穿过Σ的液体流，则曲面上的各点对应的矢量表示的流体的速度。则流量定义为单位时间穿过Σ的液体量。如果和Σ在每点相切，则流量为0，因为液体平行于Σ流动，从而不进不出。这也意味着如果既有切向分量也有法向分量，则只有法向分量对流量作出贡献。基于这个推理，要找出流量，我们必须取和Σ上每点的单位法向量的点积，公式如下：

流量

2、散度（Divergence）和通量（Flux）

是一个矢量场，在数学上，我们定义通过有向曲面的通量如下：

一般而言，面积是一个标量，但是在上面的公式中，面积是一个矢量，称为面积矢量（area vector）。该矢量的长度是面积的数值，其方向垂直与平面，用右手规则定义。就是面积矢量的微分。

散度是向量分析中的一个向量算子，将向量空间上的一个矢量场对应到一个标量场上。散度描述的是向量场里一个点是汇聚点还是发源点，形象地说，就是这包含这一点的一个微小体元中的向量是“向外”居多还是“向内”居多。我们定义向量场在x点的散度如下：

是x点附近的一个封闭曲面，这个封闭曲面的体积就是。

从定义中可以看出，散度是矢量场的一种强度性质，就如同密度、浓度、温度一样，它对应的广延性质是一个封闭区域表面的通量，所以说散度是通量的体密度。物理上，散度的意义是场的有源性。某一点或某个区域的散度大于零，表示向量场在这一点或这一区域有新的通量产生，小于零则表示向量场在这一点或区域有通量湮灭。

在三维直角坐标系 xyz 中，设向量场表示为：

场的分量P,Q,R具有一阶连续偏导数，那么向量场的散度就是：

既然向量场某一处的散度是向量场在该处附近通量的体密度，那么对某一个体积内的散度进行积分，就应该得到这个体积内的总通量。事实上可以证明这个推论是正确的，称为高斯散度定理。高斯定理说明，如果在体积V内的向量场拥有散度，那么散度的体积分等于向量场在V的表面的曲面积分：

三、物理学基础

1 、电通量（electric flux）和高斯定理（Gauss’s Law）

之所以引入电通量这个概念主要是为了计算带有电荷物体的电场强度。

在电磁学中，电通量是电场的通量，与穿过一个曲面的电场线的数目成正比。曲面S上的电通量由以下的曲面积分（surface integral）公式给出：

其中E是电场强度，dA是闭曲面S上的面积矢量的微分，其法线指向外侧。运算符号“.”表示两个矢量的点乘（dot product），因此电通量是一个标量。

对于封闭的高斯曲面，电通量由以下公式给出：

其中Qs是闭合曲面所包含的净电荷（包括自由电荷和束缚电荷），ε0是真空电容率（permittivity of free space或者vacuum permittivity）。这个关系即为电场的高斯定律的积分形式。它也是麦克斯韦方程组的四个方程之一。

2、静电平衡（electrostatic Equilibrium）

静电平衡是指导体中的自由电荷（通常为带负电荷的电子）所受到的力达到平衡而不再做定向运动的状态。静电平衡时，带电导体上的电荷分布有以下几个特点：

（1）导体内部电场强度为0，整个导体都是一个等势体。我们假设带电导体的内部电场强度不是0的话，自由电子会在电场的作用下移动，而不会是平衡状态

（2）导体内部没有静电荷，正负净电荷只分布在导体的外表面。根据库伦定理，多余的电荷是互相排斥的，静电力会让那些多余的电荷分布的尽量的远

（3）带电导体的表面电场强度垂直于表面且其大小和表面电荷密度成正比。如果不是垂直与表面，那么一定有切线上的分量，从而导致自由电子的移动

（4）在导体表面，越尖锐的地方，电荷的密度（单位面积的电荷量）越大，凹陷的位置几乎没有电荷。称为尖端放电现象。

3、利用高斯定理来计算带电荷平板的电场强度

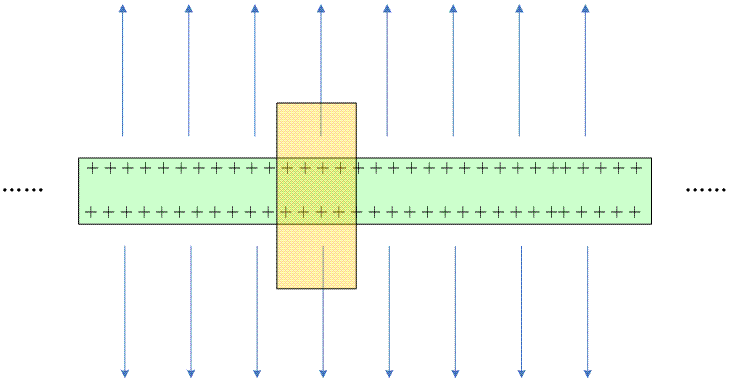
在掌握了高斯定律之后，我们可以利用这个定律和对称性原理来计算带电荷平板的电场强度。我们先计算一个无限长的带电平板导体周围的电场强度。根据上上节课的描述，电荷都是分布在导体的表面，我们假设电荷的密度是b库伦/平方米。示意图如下：

由于无限长的带电平板是对称的，因此平板的上面的电场和下面的电场大小是相等的，并且方向相反。此外，电场强度（矢量）应该是垂直于平板表面的。我们选择一个闭合的圆柱体的高斯曲面，如途中黄色的区域。由于侧面和电场方向是平行的，因此流过圆柱体侧面的电通量是0。需要注意的是在导体内部的那个圆柱体侧面，由于导体内部的电场强度等于0，因此，穿过平板导体的那部分圆柱体侧面的电通量也是0。流过圆柱体顶面的电通量是E x 2A。其中A是圆柱体顶面或者地面的面积。根据高斯定律：

因此，无限长的带电平板的电场是一个均匀场，场强的大小是：

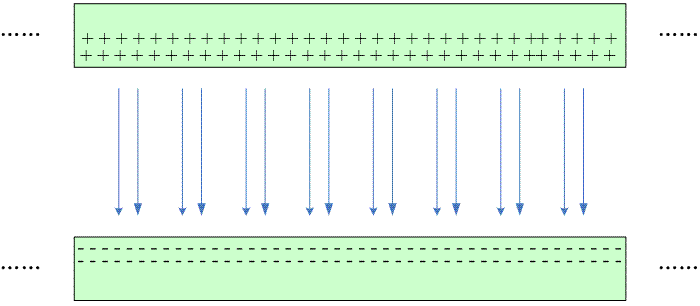
对于带负电的无限长的平板导体，其电场也是均匀场，只不过方向和上面的电场方向相反，当我们把这两块平板导体放在一起的时候，由于电场满足叠加定律，因此其电场的情况可以参考下图：

也就是说，两个平行的带电的平板导体（我们称之平板电容）之外的电场强度等于0，而内部的电场强度会double，也就是说平板电容内部的电场强度是：

四、电容（electrical capacitance）

1、电容的基本概念

电容是描述一个物体存储电荷能力的参数。任何物体都有其电容参数，例如地球、人体。电容被定义为：

从上面公式可以看出，电容就是单位电压下存储电荷的能力。电容的单位是法拉（Farad）。1法拉等于1库仑每伏特，即电容为1法拉的电容器，在正常操作范围内，每增加1伏特的电势差可以多储存1库仑的电荷。

2、平板电容

常见的电容器是平板电容器，它是由互相平行、以空间或介电质（dielectric）隔离的两片薄板导体构成。当给两片导板之间的加上V的电压的时候，两片导板分别携带了＋Q和－Q的电荷，导板之间形成均匀电场。根据上节的知识可知电场为：

A是平行板电容器的两片导板的面积。是电介质的电容率（permittivity）。对于真空，其电介质的电容率是ε0，也就是传输中的真空电容率。如果两个平板相距d，这时候，两个平板之间的电压差等于Ed（电压差应该是电场强度和距离矢量微分点积的曲线积分，不过由于是均匀电场，因此曲线积分变成相乘）。

根据电容公式，平板电容可根据如下公式进行计算：

根据电容公式，要想增加电容值，可以加大平板电容的面积（这也是为何在电容使用卷曲的方式塞进一个圆柱体中，主要为了增加A），减少两个金属平板之间的距离或者使用电容率比较大的材料放置到平板电容之间。

电容是一个储能器件，当电容放电就是能量释放的过程。下面我们从能量的角度来看看平板电容器。我们假设刚开始的时候，电容器的两个平板都是不带电的，因此电势相等，没有电压（电势差）。当把一个微小的dQ电荷从负极板移动到正极板，这时候，正极板携带dQ的正电，负极板携带dQ的负电，两块电极板之间会有均匀电场，就会产生电压dV＝（1/C）dQ。一旦有了电压差，随后电荷的移动就需要克服电场力做功，公式如下：

dW＝E x dQ x d＝V x dQ＝（1/C）QdQ

其中V就是进行dQ搬移时候的电压差，这个值是不断变化的，是Q的函数。当完成Q库伦的电荷搬移之后所做的total work应该是对上面的公式进行积分运算，最终可以得到结果是：

W＝（1/2）QV ＝ （1/2）CV^2

一个电容能存储多少能量是和其电容参数相关，C越大，储能越多。如果固定了C，电压越大，储能越大，不过电压不能无限制的增加，当大到一定程度的时候，电容器会被击穿。

3、如何计算地球的电容？

当使用电容这个术语的时候通常是讲的“互电容”（mutual capacitance），比如：平行板电容器的两片平板导体之间的电容。当计算单独导体的电容的时候，需要使用另外一个术语叫做“自电容”（self-capacitance），即单独导体的电势每增加1V所需的电荷量。对于自电容，我们需要设定一个电势为0的参考面。我们一般假设这电势等于零的参考点为一个理论球壳导体，其半径为无穷远，其球心与单独导体同心。

地球是一个导体，我们可以把地球看成是半径为R的球形导体，利用高斯定律（选取和地球同心的球面作为高斯曲面）可以计算出携带Q库伦电荷的地球周围的电场强度：

对E进行曲线积分（积分曲线选择从无穷远处到半径等于R的球面上的任意一点上的曲线）则其球表面电势为：

其自电容是：