基本电路概念(一)什么是电压？

基本电路概念之（一）：什么是电压？

作者：linuxer 发布于：2014-5-16 10:40 分类：基础学科

一、前言

我有一个奇葩儿子（4岁），经常问一些奇葩的问题。比如：为什么电子带负电？什么是电压？电路板是怎么生产的？发动机的内部结构是什么？……总之，各种问题层出不穷。有一天回家，他正和他妈妈一起看几张医学的CT片子（他妈妈是医生），他妈妈正详细向他解释该病人颅部血管病变问题，各种专业术语丝毫也没有浇灭儿子的热情，那认真的劲头，我当时就震惊了。

为了应付我这个奇葩儿子，为了始终维持爸爸的高大形象，我不得不对这个世界有更深层次的思考……这次的主题是：什么是电压？电池为什么能提供电压？

一、如何向小朋友解释电压和电池的概念？

儿子有一套电子积木，无论是让小灯泡亮，让电机转动，让喇叭出声音都需要电池这样一个元件。其他的元件都是有很直观的声音、光或者旋转的表现，只有电池，他不是非常的理解，也是问我：爸爸，电池是什么东西？有什么作用？我回答：电池就是产生电压，压着小电子在电线中跑，小电子在电线中跑，所以可以点亮小灯泡哦。儿子追问：什么是电压？为了让小朋友理解电压，我们一起做起了实验。

实验器材包括：
1、    漏斗一个
2、    一个2米长的导管（导管的截面积要小）
3、    水桶一个
4、    大勺子一个
首先将漏斗底部接上2米长的导管，导管的另外一头插入水桶，水桶事先先接半桶水。将漏斗悬挂到1.8米的高度，用勺子不断的将水从水桶舀到漏斗中，水于是在导管中形成水流，又回到水桶中。我和儿子玩的不亦乐乎，在一起玩的过程中，我顺便向儿子解释：水就类似小电子，一个是在水管中流动，一个是在电线中流动。为了让水持续流动，我们必须不断的用勺子舀水，把水输送到位置比较高的漏斗中。而电池里面也有很多的小勺子，小电子从负极流动到正极，在电池的正极，小勺子会把小电子舀回负极，这样就可以产生电压，让小电子不断的流动了。

二、和工程师讨论电压和电池的相关概念

“电压就是电势差”这是工程师耳熟能详的话，但什么是电势？

我们首先从能量角度来看。正所谓水往低处流，其实就是说“水”倾向于从势能高的地方流向势能低的地方。其位置高，具有更多的势能。当流向势能低的位置的时候，虽然损失了势能，但是获得了动能。这些概念在初中就建立起来的概念，只不过，更准确的说，这里的势能应该是“重力场势能”。

和“重力场势能”概念类似，电势就是“电场势能”。重力场就算你不理解，也能对这个术语有感觉，毕竟每个人都处在地球的重力场中。处于重力场中，只要你有质量，就会收到一个沿着重力场方向的力。那么什么是电场（electric field）？毫无疑问，电场也是和力有关系的，这里就是电场力（库伦力）。我们都知道库仑定律：在真空中两个静止点电荷之间的相互作用力与距离平方成反比，与电量乘积成正比，作用力的方向在它们的连线上，同号电荷相斥，异号电荷相吸。这种静电荷之间的作用力就叫做库伦力。

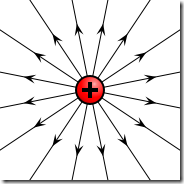
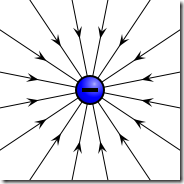
相信工程师对库仑定律还是有印象的，在此基础上，我们可以展开对电场这个概念的描述。其实电场只是为了描述静电力（库伦力）而引入的一个工具。首先，电场是矢量场（vector field），有方向和大小。将1库伦的电荷放入到电场中的一个点上，那么该点受到的库伦力的大小就是该点的电场强度。我们可以使用电场线（electric field line）来描述电场。例如点电荷的电场如下图（该图片来自WiKi）所示：

上面的图片很好的展示了电场的方向，但是电场的大小没有展示出来。点电荷产生的电场，与距离的平方成反比。当一个携带正电荷的物质处于电场中的时候，该物质会收到一个沿着电场方向的力。了解了电场概念后，再回到静电势能（electrostatic potential energy）这个概念。我们用带正电的点电荷的电场来解释静电势能，如下图所示：

灰色的正电荷产生了一个电场，充满了整个三维空间。绿色的测试电荷位于无穷远处，并且处于静止状态。现在，我们使用外力推动测试的绿色正电荷逆着电场方向运动，逐渐靠近灰色的电荷。这时候，我们的外力克服了静电力，将该正电荷移动了一段距离，从物理上讲，外力做了功，但是该正电荷开始是静止的，移动了一段距离后仍然是静止的，动能没有变化，那么我做的功上哪里去了？其实功被转化成了势能。 由于电场位置而具备的能量叫做静电势能。

电势（electric potential）定义为处于电场中某个位置的单位电荷所具有的静电势能。如上图，沿着电场方向有两点A和B。如果我们从B点将1库伦的电荷运送到A点，克服电场力做的功是1焦耳，那么A点的电势和B点的电势差就是1V。

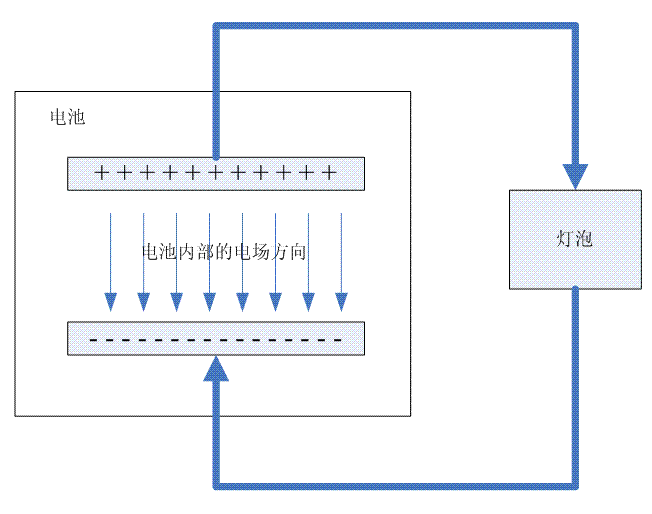
OK，我们已经了解了电势差的概念了，现在可以看看电池的内部结构了。我们抽象一个电池和灯泡组成的电路如下：

我们假设电池是由带正电和负电的两块电板组成，当导体连接了电池的正极和负极的时候，由于电势差的作用，电子从负极流向正极（导体中实际流动的是电子，但是由于富兰克林在定义正电和负电的时候是任意定义的，因此有50％的机会让电子的运动方向和电流方向一致，很遗憾，他的定义是反的）。因此，在正极板上会有电中和现象发生，从而导致电势差降低。为了维持电势，在电池内部，必须把电子从正极移动到负极。但是这样的移动是要克服电池内部的电场力做功，必须有其他的能量连强迫这样的电子移动。对于电池，这就是化学能。因此，电池内部，化学能让电子克服电场力从正极移动到负极，在电池外部，电势差导致电子从负极移动到正极，形成电流。

三、基础数学知识

本章节描述了理解电压的相关数学知识，只有了解了本节的数学知识才能理解第四节的内容。

1、方向导数（directional derivative）和梯度（gradient）

我们用三元函数来说明方向导数和梯度，对于n元函数，其概念是类似的。

对于三元函数f（x，y，z），我们定义点（x₀，y₀，z₀）上的偏导数：

该偏导数表示函数值在点（x₀，y₀，z₀）上沿着x轴的变化快慢情况。同理可以定义函数值在点（x₀，y₀，z₀）上沿着y轴和z轴的变化率（也就是对自变量y和z的偏导数）。在处理具体问题的时候，例如在研究气压在某个特定方向上的变化率情况的时候，仅仅定义自变量的偏导数就不能满足要求了。

我们定义一个过（x₀，y₀，z₀）的直线 l 的参数方程如下：

我们定义函数在（x₀，y₀，z₀）点沿直线l的方向导数为：

从上面的定义就可以看出，某点的方向导数实际上就是定义了函数f在该点上沿直线 l 的变化率。

如果f（x，y，z）在（x₀，y₀，z₀）点可微（differentiable），那么：

由于自变量的变化是沿着直线l的方向，因此：

由此可知函数的方向导数可以用函数的各个偏导数计算：

是直线 l 的方向余弦。我们可以定义 l 方向上的单位向量：

如果f（x，y，z）可微（differentiable），f（x，y，z）的梯度矢量被定义如下：

由上面的定义可得：

是梯度矢量和直线l上单位矢量的夹角。由此可知，梯度矢量的方向就是方向导数取得最大值的方向。而梯度的模就是该方向的方向导数。

三元函数f（x，y，z）在xyz坐标系中，每一个点（x，y，z）都对应一个函数值f（x，y，z），这些函数值是一个标量。这个函数也被称为标量场（scalar field）。函数f的在某点的梯度是一个矢量，其分量就是f在该点的各个坐标轴方向的偏导数（partial derivative）。这样，求一个函数的梯度也就把一个标量场变成梯度矢量场（gradient vector field）。梯度就类似于一元函数的导数（derivative）。

 

2、曲线积分（Line Integral）

在数学中，曲线积分是积分的一种。和普通定积分不一样的是：其积分区间不是自变量的集合，而是特定的曲线，称为积分路径。对于曲线积分而言，被积函数可以是标量函数（标量场）或矢量函数（矢量场）。对于标量场，积分的值是路径各点上的函数值乘上相应的权重（一般是弧长）的黎曼和；对于矢量场，积分的值是路径各点上的函数值（该函数值是矢量）与曲线微元矢量的标量积（例如点积）的黎曼和。

我们这里主要关注矢量场的应用场景：考虑变力沿曲线做的功。这时候，曲线上每一个点上的力F是一个矢量。而位移也是一个矢量，这时候可以通过曲线积分来计算变力沿曲线做的功：

是位移向量（displacement vector）的微分，是力做功的微分。

 

3、保守矢量场

我们用三维空间来描述场、标量场和矢量场的概念，对于n维空间是一样的。

对于一个三维空间中的任意点（x0，y0，z0）都有一个确定的数量f（ x0，y0，z0）与之对应，那么我们称函数f（ x，y，z）确定了三维空间上的一个标量场（例如温度场）。对于一个三维空间中的任意点（x0，y0，z0）都有一个确定的矢量F（ x0，y0，z0）与之对应，那么我们称矢量值函数F（ x，y，z）确定了三维空间上的一个矢量场（例如力场，电场）。矢量值函数F（ x，y，z）可以进行分解，从而用数量函数表示：

F（ x，y，z）＝P（ x，y，z）i ＋ Q（ x，y，z）j ＋ R（ x，y，z）k

其中，P、Q、R是数量函数，是矢量函数在x、y、z轴上的投影。

通过求梯度，可以把一个标量场f（ x，y，z）变成矢量场，我们记作grad f（ x，y，z），这个矢量场就称为梯度场。而原来的那个标量场函数f（ x，y，z）就叫做这个梯度场的标势（scalar potential ）。在矢量分析中，保守矢量场定义为某些函数的梯度。

在进行曲线积分的时候，我们可以使用微积分基本定理来简化曲线积分的运算：

曲线是从p0到p1。上面的定理可以表述为对梯度场（保守矢量场）的线积分可以用其原函数（scalar potential ）来计算。公式是冰冷的，如果带入物理学的概念就比较生动了。左边是保守力沿曲线C做的功，右边是终点的势能减去初始点的势能，这两个数值是相等的。也就意味着保守力沿曲线做的功是和路径无关，只是和起点和终点的位置有关。根据上面的公式，还可以推出：如果曲线C是闭合的（p0等于p1），那么其积分等于0。也就是说，对于保守力场，在闭合曲线上做的功等于0。

既然保守矢量场有这些好的特性，那么如何判断一个vector field是保守的呢？对于，二维空间，如果一个vector field＝Mi＋Nj在平面上的每一个点都是可微的，并且Nx＝My，那么该向量场就是保守场。

 

四、数学的引入

有了section 3的基础，我们可以对section 2中描述的很多概念进行更精确的定义。

1、库仑定律

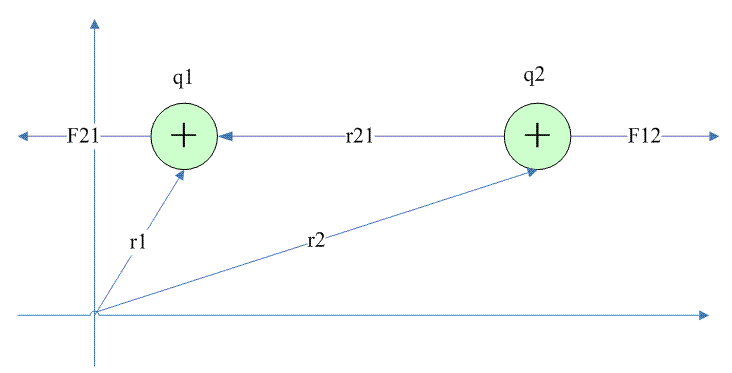
矢量形式的库仑定律定义如下：

是从q2指向q1的单位矢量（unit vector）。

是从q2指向q1的矢量。矢量长度等于q1到q2的距离。和分别表示q1和q2的距离矢量。

是q2施加给q1的力（是一个vector）

静止点电荷之间的相互作用力遵循库仑定律。又称库仑力（Coulomeb force）或者静电力（electrostatic force）。库仑力满足叠加定理。

静电力作功与路径无关，是保守力（Conservative force），因此我们可以定义势能函数（保守力场的原函数，对该函数求梯度可以得到保守力场）。其势能函数（标量场）定义为：

q1在原点，q2位于空间任意位置，其坐标为（x，y，z），

因此，势能函数U的梯度是：

定义是径向的单位矢量，那么势能函数U的梯度就是库伦力场（数学上的势能定义和物理学上的势能定义相差一个负号）。因此可以判断静电力场这个矢量场是一个梯度场，也就是说静电力是保守力。

 

2、电场的概念

电场只是为了描述静电力而引入的一个工具。和静电力一样，电场也是矢量。电场是矢量场（vector field），我们定义电场内某一点的电场强度（矢量）等于静电力除以放置于该点的电荷电量。

是放置于该点的测试电荷（test charge）的电量。根据电场的定义，电场强度E的单位是N/C，也就是每库伦的电荷在电场中的静电力。我们可以把电场强度和加速度做一个类比：

电场强度 ＝ 静电力/电荷电量

加速度 ＝ 万有引力/质量

对于重力场和静电场，电场强度对于电荷可以类比加速度对于质量。

对于点电荷（point charge），其电场定义如下：

是从点电荷的位置指向测试电荷的unit vector。

 

3、 电势能（electric potential energy）和电势（electric potential）

在静电学里，电势能被称作静电势能（electrostatic potential energy）。它是一种由于库伦力而定义的势能（类似针对万有引力定义的引力势能）。它是由在电场中的位置决定的势能。

在计算静电势能的时候，我们需要引入一个参考点。我们定义将电荷从参考位置移动到指定的位置所做的功（work）的负数就是该点的静电势能。在数学上，力沿曲线做的功用曲线积分（line integral）来计算：

是静电力。空间中，一个点电荷的电场是一个矢量场，同样的，位于该电场的电荷所受到的静电力也是一个矢量力场。运算符号“.”表示向量的点积（dot product）。是位移向量（displacement vector）的微分。一般而言，可以定义无穷远为参考点。

在静电学里，电势（electric potential）定义为处于电场中某个位置的单位电荷所具有的电势能。

电势的单位为V（伏），1V=1J/C（1焦/库）。静电场中电势相等的点构成一些曲面，这些曲面称为等势面。电场线总是与等势面正交，并指向电势降低的方向，因此静电场中等势面的分布就绘出了电场分布。电势场是一个标量场（scale vector field）。

我们可以以点电荷＋Q为例来计算电势，假设无穷远的电势等于0。

根据上面的公式，对于正电荷，其电势都是正的，越接近电荷的位置，电势越大，离开电荷越远，电势越小，无穷远处等于0。对于负电荷，其电势都是负的，越接近电荷的位置，电势越小（绝对值大），离开电荷越远，电势越大，无穷远处等于0。

在实际电路中，我们常常使用电压（voltage）这个术语，所谓电压其实就是电势差（electrical potential difference），定义空间中A，B两点的电压如下：