卷积
作者:镜面狐
链接:https://www.zhihu.com/question/22298352/answer/96263002
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
链接:https://www.zhihu.com/question/22298352/answer/96263002
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
最近在看Feedback Control of Dynamic Systems,趁此机会复习了一下卷积。
先看下图,左边是输入信号,右边是输出信号:
![]()
(a)中,输入信号p(t)经过系统后得到输出信号h(t);
(b)中,输入信号较之于(a)延迟了τ,表示为p(t-τ),由于是LTI(线性时不变系统),输出信号也延迟τ,变为h(t-τ);
(c)、(d)两图阐释了LTI的叠加原理:若以p(t)+p(t-τ)为输入,则输出为h(t)+h(t-τ);
假设现在有一个输入信号u(t),将其表示为若干个我们刚刚见过的p(t)的叠加
![]()
![]()
那么u(t)通过上文的系统后,会得到什么呢?
假设可得y(t),根据叠加原理:
![]()
![]()
![]()
但我们仍有一些不太满意的地方,用p(t)表示的u(t)并不是精确的u(t)啊,那些小长条的面积比u(t)的面积可少了不少呢。除非Δ尽可能的小,长条尽可能的窄。
诶,这不就是积分么?
所以:
![]()
这就是卷积,与其理解成翻转,不如理解成延迟后叠加。
先看下图,左边是输入信号,右边是输出信号:
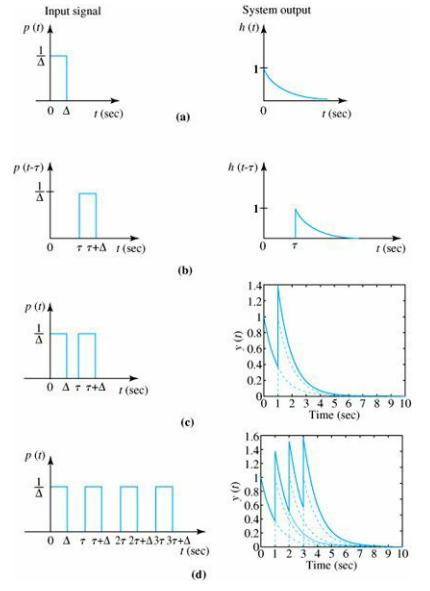
(a)中,输入信号p(t)经过系统后得到输出信号h(t);
(b)中,输入信号较之于(a)延迟了τ,表示为p(t-τ),由于是LTI(线性时不变系统),输出信号也延迟τ,变为h(t-τ);
(c)、(d)两图阐释了LTI的叠加原理:若以p(t)+p(t-τ)为输入,则输出为h(t)+h(t-τ);
假设现在有一个输入信号u(t),将其表示为若干个我们刚刚见过的p(t)的叠加
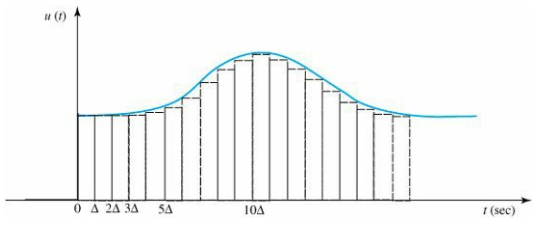
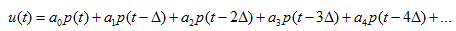
那么u(t)通过上文的系统后,会得到什么呢?
假设可得y(t),根据叠加原理:
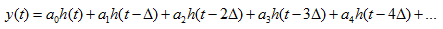
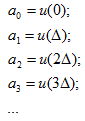
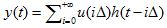
但我们仍有一些不太满意的地方,用p(t)表示的u(t)并不是精确的u(t)啊,那些小长条的面积比u(t)的面积可少了不少呢。除非Δ尽可能的小,长条尽可能的窄。
诶,这不就是积分么?
所以:
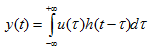
这就是卷积,与其理解成翻转,不如理解成延迟后叠加。
-----------------------------------------------------------------------------------------------------
作者:林扬飞
链接:https://www.zhihu.com/question/22298352/answer/27993829
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
链接:https://www.zhihu.com/question/22298352/answer/27993829
来源:知乎
著作权归作者所有,转载请联系作者获得授权。
卷积在信号与系统这门课程里面使用得比较多,可以说卷积就是信号与系统这门课程的一道坎,把卷积的概念弄清楚了,信号与系统其他一些概念都很明了了。因此,结合信号系统来更为形象地理解什么是卷积。
![]()
![\delta (t)]() 单位冲激信号:
单位冲激信号:
![]()
测得系统的响应为:
![]()
类似于敲锣的例子,敲打锣面就是上面第一幅图所示的冲激信号,锣面发生振动的幅度就如同上面第二幅图所示。通过这种方法反映了系统的特性,如果用一个输入-输出对应的函数来表示系统,上面这个图形对应的函数就称为系统函数。当然,实际的系统输入并不是一个的单位冲激信号这么简单,但无论多么复杂的输入信号,我们都可以将其分解为一个个连续的冲激信号,下面3幅图就分别显示了t=0s,t=0.2s,t=0.4s时给系统输入单位冲激信号,系统的响应:
![]()
![]() 由于3个单位冲激信号有0.2s的延时,因此系统的3个响应图形也响应有0.2s的延时,最后我们将蓝、红、绿3个响应图形相加起来就得到了3个单位冲激信号通过系统的输出:
由于3个单位冲激信号有0.2s的延时,因此系统的3个响应图形也响应有0.2s的延时,最后我们将蓝、红、绿3个响应图形相加起来就得到了3个单位冲激信号通过系统的输出:![]() 由于3个单位冲激信号有0.2s的延时,因此系统的3个响应图形也响应有0.2s的延时,最后我们将蓝、红、绿3个响应图形相加起来就得到了3个单位冲激信号通过系统的输出:
由于3个单位冲激信号有0.2s的延时,因此系统的3个响应图形也响应有0.2s的延时,最后我们将蓝、红、绿3个响应图形相加起来就得到了3个单位冲激信号通过系统的输出:
![]()
- 系统
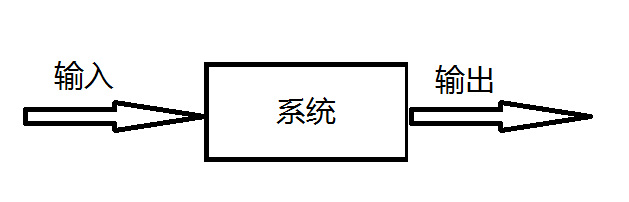
- 响应

测得系统的响应为:
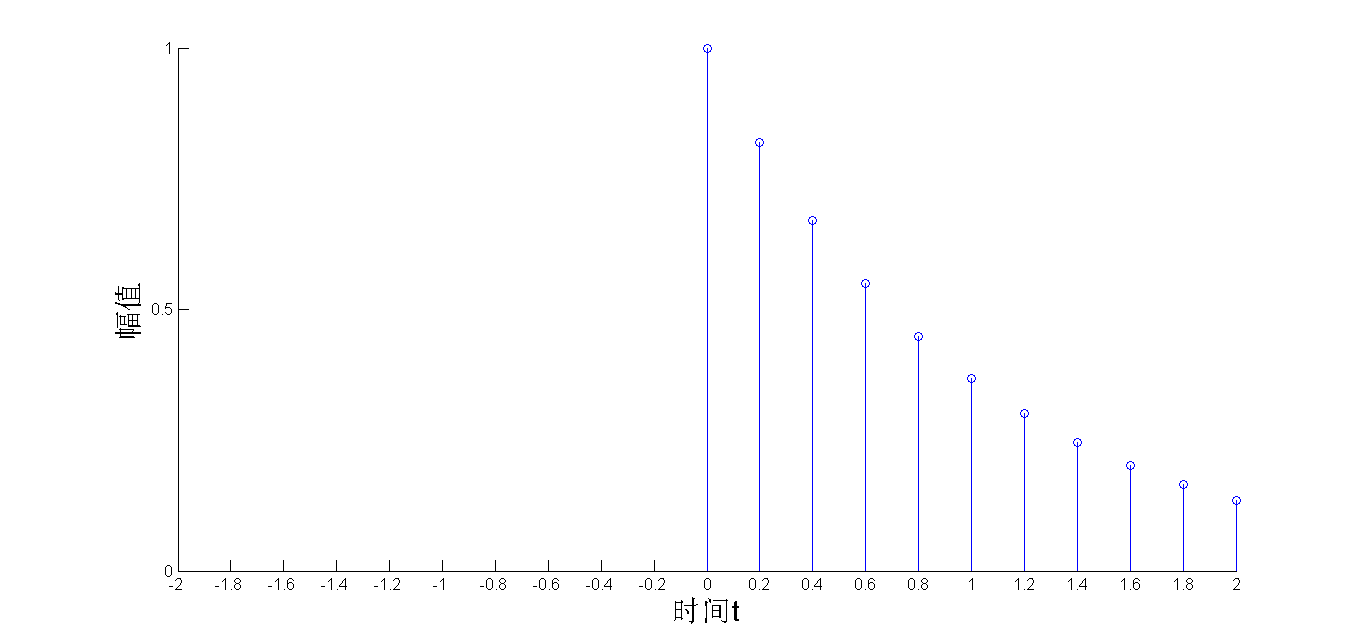
类似于敲锣的例子,敲打锣面就是上面第一幅图所示的冲激信号,锣面发生振动的幅度就如同上面第二幅图所示。通过这种方法反映了系统的特性,如果用一个输入-输出对应的函数来表示系统,上面这个图形对应的函数就称为系统函数。当然,实际的系统输入并不是一个的单位冲激信号这么简单,但无论多么复杂的输入信号,我们都可以将其分解为一个个连续的冲激信号,下面3幅图就分别显示了t=0s,t=0.2s,t=0.4s时给系统输入单位冲激信号,系统的响应:
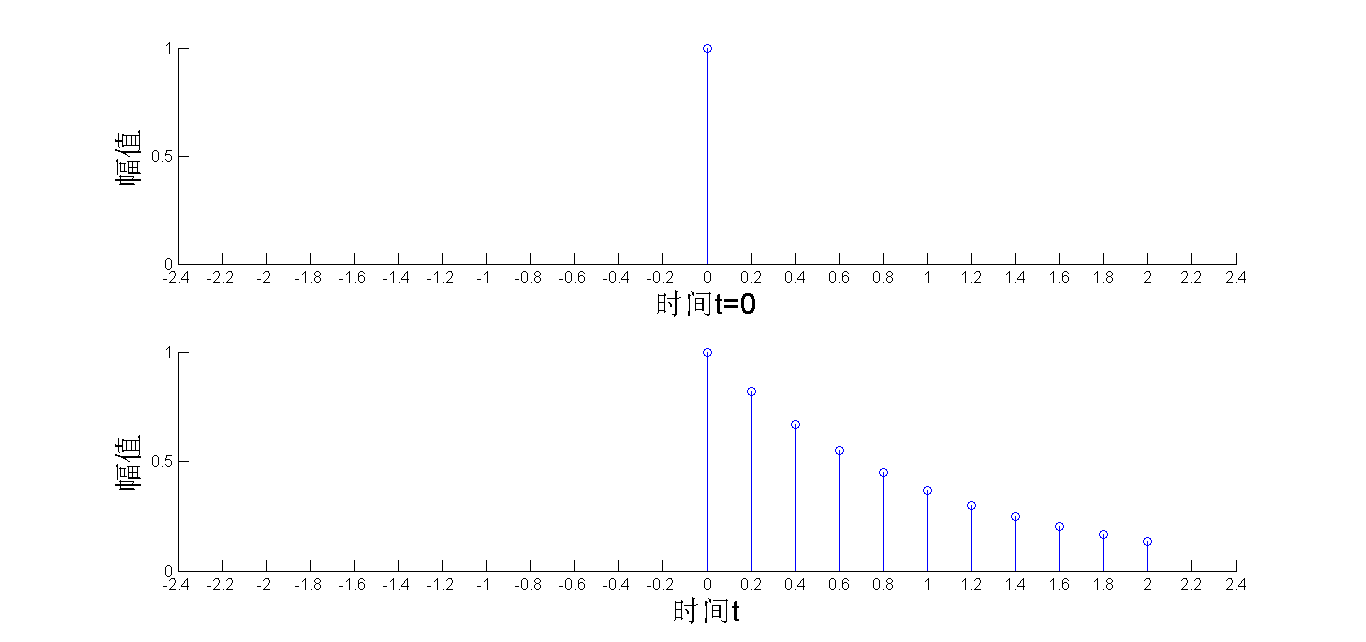
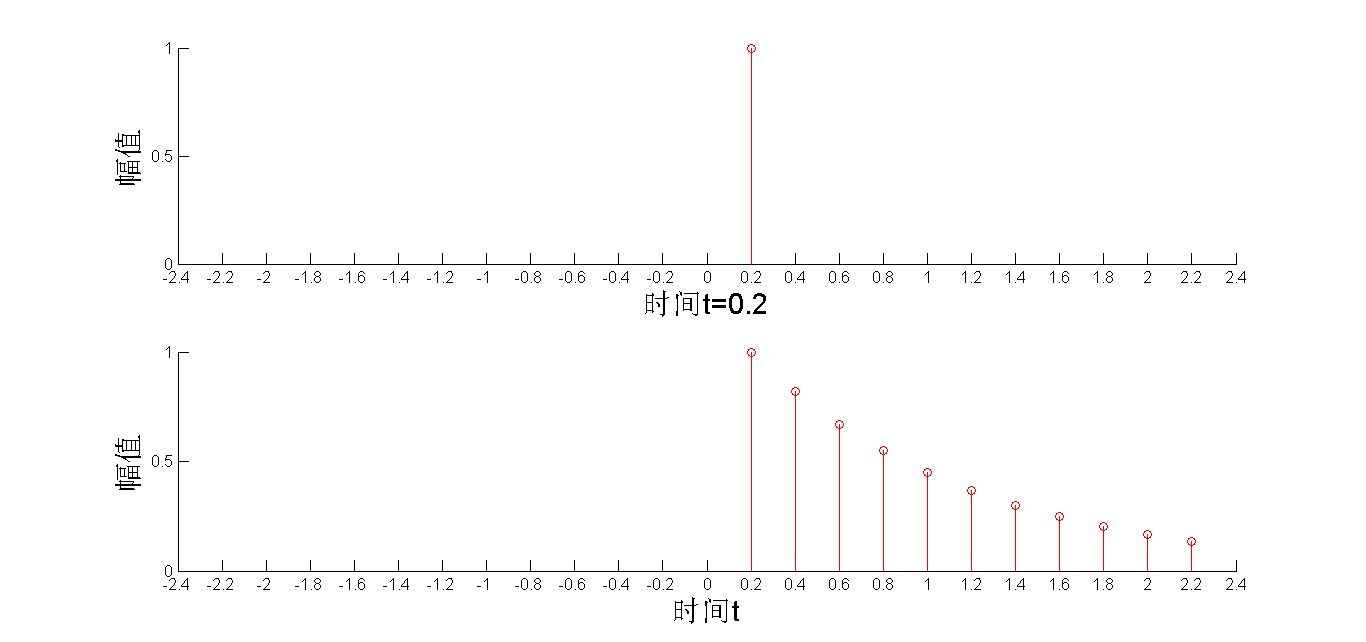 由于3个单位冲激信号有0.2s的延时,因此系统的3个响应图形也响应有0.2s的延时,最后我们将蓝、红、绿3个响应图形相加起来就得到了3个单位冲激信号通过系统的输出:
由于3个单位冲激信号有0.2s的延时,因此系统的3个响应图形也响应有0.2s的延时,最后我们将蓝、红、绿3个响应图形相加起来就得到了3个单位冲激信号通过系统的输出: 由于3个单位冲激信号有0.2s的延时,因此系统的3个响应图形也响应有0.2s的延时,最后我们将蓝、红、绿3个响应图形相加起来就得到了3个单位冲激信号通过系统的输出:
由于3个单位冲激信号有0.2s的延时,因此系统的3个响应图形也响应有0.2s的延时,最后我们将蓝、红、绿3个响应图形相加起来就得到了3个单位冲激信号通过系统的输出: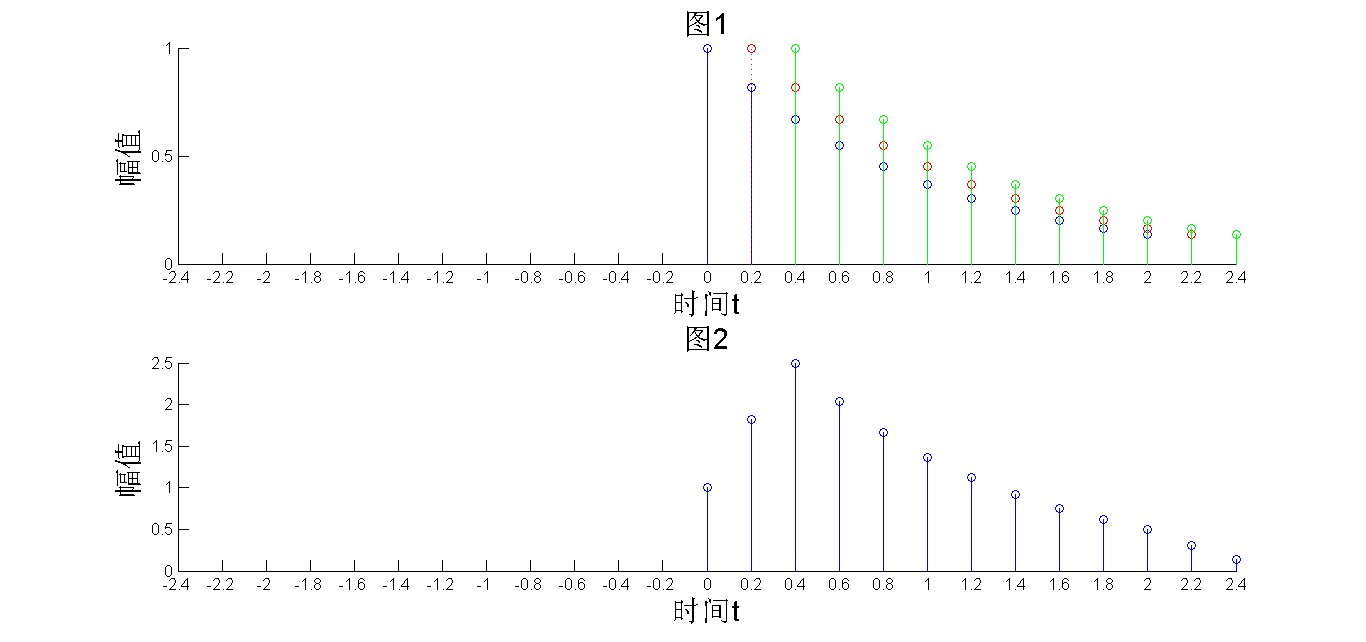
- 卷积



 浙公网安备 33010602011771号
浙公网安备 33010602011771号