清北学堂2020.11笔记
11.23
模拟赛(上午)
T1 \(20\) AC
发现 \(n\) 比较大的时候答案就恒为 \(0\) 了。
把模数写成 \(2^{31}\) 了,,,
技巧:可以用 Dev-C++ MinGW64\bin 目录下的 size.exe 测空间使用。
T2 \(100\) AC
枚举每个位置,然后算一下能放的数的范围即可。
T3 \(40\) AC
首先,发现对于长度为 \(n\) 的 \(n!\) 种序列,其逆序对个数只有 \(O(n^2)\) 种取值。于是可以用 \(f_{S,j}\) 表示用的数为二进制状态 \(S\),逆序对为 \(j\) 个的方案数。这部分的时间复杂度为 \(O(2^nn^3)\) 且常数极小(大概是 \(\frac{1}{4}\))。
一个序列如果只用 \(1,2\) 两种操作,其花费只与逆序对个数有关。所以可以统计 \(O(n^2)\) 种序列的最小花费,排一下序。
如果对于一个序列进行 \(3\) 操作,那么其实花费就和原序列没有什么关系了。用 \(f_s\) 表示序列 \(s\) 的最小花费,则这个花费固定为 \(c+\bar{f}\),\(\bar{f}\) 即为所有 \(f_s\) 的平均值。
然后考虑怎么计算 \(\bar{f}\)。可以发现其实对于每个 \(f_s\),都能表示为 \(f_s=\begin{cases} C_s&C_s\le x\\ c+\bar{f}&C_s>x \end{cases}\),其中 \(x\) 为一个阈值,\(C_s\) 为序列 \(s\) 只用 \(1,2\) 操作的最小花费。
枚举这个阈值,即可得出答案。时间复杂度 \(O(2^nn^3+(\sum d)n^2\log n))\)。
注意中间计算分数的时候可能会爆 long long,因此要用 double 来比较分数的大小。
T4 \(50\) AC
如果点 \(x\) 在路径 \((i,j)\) 上,则一定有 \(dis(i,x)+dis(j,x)=dis(i,j)\),反之亦然。
推广到 \(k\) 棵树上,\(\sum dis_k (i,x)+dis_k (j,x)=\sum dis_k (i,j)\)。
预处理出 \(dis\),枚举 \(i,j,x\) 判断即可。
模拟赛(晚上)
T1 \(100\) AC
\(a \operatorname{xor} b\le a+b\),\(a \operatorname{and} b\le a \operatorname{or} b\le a+b\)。
T2 \(100\) AC
推一下状态转移方程,发现状态的转移和自身有关,化简一下式子,就可以得出 \(O(1)\) 计算的方法。
T3 \(90\) AC
十分神妙的线段树。用懒标记 \(a,b,c\) 表示真实的数 \(=\lfloor\frac{a}{b}\rfloor+c\)。如果除的数过大,就把 \(b\) 设为 \(\inf\),\(a\) 设为 \(0\)。
T4 \(30\) WA
枚举 \(x=\frac{i}{2}\),通过这样可以确定这个最大值 \(i\) 的一半在某个元素或者某两个元素之间的位置。考虑让右边的所有元素和左边的所有元素匹配,可以发现对于每个元素,它能匹配的元素数量都是一个定值(右边那个元素减少一,则左边可以匹配的元素个数增加一,但因为以前用过了一个元素,所以还是原来的数)。于是快速幂一下即可,但我不知道哪里写挂了。
11.24
模拟赛
T1 \(90\) AC
枚举选择的商品的总价格在第 \(i\) 位上 \(\le k\),即从低到高 \(1\dots (i-1)\) 位任意,第 \(i\) 位上 \(k\) 必须是 \(1\) 且总价格的第 \(i\) 位必须是零,第 \((i+1)\dots 31\) 位必须是 \(k\) 的子集(即 \(a_{j,(i+1)\dots 31} \operatorname{or} k_{(i+1)\dots31}=k_{(i+1)\dots31}\))。然后算一下即可,时间复杂度 \(O(30n)\)。
T2 \(100\) AC
T3 \(30\) AC
好劲爆的 T3。
设 \(f_{i,l,r,j},g_{i,l,r,j}\) 分别表示后 \(i\) 列,第 \(l\sim r\) 行,最小值 \(\ge j\) 的方案数以及总和。
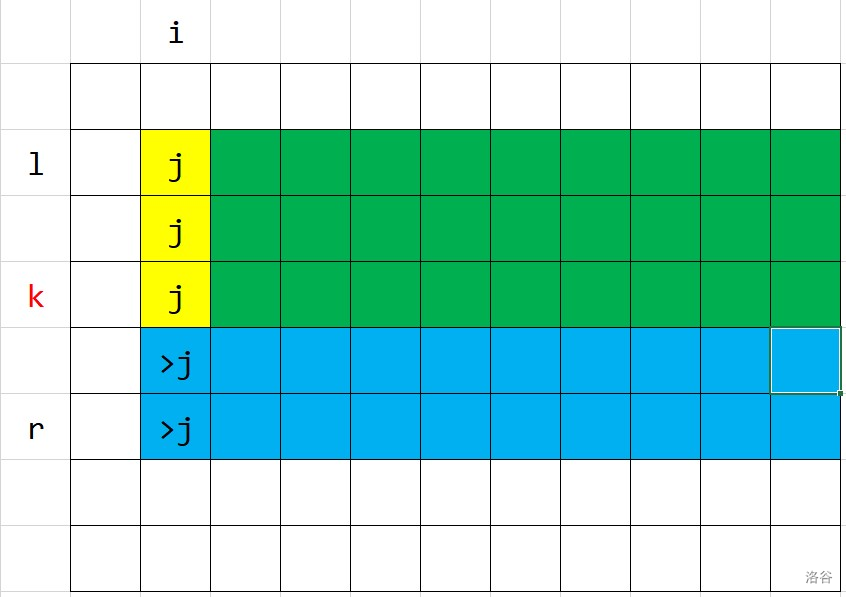
如图,枚举 \(k=l \sim r\),\(l\sim k\) 即为填 \(j\) 的区域。此时 \(f_{i,l,r,j}=f_{i,l,r,j+1}+\sum \limits_k f_{i+1,l,k,0}\text{(绿色区域)}\times f_{i,k+1,r,j+1}\text{(蓝色区域)}\)。
同理,\(g=(f_黄\times g_绿 + g_黄 \times f_绿)\times f_蓝 + g_蓝\times f_绿\)。这里就体现出来 \(f\) 的奇妙用处了。
代码片段:
p10[0]=1;
For(i,1,m) p10[i]=p10[i-1]*10%MOD;
For(i,1,n) f[m+1][i][i][0]=1;
Dec(i,m,1){
For(len,1,n){
for(int l=1,r=l+len-1;r<=n;++l,++r){
Dec(j,9,0){
ll &F=f[i][l][r][j],&G=g[i][l][r][j];
F=f[i][l][r][j+1],G=g[i][l][r][j+1];
For(k,l,r){
if(s[k][i]!=j+'0'&&s[k][i]!='?') break;
F=(F+f[i+1][l][k][0]*(k<r?f[i][k+1][r][j+1]:1))%MOD;
ll F1=f[i+1][l][k][0],G1=(g[i+1][l][k][0]+p10[m-i]*j*(k-l+1)%MOD*f[i+1][l][k][0]%MOD)%MOD;
G=(G+F1*(k<r?g[i][k+1][r][j+1]:0)%MOD+G1*(k<r?f[i][k+1][r][j+1]:1)%MOD)%MOD;
}
}
}
}
}
printf("%lld\n",g[1][1][n][0]);
T4 \(0\) 没做
不想管这题。
杂题
https://www.luogu.com.cn/problem/P4766 AC
区间 dp,设 \(f_{i,j}\) 为消灭左、右端点均在 \([i,j]\) 范围内的外星人的最小花费。可以发现每次消灭掉区间内 \(d\) 最大的就是最优方案。枚举在哪个时间点消灭,进行转移即可。
状态转移方程:\(f_{i,j}=\min\limits_{L\le k \le R}(f_{i,k-1}+d_{max}+f_{k+1,j})\),其中 \(L,R\) 为 \(d\) 最大的外星人的 \(a,b\)。
因为 \(a,b\) 的范围比较大,需要进行离散化。
11.25
模拟赛(上午)
T1 \(100\) AC
直接模拟即可。
T2 \(100\) AC
统计字母在每个字符串中出现的次数 \(cnt_{n,26}\)。枚举 Alice 选择的字符串 \(i\),可以发现前面必须填字母的出现次数 \(\ge\) 其他任意字符串中这个字母的出现次数。又可以发现当你填这些字符串时,顺序没有影响——当 \(c_1,c_2\) 顺序交换时,它们仍然会排除掉其余字符串中 \(cnt_{j,c_1}\le cnt_{i,c1}\) 或 \(cnt_{j,c_2}\le cnt_{i,c2}\) 的。于是枚举一下即可,注意常数。
T3 \(40\) AC
计算区间逆序对:
左端点 \(l\) 单调递增时,要使得区间逆序对保持为 \(k\),则 \(r\) 一定要单调递增。
于是 \(l,r\) 移动次数都是 \(O(n)\) 级别的,双指针扫一下即可。
算答案:
数论题的某种套路(?):增加枚举量、交换顺序。
其实是算贡献的思路。
现在,答案就变成了对于每个位置 \(i=1\dots n\),都有 \(C_{a_i}^2\),其中 \(a_i\) 为覆盖点 \(i\) 的区间个数。
回到“计算区间逆序对”的问题,一个逆序对为 \(m\) 的区间会产生 \(n-r_i+1\) 个新区间。可以发现 \(a_{r_i}\) 会增加 \(n-r_i+1\),\(a_{r_i+1}\) 会增加 \(n-r_i\)……
所以其实是对一个区间加等差序列。考虑在差分数组上乱搞即可,可以看 P1438。
T3 的另一个问题:
求这些区间有多少个是相交的。
算相交个数情况比较多,考虑算不相交的个数(补集转化)。
预处理出 \(cntl_n,cntr_n\),表示以 \(i\) 为左端点的区间个数、以 \(i\) 为右端点的区间个数。然后搞一下即可。
T4 \(0\) AC
先考虑 \(p_1=p_2\) 的情况,数据范围是 \(10^6\),因此考虑树形 dp。
设 \(f_i\) 为把以 \(i\) 为根的子树炸掉的方案数。可以发现在这棵子树中,\(i\) 一定是最后被炸掉的。所以
如果 \(p_1\neq p_2\):
考虑对 \(p_1,p_2\) 之间的链(及链上的点的子树)进行区间 dp。因为被炸掉的一定是连续的一段,所以 \(dp_{i,j}\) 只能从 \(dp_{i-1,j},dp_{i,j-1}\) 转移。类比 \(f\) 的转移即可。
模拟赛(晚上)
T1 \(90\) AC
观察数据范围,\(n1,n2\) 都比较小,于是可以考虑先算只有颜色 \(1,2\) 的个数,然后在相邻颜色相同的位置插入 \(3,4\)。
设 \(f_{i,j,k,l}\) 为 \(i,j\) 个颜色 \(1,2\),有 \(k\) 个位置相邻颜色一样,最后一个颜色为 \(l\)。通过 \(f\) 算出 \(g_i\),表示把 \(1,2\) 放完以后,有 \(i\) 个位置不合法的方案数。
这时候,\(3,4\) 有 \(i\) 个位置必须放,有 \(j(i\le j \le n_1+n_2+1)\) 个位置可以放。可以发现在每个空内,\(3,4\) 都有三种放法:\(3\) 比 \(4\) 多 \(1\),\(3=4\),\(3\) 比 \(4\) 少 \(1\),记作 ABA,AB,BAB。
枚举 ABA 的个数 \(k\),显然 BAB 的个数为 \(n4-n3+k\),那么 AB 的个数即为 \(j-ABA-BAB\)。
于是总方案数:
枚举 \(i,j,k\) 即可。
T2 \(80\)
原来写的笔记太烂了,索性直接删了。
T3 \(80\) AC
考虑算每个 \(a_i\) 对答案的贡献。
发现 \(a_i\) 与 \(a_{n-i+1}\) 的贡献是相同的,于是只需要算 \(i\le \lfloor \frac{n}{2} \rfloor\) 的 \(a_i\) 即可。
首先通过找规律预处理出来每个 \(a_i\) 的贡献,记作 \(v_i\),那么总贡献就是 \(\sum\limits_{i} a_iv_i\) 了。
用线段树维护一下这个东西就行了。
T4 \(20\) 没做
杂题
P3474
首先排除掉 \(> 2k\) 的点,如果有 \([k,2k]\) 之间的点,就在直接作为答案就行了。这时候矩阵中只剩下 \(<k\) 的点了。
通过[待填的]证明得出如果最大子矩阵 \(\ge k\) 则一定有解。[待填]。
一个指针随机地在一个 \(01\) 序列上瞬移,每次瞬移到的地方都把 \(01\) 取反,问期望多少次让这个序列变成全 \(0\) 或者全 \(1\)。
11.26
模拟赛
T1 \(100\) AC
二分两次即可。
T2 \(50\) AC
手模一下 \(n=2\) 的情况,发现 \(f(B,C)\) 与 \(f(A,C)\) 是有线性关系的,于是转化成二维平面上的问题。
在 \(n\ge 2\) 的情况下,所有 \((a_i,b_i)\) 这样的点可以构成 \(\frac{n(n+1)}{2}\) 条线段,可以发现答案一定在其中一条线段上。对于每个询问,枚举线段,然后算一下即可。
For(i,1,n){
if(a[i]>x) continue;
For(j,1,n){
if(i==j||a[j]<x) continue;
if(a[i]==a[j]) chkmax(ans,(double)max(b[i],b[j]));
else{
double k=(b[j]-b[i])/double(a[j]-a[i]),bb=b[j]-k*a[j];
chkmax(ans,k*x+bb);
}
}
}
printf("%.6lf\n",ans);
T3 \(100\) AC
赛时用 \(O(n^3 \log n)\) 的树状数组做法得了满分,但实际上有 \(O(n^3)\) 的做法。
T4 \(50\) TLE 90
考虑折半搜索。可以发现如果定了前 \(m\) 个空,那么可以计算出后面自身的逆序对数的范围。于是分成两半,先搜后面一半,再搜前面一半,但我的实现比较丑,死活卡不进最后一个点。
11.27
模拟赛(上午)
T1 \(100\) AC
略。
T2 \(100\) AC
略。
T3 \(60\)
考虑构造一个 \(n\times n\) 的矩阵 \(A\),其中 \(A_{i,j}\) 代表 \(a\) 的值为 \(i\),\(b\) 的值为 \(j\) 时的双色边数量。
发现每条边 \((u,v)\) 只会对 \(A\) 中的四个子矩阵造成影响,于是线段树模拟一下就行了。
T4 \(30\)
首先有一个十分 naive 的矩阵加速做法,做法显然,但和暴力一个分(\(60\))。
矩阵加速的一个条件是可以线性递推,但发现这东西其实可以倍增递推。设 \(f_{i,j}\) 为进行 \(i\) 轮,\(0\) 号在 \(j\) 的方案数,那么 \(f_{i_1,j_1}\times f_{i_2,j_2}\rightarrow f_{i_1i_2,(j_1+j_2)\bmod n}\)。倍增处理 \(f_{2^k}\),然后用类似快速幂的思想算 \(f_n\) 即可。
T3 \(30\)
\(30\) 分做法:设 \(f_{i,j}\) 为长为 \(i\) 的约数链,最后一个数为 \(j\) 的答案,枚举倍数, 进行刷表法即可。
发现 \(f_i\) 为积性函数,即如果 \(j,k\) 互质 则 \(f_{i,j}\times f_{i,k}=f_{i,jk}\)。
如何证明?当 \(j,k\) 互质,左边会有一些约数链,右边会有一些约数链,可以发现新的答案就是这些约数链两两相乘后相加. 用乘法分配律, 就可以证明了。
如果 \(j,k\) 不互质, 随便找组反例即可。
技巧:积性函数线性筛法。
代码:
#define ll long long
#define INF 0x3f3f3f3f
#define M 10000005
#define N 12
const int MOD=1000000007;
int n,m,prime[M],low[M],prCnt=0;ll f[M],dp[N][55];bool vis[M];
int main(){
scanf("%d%d",&n,&m);
f[1]=n;vis[1]=1;low[1]=1;
For(i,2,m){
if(!vis[i]){
low[i]=prime[++prCnt]=i;
//f[i]=(1LL*n*(n+1)/2*i%MOD+n*(n-1)/2)%MOD;
//memset(dp,0,sizeof dp);
ll p=1;
for(int k=0;p<=m;++k,p*=i){
dp[1][k]=p;
}
For(j,2,n){
p=1;ll s=0;
for(int k=0;p<=m;++k,p*=i){
s=(s+dp[j-1][k])%MOD;dp[j][k]=s*p%MOD;
}
}
p=1;
for(int k=0;p<=m;++k,p*=i){
f[p]=dp[n][k];
}
}
for(int j=1;j<=prCnt&&1LL*i*prime[j]<=m;++j){
vis[i*prime[j]]=1;
if(i%prime[j]==0){
low[i*prime[j]]=low[i]*prime[j];
if(low[i]!=i) f[i*prime[j]]=f[i/low[i]]*f[low[i]*prime[j]]%MOD;
break;
}
low[i*prime[j]]=prime[j];
f[i*prime[j]]=f[i]*f[prime[j]]%MOD;
}
}
ll ans=0;
//For(i,1,m) printf("%lld ",f[i]);
For(i,1,m) ans=(ans+f[i])%MOD;
printf("%lld\n",ans);
return 0;
}
T4 \(40\)
枚举一条删除的边, 设该图为 \(G\). 如果 \(G\) 不连通: \(ans=m(m-1)/2\).
否则, 找一棵 \(G\) 的 dfs 树. 此时, 有两种删边方法:
-
删去一条树边+一条非树边.
此时, 枚举树边, 如果这条树边不被任何非树边覆盖, 则任意选非树边即可. 如果只被一条非树边覆盖, 也是合法的. 否则无解.
-
删去两条树边.
此时, dfs 一下这棵 dfs 树, 对于每条边, 使用类似哈希的方法算出有哪些非树边覆盖了树边 \((u,v)\), 记作 \((u,v)\) 的权值. 因为必须在删掉这两条树边之后不连通, 所以只有两个权值相同的边能够被删除.
11.29
模拟赛
T2
枚举人的编号 \(i\),对于长度 \(\ge i\) 的区间,至少会覆盖一次,反之,最多会覆盖一次。于是树状数组统计即可,时间复杂度 \(O(m \log^2 m)\)。


