modeling probabilities and nonlinearities: activation functions （Grokking 第九章学习笔记）

为什么需要激活函数？

在Grokking书中之前的章节，我们学会了如何搭建一个如下所示的、简单的神经网络，并根据输出数据做出预测。

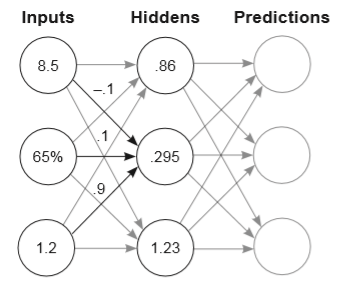
很容易可以看出：隐藏层神经元的值，是对应的输入层神经元乘以权重后的累加和。同理，输出层神经元的值也是如此。

这就导致了一个问题：不管隐藏层如何叠加，最终的预测结果总是输入值的线性表示。

在具体的场景中，这个问题更加的直观。比如在下图所示的分类问题中，我们可以很容易的找到一条线段完成分类操作：

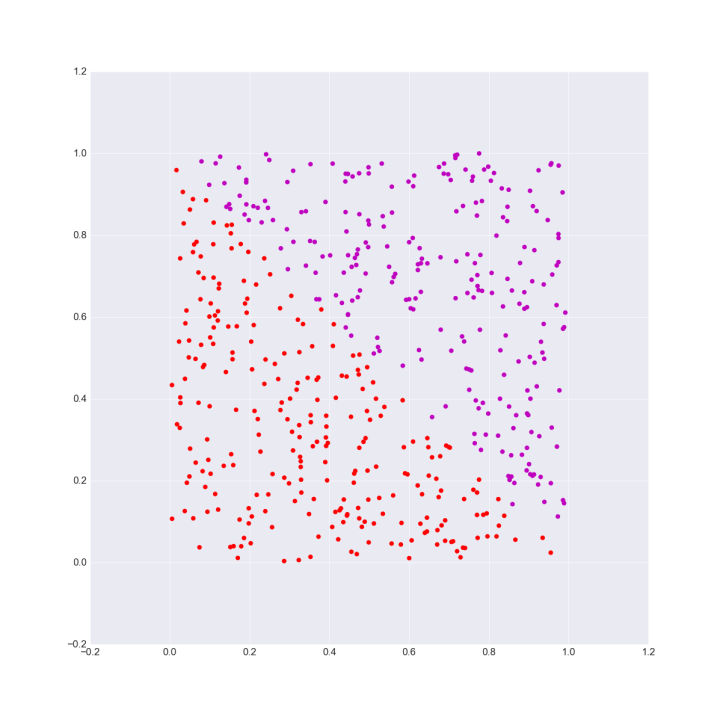
但是在处理类似异或等问题时，我们始终不能用一条线段来完成分类

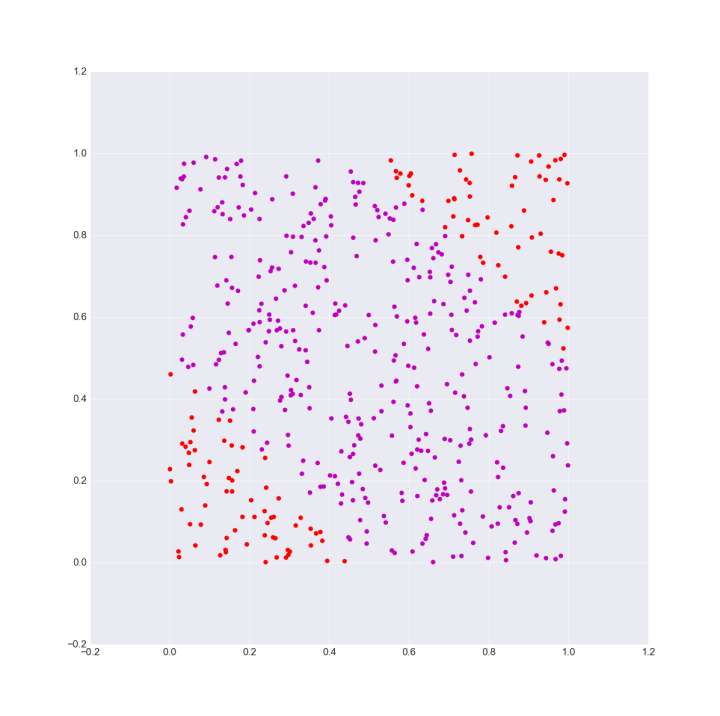
为了解决类似的问题，我们在神经网络中引入激活函数，使得最终的预测结果与输入值之间的关系变成非线性关系。

 

激活函数的性质

首先激活函数必须是连续的，在这里先复习以下函数连续的概念：

　　设函数 y = f (x)在点x0的某邻域内有定义，如果当自变量的改变量△x趋近于 零时，相应函数的改变量△y也趋近于零，则称y = f (x)在点 x0处连续

　　

　　也就是说，如函数y = f (x)在点x0出连续时满足下列条件：

　　　　函数在该点处有定义；函数在该点出的极限存在且极限值等于函数值

另一方面，激活函数的输入域应该是无限，你要保证对于任意的x值激活函数都由相对应的映射值。

 

什么是一个好的激活函数？

首先一个好的激活函数应该是单调的，如下图所示的激活函数就并非一个优秀的激活函数，因为在神经网络中绝大多数情况下不同的两个x值对应相同的y值是没有意义的。

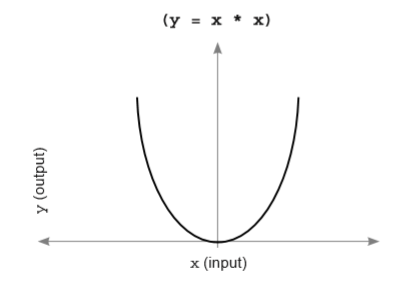
其次，一个好的激活函数应当是非线性的（不然我引入吔屎吗？）

最后，一个好的激活函数及其派生函数应该是可以被有效计算的（这里的有效计算指计算的时间复杂度是多项式复杂度）

 

常用的激活函数

一、Sigmoid函数

　　sigmoid函数即 S(x) = 1/(1+exp(-x))

　　

　sigmoid函数的缺点在于：函数并非关于原点中心对称，同时可以很直观的看出，在|x|趋近于无穷时，会’杀死梯度‘。

二、Tanh函数

　　tanh函数即 T(x) = (exp(x)-exp(-x))/(exp(x)+exp(-x))

　　

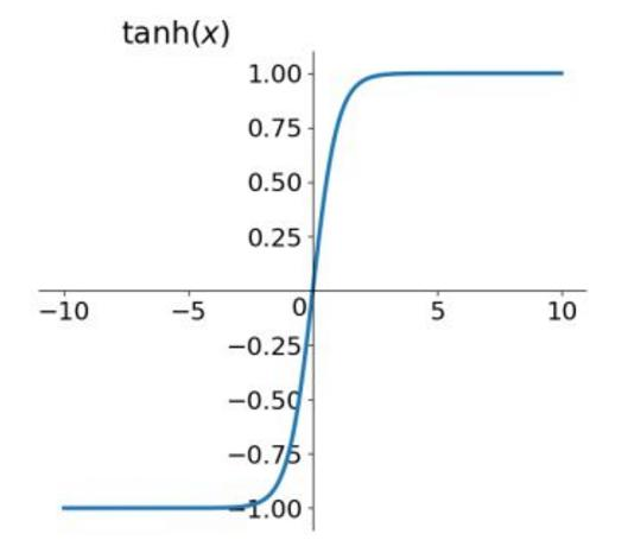
　　tanh函数解决了sigmoid函数不关于原点中心对称的问题，但是梯度消失的现象依然存在

三、Relu函数

　　relu函数即 R(x) = max(0,x)

　　

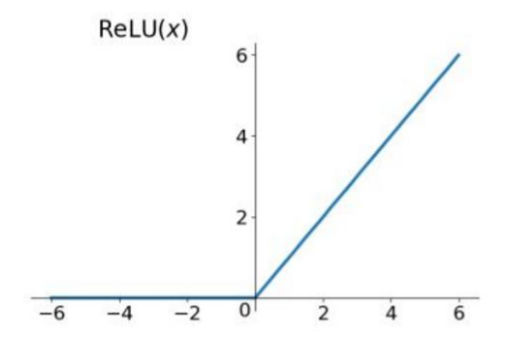
　relu函数解决了梯度消失的问题，同时计算效率极高。

　其缺点在于relu函数会杀死部分神经元。这个问题可以被Leaky ReLU函数解决，Leaky ReLU函数为：LR(x) = max(0.01x,x)