ioi1998 Polygon
题目描述
多边形是一个玩家在一个有n个顶点的多边形上的游戏,如图所示,其中n=4。每个顶点用整数标记,每个边用符号+(加)或符号*(乘积)标记。
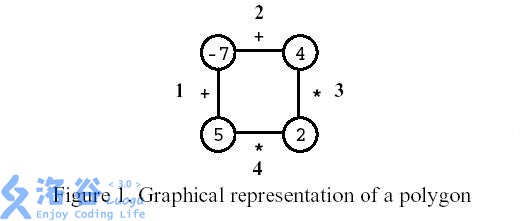
第一步,删除其中一条边。随后每一步:
选择一条边连接的两个顶点V1和V2,用边上的运算符计算V1和V2得到的结果来替换这两个顶点。
游戏结束时,只有一个顶点,没有多余的边。
如图所示,玩家先移除编号为3的边。之后,玩家选择计算编号为1的边,然后计算编号为4的边,最后,计算编号为2的边。结果是0。
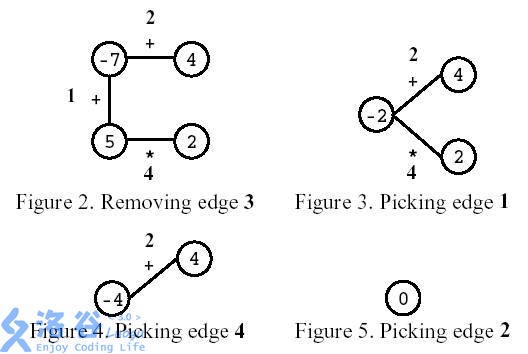
编写一个程序,给定一个多边形,计算最高可能的分数。
输入格式
输入描述一个有n个顶点的多边形,它包含两行。第一行是数字n,为总边数。
第二行描述这个多边形,一共有2n个读入,每两个读入中第一个是字符,第二个是数字。
第一个字符为第一条边的计算符号(t代表相加,x代表相乘),第二个代表顶点上的数字。首尾相连。
3 < = n < = 50
对于任何一系列的操作,顶点数字都在[-32768,32767]的范围内。
输出格式
第一行,输出最高的分数。在第二行,它必须写出所有可能的被清除后的边仍能得到最高得分的列表,必须严格递增。
我们想不到任何删边的贪心做法,所以先考虑枚举删哪条边。
删去一条边后,由于每次操作等于把左边和右边合并起来,所以我们可以考虑区间dp。设dp(l,r)表示区间l,r可以得到的最大分值,但是问题就来了:
计算时可能出现负数,可能两个很小的负数相乘之后可以得到更大的分值。
所以我们的状态还不够。设dp(l,r,0/1)表示l~r的最大分值(1)和最小分值(0)。那么可以得出状态转移方程:
\[dp[l][r][1]= \left\{ \begin{array}{rcl}
Max_{l≤k<r}{\{}Max_{0≤x≤1,0≤y≤1}{\{}dp[l][k][x]*dp[k+1][r][y]{\}} & c[k+1]=x\\
Max_{l≤k<r}{\{}dp[l][k][1]+dp[k+1][r][1]{\}} & c[k+1]=t
\end{array}\right.\\
dp[l][r][0]= \left\{ \begin{array}{rcl}
Min_{l≤k<r}{\{}Min_{0≤x≤1,0≤y≤1}{\{}dp[l][k][x]*dp[k+1][r][y]{\}} & c[k+1]=x\\
Min_{l≤k<r}{\{}dp[l][k][0]+dp[k+1][r][0]{\}} & c[k+1]=t
\end{array}\right.
\]
初始化dp(i,i,0/1)=val(i),其余等于-inf。
时间复杂度为O(N^4)。
回想上面的具体实现方式,我们需要断掉一条边之后把整个环变成一条链,然后再进行dp。其余不说,反正我是觉得很难写。
对于断环成链的地方,我们没必要每断一次都处理一遍剩余部分。我们可以预处理时就断开环,然后复制一份接在后面。那么我们如果要删第i个位置,我们则直接在i~i+n的位置上dp即可。所以我们在枚举区间长度时将长度控制在n以内,通过区间dp算出每一个长度为n的区间的最优值,最后答案就是Max{dp(i,i+n-1,1)}。
时间复杂度为O(2N * N2)=O(N3)。
#include<iostream>
#include<cstring>
#include<cstdio>
#define maxn 51
using namespace std;
int dp[maxn<<1][maxn<<1][2];
int n,eval[maxn<<1],vval[maxn<<1];
int ans=-0x3f3f3f3f,res[maxn],d;
inline int read(){
register int x(0),f(1); register char c(getchar());
while(c<'0'||'9'<c){ if(c=='-') f=-1; c=getchar(); }
while('0'<=c&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
int main(){
n=read();
for(register int i=1;i<=n;i++){
char op; cin>>op;
eval[i]=eval[i+n]=(op=='t'),vval[i]=vval[i+n]=read();
}
for(register int i=1;i<=n<<1;i++){
for(register int j=1;j<=n<<1;j++) dp[i][j][0]=0x3f3f3f3f,dp[i][j][1]=-0x3f3f3f3f;
}
for(register int i=1;i<=n<<1;i++) dp[i][i][0]=dp[i][i][1]=vval[i];
for(register int len=2;len<=n;len++){
for(register int l=1,r=len;r<=n<<1;l++,r++){
for(register int k=l;k<r;k++){
if(!eval[k+1]){
dp[l][r][1]=max(dp[l][r][1],max(dp[l][k][0]*dp[k+1][r][0],max(dp[l][k][0]*dp[k+1][r][1],max(dp[l][k][1]*dp[k+1][r][0],dp[l][k][1]*dp[k+1][r][1]))));
dp[l][r][0]=min(dp[l][r][0],min(dp[l][k][0]*dp[k+1][r][0],min(dp[l][k][0]*dp[k+1][r][1],min(dp[l][k][1]*dp[k+1][r][0],dp[l][k][1]*dp[k+1][r][1]))));
}else{
dp[l][r][1]=max(dp[l][r][1],dp[l][k][1]+dp[k+1][r][1]);
dp[l][r][0]=min(dp[l][r][0],dp[l][k][0]+dp[k+1][r][0]);
}
}
}
}
for(register int i=1;i<=n;i++) ans=max(ans,dp[i][i+n-1][1]);
printf("%d\n",ans);
for(register int i=1;i<=n;i++) if(ans==dp[i][i+n-1][1]) printf("%d ",i);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号