[Noip2018]旅行
题目描述
小 Y 是一个爱好旅行的 OIer。她来到 X 国,打算将各个城市都玩一遍。
小Y了解到, X国的 n个城市之间有 m条双向道路。每条双向道路连接两个城市。 不存在两条连接同一对城市的道路,也不存在一条连接一个城市和它本身的道路。并且, 从任意一个城市出发,通过这些道路都可以到达任意一个其他城市。小 Y 只能通过这些 道路从一个城市前往另一个城市。
小 Y 的旅行方案是这样的:任意选定一个城市作为起点,然后从起点开始,每次可 以选择一条与当前城市相连的道路,走向一个没有去过的城市,或者沿着第一次访问该 城市时经过的道路后退到上一个城市。当小 Y 回到起点时,她可以选择结束这次旅行或 继续旅行。需要注意的是,小 Y 要求在旅行方案中,每个城市都被访问到。
为了让自己的旅行更有意义,小 Y 决定在每到达一个新的城市(包括起点)时,将 它的编号记录下来。她知道这样会形成一个长度为 n的序列。她希望这个序列的字典序 最小,你能帮帮她吗? 对于两个长度均为 n的序列 A和 B,当且仅当存在一个正整数 x,满足以下条件时, 我们说序列 A的字典序小于 B。
对于任意正整数 1 ≤ i < x,序列 A的第 i个元素 A_i和序列 B的第 i个元素 B_i相同。
序列 A的第 x个元素的值小于序列 B的第 x个元素的值。
输入格式
输入文件共 m + 1行。第一行包含两个整数 n,m(m ≤ n),中间用一个空格分隔。
接下来 m 行,每行包含两个整数 u,v (1 ≤ u,v ≤ n),表示编号为 u和 v的城市之 间有一条道路,两个整数之间用一个空格分隔。
输出格式
输出文件包含一行,n个整数,表示字典序最小的序列。相邻两个整数之间用一个 空格分隔。
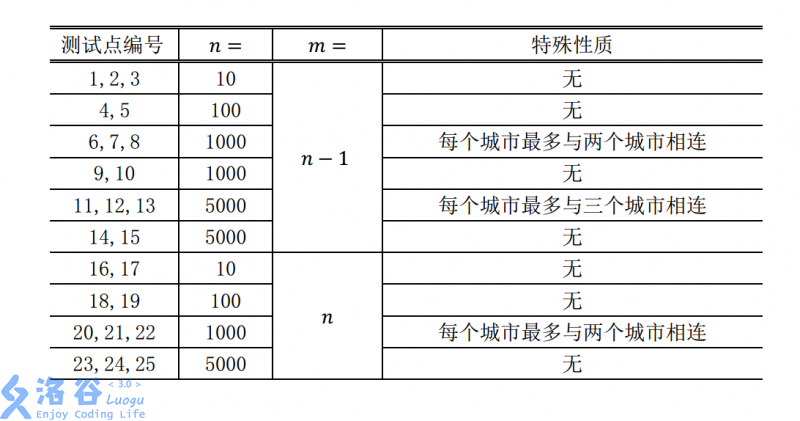
首先贪心思路很容易想。
假设当前可以走到u,v两个点,其中u的字典序小于v的字典序,我们显然应该直接走u。因为如果走了v,那么之后再怎么走也走不出比走u字典序更小的路径了。可以从两个点拓展到更多的点。
所以总结一下,我们的贪心策略就是——走当前点连出去的字典序最小的点。
那么你前15组数据稳稳地过了。但后面的就有点不一样——基环树!那这个基环树就把问题搞得复杂了。
根据题意,我们在走到环上时,我们可以往左走或者往右走。根据我们的贪心策略,我们往字典序小的一边走。这里假设我们往左走。但是题目中说了,我们是可以往回走的,这个条件在基环树上回发生什么化学反应呢?显然,我们往左走了若干个点后,我们发现这个字典序还是挺大的,这时我们可以后悔一次!然后退回环的起始点,往右走,从而得到更优的解。那么例子也是很好举的,样例2就有一个:
Sample in
6 6
1 3
2 3
2 5
3 4
4 5
4 6
Sample out
1 3 2 4 5 6
这种后悔的操作可以怎么理解呢?首先你面前有一个环上的点,你本来要走过去,但是你没走。这可以理解为把你和你面前的点之间的边断掉了。所以我们的核心思路就是——断边。我们可以先找出环,然后枚举环上的每条边,把它断掉,然后根据前60分的贪心思路跑一遍。重复跑了若干次后,我们去最优解即可。时间复杂度O(N^2),再一看数据,加点小小的常数优化(代码中标出)是可以过的。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<map>
#define maxn 5001
using namespace std;
vector<int> to[maxn];
int dfn[maxn],fa[maxn],tot,s;
bool inloop[maxn];
pair<int,int> del1,del2;
int n,m;
int ans[maxn],path[maxn],d;
map<pair<int,int>,bool> use;
inline int read(){
register int x(0),f(1); register char c(getchar());
while(c<'0'||'9'<c){ if(c=='-') f=-1; c=getchar(); }
while('0'<=c&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
//基环树的情况
void dfs_getloop(int u){
dfn[u]=++tot;
for(register int i=0;i<to[u].size();i++){
int v=to[u][i];
if(!dfn[v]) fa[v]=u,dfs_getloop(v);
else if(dfn[u]<dfn[v]){
inloop[v]=true;
do{ inloop[fa[v]]=true,v=fa[v]; }while(v!=u);
}
}
}
void dfs(int u,int pre){
path[++d]=u;
if(inloop[u]&&!s) s=u;
for(register int i=0;i<to[u].size();i++){
int v=to[u][i];
if(v==pre||v==s) continue;
if(make_pair(u,v)==del1||make_pair(u,v)==del2) continue;
dfs(v,u);
}
}
inline void cmp(){//比较答案
for(register int i=1;i<=n;i++){
if(path[i]<ans[i]) break;
if(path[i]>ans[i]) return;
}
for(register int i=1;i<=n;i++) ans[i]=path[i];
}
//树的情况
void dfs2(int u,int pre){
ans[++d]=u;
for(register int i=0;i<to[u].size();i++){
int v=to[u][i];
if(v==pre) continue;
dfs2(v,u);
}
}
int main(){
n=read(),m=read();
for(register int i=1;i<=m;i++){
int u=read(),v=read();
to[u].push_back(v),to[v].push_back(u);
}
//按字典序排序,实际上这里用基排可以做到O(N)
for(register int i=1;i<=n;i++) sort(to[i].begin(),to[i].end());
if(m==n){
dfs_getloop(1);
memset(ans,0x3f,sizeof ans);
for(register int i=1;i<=n;i++) if(inloop[i]){
for(register int j=0;j<to[i].size();j++){
int v=to[i][j];
if(inloop[v]&&!use[make_pair(i,v)]){
d=s=0,del1=make_pair(i,v),del2=make_pair(v,i);//断掉双向边
use[make_pair(i,v)]=true,use[make_pair(v,i)]=true;//这里用map记一下可以把我们的遍历次数减半
dfs(1,0),cmp();
}
}
}
}else dfs2(1,0);
for(register int i=1;i<=n;i++) printf("%d ",ans[i]);puts("");
return 0;
}
显然我们的做法太暴力了,然后有人做了个这道题的加强版数据,n≤500000。经过分析和打表发现,我们所有删边的操作中好像也就只有那一次可以得到正解,所以我们要想办法得到这条边。
我们回想一下我们删边的原因:退回去换一个方向走的答案比继续往下走更优。这里我们注意到,我们退回去时并不是直接退回到环的起始点,而是在往回走的每个点上把没走过的地方走完了才继续往回走。而走没走过的地方显然也需要遵循我们的贪心策略。那么什么时候往回走会更优呢?假设我们最近的一个还有地方没走的祖先是u,它的没走过的字典序最小的儿子为son(u),当前点为v,当前点的下一个在环上的点为son(v),那么显然只有当son(u)<son(v)时往回走会更优——参照贪心的思路。所以我们只需要记下这个u即可。
不过我们还有需要注意的地方:
我们走的时候只能后悔一次。
只有当当前点的其它儿子都走过了时才可以选择后悔。
时间复杂度为O(NlogN)。但由于本人写法的原因(给儿子排序的部分),本人代码的实际复杂度其实是
\[O(N*\sum_{i=1}^{N}log_{2}Degree[i])
\]
可以发现增长率是很大的,但它确实是nlogn级别。不过在luogu开了O2可以过。
*degree表示这个点的度数
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
#define maxn 500001
using namespace std;
vector<int> to[maxn];
int dfn[maxn],fa[maxn],tot;
bool inloop[maxn],vis[maxn],flag;
int n,m;
int ans[maxn],d;
inline int read(){
register int x(0),f(1); register char c(getchar());
while(c<'0'||'9'<c){ if(c=='-') f=-1; c=getchar(); }
while('0'<=c&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
void dfs_getloop(int u){
dfn[u]=++tot;
for(register int i=0;i<to[u].size();i++){
int v=to[u][i];
if(!dfn[v]) fa[v]=u,dfs_getloop(v);
else if(dfn[u]<dfn[v]){
inloop[v]=true;
do{ inloop[fa[v]]=true,v=fa[v]; }while(v!=u);
}
}
}
void dfs(int u,int fa,int pre){
if(vis[u]) return;
ans[++d]=u,vis[u]=true;
priority_queue< int,vector<int>,greater<int> > q;
for(register int i=0;i<to[u].size();i++) if(!vis[to[u][i]]||to[u][i]!=fa) q.push(to[u][i]);
//换成这种写法的原因是为了更好地判断环上的下一个点不是自己的父亲
while(q.size()){
int v=q.top(); q.pop();
if(inloop[v]&&v>pre&&!q.size()&&!flag){ flag=true; return; }
if(inloop[v]&&q.size()) dfs(v,u,q.top());
else dfs(v,u,pre);
}
}
int main(){
n=read(),m=read();
for(register int i=1;i<=m;i++){
int u=read(),v=read();
to[u].push_back(v),to[v].push_back(u);
}
if(m==n) dfs_getloop(1);
dfs(1,0,0x3f3f3f3f);
for(register int i=1;i<=n;i++){
if(i!=1) putchar(' ');
printf("%d",ans[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号