与数论的厮守02:整数的因子分解—Pollard_Rho
学Pollard_Rho之前,你需要学会:Miller Rabin。
这是一个很高效的玄学算法,用来对大整数进行因数分解。
我们来分解n。若n是一个素数,那么就不需要分解了。所以我们还得能够判断一个数是否为素数才行。而n是个大整数,显然普通的试除法和筛法都是不够它跑的。所以我们就得考虑用Miller Rabin来判断。
但n不是素数呢?这就得用Pollard_Rho了。首先我们来看一个有趣的东西:生日悖论。
生日悖论:说简单点,就是在N个数里面选k个,当k接近√N时,选出两个相同数的几率约为50%。比如,不考虑闰年时,一个班若有23个人,则有两人生日相同的概率约为50%;但人数达到60时,概率约为基本上就是100%了,这严重违背了我们的生活经验,所以被列为了悖论。
模仿着生日悖论,若在1~N里面选k个数X1,X2...XK,若k足够大,则很大几率有gcd(Xi-Xj,N)>1,也就是二者不互质,此时gcd(Xi-Xj,N)就是N的一个因数了。但是这样做复杂度又退回了O(k2),处理不好还能退化为O(n2)。所以Pollard_Rho是有改进的。首先是空间。改进的Pollard_Rho只需要存相邻的两个数:Xi,Xi+1。同时为了得到这些数,Pollard_Rho还设计了一个函数:f(Xi)=(Xi2+c) mod n。这个c可以rand出来。然后再计算d=gcd(|Xi-Xi+1|,N),若d>1,则递归分解d和n/d。
但是mod n的值∈[0,n-1]之间,只有n个数,所以当递归够深时就会出现循环,这不利于我们的算法。就是这个样子(图是盗的):
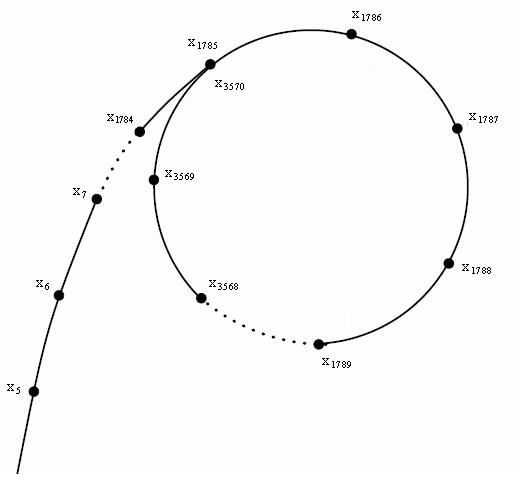
这里就有一个优化。像刚才的图一样,我们可以把循环节看成是一个环,我们只需要找出环就可以停下了。不然就一直跑到递归的数为素数为止。怎么找环呢?我们会想一下小学的追及问题。假设跑道上有两个人,一个高个子和一个矮个子。矮个子的速度为1,高个子的速度为2。如果跑道是无限长的直线,那高个子就会永远跑在矮个子前面。但如果有环,那么高个子就肯定追得到矮个子。Pollard_Rho就可以用这个办法来找环。

(这个图也是盗的)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号