【数值计算方法】常微分方程数值解-数值实验

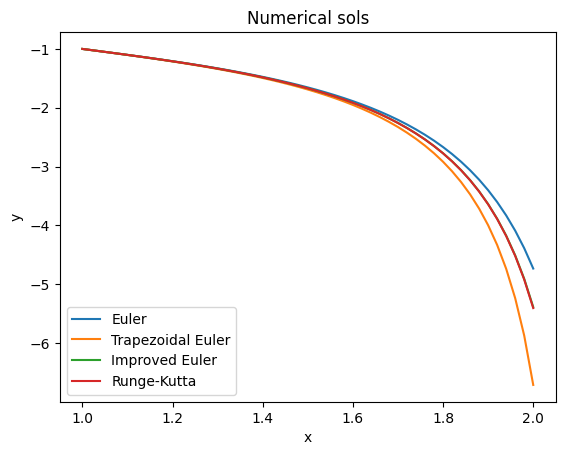
第一题

y=y(x)的数值解

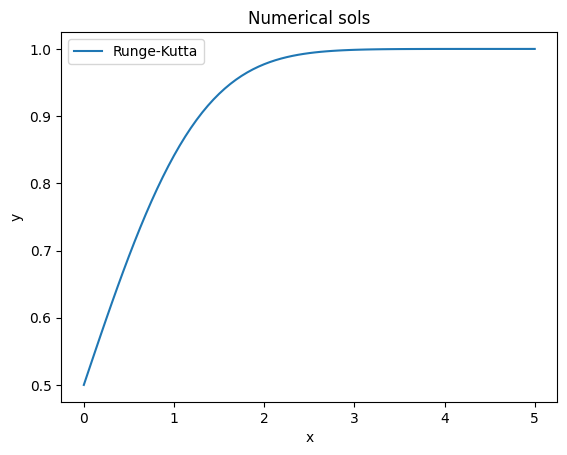
第二题

\(x-\varPhi(x)\)的数值解

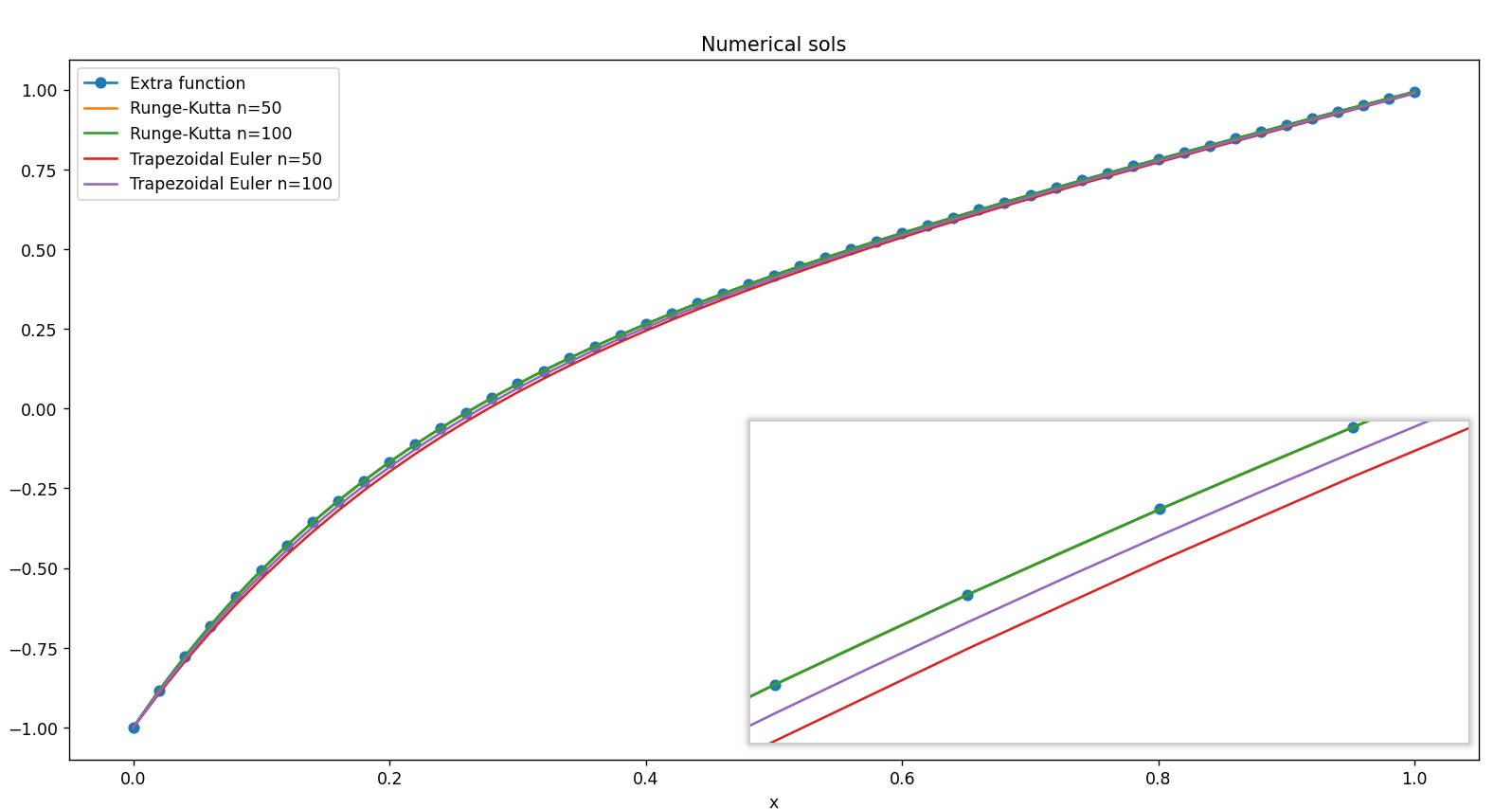
第三题

在梯形公式中当采用简单迭代格式求解y_{n+1}时,h=0.2,0.25步长过大.

题中t为x,数值解为:

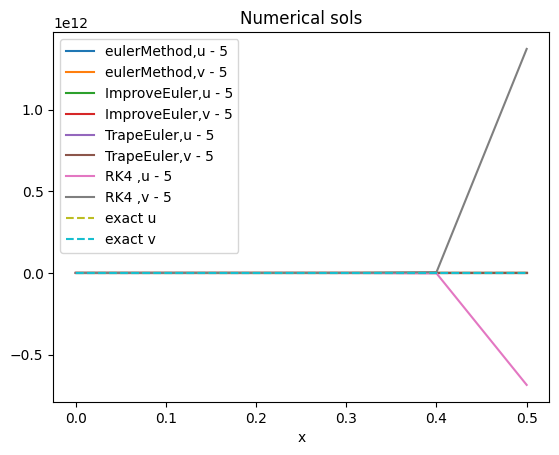
第四题

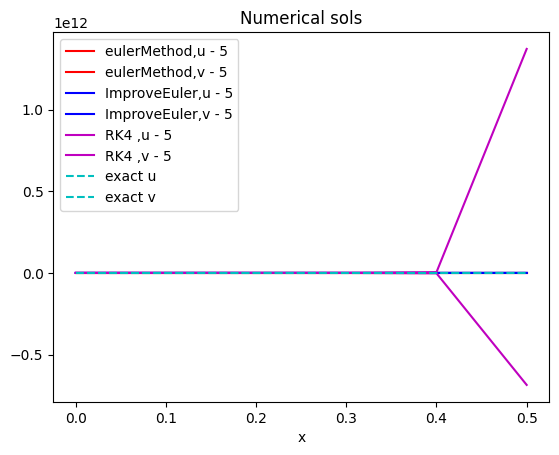
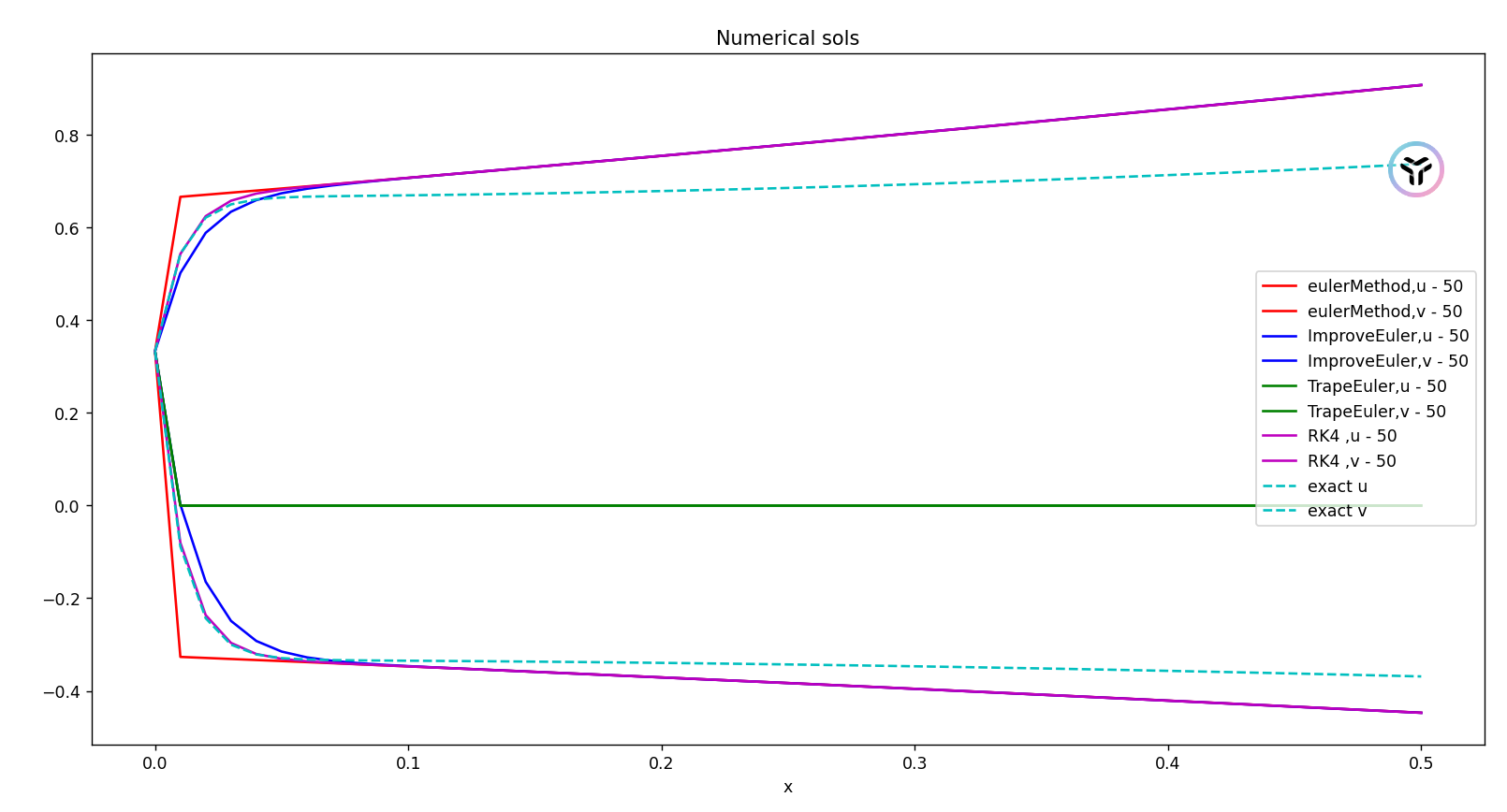
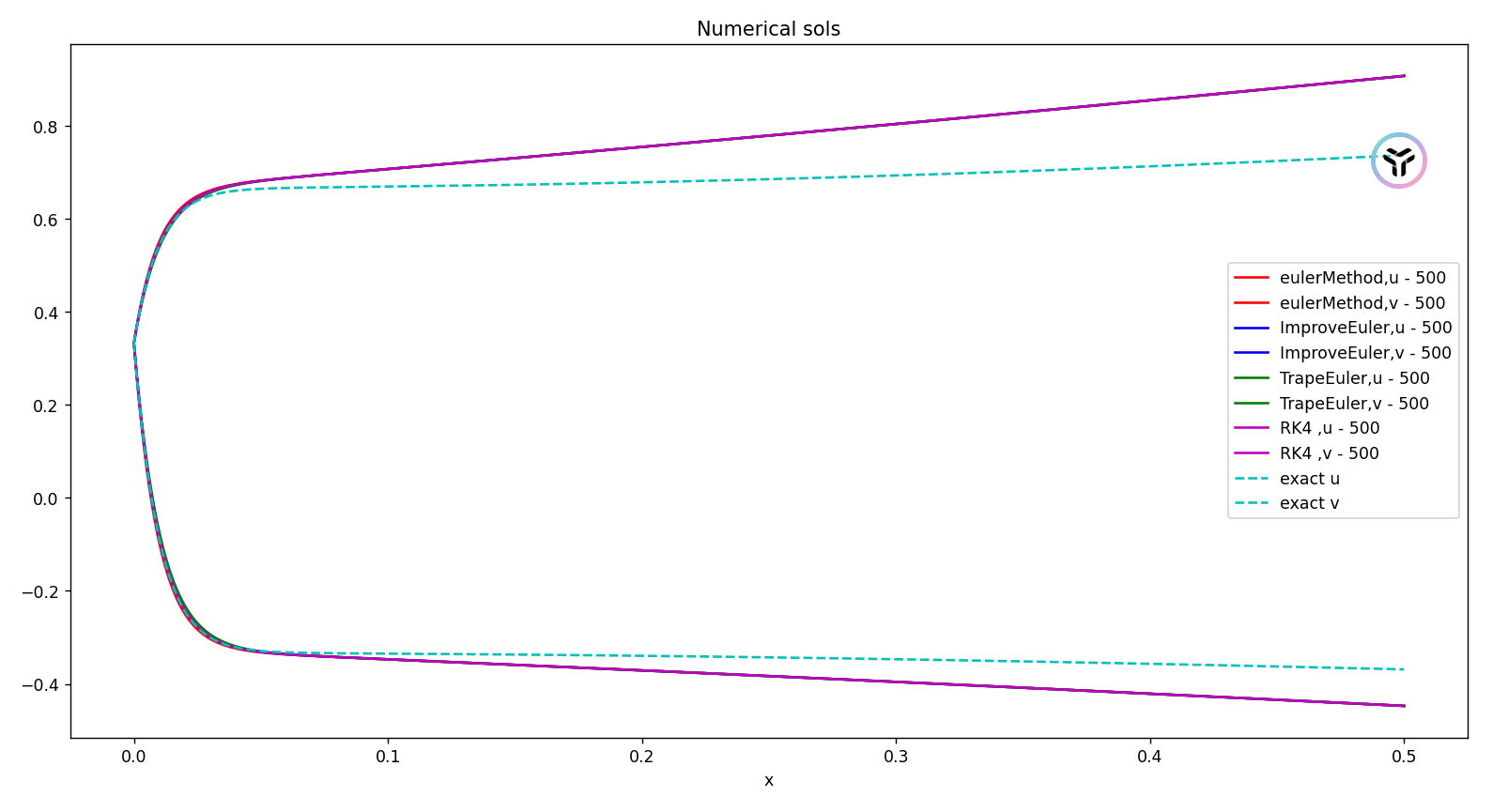
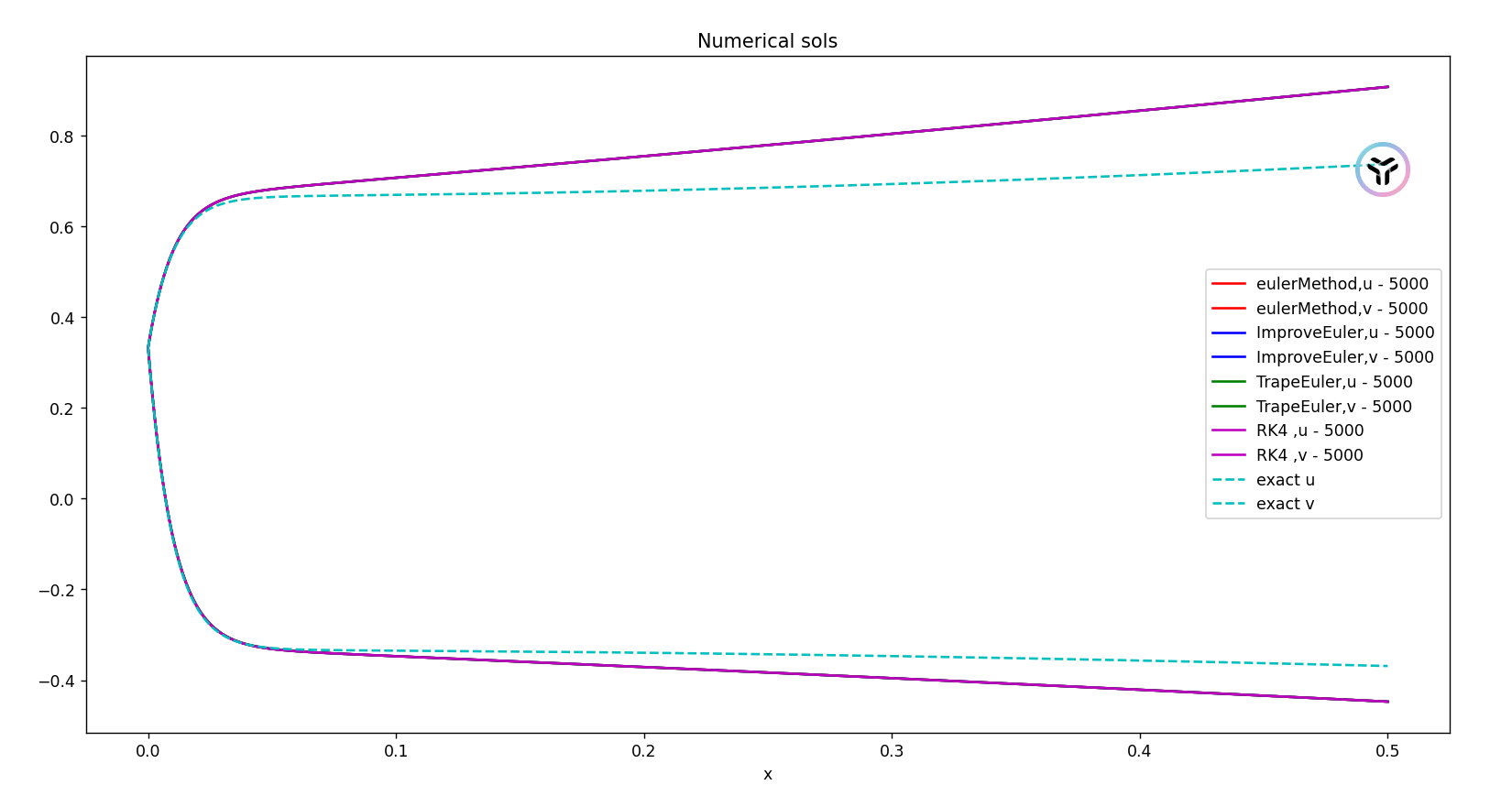
采用欧拉公式,改进欧拉公式,4阶龙格库塔公式,梯形公式求解y(x)的数值解,对比精度.

n=5:

n=50:

n=500:

n=5000:

code

# %%
from formu_lib import *
import numpy as np
import matplotlib.pyplot as plt
 
def f(x:float,y:float)->float:
    return -1/(x*x)-y/x-y**2
 
y0,a,b,n=-1,1,2,50
x1,y1=EulerMethod(f,y0,a,b,n)
x2,y2=TrapeEuler(f,y0,a,b,n)
x3,y3=ImproveEulerMethod(f,y0,a,b,n)
x4,y4=RungeKuttaMethods(f,y0,a,b,n)
 
plt.plot(x1,y1,label='Euler')
plt.plot(x2,y2,label='Trapezoidal Euler')
plt.plot(x3,y3,label='Improved Euler')
plt.plot(x4,y4,label='Runge-Kutta')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Numerical sols')
plt.legend()
plt.show()
 
# %%
from formu_lib import *
import numpy as np
import matplotlib.pyplot as plt
 
def f2(x:float,y:float)->float:
    def phi(t:float)->float:
        return np.exp(-t*t/2.0)
    return (1/np.sqrt(2*np.pi))*Integ1dGuassLegendre(phi,0,x)+0.5
    
y0,a,b,n=0.5,0,5,80
h=(b-a)/n
x21=[a+i*h for i in range(n+1)]
y21=[]
for x in x21:
    y21.append(f2(x,y0))
 
plt.plot(x21,y21,label='Runge-Kutta')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Numerical sols')
plt.legend()
plt.show()
 
# %%
from formu_lib import *
import numpy as np
import matplotlib.pyplot as plt
 
def f3(x:float,y:float)->float:
    return (5.0*np.exp(5*x))*(y-x)*(y-x)+1.0
 
def extra_f3(x:float)->float:
    return x-np.exp(-5*x)
 
y0,a,b=-1,0,1.0
n1,n2=50,100
h=(b-a)/n1
x=[a+i*h for i in range(n1+1)]
y=[extra_f3(x[i]) for i in range(n1+1)]
plt.plot(x,y,label='Extra function',marker='o')
 
x31,y31=RungeKuttaMethods(f3,y0,a,b,n1)
x32,y32=RungeKuttaMethods(f3,y0,a,b,n2)
x33,y33=TrapeEuler(f3,y0,a,b,n1)
x34,y34=TrapeEuler(f3,y0,a,b,n2)
 
plt.plot(x31,y31,label=f'Runge-Kutta n={n1}')
plt.plot(x32,y32,label=f'Runge-Kutta n={n2}')
plt.plot(x33,y33,label=f'Trapezoidal Euler n={n1}')
plt.plot(x34,y34,label=f'Trapezoidal Euler n={n2}')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Numerical sols')
plt.legend()
plt.show()