【数值计算方法】常微分方程初值问题的数值解
常微分方程初边值问题数值解
第九章
1. 引言
微分方程 :含有未知函数及其导数或微分的等式;
除了少数特殊类型的微分方程能用解析方法求得精确解外 , 多数情况找不到解的解析表达式
本章研究两类常微分问题: 一阶常微分方程的初值问题 ; 两阶常微分方程边值问题
- 一阶常微分方程的初值问题
\(y(x)\) 是定义在 [a,b] 上的 m 维函数向量; \(f(x,y)\) 是定义在 m + 1 维区域\(G=\{(x,\boldsymbol{y})\mid x\in[a,b],\boldsymbol{y}\in\mathbb{R}^m\}\) 上的 m 维已知函数向量.
由常微分方程理论知:如果函数 f(x,y) 在区域 G 中连续 , 且关于y 满足利普希茨 (Lipschitz) 条件 , 即对所有\(x\in[a,b]\text{ 及 }y\in\mathbb{R}^m, z\in\mathbb{R}^m,\) 总存在常数 L > 0,使得:
则方程 (9.1) 存在唯一解 , 且解连续依赖于初始条件和右端项
- 两阶常微分方程边值问题
其中 \(q(x)\) 和 \(f(x)\) 在区间 [a,b] 上连续 , q(x) > 0. 这里假设上述边值问题存在唯一解 , 且解连续依赖于边界条件和右端项
- 总结
无论是初值问题还是边值问题 , 其解 \(\boldsymbol{y}=\boldsymbol{y}(x)\) 都是区间 [a,b] 上关于变量 x 的函数或函数向量,\(\boldsymbol{y}=(y_1(x),y_2(x),\cdots,y_m(x))^T\). 记 \(a=x_{0}<x_{1}<\cdots<x_{N-1}<x_{N}=b\) 为求解区域中的一系列节点 . 数值解就是要计算精确解 \(\boldsymbol{y(x)}\) 在这些节点 \(x_n\) 处的近似值 \(\boldsymbol{y_n}\) .
为了简单起见,假设网格点为均匀网格:
h为网格步长,本文主要介绍 m = 1 时的初值问题 , 对于边值问题和 m > 1 的情况下的初值问题将分别在最后两节作简单介绍
2.欧拉公式(欧拉折线法)
初值问题:
欧拉公式是求解初值问题 公式(1) 的一种简单而古老的数值方法 .
- 基本思路
把方程(1) 中的导数项 \(\boldsymbol{y'}\) 用差商逼近 , 从而把一个微分方程转化成为一个代数方程 , 以便求解.
在节点\(x_n\)处, 公式(1)有:
\(y'\)有三种差商公式:前向差商, 后向差商, 中间差商.以下以前向差商为例:
则得到离散公式:
因为真解 y(x) 是未知的, 所以用近似解 y(x_n) 来逼近真解.只要知道初值\(y(a)=y_0\), 就可以用欧拉公式来求解出\(y(x_i),i=1,2,\cdots,n\)的数值解.
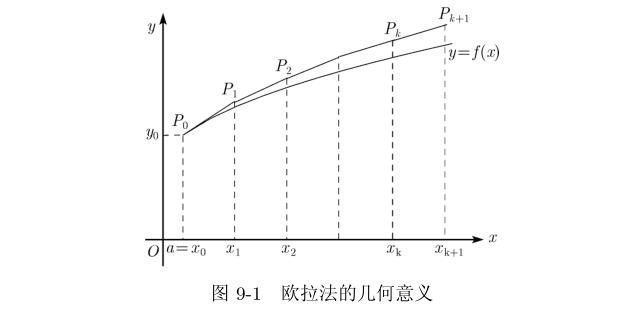
欧拉公式的几何意义十分清楚,方程 \(y' = f(x,y)\) 满足初始条件 \(y(x_0 ) = y _0\) 的解y = y(x) 是 xOy 平面上过点 \(P_0 (x_0 ,\boldsymbol{y_0})\) 的一条特殊积分曲线.欧拉方法就是用从 \(P_0\) 出发的折线 \(P_0, P_1 ···P_N\) 来作为积分曲线 y = y(x) 的近似解

2.1 例题

精确解:\(y(x)=\sqrt{1+2x}\)
# -*- coding: utf-8 -*-
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
def f(x,y)->float:
return y-2*x/y
y0,a,b,n=1,0,1,10
def y(x)->float:
return np.sqrt(1+2*x)
xi,yi=EulerMethod(f,y0,a,b,n)
plt.plot(xi,yi,label='Euler Method')
plt.plot(xi,[y(i) for i in xi],label='Exact Solution')
plt.legend()
plt.show()
plt.plot(xi,[abs(yi[i]-y(xi[i])) for i in range(len(yi))],label='Absolute Error')
plt.legend()
plt.show()
- 数值解和精确解的对比
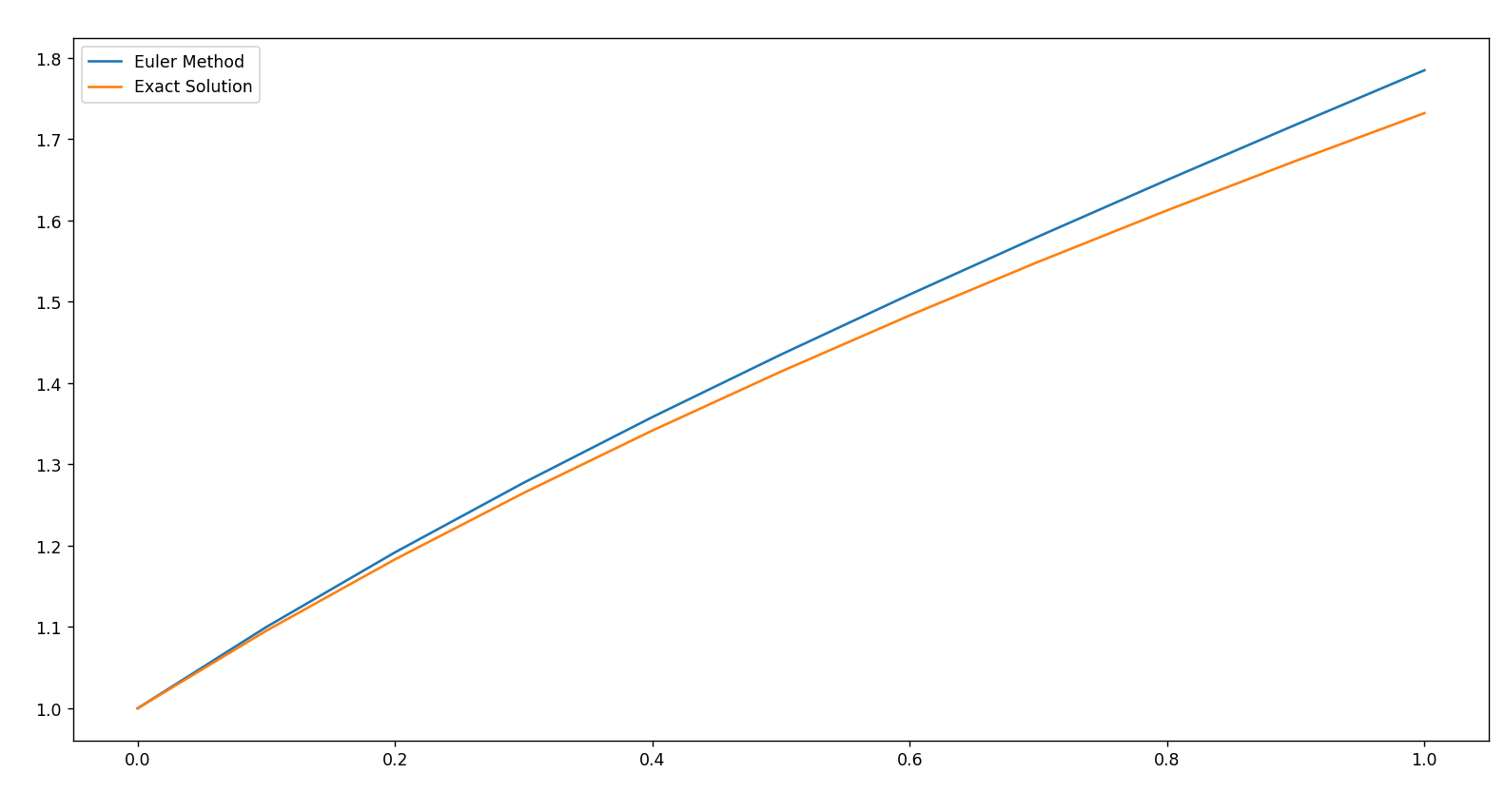

两者相比较 , 显然欧拉方法给出的数值解误差较大 , 一般只有两位有效数字
3. 欧拉公式的改进
从另一角度来考察初值问题,(1) 式改写为:
令积分区间为\([x_n,x_{n+1}]\),则有:
积分式如下:
对于右端的积分式子,其中含有位置函数y(x),无法直接计算,可以采用数值积分的方法计算其近似值.将初值问题方程 (1) 离散化的方法称为初值问题的数值积分方法
使用不同的数值积分公式,会有不同的计算公式
若采用左矩形积分公式,则:
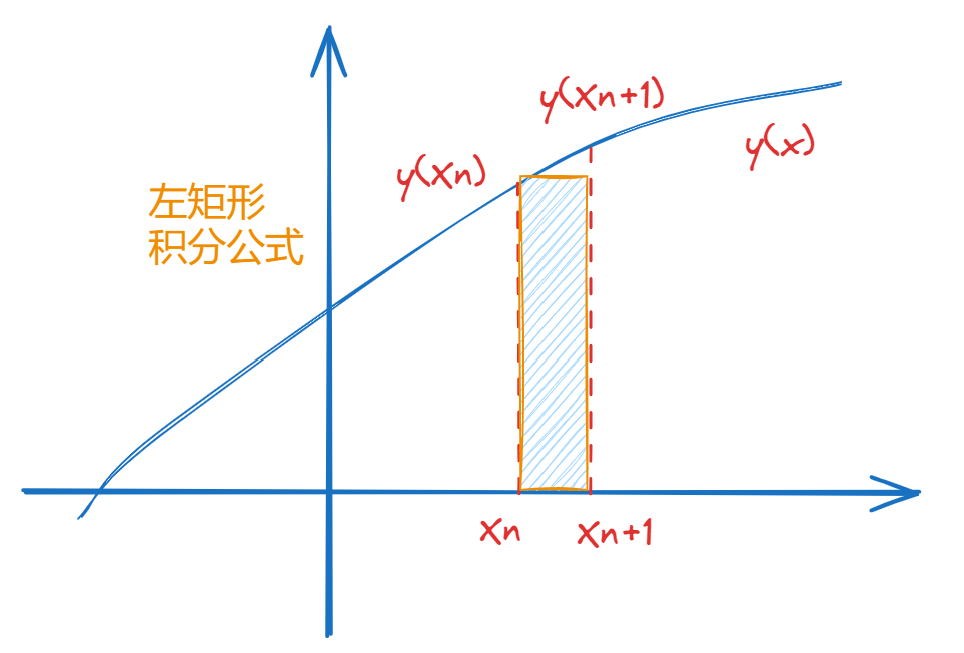
则可以得到欧拉公式:
3.1 后退欧拉公式
采用右矩形积分公式,有:
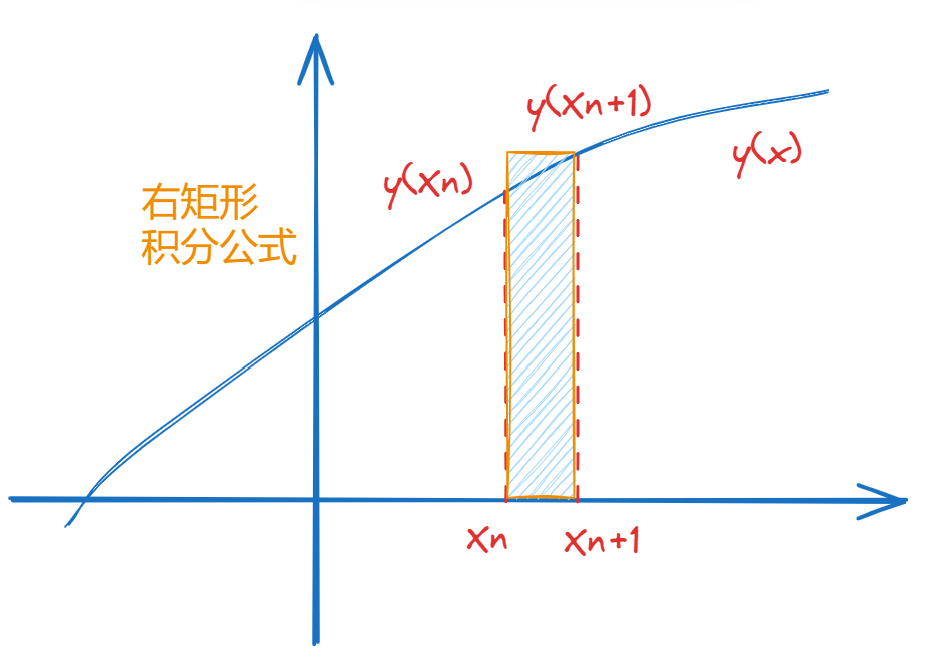
则可以得到后退欧拉公式:
3.2 改进欧拉方法-梯形积分
采用梯形积分公式计算公式(3),有:

代入公式(2),则有:
梯形求积公式比矩形求积公式的代数精度高,因此改进欧拉方法-梯形积分比公式(1.1)精度更高

- 使用梯形公式计算例题9.1.2
...
# 使用梯形公式计算
def TrapeEuler(f,y0,a,b,n,tol:float=1e-10):
"""梯形欧拉公式求解常微分方程"""
h=(b-a)/n
xi=[a+i*h for i in range(n+1)]
yi=np.zeros(n+1)
yi[0]=y0
for i in range(1,n+1):
# 循环迭代
yt0=yi[i-1]
while True:
# 计算t+1的y_{n+1}近似值
yt_next=yi[i-1]+0.5*h*f(xi[i-1],yt0)+0.5*h*f(xi[i],yt0)
# 计算误差
err=abs(yt_next-yt0)
if err<tol:
yi[i]=yt_next
break
else:
yt0=yt_next
return xi,yi
...
ns=[10,50,100,200]
xi20,yi20=TrapeEuler(f,y0,a,b,ns[0])
plt.plot(xi20,yi20,label=f'Trapezoidal Euler Method-h={(b-a)/(ns[0])}',marker='*')
xi21,yi21=TrapeEuler(f,y0,a,b,ns[1])
plt.plot(xi21,yi21,label=f'Trapezoidal Euler Method-h={(b-a)/(ns[1])}',marker='*')
xi22,yi22=TrapeEuler(f,y0,a,b,ns[2])
plt.plot(xi22,yi22,label=f'Trapezoidal Euler Method-h={(b-a)/(ns[2])}',marker='*')
xi23,yi23=TrapeEuler(f,y0,a,b,ns[3])
plt.plot(xi23,yi23,label=f'Trapezoidal Euler Method-h={(b-a)/(ns[3])}',marker='*')
....
plt.plot(xi20,[abs(yi20[i]-y(xi20[i])) for i in range(len(yi20))],label=f'trapezoidal-Improve Euler Method-h={(b-a)/ns[0]}')
plt.plot(xi21,[abs(yi21[i]-y(xi21[i])) for i in range(len(yi21))],label=f'trapezoidal-Improve Euler Method-h={(b-a)/ns[1]}')
plt.plot(xi22,[abs(yi22[i]-y(xi22[i])) for i in range(len(yi22))],label=f'trapezoidal-Improve Euler Method-h={(b-a)/ns[2]}')
plt.plot(xi23,[abs(yi23[i]-y(xi23[i])) for i in range(len(yi23))],label=f'trapezoidal-Improve Euler Method-h={(b-a)/ns[3]}')
...
不同的步长h对数值解的影响:
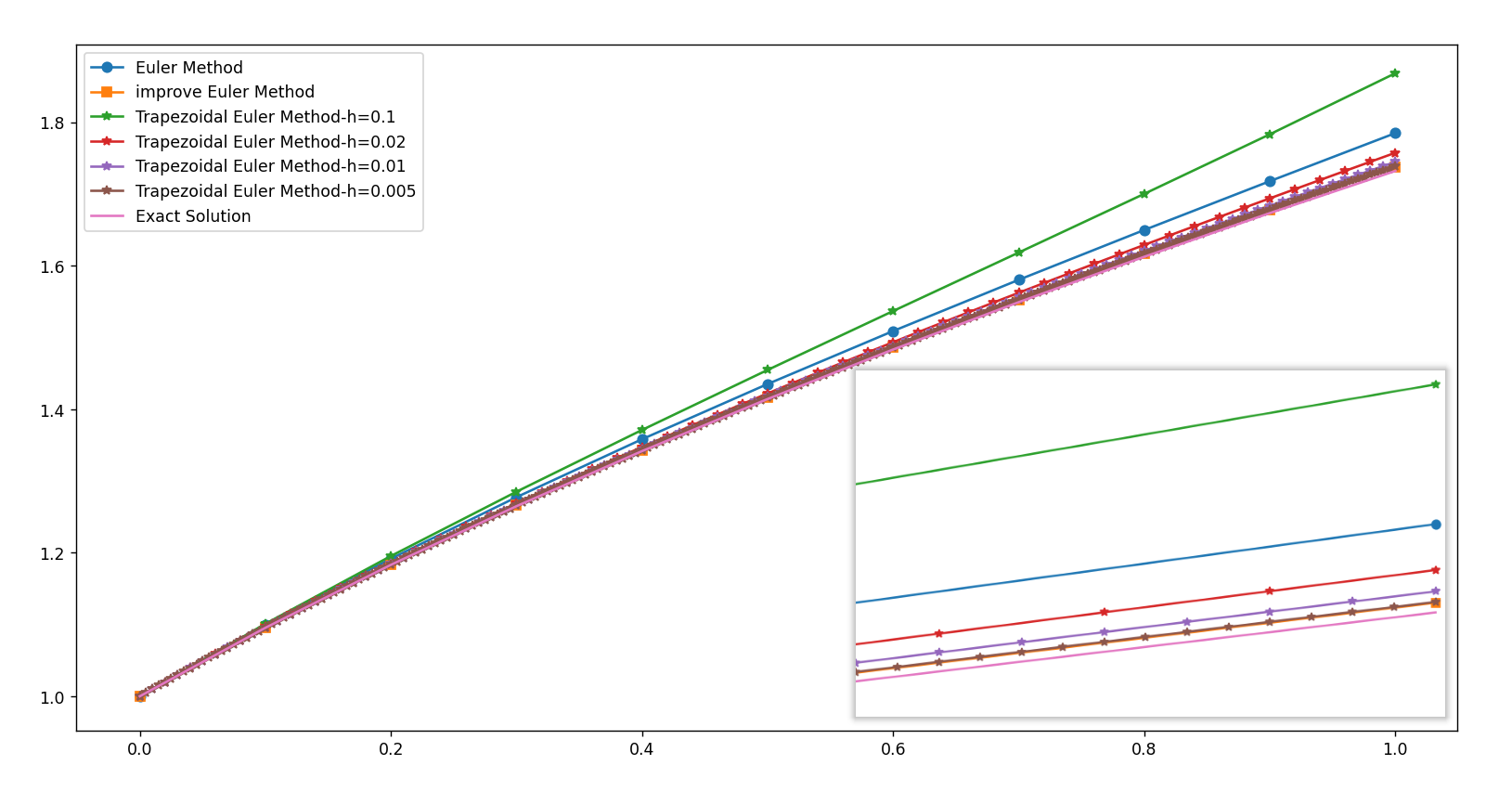
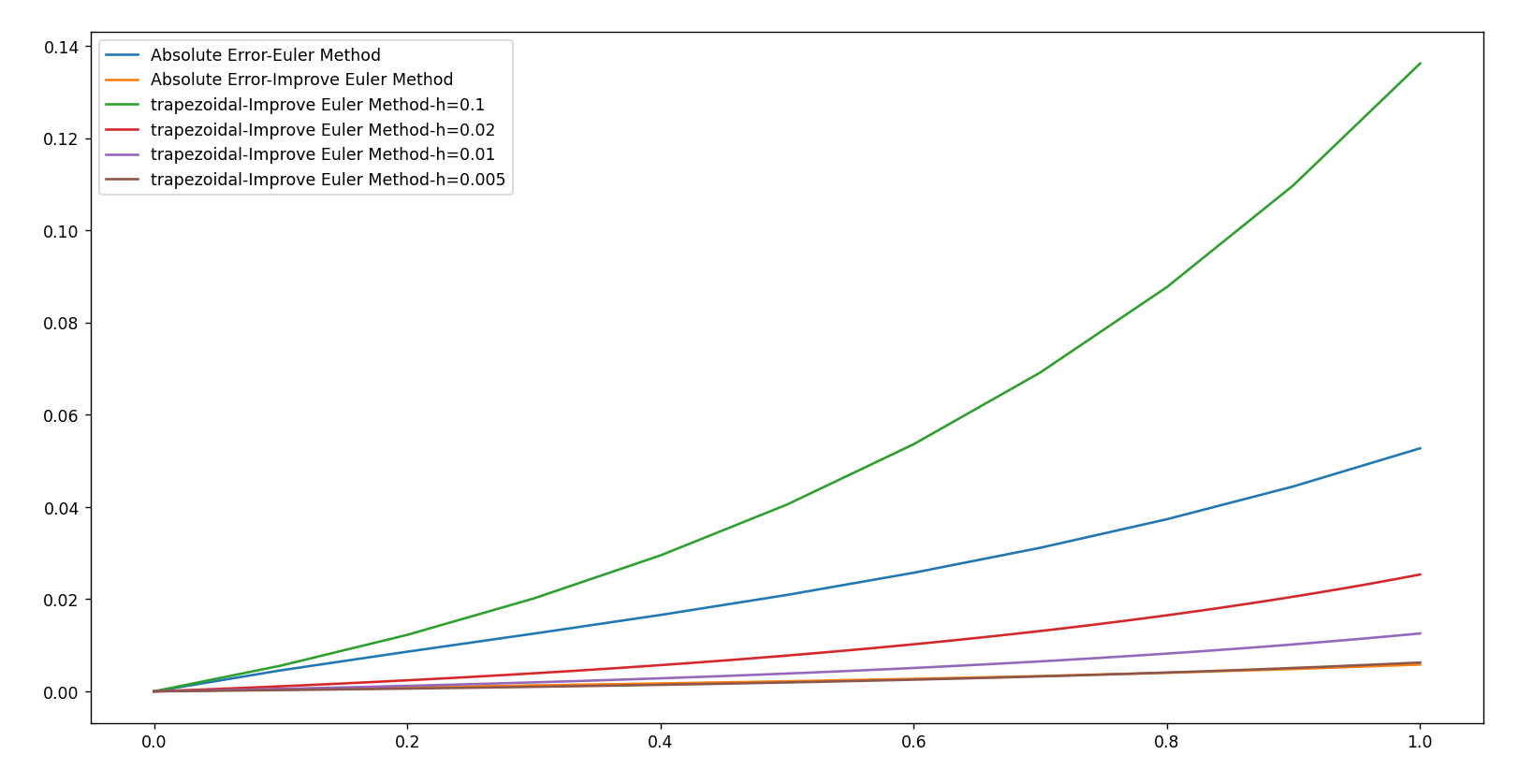
不同步长h对数值解的误差:h->0时,误差趋于0.可以发现梯形公式的误差最后趋向于改进欧拉公式的误差
3.3 利用高阶数值积分的离散格式
- 亚当斯 – 巴什福思 (Adams-Bashforth) 公式
- 亚当斯 – 莫尔顿 (Adams-Moulton) 公式
欧拉公式与梯形公式只需\(y_n\)就可以计算\(y_{n+1}\),称为单步法
亚当斯 – 巴什福思公式与亚当斯 – 莫尔顿公式计算 \(y_{n+1}\) 时 , 除了要知道 \(y_n\) 外 , 还需知道 \(y_{n−1} , y_{n−2}\) 等 , 这类公式称为多步法
对于欧拉公式和亚当斯 – 巴什福思公式这类,右端不含有\(y_{n+1}\)的方法,称为显式格式
对于梯形公式与亚当斯 – 莫尔顿公式的右端隐含 \(y_n+1\),计算\(y_{n+1}\)需要求解非线性方程的方法,称为隐式格式
3.4 局部截断误差
局部截断误差可用于表征求解初值问题的数值方法的计算精度.
一般地 , 常微分方程初值问题的数值解满足形如:
的等式 , 其中\(y_{n},\cdots,y_{n-r}\text{ 为 }y\text{ 在 }r+1\text{ 个节点 }x_{n},\cdots,x_{n-r}\text{ 处的数值解}.\)
数值方法的局部截断误差为:
真解与近似解之间的差异 \(\varepsilon_n = y(x_n ) − y_n\) 称为数值方法的整体截断误差

3.5 预估校正格式(改进欧拉算法)
梯形方法公式(4)比欧拉公式(1.1)精度得到提升,但计算量大增.一种有效简化计算的方法是:当h较小时,先使用显式格式计算合适的预估值\(\bar{y_{n+1}}\),
后利用隐式格式迭代一二次计算校正值\(y_{n+1}\).称为预估校正方法
- 一阶预估二阶校正公式
其中一种预估校正公式是:
通常称为改进的欧拉公式,另一种表示为:

改进欧拉方法精度高于欧拉公式,但小于梯形公式.计算量远小于梯形公式.
一般地 , 较为简单的预估校正格式都包含两个计算公式 , 一个是显式公式 , 作为预估公式 ; 另一个是隐式公式 , 作为校正公式 , 当然也可以构造包含多个计算公式的预估校正格式
构造预估校正格式时 , 应该注意阶数的匹配, 例如在式 (5) 中 , 校正公式具有二阶精度 , 而预估公式仅具有一阶精度 . 因为提供的预估精度较差 , 且仅经一次校正 , 校正值的精度不会太高
3.5.1 python 代码实现
- 使用改进欧拉公式计算例题9.1.2
# -*- coding: utf-8 -*-
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
def f(x,y)->float:
return y-2*x/y
y0,a,b,n=1,0,1,10
def y(x)->float:
return np.sqrt(1+2*x)
xi,yi=EulerMethod(f,y0,a,b,n)
plt.plot(xi,yi,label='Euler Method')
xi1,yi1=ImproveEulerMethod(f,y0,a,b,n)
plt.plot(xi1,yi1,label='improve Euler Method')
plt.plot(xi,[y(i) for i in xi],label='Exact Solution')
plt.legend()
plt.show()
plt.plot(xi,[abs(yi[i]-y(xi[i])) for i in range(len(yi))],label='Absolute Error-Euler Method')
plt.plot(xi1,[abs(yi1[i]-y(xi1[i])) for i in range(len(yi))],label='Absolute Error-Improve Euler Method')
plt.legend()
plt.show()
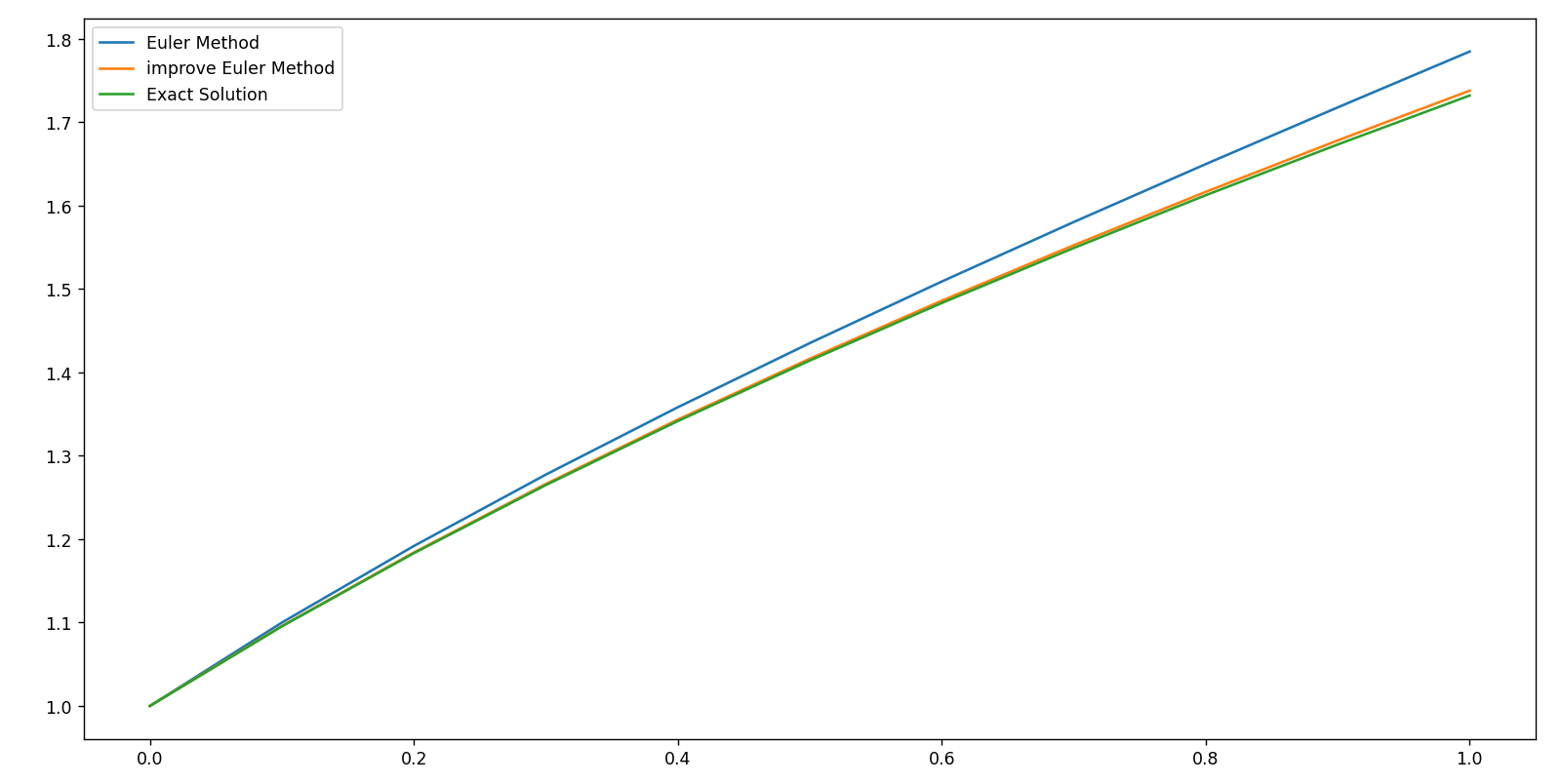
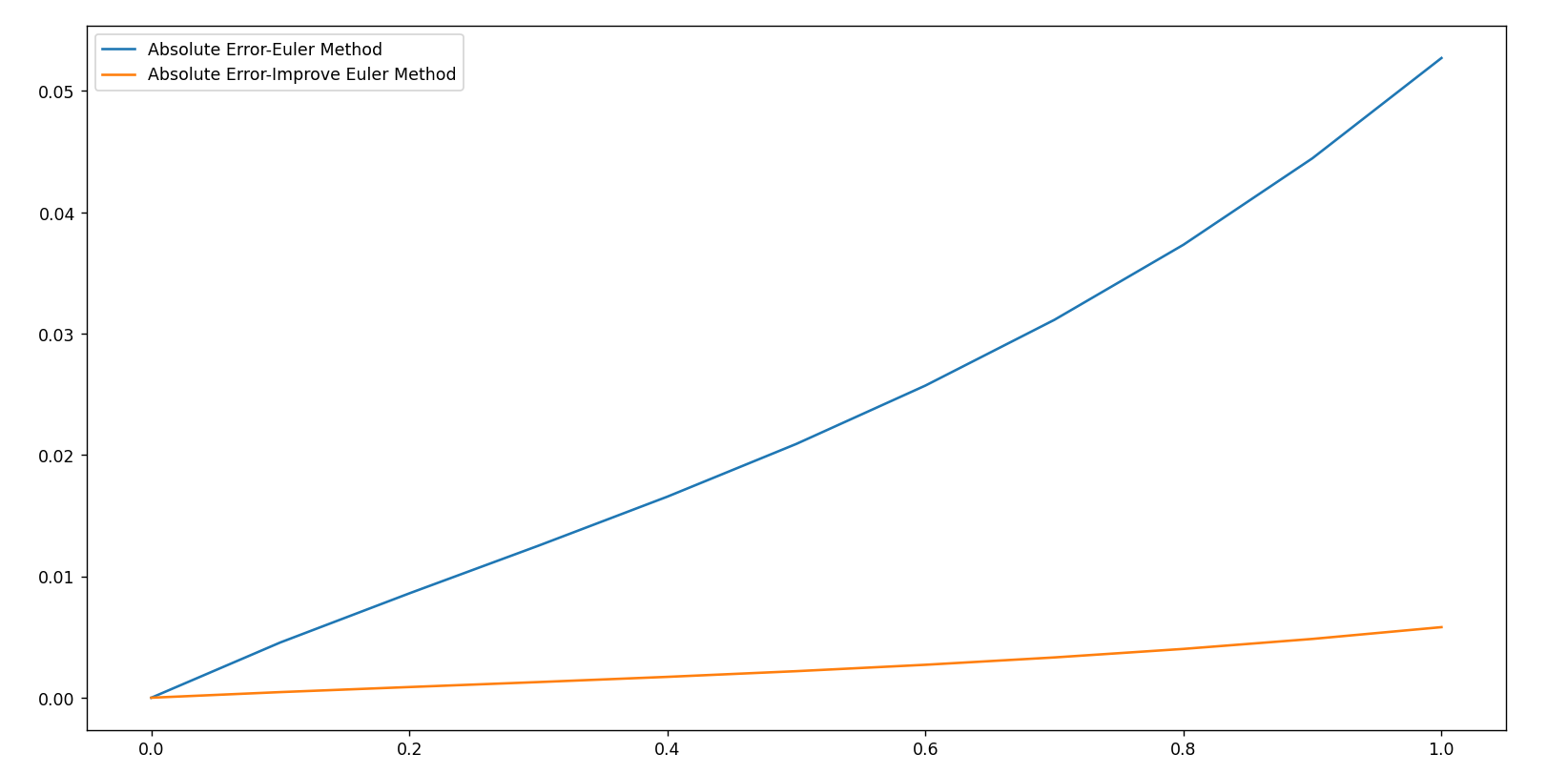
算法误差对比
- 二阶预估二阶校正格式
公式(6)的预估公式/校正公式都具有二阶精度 , 因此精度更高.
- 四阶亚当斯预估校正系统
公式(7)的预估公式/校正公式都具有四阶精度 , 因此精度更高.
4.龙格 – 库塔公式( R-K 方法)
这是一种广泛应用的高精度显式单步法.
龙格 – 库塔公式的基本思想就是设法计算 f(x,y) 在某些点上的函数值 , 然后对这些函数值作线性组合 , 构造近似计算公式 , 再把近似公式和解的泰勒展开式相比较 , 使前面的若干项吻合 , 从而获得达到一定精度的数值计算公式 .
一般的显式龙格 – 库塔公式的形式为:
其中 \(\omega_i\), \(\alpha_i\) 和 \(\beta_{ij}\) 是参数,与公式(1)右端得到f(x,y)及步长h无关. 上式成为r段的龙格 – 库塔公式.特别地 , 若式 (8) 与 \(y(x_{n+1} )\) 的泰勒展开式的前 p + 1项完全一致 , 即局部截断误差达到 \(O(h^{p+1} )\), 则称公式 (8) 为 p阶r段龙格–库塔公式
龙格 – 库塔公式是一类公式 , 每确定一组特殊的系数 , 就得到一个特殊的龙格 – 库塔公式
<<现代数值计算 第二版>>p226页给出了一个二阶二段的龙格 – 库塔公式推导过程,这里不再赘述.
4.1常用的R-K公式
4.1.1二阶二段龙格 – 库塔公式(R-K22)
这就是前面的预估校正公式
该格式称为中点公式 .
4.1.2 三阶三段龙格 – 库塔公式(R-K33)
4.1.3 三阶三段 Heun 公式
4.1.4 标准四阶四段龙格 – 库塔公式
在实际应用中 , 最常用的是标准四阶四段龙格 – 库塔公式 .
4.1.5 四阶四段 Gill 公式
RK方法的阶数与计算函数值的次数之间的关系并非等量增加的 ,事实上 , 对于大量的实际问题 , 四阶的龙格 – 库塔公式已可满足对精度的要求 :


- RK44计算例题9.1.2
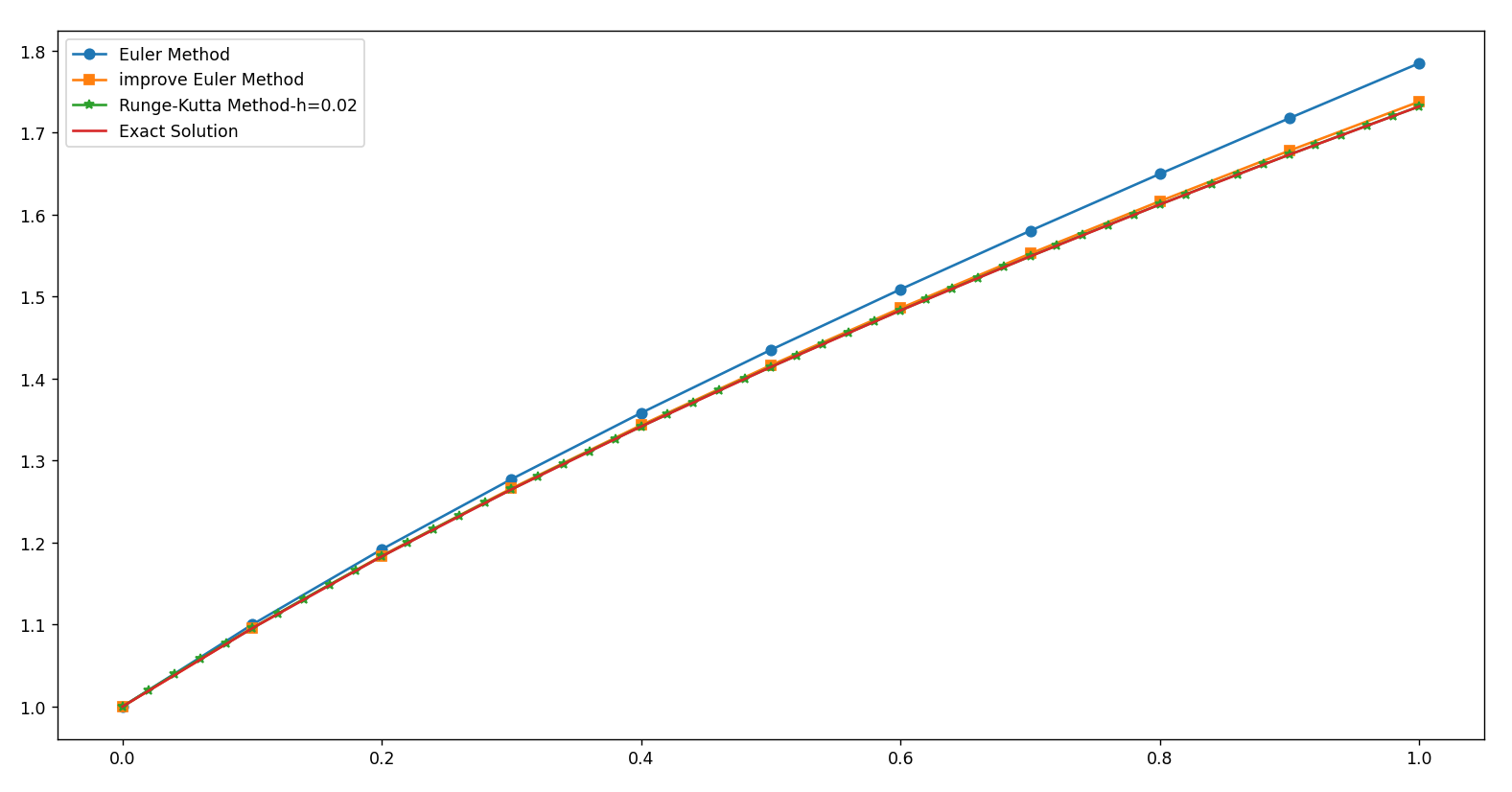

4.2龙格 – 库塔公式的优缺点
- 在求解范围较大而精度要求较高时是比较好的方法
- 显示格式且自启动.
- R-K公式基于泰勒展开,因此要求解函数y(x)具有较好的光滑性质
- 如果解y(x)光滑性差 , 那么四阶龙格 – 库塔公式求得的数值解精度可能反而不如改进的欧拉公式
5. 收敛性与稳定性


6. 微分方程组和刚性问题
本节讨论常微分方程组的数值解法
6.1 一阶常微分方程组
前面在未知函数个数 m = 1情况下得到的大部分结论都可平行地推广到 m > 1 的情况 ;前文介绍的梯形公式、预估校正格式和龙格 – 库塔公式均可应用于一阶常微分
方程组的求解 . 只是在进行理论分析时 , 需要将绝对值替换为向量范数
例如,考虑以下方程组:
将区间 [0,10] 进行 N 等分 , 记 \(h =10/N\).将欧拉公式 (1.1) 应用于该问题 , 则有:
判断欧拉方法求解的绝对稳定性.可知方程组扰动表达式为:
矩阵\(\left(\begin{array}{cc}0&1\\-x^2&-x\end{array}\right)\)的特征值为\(\lambda_{1,2}=\mathrm e^{\pm\frac{2\pi}{3}\mathrm i}x\). 可以证明当\(|h\lambda_i|<1(\text{或 }h<0.1)\)时,有:
即该方法是绝对稳定的
6.2 高阶常微分方程初值问题
记:
则可将高阶微分方程化为一阶微分方程组:
例如,考虑初值问题:
令\(y=u,y^{\prime}=v,\)该初值问题转化成一阶常微分方程组:
6.3 刚性方程组

例如 , 考虑常微分方程组
这就是一个刚性方程组 , 其雅可比矩阵为\(\left(\begin{array}{cc}9&24\\-24&-51\end{array}\right),\)刚性比\(s={\frac{|-39|}{|-3|}}=13\),存在唯一解:
求解刚性问题的困难之处:为保证算法的稳定性 , 必须将步长限制在较小的范围内.若需要计算到某一个较长的区间 , 则需要迭代非常多的时间步 . 这导致计算量大 , 并且由于舍入误差的累计 , 结果也很不准确

对于刚性问题 , 如果扩大数值方法的绝对稳定区域,步长的限制讲大大减少.若某数值方法是 A- 稳定的 , 则应用该方法时步长可随意选取 , 不再受稳定性限制
显式多步法和显式龙格 – 库塔法不可能是 A- 稳定的 , A- 稳定的隐式线性多步法的阶不超过 2, 而梯形公式是二阶隐式线性多步法中精度最高的一个
实际计算时 , 常采用隐式或半隐式的龙格 – 库塔公式求解刚性方程组
以下是 A- 稳定的的常用计算格式:
一段二阶隐式龙格 – 库塔方法
二段二阶隐式龙格 – 库塔方法
二段四阶隐式龙格 – 库塔方法
半隐式龙格 – 库塔方法
7. 有限差分法
简单介绍该方法的基本思想
有限差分法离散微分方程包含两步:
- 第一步是将求解区域进行网格剖分 ;
- 第二步是将微分方程在节点处进行离散化 .
建立差分格式的离散化方法有多种 , 这里仅介绍以差商代替微商的方法
以第二类常微分问题(两阶常微分方程边值问题为例子):
对于内部节点 \(x_n (n = 1,2,··· ,N − 1)\), 由泰勒展开公式得
\([ ]_n\) 表示方括号内的函数在点 \(x_n\) 取值,所以方程(16)在\(x_n\)写成:
h 充分小时 , \(R_n (y)\) 是的二阶无穷小量,因此差分方程为,\(R_n (y)\) 为截断误差:
对于边界节点 , 由边界条件知 \(y_{0}=\alpha, y_{N}=\beta.\)
可得到关于 y_n 的线性代数方程组:
记方程组的未知向量\(y_h = (y_1,y_2,\cdots,y_{N-1})^\mathrm{T},\) 右端向量为\(g = \left(f_{1} + \frac{\alpha}{h^{2}},f_{2},\cdots,f_{N-1} +\frac{\beta}{h^2}\right)\),系数矩阵为:
则有:
易知 , H 为对称正定矩阵 , 故该方程组有唯一解 . 此外 , 由于矩阵 H 为三对角阵

本文来自博客园,作者:FE-有限元鹰,转载请注明原文链接:https://www.cnblogs.com/aksoam/p/18358486

 常微分方程初边值问题数值解
常微分方程初边值问题数值解

