【数值计算方法】非线性方程求根
第七章 非线性方程求根
思维导图
非线性方程求根
非线性方程求根的基本问题
非线性方程求解的问题也可以提为:\(f(x)=y\),其中:\(f : \mathbb{R}^n \to \mathbb{R}^m\) 是一个非线性函数,\(y\in\mathbb{R}^m\) 是给定的向量,\(x\in\mathbb{R}^n\) 是一个未知向量.
一般的,令\(g(x)=f(x)-y\),原问题等价于\(g(x)=0\)


1. 二分法
设有单变量连续函数 f(x), 若存在某一连续区间 [a,b] 使得 \(f(a)f(b) < 0\), 即函数值异号 ,则 f 在区间 [a,b] 中至少存在一个零点
二分法的基本思想就是每次把区间二等分 , 给出两个等分区间中有根的那个区间 , 达到把区间缩小的目的 . 二分法的具体做法如下:
记\(a_1=a,b_1=b\), 令\(x_1 = (a_1 + b_1 )/2\),考虑下面各种情形.若 \(f(x_1 ) = 0\), 则 \(x_1\) 是函数 \(f\) 的一个零点.否则\(f(x_1)\)必定与\(f(a_1)f(b_1)\)异号, 则有\(f(a_1)f(x_1) < 0\)或者\(f(x_1)f(b_1) < 0\);
下一步\(a_2 = a_1, b_2 = x_1\), 否则\(a_2 = x_1, b_2 = b_1\). 重复以上过程, 直到 \(f(x_n)\) 与 \(f(x_{n-1})\) 符号相同, 则 \(x_n\) 是函数 \(f\) 的一个零点.
每个区间有如下的几个性质:
- \(f(a_k)f(b_k)<0\),至少存在一个根\(x^{*}\),对于所有的\(k,x^{*} \in [a_k,b_k]\);
- \(b_k - a_k=(b-a)/2^{k-1}\), 其中\(k=1,2,3,\cdots\);
- \(x_k=(a_k+b_k)/2\),并且,\(|x_k-x^{*}|<\frac{b-a}{2^{k}}\);
二分法是线性收敛的,对于指定精度\(\epsilon\),最多需要迭代步数:
$\lceil x\rceil $表示向上取整
- 二分法算法描述

- 优缺点
二分法对函数的要求低 , 仅需要函数的连续性 , 编程简单;但是二分法只用到了函数值的符号 , 而非函数值的大小 , 因此收敛速度并不快 . 另一方面 , 二分法不能求复根 , 一般不能求偶数重根 , 也不能直接应用到多变量的情形
算法实现
def BSMethod(f,a,b,tol=1e-5)->float:
"""二分法求解非线性方程f(x)在区间[a,b]的根
input:
f: callable, 单变量非线性方程
a: float, 区间左端点
b: float, 区间右端点
tol: float, 误差限/精度
output:
x: float, 方程f(x)的根
"""
a0,b0=a,b
maxIter=np.ceil(np.log2(np.abs(b-a)/tol))
if f(a)*f(b)>0:
raise ValueError("方程f(x)在区间[a,b]上无根")
i=0
while True:
if i>=maxIter:
raise ValueError("迭代次数过多")
c=0.5*a0+0.5*b0
if np.abs(b0-a0)<tol or np.abs(f(c))<=tol:
return c
if np.sign(f(a0))*np.sign(f(c))>0:
a0=c
i+=1
else:
b0=c
i+=1
- 例题
# 求方程$f(x)=x^3-x-1$在区间[1,2]的根.
from formu_lib import *
import numpy as np
f=lambda x:x*x*x-x-1
BSMethod(f,1,2,1e-4)
- 输出:
1.32470703125
借鉴数值积分中的复合中点,梯形,辛普森积分公式,可以得到复合-二分法求根公式,python实现如下:
算法实现
def ComBSMethod(f,a,b,n:int=200,tol=1e-5)->list[float]:
"""将区间[a,b]按照步长sep分成n个子区间[a,a+i*h]....[b=sep,b],判断区间端点是否异号,
用二分法求解方程f(x)的根"""
h=np.abs(b-a)/n
xis=[(a+i*h,a+(i+1)*h) for i in range(n)]
results=[]
for xi in xis:
# 遍历每个子区间
x_1,x_2=xi[0],xi[1]
if np.sign(f(x_1))*np.sign(f(x_2))<0:
# 如果异号,则用二分法求解方程f(x)的根
x,flag=BSMethod(f,x_1,x_2,tol=tol)
if flag:
results.append(x)
return results
- 例题
例题代码
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
# 计算f(x)=x*sin(x)/(x*x+1)的根
f=lambda x:x*np.sin(x)/(x*x+1)
xs=np.linspace(-10,10,1000)
fs=[f(x) for x in xs]
plt.plot(xs,fs,label='f(x)')
plt.plot([-10,10],[0,0],label='zero-line')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
roots=ComBSMethod(f,-10,10,500,1e-6)
if len(roots)>0:
plt.scatter(roots,[f(x) for x in roots],label='roots',marker='o')
plt.show()
for root in roots:
print(f"root={root:.6f},f(root)={f(root):.6f}")
# root=-9.424785,f(root)=-0.000001
# root=-6.283184,f(root)=-0.000000
# root=-3.141592,f(root)=0.000000
# root=3.141592,f(root)=0.000000
# root=6.283184,f(root)=-0.000000
# root=9.424785,f(root)=-0.000001

2. 不动点迭代法
参考:线性方程组\(Ax=b\),等价于\(x=Bx+g\),从而有迭代格式\(x^{k+1}=Bx^k+g\).非线性方程\(f(x)=0\),也可以写成\(x=\phi(x)\),从而有迭代算法\(x_{k+1}=\phi(x_k)\),不同的是, 这种产生函数\(\phi\)的方式可以有很多种 , 甚至可以说是无穷无尽的.
若把函数 ϕ 看成是一个映射 , 求解 \(x^∗\) 满足 \(f(x^∗) = 0\) 相当于求解 \(x^∗ = ϕ(x^∗)\), 即求在映射 ϕ下不动的点 . 因此 ,方程 \(x = ϕ(x)\) 称为不动点方程 , \(x^∗\) 称为函数 ϕ 的不动点 , 该问题也称为不动点问题
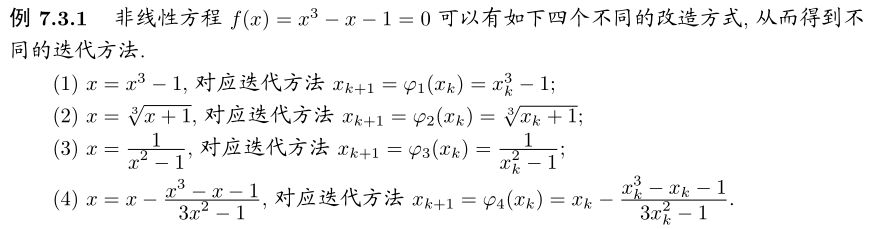
但是,不同的的不动点函数\(\phi\)收敛性不尽相同,收敛速度也不同,上面四种迭代格式中第一种,第三种都会发散..
2.1 什么样的不动点函数\(\phi(x)\)才会收敛?

根据以上定理,可知当:
时,迭代格式\(x_{k+1}=\phi(x_k)\)产生的序列\({x_k}\)收敛于\(x^∗\),且\(x^∗\)是唯一的.
收敛速度的估计可知 , 当 L 较小时 , 收敛较快 , 反之 , 当 L 很靠近 1 时收敛很慢 . 若L > 1, 则迭代不收敛
2.2 例题

- 迭代函数推到和验证
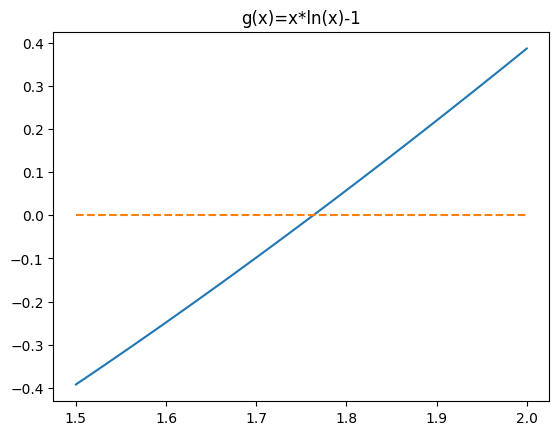
\(1.5\ln1.5-1=-0.391 8<0, 2\ln2-1=\ln4-1>0,\) 因此原方程在区间 [1.5,2] 中有一根 . 记四个迭代函数分别为\(\phi_{1}, \phi_{2}, \phi_{3}, \phi_{4}.\),对迭代函数求导:
计算导数在[1.5,2]的极大值:
有定理7.3.2可知,\(\phi_1\)不满足\([0,1)\).
例题四种迭代函数的Python代码和输出
- python 代码
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
def f1(x):
return 1/np.log(x)
def f2(x):
return np.exp(-x)
def f3(x):
return x-(x*np.log(x)-1)/3.0
def f4(x):
return (x+1)/(np.log(x)+1)
# 绘制原函数
x=np.linspace(1.5,2,50)
plt.plot(x,[xi*np.log(xi)-1 for xi in x])
plt.plot([1.5,2],[0,0],label='0-line',linestyle='--')
plt.title('g(x)=x*ln(x)-1')
plt.show()
plt.plot(x,f1(x),label='f1(x)')
plt.plot(x,f2(x),label='f2(x)')
plt.plot(x,f3(x),label='f3(x)')
plt.plot(x,f4(x),label='f4(x)')
plt.plot([1.5,2],[1.5,1.5],label='low-line',linestyle='--')
plt.plot([1.5,2],[2,2],label='up-line',linestyle='--')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.title('f1(x)=1/ln(x),f2(x)=e^{-x},f3(x)=x-(x*ln(x)-1)/3,f4(x)=(x+1)/(ln(x)+1)')
plt.show()
# 不动点迭代法
maxiter=100
a,b=1.5,2
x0=1.7
x1,x2,x3,x4=[],[],[],[]
for i in range(maxiter):
x1.append(x0)
x_next=f1(x0)
if x_next<0:
break
if np.abs(f1(x_next))<1e-6:
break
else:
x0=x_next
x0=1.7
for i in range(maxiter):
x2.append(x0)
x_next=f2(x0)
if np.abs(f2(x_next))<1e-6:
break
else:
x0=x_next
x0=1.7
for i in range(maxiter):
x3.append(x0)
x_next=f3(x0)
if x_next<0:
break
if np.abs(f3(x_next))<1e-6:
break
else:
x0=x_next
x0=1.7
for i in range(maxiter):
x4.append(x0)
x_next=f4(x0)
if x_next<0:
break
if np.abs(f4(x_next))<1e-6:
break
else:
x0=x_next
plotLines([list(range(len(x1))),list(range(len(x2))),list(range(len(x3))),list(range(len(x4)))],
[x1,x2,x3,x4],['f1(x)','f2(x)','f3(x)','f4(x)'],
title='Four forms of fixed point iteration errors',oneY=True)
- 函数\(f(x)=x*ln(x)-1\)在[1.5,2]区间的函数图像
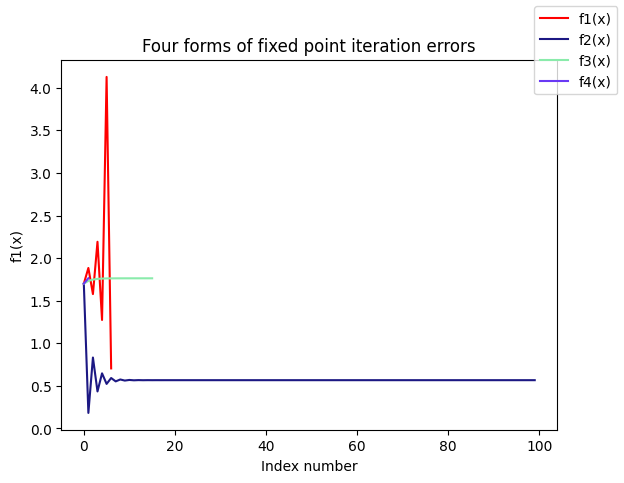
- 四个不动点函数在[1.5,2]的取值范围,定理7.3.2第一的条件

- 四个不动点函数的迭代过程:可以发现只有第三,第四个迭代函数收敛
2.3 迭代加速
假设有不动点迭代 \(x_{k+1} = \varphi(x_k )\), 且设不动点为 \(x^∗\) . 在前面不动点迭代的收敛分析中,有:
其中\(\xi_k\)是任意的不动点迭代点,且\(\varphi'(\xi_k)>0\).
如果\(\varphi'(x_k)\)变化不大,那么可以认为\(\varphi'(x_k)=L\),则有:
上式可以理解为:两步迭代近似值的一种平均,或者看成另一个新的迭代方法,对应的不动点函数为:
上述假定下,\(\bar{\varphi}'(x_k)\)几乎为零,因此迭代速度很快,该公式有赖于\(\varphi(x)\)导数估计的准确性.
- 例题

例题代码
- python 代码
# 使用迭代加速,加速收敛
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
def f3new(x):
L=0.48335
return (x-(x*np.log(x))/3.0+1/3.0-L*x)/(1-L)
maxiter=100
a,b=1.5,2
x0=1.7
x3new=[]
for i in range(maxiter):
x3new.append(x0)
x_next=f3new(x0)
if x_next<0:
break
if np.abs(f(x_next))<1e-6:
break
else:
x0=x_next
plt.plot(list(range(len(x3new))),x3new,label=f'x3 new iter acceleration-num:{len(x3new)}')
plt.plot(list(range(len(x3))),x3,label=f'origin x3 iter acceleration-num:{len(x3)}')
plt.xlabel('iteration')
plt.ylabel('root')
plt.legend()
plt.title('iter acceleration VS origin iter')
plt.show()
- 对比加速前的\(\phi_3(x)\)和\(\bar{\phi_3}(x)\)的收敛性

2.4 艾特肯 (Aitken) 加速方法
当\(\varphi'(x)\)变化不大,这种加速方法可以在不估计导数情形下加速迭代
根据前面的方法 , 有:
因为\(\varphi'(x)\)变化不大,所以\(\varphi'(\xi_{k})\approx\varphi'(\xi_{k-1})\),可解得:
根据上式,原本迭代序列为\({x_k}\),可以根据公式(3)得到新的迭代序列\({\bar{x}_k}\),一般的,后者的收敛速度快得多,特别是线性收敛的序列
aitken加速方法避开了导数估计,但缺陷是当\(x_{k-1},x_k,x_{k+1}\)都很靠近\(x^*\)时,公式(3)中分子分母就会接近0.当这时,可以用双精度计算
另一种aitken 加速公式:

- 例题
对例 7.3.3 中的迭代函数 \(φ_3 (x)\) 做艾特肯加速
- python 代码
例题代码
# 使用aitken加速,加速收敛
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
a,b,x0,maxiter=1.5,2,1.7,100
x3aitken=[]
while True:
x3aitken.append(x0)
# aikten加速公式
x_next=x0-((f3(x0)-x0)**2)/(f3(f3(x0))-2*f3(x0)+x0)
if x_next<0:
break
if np.abs(f(x_next))<1e-15:
break
else:
x0=x_next
if len(x3aitken)>maxiter:
break
# plt.plot(list(range(len(x3new))),x3new,label=f'x3 new iter acceleration-num:{len(x3new)}')
plt.plot(list(range(len(x3aitken))),x3aitken,label=f'x3 aitken iter acceleration-num:{len(x3new)}')
plt.plot(list(range(len(x3))),x3,label=f'origin x3 iter acceleration-num:{len(x3)}')
plt.xlabel('iteration')
plt.ylabel('root')
plt.legend()
plt.title('iter acceleration VS origin iter-tol:1e-15')
plt.show()

3. 牛顿法
牛顿法是求解非线性方程的一个重要方法 , 有时也称为牛顿 – 拉弗森 (Newton-Raphson)方法
对于非线性方程\(f(x)=0\),f(x)二阶连续可微函数,\(x_k\)是f(x)的近似解.f(x)在\(x_k\)处泰勒展开:
取泰勒展开的前两项 , 称函数 h 是函数 f 的线性化:
求解\(h(x)=0\),把它的根作为 f 的更好的近似根 , 则有:
这相当于不动点迭代法的一种特例 \(\varphi(x)=x-\frac{f(x)}{f^{'}(x)}\), 称为牛顿法.
牛顿法的几何意义:通过计算切线,不断逼近零点.

如果将牛顿法视为特殊的迭代加速法:
方程\(f(x)=0\)等价于\(x=x+f(x)=\phi(x)\),这是不动点迭代的一种形式,令\(L=\phi'(x_k)=1+f'(x)\),则有:
这是牛顿法的迭代公式.
- 牛顿法的局部收敛性 , 我们有如下的定理 :

- 牛顿法有下面的全局收敛性理论 :

上面的定理实际上要求初始点要有一定的性质 , 下面的定理仅需要初始点落在某一区间内

对于f(x)=0有重根的情况,牛顿法一般无法二阶收敛,, 牛顿法的全局收敛性不管是对函数还是对初始点 , 要求都是比较高的,而牛顿下山法可以有效降低这些要求
3.1 牛顿下山法
- 基本思想
在一定的条件下 , 求解方程 f(x) = 0 等价于求函数 |f(x)| 的最小点. . 若把函数|f(x)| 的图像想象为许多山峰的话 , 求极小点就相当于找到山谷谷底.牛顿法如果不收敛 , 通常是在两面 ( 或更多 ) 山坡之间跳跃 , 每次都跳过谷底 . 从函数的角度来讲 , 这个现象出现是因为每次修正迭代点 \(x_k\) 时 , 修正的幅度太大了
- 迭代公式
牛顿下山法的迭代公式为:
牛顿法对应的参数 λ 恒为 1, 而下山法的参数 λ 是每一步变化的 , λ 取满足函数值下降条件 \(|f(x_{k+1} )| < |f(x_k )|\) 的 1,0.5,0.25...中最大的那个值

牛顿下山法对初始点没有特别的要求 , 因此整个算法对初始点的依赖大大减小 , 原来用牛顿法不收敛的问题用下山法就可能收敛了 . 下山法是一种技巧 .
4. 割线法
牛顿法是二阶收敛的 , 但是要算导数 , 多变量情形时会有很大的计算量 . 割线法使用近似计算的方法代替牛顿法中的导数, 使算法较快收敛 , 同时计算量较小且不需要计算导数 . 下面考虑单变量f(x)=0的情形.
4.1 双点割线法
对于方程:
已有近似值$ x_{k−1} 和 x_k$ ,过点\((x_{k-1},f(x_{k-1}))\)和\((x_k,f(x_k))\)做一条直线,方程为:
则可以计算出该直线和x轴的交点\(x_{k+1}\):
再用 \(x_k , x_{k+1}\) 两点做同样的事情 , 进行迭代 , 此即为割线法 .

4.2 单点割线法
割线法每一个计算步骤都牵涉到前面两个点 , 如果没有两个初始值 , 则割线法无法开始计算 . 这时 , 若固定其中一个点 , 例如:
- 收敛性定理

4.3 牛顿法的python算法实现
code
def NewtonMethod(f,a:float,b:float,
tol:float=1e-5,
**kwargs)->float:
"""牛顿法求解非线性方程f(x)在区间[a,b]的根"""
if 'MAXITER' in kwargs.keys():
MAXITER=kwargs['MAXITER']
else:
MAXITER=2000
# 取左区间为起始点
x0,k=a,0
delta=(b-a)/100
df0=(f(x0+delta)-f(x0))/delta
while True:
x_next=x0-f(x0)/df0
if np.abs(f(x_next))<tol:
# 如果f(x)接近0,就停止迭代
return x_next
elif x_next<a or x_next>b:
# 如果x_next超出区间[a,b],就停止迭代
raise ValueError("方程f(x)在区间[a,b]上无根")
else:
x0=x_next
df0=(f(x0+delta)-f(x0))/delta
if k>MAXITER:
print(f"迭代次数{k},,不满足tol={tol}")
raise ValueError("迭代次数过多")
k+=1
def NewtonMethod_DownHill(f,a:float,df,
tol:float=1e-5,
**kwargs)->float:
"""牛顿下山法求解非线性方程f(x)在区间[a,b]的根
input:
f: callable, 单变量非线性方程
a: float, 区间左端点
df: callable, 导数函数
tol: float, 误差限/精度
delta: float, 差分步长
kwargs['df']: callable, 导数函数,如果未给定,那么就用前向差分公式f'(x)=[f(x+delta)-f(x)]/delta计算
output:
x: float, 方程f(x)=0的根
"""
import mpmath as mp
mp.dps=50
x0,k=mp.mpf(a),mp.mpf('0.0')
a=mp.mpf(a)
tol=mp.mpf(tol)
# 默认最大迭代数为2000
if 'MAXITER' in kwargs.keys():
MAXITER=kwargs['MAXITER']
else:
MAXITER=2000
results=[]
while True:
results.append(x0)
if mp.fabs(f(x0))<=tol:
return x0
d0=mp.mpf(-f(x0))/mp.mpf(df(x0))
lamda=mp.mpf('1.0')
while True:
x_next=x0+lamda*d0
if mp.fabs(f(x_next))<mp.fabs(f(x0)) :
break
else:
lamda=0.5*lamda
if lamda<mp.mpf('1e-20'):
break
# raise ValueError("line search failed")
x0=x_next
if k>MAXITER:
print(f"迭代次数{k},,不满足tol={tol}")
return x0
k+=1
def SecantMethod2Ps(f,a:float,b:float,
tol:float=1e-5,
**kwargs)->float:
"""2-点割线法求解非线性方程f(x)在区间[a,b]的根
input:
f: callable, 单变量非线性方程
a: float, 区间左端点
b: float, 区间右端点
tol: float, 误差限/精度
output:
x: float, 方程f(x)的根
"""
if 'MAXITER' in kwargs.keys():
MAXITER=kwargs['MAXITER']
else:
MAXITER=2000
x_0=a
x0=b
k=0
while True:
# print(f"x_0={x_0},x0={x0},f(x_0)={f(x_0)},f(x0)={f(x0)}")
x_next=x0-f(x0)*((x0-x_0)/(f(x0)-f(x_0)))
if np.abs(f(x_next))<=tol:
return x_next
elif x_next<a or x_next>b:
print(f"x_next={x_next},a={x_0},b={x0}")
raise ValueError("方程f(x)在区间[a,b]上无根")
else:
x_0=x0
x0=x_next
k+=1
if k>MAXITER:
print(f"迭代次数{k},,不满足tol={tol}")
非线性方程组求解
考虑如下的方程组:
其中,\(x=(x_1,x_2,\cdots,x_n)^\mathrm{T}\in\mathbb{R}^n\)是未知量;\(f_i\) 是定义在某区域 \(D\subset\mathbb{R}^{n}\) 上的 n 元实函数.若至少有一个 \(f_i\) 不是线性函数 , 则称上述方程组为非线性方程组
1.1 高斯 – 赛德尔迭代算法框架

步骤 (2) 中求解的是一个单变量的非线性方程, 可以用前面的各种方法求解.该问题求解不需要很精确 , 通常用牛顿法迭代一两步就可以
1.2 不动点方法算法框架
记向量函数 \(F(\boldsymbol{x})=(f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\cdots,f_n(\boldsymbol{x}))^\mathrm{T}:\mathbb{R}^n\to\mathbb{R}^n,\text{ 其中 }f_i(\boldsymbol{x})=f_i(x_1,x_2,\cdots,x_n)\) 是 x 的函数 ;若对于某个\(x\in\mathbb{R}^n,\text{ 存在 }x\text{ 的一个邻域 }\{\boldsymbol{z}| ||\boldsymbol{z}-\boldsymbol{x}|\leqslant\varepsilon,\varepsilon>0\}\subset D,\)则称 x 是 D 的内点.
对于 n 元向量函数 F, 若存在矩阵\(A(\boldsymbol{x})\in\mathbb{R}^{n\times n}\),使得:
则称 F 在 x 点处可微 , A(x) 称为函数 F 在 x 的雅可比矩阵 , 并与导数相类似 记 \(F' (x) =A(x)\).可以证明的是,, F 在 x 点可微的充分必要条件是每个分量函数 \(f_i (x)\) 关于每个变量 \(x_j\) 可微 :
若有函数 \(\boldsymbol{\Phi}(x):\mathbb{R}^n\to\mathbb{R}^n,\text{ 使得 }x=\boldsymbol{\Phi}(x)\text{ 等价于 }\boldsymbol{F}(x)=\boldsymbol{0},\)就可以构造向量函数的不动点迭代: \(x^{(k+1)}=\boldsymbol{\Phi}(\boldsymbol{x}^{(k)})\)


1.3 牛顿法算法框架
非线性函数\(F(x): \mathbb{R}^n\to\mathbb{R}^n\),在区域D中连续可微,分量函数为\(f_i(\boldsymbol{x})=f_i(x_1,x_2,\cdots,x_n),i=1,2,\cdots,n\),如果在某一迭代步有近似值\(\boldsymbol{x}^{(k)}=(x_1^{(k)},x_2^{(k)},\cdots,x_n^{(k)})^\mathrm{T}\in D,\),函数\(f_i(\boldsymbol{x})\)在\(\boldsymbol{x^{(k)}}\)点处泰勒展开,取线性部分:
向量形式为:
令上式左边为零 , 若\(F^{\prime}(x^{(k)})\)可逆 , 可从上式解出 x. 把求得的解作为新的迭代点 \(x^{(k+1)}\) :
此即为非线性方程组求根的牛顿法;计算导数矩阵\(F'(\boldsymbol{x})\)一个n*n的矩阵.其中第i,j个元素为是\(\partial f_i(\boldsymbol{x})/\partial x_j\).
牛顿法有很好的收敛性质 , 但是它在理论上要求较高,当n较大时不可接受;拟牛顿法就类似于单变量情形的割线法 , 采用某些近似方式逼近导数 , 在不精确计算导数的情形下尽量保持较快的收敛速度
例题-推导迭代格式
使用Gs方法,不动点法,牛顿法计算非线性方程组的根
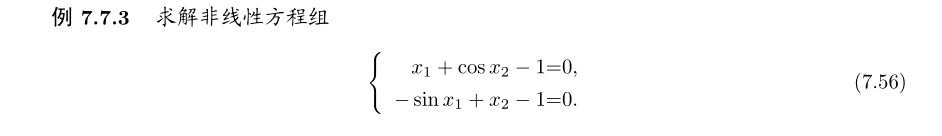
一:不动点法迭代格式
- 核心思想
基于向量函数 \(F(\boldsymbol{x})=(f_1(\boldsymbol{x}),f_2(\boldsymbol{x}),\cdots,f_n(\boldsymbol{x}))^\mathrm{T}:\mathbb{R}^n\to\mathbb{R}^n,\text{ 其中 }f_i(\boldsymbol{x})=f_i(x_1,x_2,\cdots,x_n)\) 是 x 的函数;找到不动点函数\(x=\varphi(x)\),等价于\(F(x)=\boldsymbol{0}\).
- 迭代格式
将\(F(x)=0\)左右移动后有:
因此,迭代格式\(\mathbf{x}^{(k+1)}=\mathbf{\Phi (x^k)}\)为:
二:GS法迭代格式
如果迭代第k步得到\(x^k=(x_1,x_2,\cdots,x_n)\),那么计算下一步的\(x^{k+1}\)时,需要循环\(f_i(x)\),从\(x_1,x_2...\)不断更新,直到收敛.
- 迭代格式
将不动点迭代中的公式1改写后即可得到GS法的迭代格式:
三:牛顿法迭代格式
牛顿法本质是在\(x^k\)处泰勒公式的使用,求解\(F(x)\)在\(x^k\)处的近似值,然后用近似值来更新\(x^{k+1}\).
- 迭代格式
牛顿法的迭代格式为:
python实现
点击展开
# 例题7.7.3
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
def gf(x:list)->np.ndarray:
# 原函数
x1=x[0]+np.cos(x[1])-1
x2=x[1]-np.sin(x[0])-1
return np.array([x1,x2])
def gf1(x0:list)->np.ndarray:
# 不动点法迭代格式
x1,x2=x0
return np.array([1-np.cos(x2),1+np.sin(x1)])
def gf2(x0:list)->np.ndarray:
# GS法迭代格式
x1=1-np.cos(x0[1])
x2=1+np.sin(x1)
return np.array([x1,x2])
def gf3(x0:list)->np.ndarray:
# 牛顿法迭代格式
xk=np.array(x0)
J=np.array([[1,-np.sin(xk[1])],
[np.cos(xk[0]),1]])
return xk-np.linalg.inv(J).dot(gf(xk))
def Iter(f,IterFormatFunc,x0:np.ndarray,
maxiter:int=200,tol:float=1e-10)->tuple:
# 迭代过程中的残差,解向量
res,xs=[],[]
xs.append(x0)
res.append(np.linalg.norm(f(x0)))
while True:
x_next=IterFormatFunc(x0)
# f(x0)残差,解向量
xs.append(x_next)
res.append(np.linalg.norm(f(x_next)))
if np.linalg.norm(f(x_next))<tol:
break
else:
x0=x_next
if len(res)>maxiter:
break
return xs,res
# 初值
x0=[0,0]
maxiter=100
tol=1e-10
x1,res1=Iter(gf,gf1,x0,maxiter,tol)
x2,res2=Iter(gf,gf2,x0,maxiter,tol)
x3,res3=Iter(gf,gf3,x0,maxiter,tol)
# 绘图
plt.plot(list(range(len(res1))),res1,label=f'Fix Piont Iter,num:{len(res1)}',marker='o')
plt.plot(list(range(len(res2))),res2,label=f'GS Iter,num:{len(res2)}',marker='s')
plt.plot(list(range(len(res3))),res3,label=f'newton Iter,num:{len(res3)}',marker='D')
# plt.plot(np.array(xs)[:,0],np.array(xs)[:,1],label=f'iter num:{len(res1)}')
plt.xlabel('iteration')
plt.ylabel('residual-norm(F(x))')
plt.legend()
plt.title('residual-norm VS iteration')
plt.show()
print(f"results:")
print(f"+ Fix Piont Iter,num:{len(res1)},root:{x1[-1]},residual-norm:{res1[-1]}")
print(f"+ GS Iter,num:{len(res2)},root:{x2[-1]},residual-norm:{res2[-1]}")
print(f"+ newton Iter,num:{len(res3)},root:{x3[-1]},residual-norm:{res3[-1]}")
results:
- Fix Piont Iter,num:31,root:[1.40339571 1.98602121],residual-norm:5.932554447696248e-11
- GS Iter,num:17,root:[1.40339571 1.98602121],residual-norm:5.428435478904703e-11
- newton Iter,num:25,root:[1.40339571 1.98602121],residual-norm:4.690248189831436e-11

1.4 拟牛顿法框架
1.4.1 基本思想
在空间\(\mathbb{R}^n\times\mathbb{R}^n\),取两点\((x^1,F^1),(x^2,F^2),F^1=F(x^1),F^2=F(x^2)\),可以看到 , 该方程在退化到单变量时 , 就相当于用割线斜率代替切线斜率. 多变量情形下 , 这个方程就称为拟牛顿方程 , 此时用满足拟牛顿方程的矩阵B来代替向量函数F(x) 的雅可比矩阵J.

现在讨论B矩阵的计算,设 \((x^{(k)} ,F^{(k)} ), (x^{(k+1)} ,F^{(k+1)} )\)分别是第 k 步和 k + 1 步的点.当第 k 步迭代完成后,要更新矩阵B,保证拟牛顿方程 \(F^{(k+1)}-F^{(k)}=B(x^{(k+1)}-x^{(k)})\) 成立;
记第k 步和第 k+1 步的拟牛顿矩阵分别为\(B_{k}\text{ 和 }B_{k+1}.\)称从\(B_k\)得到\(B_{k+1}\)的公式称为拟牛顿修正公式.一般地 , 在拟牛顿方法中 , 记\(s^{(k)}=x^{(k+1)}-x^{(k)},\text{记 }y^{(k)}=\boldsymbol{F}^{(k+1)}-\boldsymbol{F}^{(k)}.\boldsymbol{s}^{(k)}\text{ 也称为位移}.\)
1.4.2 拟newton算法迭代格式
满足拟牛顿方程的矩阵可以有无穷多个,常用的修正公式有:
- 秩一修正 (Rank 1 Update) 公式
- BFGS(Broyden-Fletcher-Goldfarb-Shanno) 修正公式

在上面的算法中 , 第 (4) 步 \(λ_k\) 可以恒取 1 或者可以每步调节,相当于牛顿法和牛顿下山法中的参数λ. 调节的方式也和牛顿下山法类似;在初始步中 , \(B_0\) 一般取为单位矩阵;
不仅可以节省存储 , 而且由于下面叙述的一些原因 , 甚至可以不计算 B_k 的逆
- 例题7.7.4:使用拟newton法求解例题7.7.3的根
python code
# 使用拟newton法求解例题7.7.3的根
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
from numpy.linalg import inv,norm
def F(x:list)->np.ndarray:
# 原函数
x1=x[0]+np.cos(x[1])-1
x2=x[1]-np.sin(x[0])-1
return np.array([x1,x2])
x0=np.array([0,0])
B0=np.array([[1,0],[0,1]])
maxiter=100
tol=1e-10
k=0
lamda=1
xs,res=[],[]
xs.append(x0)
res.append(norm(F(x0)))
while True:
if norm(F(x0),2)<tol:
break
if k>=1 :
if norm(np.array(xs[-1])-np.array(xs[-2]),2)<tol:
break
# 计算B_k*s^k=-F(x^k)
s0=-1*inv(B0).dot(F(x0))
x_next=x0+lamda*s0
y0=F(x_next)-F(x0)
# 修正B_k
# 秩1修正公式
B_next=B0+((y0-B0.dot(s0)).dot(s0.T))/(s0.T.dot(s0))
# BFGS(Broyden-Fletcher-Goldfarb-Shanno) 修正公式
# s0=s0.reshape(-1,1).copy()
# y0=y0.reshape(-1,1).copy()
# B_next=B0-(B0.dot(s0).dot(s0.T).dot(B0))/(s0.T.dot(B0).dot(s0))+(y0.dot(y0.T))/(s0.T.dot(y0))
if k>maxiter:
break
else:
B0=B_next
x0=x_next
k+=1
xs.append(x0)
res.append(norm(F(x0),2))
# 绘图
plt.plot(list(range(len(res))),res,label=f' quasi-newton method Iter,num:{len(res)}',marker='o')
plt.xlabel('iteration')
plt.ylabel('residual-norm(F(x))')
plt.legend()
plt.title('residual-norm VS iteration')
plt.show()
print(f"results:")
print(f"+ quasi-newton method Iter,num:{len(res)},root:{xs[-1]},residual-norm:{res[-1]}")
results:
- quasi-newton method Rank1-formula Iter,num:32,root:[1.40339571 1.98602121],residual-norm:5.932554447696248e-11
results: - quasi-newton method BFGS-formula Iter,num:17,root:[1.40339571 1.98602121],residual-norm:8.116594825464684e-13
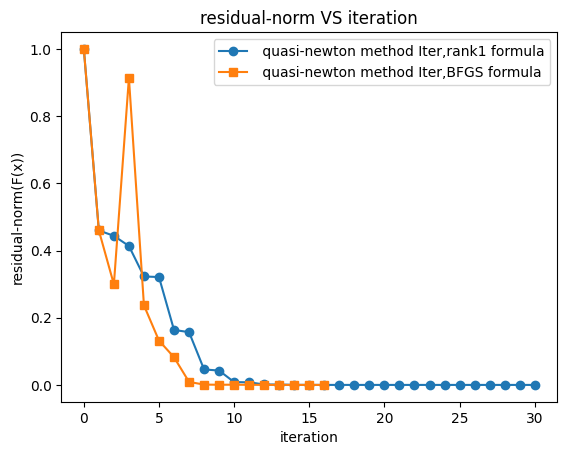
1.4.3 改进拟newton算法的迭代格式

重要应用是当 m 远小于 n 时 ,本来需要计算一个 n 阶矩阵的逆 , 利用这个公式则仅需要计算一个 m 阶矩阵的逆
记拟牛顿算法中的矩阵 \(B_k^{-1}=H_k\) , \(B_{k+1}^{-1}=\)H_{k+1}$ , 利用上述定理可以导出从 \(H_k\) 到 \(H_{k+1}\) 的修正公式
对应于上面的秩一修正 , 逆矩阵的修正公式为
对应于上面的 BFGS 修正 , 逆矩阵的修正公式为
这样 , 上述的拟牛顿方法就可以改造成如下的方法

在每一迭代步中不需去计算一个线性方程组的解
- 例题7.7.4:使用改进拟newton法求解例题7.7.3的根
python code
# 使用改进拟newton法求解例题7.7.3的根
from formu_lib import *
import numpy as np
from matplotlib import pyplot as plt
from numpy.linalg import inv,norm
def F(x:list)->np.ndarray:
# 原函数
x1=x[0]+np.cos(x[1])-1
x2=x[1]-np.sin(x[0])-1
return np.array([x1,x2])
x0=np.array([0,0])
H0=np.array([[1,0],[0,1]])
maxiter=100
tol=1e-10
k=0
lamda=1
xs,res=[],[]
xs.append(x0)
res.append(norm(F(x0)))
while True:
if norm(F(x0),2)<tol:
break
if k>=1 :
if norm(np.array(xs[-1])-np.array(xs[-2]),2)<tol:
break
# 计算s^k=-H_k*F(x^k)
s0=-1*H0.dot(F(x0))
x_next=x0+lamda*s0
y0=F(x_next)-F(x0)
# 修正H_k
s0=s0.reshape(-1,1).copy()
y0=y0.reshape(-1,1).copy()
# 秩1修正公式
H_next=H0+((s0-H0.dot(y0)).dot(s0.T).dot(H0))/(s0.T.dot(H0).dot(y0))
# BFGS(Broyden-Fletcher-Goldfarb-Shanno) 修正公式
# H_next=H0-(H0.dot(y0).dot(s0.T)+s0.dot(y0.T).dot(H0))/(y0.T.dot(s0))+(1+(y0.T.dot(H0).dot(y0))/(y0.T.dot(s0)))*((s0.dot(s0.T))/(y0.T.dot(s0)))
if k>maxiter:
break
else:
H0=H_next
x0=x_next
k+=1
xs.append(x0)
res.append(norm(F(x0),2))
# 绘图
plt.plot(list(range(len(res))),res,label=f' quasi-newton method Iter,num:{len(res)}',marker='o')
plt.xlabel('iteration')
plt.ylabel('residual-norm(F(x))')
plt.legend()
plt.title('residual-norm VS iteration')
plt.show()
print(f"results:")
print(f"+ quasi-newton method Iter,num:{len(res)},root:{xs[-1]},residual-norm:{res[-1]}")
results:
- improved quasi-newton method Iter Rank1 formula,num:14,root:[1.40339571 1.98602121],residual-norm:1.4907178785854982e-11
- improved quasi-newton method Iter BFGS formula ,num:17,root:[1.40339571 1.98602121],residual-norm:8.116594825464684e-13
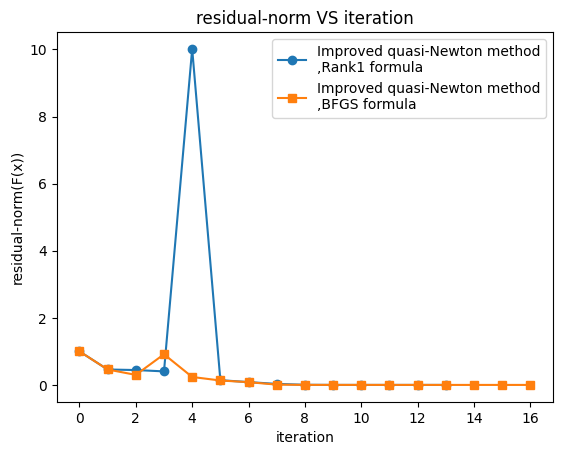
非线性最小二乘问题
下面讨论一般的非线性最小二乘问题及其常用的算法
假设有数据\((t_i,y_i),i=1,2,...,n\) , 需要找到特定形式的函数\(y=f(x)\),使之能够反映出这些数据,以下误差最小:
假设有某一非线性最小二乘问题 , 其拟合函数为\(y=f(t,x_1,x_2...x_n)\),需要拟合数据\((t_i,y_i),i=1,2,...,n\) , 此时需要求解如下最小化问题:
稳定点的条件为:
\(\text{记 }r_i(\boldsymbol{x})=y_i-f(t_i,x_1,x_2,\cdots,x_n),\text{且 }r(\boldsymbol{x})=(r_1(\boldsymbol{x}),r_2(\boldsymbol{x}),\cdots,r_n(\boldsymbol{x}))^\mathrm{T}\) 是一个向量函数 , 则\(F(x)=\frac{1}{2}r(\boldsymbol{x})^{\mathrm{T}}r(\boldsymbol{x}).\),稳定点条件等价于:
总结,公式(9)的求解,等价于求解非线性方程组\(F'(x)=0\)的根,可以采用牛顿法:
由于矩阵 \(J(x)^T J(x)\) 至少是半正定的 ,可以忽略F''(x)第二项.

如果\(J(x)^T J(x)\)可逆的条件不成立 , 或者问题本身使得 \(F'' (x)\) 的第二项不能够忽略 ,通常可以采用Levenberg-Marquardt 算法 , 或者简称 LM 算法

大范围求解方法
一个算法的局部收敛性总是比全局收敛性容易验证 , 但是我们没有很好的方法确定一个初始点怎样才算是足够靠近解 , 使得我们可以确保迭代收敛
大范围求解方法就是一种把近似解引导向精确解或者足够精确的近似解的方法 . 下面介绍的同伦算法是其中的一种
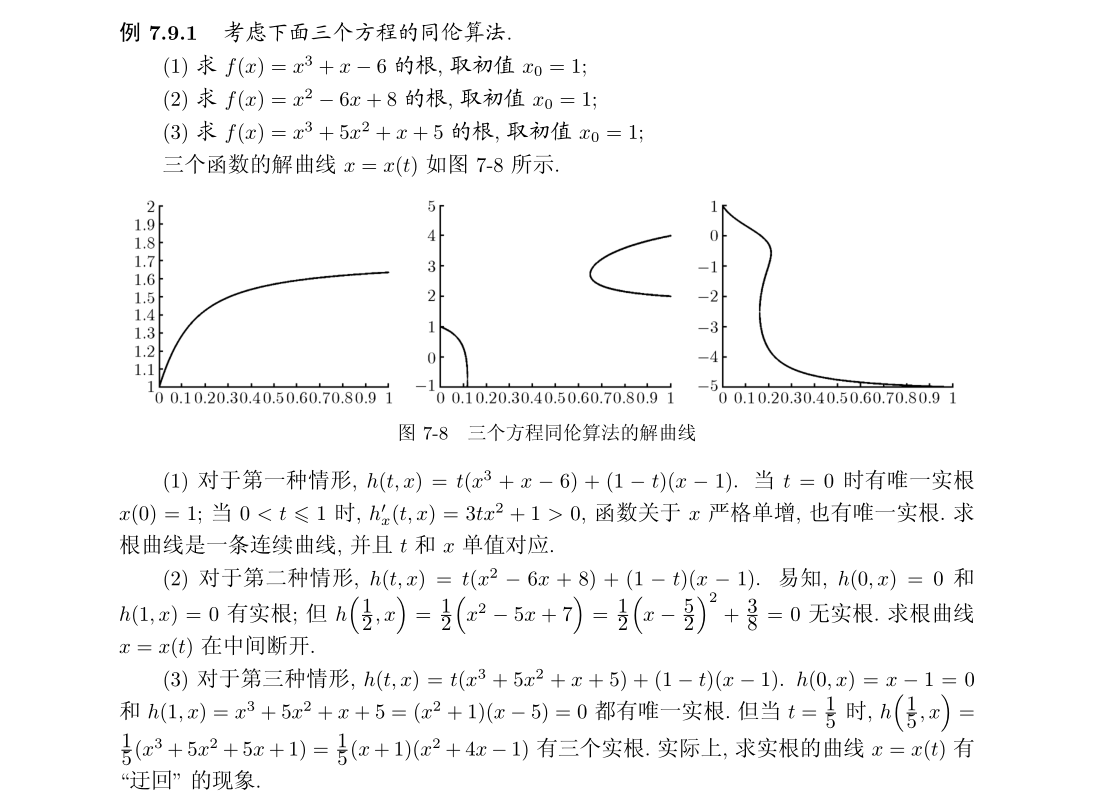
假设要求解非线性方程\(f(x)=0\),而已知\(g(x)=0\)的根.比如已知\(f(x)=0\)的近似根为a,可以令\(g(x)=x-a\),先令\(h(t,x)=tf(x)+(1-t)g(x)\),则有:
若对于任意参数\(t \in [0,1]\),记方程\(h(t,x)=0\)的解为\(x(t)\),在某些条件下,\(x(t)\)是t的连续函数而x(0)就是g(x)=0的根., 我们可以采取顺藤摸瓜的方法 , 令 t 从 0 到 1 逐渐增大 , 从而求得 x(1), 也就是方程 f(x) = 0 的根
总结
作为非线性问题的算法 , 我们总是期望在问题退化为线性时 , 算法能有极其快速的收敛 ,甚至有限步或一步就收敛 , 这样 , 当问题的非线性不是很严重时 , 算法也能有非常满意的效果
本文来自博客园,作者:FE-有限元鹰,转载请注明原文链接:https://www.cnblogs.com/aksoam/p/18348423

 二分法,不动点迭代法等
二分法,不动点迭代法等
