【数值计算方法】线性方程组的迭代解法

第6章 线性方程组的迭代解法

graph LR A[迭代法] --> B[定常迭代法] A --> C[不定常迭代法] B-->D[雅可比Jacobi迭代法] B-->E[高斯赛德尔Gauss-Seidel迭代法] B-->F[超松弛SOR迭代法] C-->G[共轭梯度法] C-->I[最速下降法] C-->H[广义极小残量法] I-->J[求解对称正定线性方程组] G-->J H-->J1[求解不对称线性方程组] A-->K[线性方程组的预处理技术] K-->L[左预处理技术] K-->M[对称预处理技术] K-->N[右预处理技术]

1. 范数和条件数

线性方程组的解是一个向量 , 称为解向量. 近似解向量与精确解向量之差成为近似解的误差向量. 范数:衡量向量和矩阵大小的度量概念

1.1 向量和矩阵的范数

img

img

矩阵的 F 范数是向量 2 范数的直接推广 , 矩阵的 2 范数的计算是 \(A^T A\) 的谱半径的开方 , 所以又称为谱范数

对于矩阵A和向量x,如果满足:

\[\|Ax\|\leqslant\|A\|\cdot\|x\| \]

则称向量范数和矩阵范数相容.常用的范数相容关系有:

\[\begin{gathered} \|Ax\|_{1}\leqslant \|A\|_1\cdot\|x\|_1, \\ \|Ax\|_{\infty}\leqslant \|A\|_\infty\cdot\|x\|_\infty, \\ \|Ax\|_{2}\leqslant \|A\|_{2}\cdot\|x\|_{2}, \\ \|Ax\|_{2}\leqslant \|A\|_{F}\cdot\|x\|_{2}. \end{gathered}\]

1.2 条件数和扰动分析

对于线性方程组:

\[Ax=b \]

解向量x由A,x决定.当A,b受到微小扰动时,对解x的扰动不一定也是微小的.无论方程组中的系数矩阵 A 有扰动 , 还是右端 b 有扰动 , 解 x 的相对误差除了受相应扰动的相对误差以外 , 还与 \(||A||*||A^{-1}||\) 的大小有关

img

对于一个确定的线性方程组 , 若系数矩阵A的条件数相对地小 , 就称方程组是良态的 ,矩阵为良态矩阵 ; 反之 , 条件数相对地大 , 就称方程组病态 , 矩阵为病态矩阵.

使用稳定方法求病态方程组的解,结果可能很差.

img

2. 基本迭代法

2.1 迭代法基本思路

对于线性方程组:

\[Ax=b \]

其中,\(A\in \mathbb{R}^{n\times n}\),\(\boldsymbol{b} \in \mathbb{R}^n\) 已知,求解\(x\in\mathbb{R}^n\)

假定A以下分解,M为非奇异方阵:

\[A=M-N \]

则有以下关系:

\[Mx=Nx+b 或者 x=Bx+g \]

其中,\(B=M^{-1}N ， g=M^{-1}b.\) 从而可以建立迭代公式:

\[x^{(k+1)}=Bx^{(k)}+g\tag{1} \]

给定初始向量 \(x^{(0)}\) ,进行迭代,就可以得向量序列 \({x^{(k)}}\) .若该序列收敛于一个确定的值 \(x^*\).则\(x^{*}=Bx^{*}+g\),也就是\(Ax^*=b\),\(x^*\)就是线性方程组的解.

初值\(x^{(0)}\)可以任意取,但一般取\(x^{(0)}=0\)或\(x^{(0)}=b\).

判断是否收敛的标准:

计算出\(x^{k+1}\)后,计算\(error=\frac{||b-A*x^{k+1}||}{||b||}\) ,若\(error\)小于某个给定的阈值,则认为迭代收敛.

以上就是解线性方程组的基本迭代解法

在公式(1)中,为了避免B,g中的求逆计算 , 我们可以按如下方式进行迭代:

\[Mx^{(k+1)}=Nx^{(k)}+b.\tag{2} \]

只是,这就每次迭代就需要求解一个系数矩阵为 M 的线性方程组\(Mx^{(k+1)}=b'\).如果M矩阵具有特殊性质(对角阵,上三角阵等),这样的方程组易于求解.如:

\[A=D-L-U \]

分别是对角矩阵、严格下三角矩阵和严格上三角矩阵:

\[\begin{gathered} D=\mathrm{diag}(a_{11},a_{22},\cdots,a_{nn}), \\ \boldsymbol{L}=-\begin{pmatrix}0&0&\cdots&0\\a_{21}&0&\cdots&0\\\vdots&\ddots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&0\end{pmatrix}, \\ \boldsymbol{U}=-\left(\begin{matrix}{0}&{{a_{12}}}&{\cdots}&{{a_{1n}}}\\{\vdots}&{\ddots}&{\ddots}&{\vdots}\\{0}&{\ddots}&{\ddots}&{{a_{n-1,n}}}\\{0}&{0}&{\cdots}&{0}\\\end{matrix}\right), \end{gathered}\]

下面介绍三种基本迭代解法：雅可比迭代法、高斯–赛德尔迭代法和SOR迭代法, 并对它们的适用性、收敛性质和收敛速度

2.2 雅可比迭代法

在公式(2)中,取\(M=D\),\(N=L+U\),就可以得到雅可比迭代法的迭代公式:

\[D\boldsymbol{x}^{(k+1)}=(\boldsymbol{L}+\boldsymbol{U})\boldsymbol{x}^{(k)}+\boldsymbol{b}.\tag{3} \]

img

2.3 高斯–赛德尔迭代法

高斯-赛德尔迭代法(简称GS迭代法)的迭代格式为:

\[Dx^{(k+1)}=Lx^{(k+1)}+Ux^{(k)}+b.\\(D-L)x^{(k+1)}=Ux^{(k)}+b. \]

img

2.4 超松弛 (SOR) 迭代法

GS 迭代格式可以改写成:

\[\begin{aligned}x^{(k+1)}&=D^{-1}(Lx^{(k+1)}+Ux^{(k)}+b)\\&=\boldsymbol{x}^{(k)}+\boldsymbol{D}^{-1}(\boldsymbol{L}\boldsymbol{x}^{(k+1)}+\boldsymbol{U}\boldsymbol{x}^{(k)}-\boldsymbol{D}\boldsymbol{x}^{(k)}+\boldsymbol{b}).\end{aligned} \]

为了加快迭代的收敛速度 , 将上式等号右端的第二项\(D^{-1}(Lx^{(k+1)}+Ux^{(k)}-Dx^{(k)}+b).\)看成是修正量,引入超松弛因子\(omega\) , 并将修正量乘上\(omega\) , 得到修正后的迭代格式:

\[x^{(k+1)}=\boldsymbol{x}^{(k)}+\omega\boldsymbol{D}^{-1}(\boldsymbol{L}\boldsymbol{x}^{(k+1)}+\boldsymbol{U}\boldsymbol{x}^{(k)}-\boldsymbol{D}\boldsymbol{x}^{(k)}+\boldsymbol{b}),\\x^{(k+1)}=(\boldsymbol{D}-\omega\boldsymbol{L})^{-1}[(1-\omega)\boldsymbol{D}+\omega\boldsymbol{U}]\boldsymbol{x}^{(k)}+\omega(\boldsymbol{D}-\omega\boldsymbol{L})^{-1}\boldsymbol{b}. \]

这就是逐次超松弛迭代法 , 简称SOR迭代法.

img

2.5 迭代的收敛性分析和误差估计

  • 定理 6.2.10

迭代格式 (1), 给定任意的初值 x(0) , 有下列收敛结果和误差估计：

  1. 迭代格式 (1) 收敛的充要条件为谱半径 $$\rho(B) < 1$$
  2. 若\(||B||<1\),则有误差估计:

\[\|x^{(k)}-x^*\|\leqslant\frac{\|B\|^k}{1-\|B\|}\|x^{(1)}-x^{(0)}\| \]

\[\|x^{(k)}-x^*\|\leqslant\frac{\|B\|}{1-\|B\|}\|x^{(k)}-x^{(k-1)}\|.\tag{4} \]

其中 , \(x^∗\) 为 \(Ax=b\) 的真解

  • 定理 6.2.11

若 A 是严格对角占优或不可约弱对角占优矩阵 , 则雅可比迭代和 GS 迭代都收敛.

  • 定理 6.2.12

若 A 是对称正定矩阵 , 则雅可比迭代收敛的充要条件是 \(2D − A\) 也是对称正定矩阵

  • 定理 6.2.13

SOR 迭代收敛的必要条件是 0 < ω < 2.

  • 定理 6.2.14

设系数矩阵 A 对称正定 , 则 0 < ω < 2 时 SOR 迭代收敛

3. 不定常迭代法

本节将介绍两类最基本的不定常迭代方法：一类是求解对称正定线性方程组的最速下降法和共轭梯度法; 另一类是求解不对称线性方程组的广义极小残量法

3.1 最速下降法

img

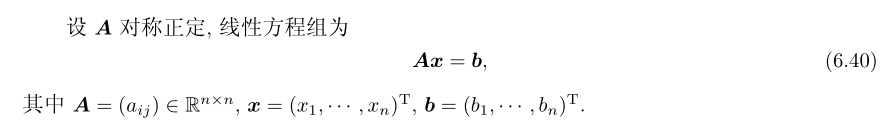
对于\(x\),定义n元二次函数:\(\varphi:\mathbb{R}^{n}\to\mathbb{R}\),

\[\varphi(x)=\frac12(\boldsymbol{x},\boldsymbol{A}\boldsymbol{x})-(\boldsymbol{x},\boldsymbol{b}),\text{其中,}(x,y)=\sum_{i=1}^{n}x_{i}y_{i}. \]

  • 定理 6.3.1

设 A 对称正定 , \(x^∗\) 是方程组 Ax = b 的解的充要条件是 \(x^∗\)为二次函数ϕ(x)的极小值点 , 即

\[\varphi(\boldsymbol{x}^*)=\min_{\boldsymbol{x}\in R^n}\varphi(\boldsymbol{x}). \]

定理 6.3.1 将求解方程组 Ax = b 的问题转化为求函数 ϕ(x) 的为唯一极小点的问题

为了找到 ϕ(x) 的极小点 \(x^∗\) ,可以从任一点 \(x^(k)\)出发 , 沿某一指定的方向\(y^{(k)}\in\mathbb{R}^n\)搜索下一个近似点\(x^{(k+1)}=x^{(k)}+\alpha_{k}y^{(k)},\)使得\(\varphi(x^{(k+1)})\)在该方向上达到极小值.

选择\(y^{(k)}\)的方式不同时 , 将会得到不同的算法.

令 \(y^(k)\) 为某一搜索方向,\(r^{(k)}=b-Ax^{(k)}\)为\(x^{(k)}\)对应的残量.则有:

\[\varphi(\boldsymbol{x}^{(k)}+a\boldsymbol{y}^{(k)})=\varphi(\boldsymbol{x}^{(k)})-a(\boldsymbol{y}^{(k)},\boldsymbol{r}^{(k)})+\frac12a^2(\boldsymbol{y}^{(k)},\boldsymbol{A}\boldsymbol{y}^{(k)}).\tag{5} \]

根据二次函数性质可知:

\[a_k=\frac{(\boldsymbol{y}^{(k)},\boldsymbol{r}^{(k)})}{(\boldsymbol{y}^{(k)},\boldsymbol{A}\boldsymbol{y}^{(k)})}. \]

\(a_k\)是\(\varphi(x^{(k)}+a\boldsymbol{y}^{(k)})\)的极小点.将\(a_k\)代入上式(5),有:

\[\varphi(\boldsymbol{x}^{(k)}+a_k\boldsymbol{y}^{(k)})-\varphi(\boldsymbol{x}^{(k)})=-\frac{1}{2}\frac{(\boldsymbol{y}^{(k)},\boldsymbol{r}^{(k)})^2}{(\boldsymbol{y}^{(k)},\boldsymbol{A}\boldsymbol{y}^{(k)})}.\tag{6} \]

\(\text{当 }(\boldsymbol{r}^{(k)},\boldsymbol{y}^{(k)})\neq0,\text{ 即 }\boldsymbol{y}^{(k)}\text{ 不与 }\boldsymbol{r}^{(k)}\text{ 正交时, }\varphi(\boldsymbol{x}^{(k+1)})<\varphi(\boldsymbol{x}^{(k)})\text{ 成立}.\)

从公式(6)可以看出,每次迭代后\(\varphi(x^{(k+1)})\)的下降量只取决于\(y^{(k)}\)的方向,而与\(y^{(k)}\)无关.函数 ϕ(x) 在点 \(x^{(k)}\)处下降最快的方向应该是在该点的负梯度方向,即\(r^{(k)}\)

每次迭代,取\(y^{(k)}=r^{(k)}\)作为搜索方向,然后构造\(x^{(k+1)}=x^{(k)}+a_k r^{(k)}\),可以计算出\(\varphi(x)\)的极小点的最速下降法

img

3.1.1 最速下降法的误差估计

  • 定理 6.3.4

设 A 是 n 阶实对称正定矩阵,\(\lambda_{1}\)和\(\lambda_{n}\)分别是A的最大,最小特征值.则由最速下降法得到的迭代序列 \({x^{(k)}}\) 满足误差估计:

\[\left\|x^{(k)}-x^*\right\|_A\leqslant\left[\frac{\lambda_1-\lambda_n}{\lambda_1+\lambda_n}\right]^k\left\|x^{(0)}-x^*\right\|_A.\tag{7} \]

由误差估计式(7) 可得最速下降法的收敛性.不过 , 当\(\lambda_{1}\)远远大于\(\lambda_{n}\)时,\(\frac{\lambda_1-\lambda_n}{\lambda_1+\lambda_n}\approx1,\)这时 , 最速下降法的收敛速度将会很慢.

3.2 共轭梯度法

对上述最速下降法作一简单分析,可以发现: 负梯度方向虽为局部最优的搜索方向 , 但从整体来看并非最优. 这就促使人们去寻找更好的搜索方向 , 当然 , 希望每一步确定新的搜索方向时付出的代价也不要太大.

共轭梯度法的思想:仍设 A 对称正定 , 我们还是采用一维极小搜索的概念 .但不再沿负梯度方向\(r^{(0)}, r^{(1)}, \cdots, r^{(k)}\)搜素,而是要另找一组方向\(p^{(0)},p^{(1)},\cdots,p^{(k)}\),使得进行 k 次一维搜索后 , 求得近似解 \(x^{(k)}\).

对一维极小问题\(\min_{\alpha}\varphi(\boldsymbol{x}^{(k)}+\alpha\boldsymbol{p}^{(k)})\),令:

\[\frac{\mathrm{d}}{\mathrm{d}\alpha}\varphi(p^{(k)}+\alpha p^{(k)})=0, \]

可得:

\[\alpha=\alpha_k=\frac{(r^{(k)},p^{(k)})}{(\boldsymbol{A}\boldsymbol{p}^{(k)},\boldsymbol{p}^{(k)})}.\tag{8} \]

从而,下一步的近似解和对应的残量分别为:

\[\boldsymbol{x}^{(k+1)}=\boldsymbol{x}^{(k)}+\alpha_{k}\boldsymbol{p}^{(k)},\\\boldsymbol{r}^{(k+1)}=\boldsymbol{b}-\boldsymbol{A}\boldsymbol{x}^{(k+1)}=\boldsymbol{r}^{(k)}-\alpha_{k}\boldsymbol{A}\boldsymbol{p}^{(k)}.\tag{9} \]

  • 定义 6.3.5

A 对称正定,若\(\mathbb{R}^n\)中向量组\(\{p^{(0)},p^{(1)},\cdots,p^{(l)}\}\)满足:

\[(Ap^{(i)},p^{(j)})=0,\quad i\neq j,/tag{10} \]

则该向量组为\(\mathbb{R}^n\)中的一个A-共轭向量组,或者称A-正交向量组,或称这些向量是A-共轭的

第一次迭代时, , 可以令 \(p^{(0)} = r^{(0)}\) .\(k>0\)时,不妨设\(p^{(k)}=r^{(k)}+\beta_{k-1}p^{(k-1)},\)利用\((p^{(k)},Ap^{(k-1)})=0,\)可以求出:

\[\beta_{k-1}=-\frac{(\boldsymbol{r}^{(k)},\boldsymbol{Ap}^{(k-1)})}{(\boldsymbol{p}^{(k-1)},\boldsymbol{Ap}^{(k-1)})}. \]

这样的得到的\(p^{(k)},p^{(k-1)}\)是A-共轭的

img

img

3.2.1 共轭梯度法的误差估计

img

当系数矩阵 A 的条件数很大时 , 共轭梯度法的收敛速度可能很慢 . 条件数较小时 , 收敛很快

3.3 广义极小残量法

广义极小残量法(Gerneral Minimal RESidual法,)是求解不对称线性方程组的一种迭代法.已经成为当前求解大型稀疏非对称线性方程组的主要手段,

本节中的范数 \(|| · ||\) 均为 2-范数 .

设所求线性方程组为

\[Ax=b, \]

取\(x^{(0)}\in\mathbb{R}^{n}\)为任一向量,令\(x=x^{(0)}+z,\)则上式等价于

\[Az=r^{(0)},/tag{11} \]

其中,\(r^{(0)}=b-Ax^{(0)}\),现在就只需要讨论公式(11)的求解问题

广义极小残量法的推导过程见<<现代数值计算第二版>>p172

img

img

3.3.1 广义极小残量法的收敛性

img

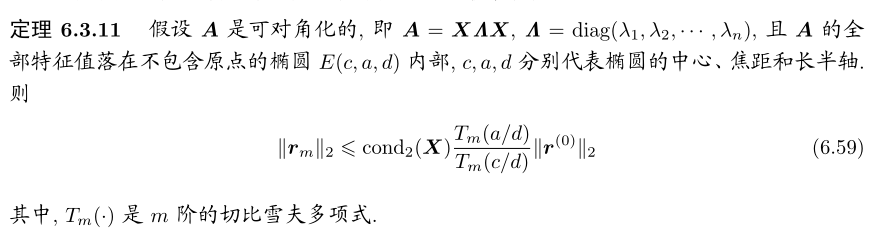
4. 预处理技术

由于存在浮点运算的误差 , 共轭梯度法和广义极小残量法计算得到的向量会逐渐失去正交性 , 因而都不能在 n 步之内得到原方程的精确解 . 况且 , 遇到求解大规模的线性代数方程组 , 即使能够在 n 步收敛的话 , 这个收敛速度也不能令人满意 . 预处理技术能有效地改善收敛性质并加快收敛速度 , 因而在实际使用中应用得非常广泛

预处理技术从广义上来说可以指对原方程组进行的任何显示的或者隐式的修正 , 使得该方程组通过迭代法更容易求解

简单地说 , 花比较小的代价找到一个矩阵 M, 然后用迭代法求解如下的同解线性方程组:

\[M^{-1}Ax=M^{-1}b, \]

或

\[AM^{-1}y=b,\quad x=M^{-1}y, \]

新得到的算法分别称为左预处理或者右预处理的迭代方法

特别地 , 如果存在矩阵L使得\(M=LL^T\),计算以下同解线性方程组:

\[L^{-1}AL^{-\mathrm{T}}y=L^{-1}b,\quad x=L^{-\mathrm{T}}y. \]

这是对称预处理方法 , 特别在预处理共轭梯度方法时经常使用 ,M称为预处理矩阵. 一个好的预处理矩阵至少能够满足如下的条件：

  • 构造 M 的代价很小 ;
  • M 跟 A 足够接近 ;
  • 关于 \(M^{−1}\) 的线性方程组很容易求解

当系数矩阵 A 的对角元非零时 , 取 M = diag(A), 我们可以得到一个最常用的预处理矩阵

img

一般认为 , 如果预处理后的系数矩阵 \(M^{−1} A\) 的特征值更加聚集的话 , 不管是用共轭梯度法还是用广义极小残量法都会得到更好的收敛效果

总结

  1. 使用各种迭代格式时 , 最主要的就是判断它的收敛性以及了解收敛速度
  2. 在实际计算中 , 对一种迭代格式 , 不必事先判断了收敛性才敢使用 , 它完全可以在计算过程中判断是否收敛
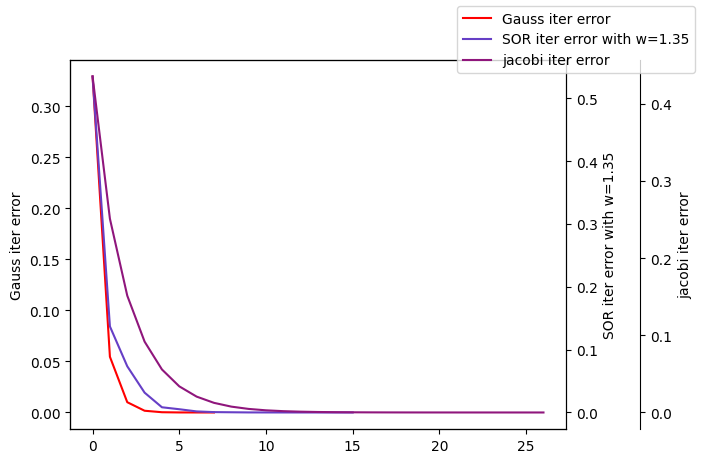
  3. 雅可比迭代与 GS 迭代的收敛域并不互相包含 , 所以不能相互代替
  4. 当两者皆收敛时 , 一般来说 GS 迭代比雅可比迭代的收敛速度快 . 实用中更多的是使用 SOR 迭代,松弛因子有赖于实际经验
  5. 共轭梯度法 ( 简称 CG 法 ) 是求解系数矩阵为对称正定的线性方程组的非常有效的方法
  6. 当 Ax = b 为病态方程组时 , cond(A) 很大 ,共轭梯度法收敛缓慢 . 这时 , 可以使用预条件共轭梯度法来计算 , 往往其收敛速度大大提高

习题

img

img

img

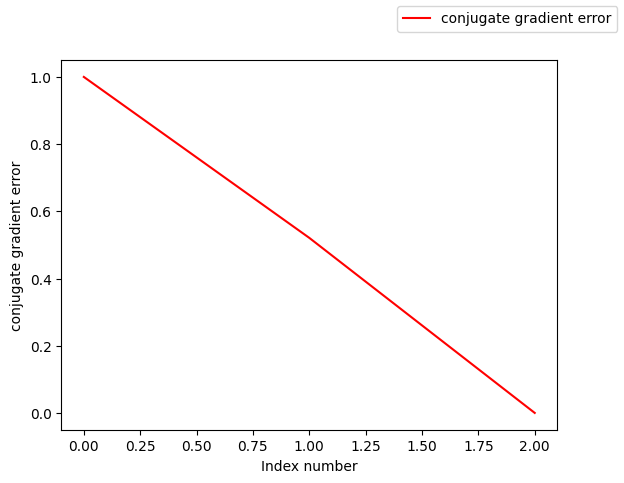
迭代次数2001,误差估计||b-Ax||/||b||=nan,不满足tol=1e-06

img

img

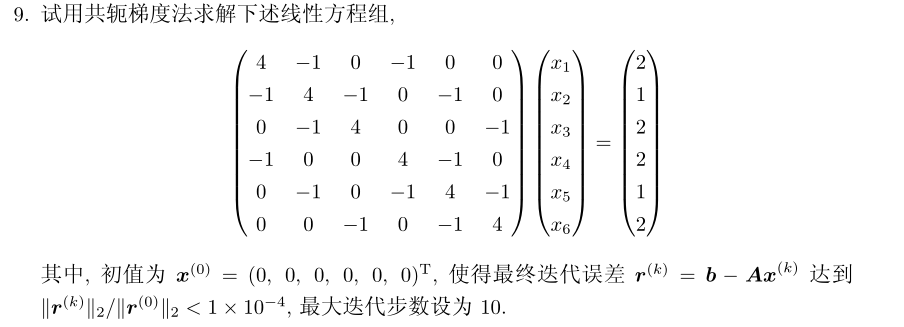
from formu_lib import *
import numpy as np
A=np.array([[4,-1,0,-1,0,0],
            [-1,4,-1,0,-1,0],
            [0,-1,4,0,0,-1],
            [-1,0,0,4,-1,0],
            [0,-1,0,-1,4,-1],
            [0,0,-1,0,-1,4]])
b=np.array([2,1,2,2,1,2])

x1,er1=conjGrad(A,b,1e-8)

plotLines([list(range(len(er1))),],[er1,],["conjugate gradient error"])

img

posted @ 2024-08-06 16:42  FE-有限元鹰  阅读(123)  评论(0)  编辑  收藏  举报