240720-模态应变法计算阻尼-论文阅读

技术报告:NASA-Computational Simulation of Damping in Composite Structures

目录

• 技术报告:NASA-Computational Simulation of Damping in Composite Structures
  • 摘要
  • METHOD
    • lamnate damping
    • 结构模态阻尼
• NASA技术报告-Extracting Damping Ratio From Dynamic Data and Numerical Solutions
  • 摘要
  • 提取阻尼比的数值方法
• NASA技术报告-MODAL STRAIN ENERGIES IN COSMIC NASTRAN
  • 摘要
  • 模态应变能计算
  • 阻尼比计算
• 国家标准文件: GB/T18258-2000 阻尼材料-阻尼性能测试方法
  • 测试方法
  • 测试数据

摘要

• 提出了一种复合材料结构被动阻尼预测的计算方法。
• 该方法综合了微观力学、层压理论和结构阻尼理论，建立了多级阻尼模型。
• 采用有限元离散化方法对结构层面的阻尼进行了模拟。
• 论文中将这个方法应用于beam,plate ,shells

METHOD

graph LR A[on-axis damping] --> B[off-axis damping] B --> C[local laminate damping] C --> D[structural modal damping]

lamnate damping

基于多自由度动力学方程,在一个完整震动周期上积分,可以计算的到耗散应变能\(\Delta \omega\)如下,其中\([\zeta]\)为loacl damping matrix of material.

\[\Delta w=\oint\delta\epsilon^{T}[\zeta] \epsilon\quad\tag{5} \]

谐振载荷下,应变为\(\epsilon=\epsilon_\mathbf{a}\sin(\omega t)\),上式变为:

\[\Delta w=\pi\omega\epsilon_{\mathrm{a}}^{\mathrm{T}}[\zeta]\epsilon_{\mathrm{a}}\tag{6} \]

这是计算结构耗散应变能的通用公式.当考虑计算对象为复合材料层合板时,\([\zeta]\)为层合板阻尼矩阵\([\zeta_L]\);广义应变\(\epsilon_L\)为层合板的应变(包括中面应变和中面曲率):

\[\epsilon_{\mathrm{L,a}}=\{\epsilon^{0},\mathrm{k}\}=\{\epsilon^{0}_{11},\epsilon^{0}_{22},\mathrm{k}_{12},\mathrm{k}_{13},\mathrm{k}_{23}\} \]

因此,层合板的耗散应变能计算公式为:

\[\Delta w_{L}=\pi\omega\epsilon_{\mathbf{L,a}}^{\mathbf{T}}[\zeta_{L}]\epsilon_{\mathbf{L,a}} \]

根据Mechanics of damping for fiber composite laminates including hygro-thermal effects,可以计算得到层合板的阻尼矩阵\([\zeta_L]\),该阻尼矩阵由\([A_d],[D_d],[C_d]\)组成:

\[\Delta \omega _{L}=\frac{1}{2} \epsilon_{L,a}^T\begin{bmatrix} A_d & C_d \\ C_d & D_d \\ \end{bmatrix}\epsilon_{L,a}\tag{9}\]

结构模态阻尼

由于任何结构在经历小挠度时的弹性动力响应是单个振动模态的线性组合，因此与每个模态相关的结构阻尼将为复合结构的整体阻尼能力提供一个自然而有意义的度量.

模态阻尼: 表示结构在各自模态下单独振动时的阻尼能力

与第n个振动模态相关的模态比阻尼能力(SDC)\(\phi_n\)定义为:

\[\psi_n=\frac{\int_V\Delta w_ndV}{\int_Vw_ndV} \]

其中,\(\Delta \omega_n\) and \(\omega_n\) 表示每个循环的耗散和最大比模态应变能。如果计算对象为plate/shell composite structure,比阻尼能力公式为:

\[\psi_n=\frac{\int_A \Delta w_{L,n} dA}{\int_A w_{L,n} dA} \]

\(\Delta w_{Ln},w_{Ln}\) 的定义如公式(8)(9).建立有限单元模型,进行模态分析,与有限元模型集成后,比阻尼能力的计算公式为:

\[\Delta W_{e,n}=\frac12\int_{A_e}\mathbf{u_{e,n}}^T[B_e]^T\begin{bmatrix} [A_d] & [C_d] \\ [C_d] & [D_d] \end{bmatrix}[B_e]\mathbf{u_{e,n}}dA_e\]

\[W_{e,n}=\frac12\int_{A_e}\mathbf{u_{e,n}}^T[B_e]^T\begin{bmatrix} [A_s] & [C_s] \\ [C_s] & [D_s] \end{bmatrix}[B_e]\mathbf{u_{e,n}}dA_e\]

其中,\([B_e]\)为单元应变矩阵,\([A_s],[C_s],[D_s]\)为层合板刚度矩阵,\([A_d],[C_d],[D_d]\)为层合板阻尼矩阵.

\[\psi_n=\frac{\sum_{j=1}^{N_e}(\Delta W_{e,n})_j}{\sum_{j=1}^{N_e}(W_{e,n})_j}=\frac{总单元耗散能}{总单元应变能} \]

---

NASA技术报告-Extracting Damping Ratio From Dynamic Data and Numerical Solutions

link:论文链接

摘要

• 收集了从数据或数值模型中提取阻尼参数的方法。
• 为动力学分析中使用的一些更常用的方法提供了快速参考。
• 讨论了Comsol中复特征值分析提取模态阻尼的原理

提取阻尼比的数值方法

特征分析或模态分析可用于提取系统的动态特性，包括阻尼比。这可以传统地使用状态空间建模来完成，或者使用有限元方法来完成更复杂的系统。

COMSOL复特征值为:

\[\lambda_{\mathrm{COMSOL}}=\lambda_{r}+\lambda_{i}i . \]

固有频率和阻尼比为:

\[\omega_{n}=\sqrt{\lambda_{r}^{2}+\lambda_{i}^{2}}\\\zeta=\frac{\lambda_{r}}{\sqrt{\lambda_{r}^{2}+\lambda_{i}^{2}}}. \]

阻尼固有频率和有阻尼谐振角频率为:

\[\omega_{d}=\omega_{n}\sqrt{1-\zeta^{2}}=\left|\lambda_{i}\right|\\\omega_{p}=\omega_{n}\sqrt{1-2\zeta^{2}}=\sqrt{\lambda_{i}^{2}-\lambda_{r}^{2}} . \]

复特征频率很容易确定:

\[f_{\mathrm{COMSOL}}=f_{r}+f_{i}i=-\frac{\lambda_{i}}{2\pi}+\frac{\lambda_{r}}{2\pi}i . \]

因此,固有频率，阻尼比，有阻尼固有频率分别为:

\[f_{n}=\sqrt{f_{r}^{2}+f_{i}^{2}}\:, \]

\[\zeta=\frac{f_{i}}{\sqrt{f_{r}^{2}+f_{i}^{2}}}\:, \]

\[f_d=\left|f_r\right|, \]

综上,通过进行复特征值分析,可以提取模态阻尼比。

NASA技术报告-MODAL STRAIN ENERGIES IN COSMIC NASTRAN

link:论文链接

摘要

论文中提出了一种方法,基于FEM的计算模态应变能法,进而计算结构的阻尼比.

模态应变能计算

mode r的一个单元模态应变能的计算公式为:

\[ElementModalStrainEnergy=\frac{1}{2}\phi_{r}^T[k_e]\phi_{r} \]

其中:

• \(\phi_{r}\):mode-r下,单元的特征向量
• \([k_e]\):单元刚度矩阵(可以用abaqus 导出到数据文件)

检验计算结果的正确性:模态r的广义刚度\(k_i=\phi_{r}^T[K]\phi_{r}\)的\(\frac{1}{2}\)等于结构总应变能.

阻尼比计算

粘弹性材料在轻型结构中被动阻尼振动的能力是有据可查的.模态应变能在估计这类结构的阻尼时很有用。用于预测结构各模态阻尼(损失)因子的方法称为模态应变能法。

它指出，对于给定的振动模态，结构损失因子与粘弹性材料损失因子的比值可以估计为当结构变形为特定的无阻尼模态振型时，粘弹性中的弹性应变能与整个结构的总弹性应变能之比(参考文献)。这在数学上可以表述为:

\[\frac{\eta_s^{(r)}}{\eta_v}=\frac{V_v^{(r)}}{V_s^{(r)}} \]

其中:

• \(\eta_s^{(r)}\): 复合结构第r阶模态的损耗因子
• \(\eta_{v}\): 粘弹性材料的损耗因子
• \(V_{v}^{r}\): 当结构以第r阶无阻尼振型变形时，粘弹性材料中储存的弹性应变能
• \(V_{s}^{r}\): 整个复合结构在r阶振型下的弹性应变能

将粘弹性材料视为具有实刚度模量的纯弹性材料，计算复合结构的无阻尼模态振型，则有:

\[\frac{V_v^r}{V_s^r}=\frac{\sum_{\theta=1}^n\phi_\theta^{r^t}k_{e,\theta}\phi_\theta^r}{\phi^{r^t}K\phi^r} \]

其中:

• \(\phi^r\): 第r阶振型向量
• \(\phi_{\theta}^r\): subvector formed by deleting from \(\phi\) all entries not corresponding to motion of nodes of the \(\theta\) th viscoelastic element
• \(K\): 复合材料结构的整体刚度矩阵
• \(n\): 模型中粘弹性单元的个数
• \(k_{e,\theta}\): 第\(\theta\)个黏弹性单元的单元刚度矩阵

联合上式,可以得到:

\[\eta_{s}^{r}=\frac{\sum_{\theta=1}^{n}\eta_{v,\theta}(\phi_{\theta}^{r})^Tk_{e,\theta}\phi_{\theta}^{r}}{(\phi^{r})^TK\phi^{r}} \]

由此,就可以估计结构各模态阻尼(损失)因子。

国家标准文件: GB/T18258-2000 阻尼材料-阻尼性能测试方法

测试方法

标准规定了采用悬臂梁共振法测定材料振动阻尼特性的方法.

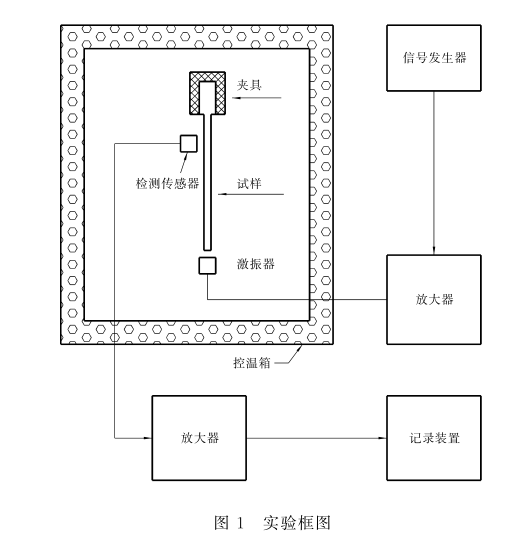
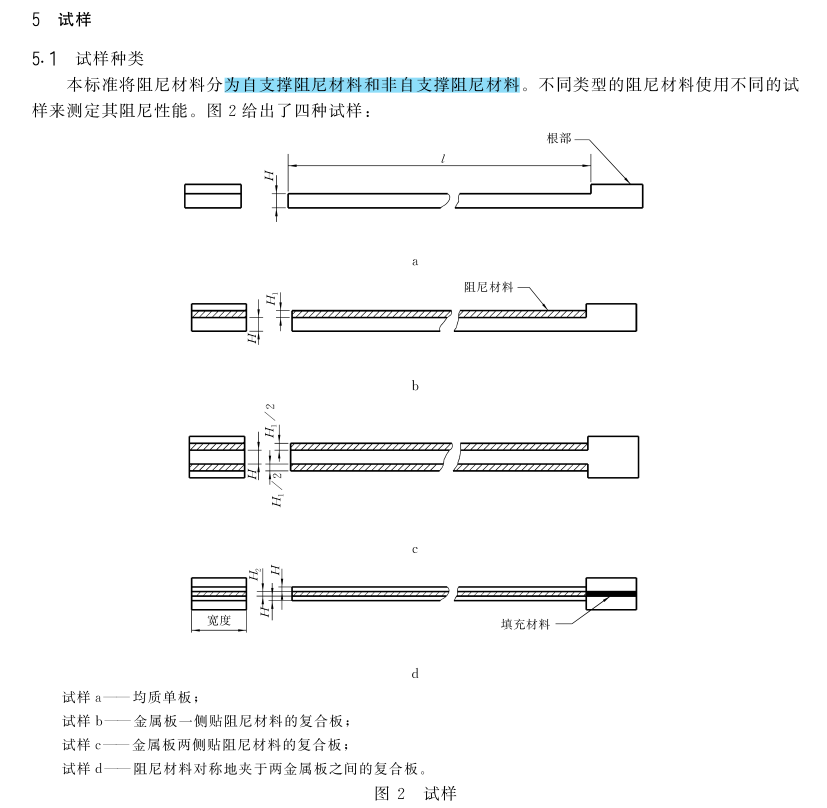
测试数据

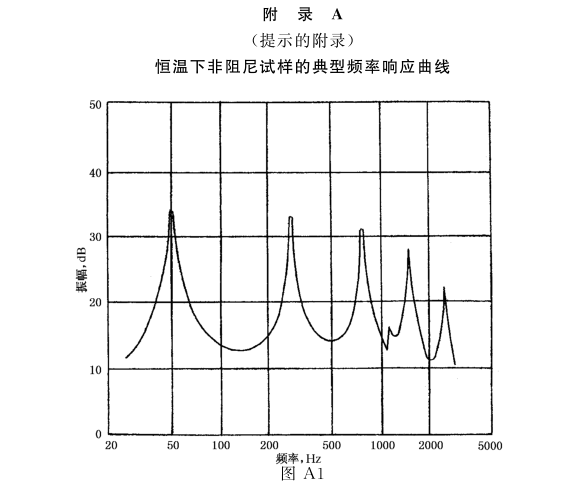
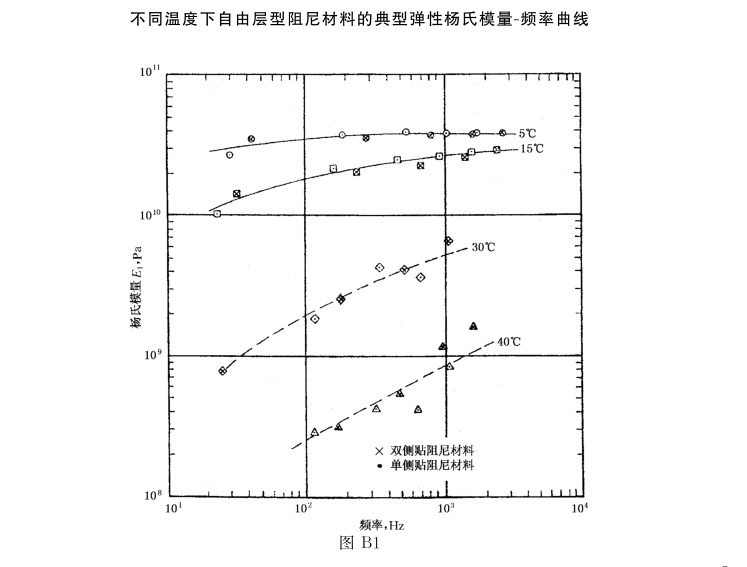
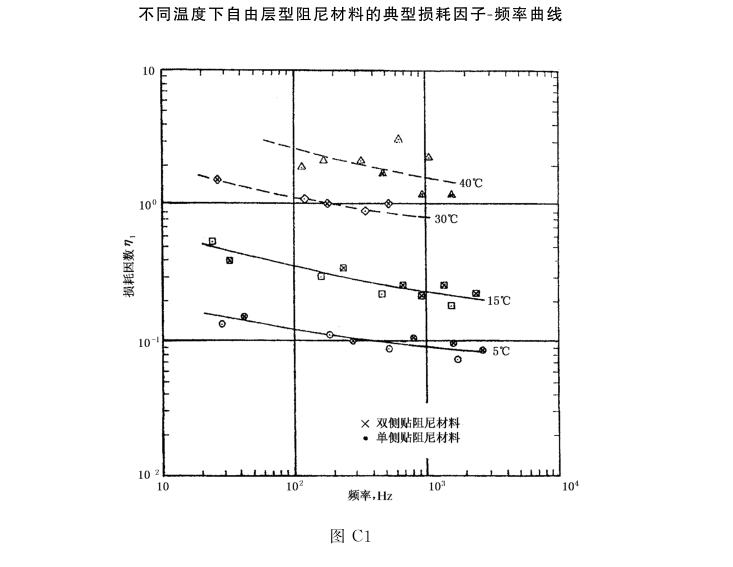
从标准文件看,国标在每个共振峰处,使用半功率法或共振放大法,计算得到阻尼比.得到的是一系列散点数据.可以拟合得到阻尼与频率的关系曲线.