结构动力学教材-学习笔记

目录

参考教材:

阻尼性能是我硕士课题的主要工作,着眼点在:如何描述符合材料结构的阻尼?什么因素影响了结构的阻尼性能大小?怎么表示阻尼性能的大小?如何计算阻尼性能?

一 阻尼模型

  • 梁超锋. 混凝土材料与结构阻尼测试、增强与表达[D]. 黑龙江:哈尔滨工业大学,2005. DOI:10.7666/d.Y820173.

二 动力学教材笔记

2.1 机构动力学概述

结构动力学是研究任何给定类型的结构在承受任意动力荷载时应力和变位的分析方法.动力载荷意为:大小、方向和作用点随时间变化的任意荷载.

分类:

  • 非随机:荷变化规律明确,但可以用统计方法进行分析
    • 周期性
    • 非周期性
  • 随机:载荷变化规律不明显,但可以用统计方法进行分析.

img

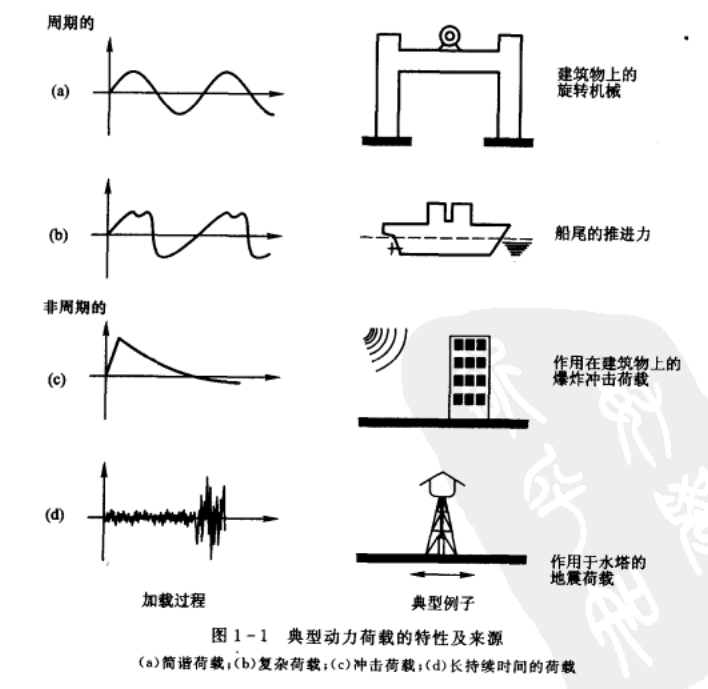
动力学问题和静力学问题的区别:

  • 静力学的解是单一解,而动力学的解是与载荷,时间有关的一系列解.
  • 动力学分析时,由于载荷与时间相关P=p(t),分析时还需要考虑惯性力(结构加速度引起的).

如果结构在p(t)作用下,运动缓慢,惯性力可以忽略,则即使结构载荷和反应与时间相关,对任何所需瞬时的分析,仍可用结构静力分析方法来解决.

2.2 单自由度体系的自由振动分析

最简单的单自由度体系:

img

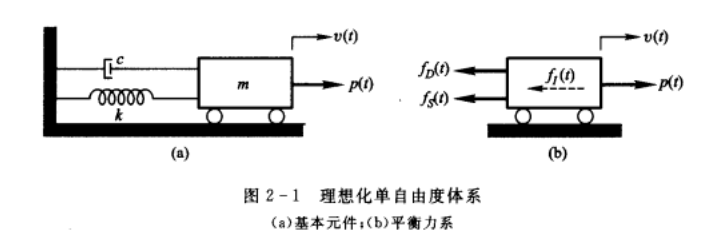
承受外部激励源或荷载的任何线性弹性结构的基本物理特性是:体系的质量m, 弹性特性(柔度或刚度)k, 能量耗散机理或阻尼c

动力学运动方程为:

\[m\ddot{v}\left(t\right)+c\dot{v}\left(t\right)+kv\left(t\right)=p\left(t\right)\tag{1} \]

2.2.1 支座激励的影响

结构的动应力和动挠度不仅可以由载荷p(t)引起,而且可以由结构支撑点运动引起.(也就是abaqus中的 base motions),地震激励就是典型的支座激励.

建立一个地震激励的简单体系:

img

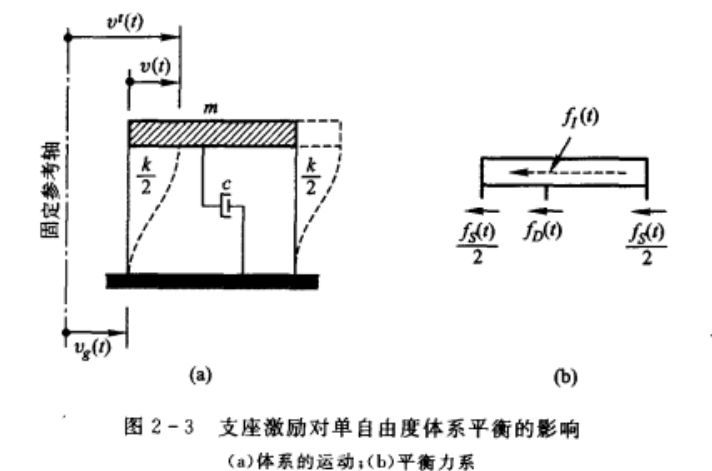
\(f_{l}(t)\)是结构的惯性力.\(v_{g}(t)\)是结构基底位移.

运动学方程为\(f_l(t)+f_D(t)+f_S(t)=0\), 弹性力项和阻尼力项和之前一致,惯性力项:\(f_{l}(t)=m\ddot{v}^{t}(t)\),\(v^{t}(t)\)表示质量对固定参考轴的总位移.总方程为:

\[m\ddot{v}^t(t)+c\dot{v}(t)+kv(t)=0 \]

将\(v^{t}(t)=v(t)+v_{s}(t)\)带入上式,得:

\[m\ddot{v}\left(t\right)+c\dot{v}\left(t\right)+kv\left(t\right)=-m\ddot{v}_{s}\left(t\right)\equiv p_{\mathrm{elf}}\left(t\right) \]

\(p_{\mathrm{elf}}\left(t\right)\)表示等效支座激励载荷.

2.2.2 无阻尼自由振动

运动方程:

\[m\ddot{v}(t)+c\dot{v}(t)+kv(t)=0 \]

自由震动的位移通解有形如:

\[v(t)=G\exp(st) \]

其中,G是任意复常数,\(G=G_R+iG_l =\overline{G}\exp(i\theta)\).将v(t)代入方程后,并引入记号:\(\omega^2\equiv\frac km\)

\[(ms^2+cs+k)G\exp(st)=0 \]

\[s^2+\frac cms+\omega^2=0\tag{2} \]

可以看出,只要求出方程的根s,就可以得到运动方程的解.而根依赖于C相对于m,k的相对值.即阻尼大小决定了体系的动力反应.

令\(c=0\),则有:\(s_{1,2}=\pm i\omega\),因此:\(v(t)=G_{1}\exp(i\omega t)+G_{2}\exp(-i\omega t)\)

讨论复常数\(G_{1},G_{2}\)的大小,有:

\[G_{1}=G_{1R}+iG_{1I};\quad G_{2}=G_{2R}+iG_{2I} \]

\[v(t)=(G_{1R}+iG_{1I})(\cos\omega t+i\sin\omega t)+(G_{2R}+iG_{2I})(\cos\omega t-i\sin\omega t) \]

\[v(t)=(G_{1R}+G_{2R})\cos\omega t-(G_{1l}-G_{2l})\sin\omega t+ i[(G_{11}+G_{21})\cos\omega t+(G_{1R}-G_{2R})\sin\omega t] \]

考虑到自由振动的结果必须是实数,因此虚部为0.即:\(G_{1I}=-G_{2I}=G_I;\quad G_{1R}=G_{2R}=G_R\).可见G1,G2互为共轭复数:\(G_{1}=G_{R}+iG_{I};\quad G_{2}=G_{R}-iG_{I}\).最终自由振动解为:

\[v(t)=(G_{R}+iG_{I})\exp(i\omega t)+(G_{R}-iG_{I})\exp(-i\omega t) \]

使用euler变换对\(v(t)\)再进行化简,得:

\[v(t)=A\cos\omega t+B\sin\omega t;\quad A=2G_R , B=-2G_I \]

通过边界条件(\(v(0),\ddot{v}(0)\)),可以确定A,B.最终,无阻尼自由振动位移解为:

\[v(t)=v(0)\cos\omega t+\frac{\dot{v}(0)}{\omega}\sin\omega t \]

img

式中:

  • \(v(0)\):初始速度
  • \(\dot{v}(0)\):初始加速度
  • \(\omega\):角频率,\(\omega=\sqrt{\frac{k}{m}}\)
  • 运动频率\(f=\frac{\omega}{2\pi}\),单位为Hz.
  • 运动周期\(\frac1f=\frac{2\pi}\omega=T\),单位为秒.

位移解的另一形式:

\[v(t)=\rho\mathrm{cos}(\omega t+\theta) \]

振幅为:

\[\rho=\sqrt{\left[v(0)\right]^{2}+\left[\frac{\dot{v}\left(0\right)}{\omega}\right]^{2}} \]

相位为:

\[\theta=\tan^{-1}\left[\frac{-\dot{v}(0)}{\omega v(0)}\right] \]

2.2.3 有阻尼自由振动

如果单自由度体系考虑阻尼,那么根为:

\[s_{1.2}=-\frac c{2m}\pm\sqrt{\left(\frac c{2m}\right)^2-\omega^2}\tag{3} \]

  • 临界阻尼状态

当公式\(\tag{3}\)的根号项为0,即\(\omega=\frac{c}{2m}\).得出临界阻尼系数:\(c_{c}=2m\omega\),此时两根相等:

\[s_1=s_2=-\frac{c_c}{2m}=-\omega \]

体系的位移解为:

\[v(t)=\begin{bmatrix}v(0)(1-\omega t)+\dot{v}(0)t\end{bmatrix}\mathrm{exp}(-\omega t)\tag{4} \]

img

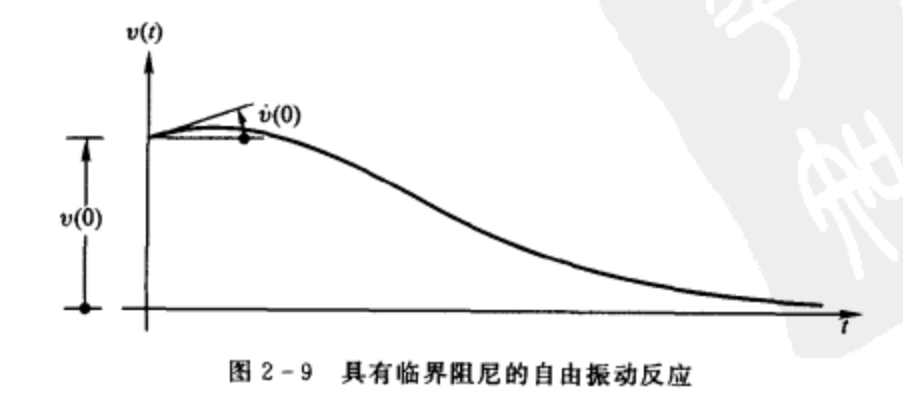
可见,临界阻尼系数C_c给出了自由震动中不出现震荡的最小阻尼值

  • 欠阻尼状态

当体系阻尼值小于临界阻尼,即\(c<c_c=2m\omega\),则公式(3)的根号项小于零.定义阻尼比为:

\[\xi\equiv\frac{c}{c_c}=\frac{c}{2m\omega} \]

此时有:

\[s_{1,2}=-\xi\omega\pm i\omega_D \]

其中,\(\omega_D=\omega\sqrt{1-\xi^2}\)是体系的有阻尼自振频率.可以看出对于常见的结构(阻尼比通常不超过0.2),\(\omega_D>0.9797\omega\).所以一般认为两者近似一致.

欠阻尼的位移解为:

\[v(t)=\biggl[v(0)\cos\omega_{D}t+\biggl(\frac{\dot{v}\left(0\right)+v\left(0\right)\xi\omega}{\omega_{D}}\biggr)\sin\omega_{D}t\biggr]\exp(-\xi\omega t)\tag{5} \]

另一种形式:

\[v(t)=\rho\cos(\omega_Dt+\theta)\exp(-\xi\omega t)\tag{6} \]

\[\rho=\left[v(0)^2+\left(\frac{\dot{\upsilon}\left(0\right)+\upsilon(0)\boldsymbol{\xi\omega}}{\omega_D}\right)^2\right]^{1/2} \]

\[\theta=-\tan^{-1}\left(\frac{\dot{v}\left(0\right)+v\left(0\right)\boldsymbol{\xi}\boldsymbol{\omega}}{\omega_Dv\left(0\right)}\right) \]

img

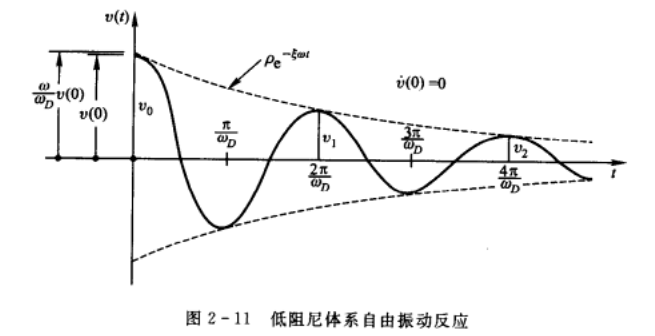
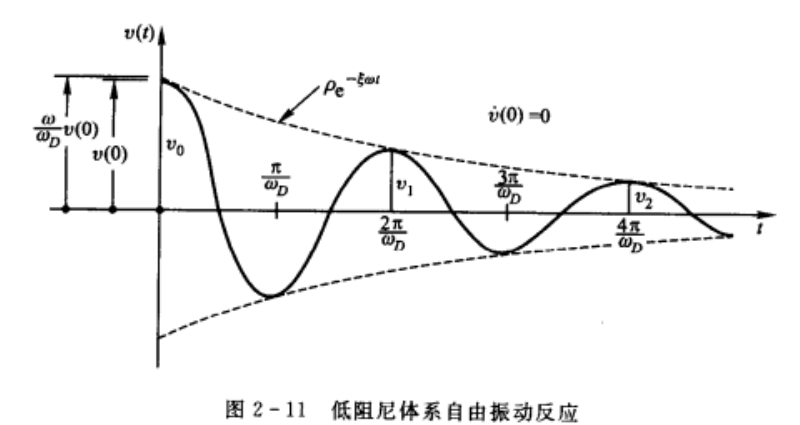
  • 基于自由衰减曲线估算结构阻尼比\(\xi\)和对数衰减率\(\delta\)

典型结构体系的真实阻尼特性是很复杂和难于确定的.因而,通常采用自由振动条件下具有相同衰减率的等效粘滞阻尼比:来表示实际结构的阻尼.为此,需要把图2-11所示的自由振动反应与粘滞阻尼比更充分地联系起来.

img

img

  • 过阻尼状态

过阻尼的结构一般不会遇到.过阻尼状态下,阻尼比大于1,方程的根为:

\[s_{1,2}=-\xi\omega\pm\omega\sqrt{\xi^2-1}=-\xi\omega\pm\hat{\omega} \]

过阻尼情况不会发生震荡,而是类似欠阻尼状态.

2.3 单自由度体系的谐振载荷分析

当单自由度体系受到正弦载荷p(t)时,运动方程为:

\[m\ddot{v}\left(t\right)+c\dot{v}\left(t\right)+kv\left(t\right)=p_0\sin\bar{\omega}t\tag{7} \]

先讨论无阻尼的情况,再讨论有阻尼的解

2.3.1 无阻尼谐振载荷

无阻尼运动方程:

\[m\ddot{v}\left(t\right)+kv\left(t\right)=p_0\sin\bar{\omega}t\tag{8} \]

上式子的补解为:

\[v_c(t)=A\cos\omega t+B\sin\omega t \]

而特解为:

\[v_p(t)=C\sin\overline{\omega}t \]

其中,可以定义\(\beta=\frac{\bar{\omega}}{\omega}\),表示载荷频率与固有自振频率的比值,则有:

\[C=\frac{p_0}k\left[\frac1{1-\beta^2}\right] \]

公式(8)的通解如下,A,B由初始条件\(v(0),\dot{v}(0)\)确定:

\[v(t)=v_{c}(t)+v_{p}(t)=A\cos\omega t+B\sin\omega t+\frac{p_{0}}{k}\biggl[\frac{1}{1-\beta^{2}}\biggr]\sin\overline{\omega}t \]

假设体系由静止开始受到激励,则\(v(0)=0,\dot{v}(0)=0\). A,B为:

\[A=0;B=-\frac{p_0\beta}{k}\biggl[\frac{1}{1-\beta^2}\biggr] \]

在这样的情况下,体系位移为:

\[v(t)=\frac{p_{0}}{k}\biggl[\frac{1}{1-\beta^{2}}\biggr](\sin\bar{\omega}t-\beta\sin\omega t)\tag{9} \]

其中:

  • \(p_0/k=v_{st}\): 载荷p0静止的作用于体系而引发的位移(静位移)
  • \(1/(1-\beta^2)\):谐振荷载放大效应的系数MF

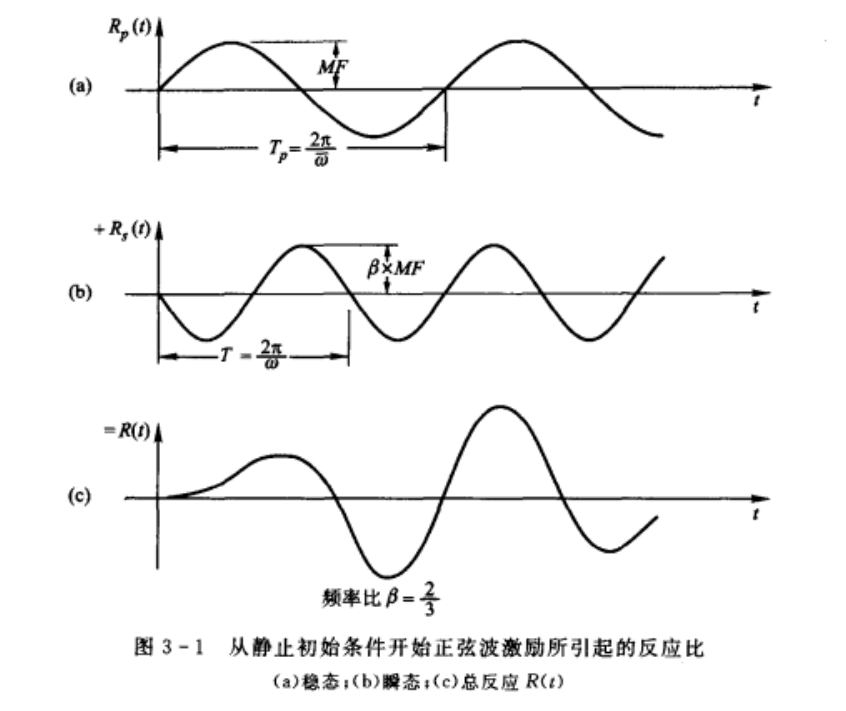
在方程中,\(sin \bar{\omega}t\)是与荷载直接相关并按荷载频率振动的反应分量,称为稳态反应;\(sin \omega t\)是受到反应初始条件控制的、按固有频率振动的自由振动效应分量.在实际情况中,阻尼将使最后一项最终消失,故称该项为瞬态反应.然而,对于这个假想的无阻尼系统,这一项不会衰减掉,而将无限制的持续下去.

通过定义反应比\(R(t)=v(t)/v_{st}\),可以度量动力载荷的影响.公式(9)可以改写为反应比:

\[R(t)=\biggl[\frac{1}{1-\beta^{2}}\biggr](\sin\bar{\omega}t-\beta\sin\omega t) \]

img

2.3.2 有阻尼谐振载荷

现在讨论包含粘滞阻尼的公式(7),变换以下得到:

\[\ddot{v}\left(t\right)+2\xi\omega\dot{v}\left(t\right)+\omega^{2}v\left(t\right)=\frac{p_{0}}{m}\mathrm{sin}\overline{\omega}t\tag{10} \]

其补解是:

\[v_c(t)=\begin{bmatrix}A\mathrm{cos}\omega_Dt+B\mathrm{sin}\omega_Dt\end{bmatrix}\mathrm{exp}(-\xi{\boldsymbol{\omega}t}) \]

特解为:

\[v_p(t)=G_1\cos\bar{\omega}t+G_2\sin\bar{\omega}t \]

其中G1,G2可以根据结构特性和载荷频率计算:

\[G_{1}=\frac{p_{0}}{k}\biggl[\frac{-2\xi\beta}{(1-\beta^{2})^{2}+(2\xi\beta)^{2}}\biggr]\\G_{2}=\frac{p_{0}}{k}\biggl[\frac{1-\beta^{2}}{(1-\beta^{2})^{2}+(2\xi\beta)^{2}}\biggr] \]

结合补解和特解,可以得到方程(10)的通解如下,第一部分表示瞬态反应,第二部分表示稳态反应,在谐振载荷下瞬态反应一般很快就衰减了,工程上更加关心稳态反应:

\[v(t)=(A\cos\omega_{D}t+B\sin\omega_{D}t)\exp(-\xi\omega t)+\frac{p_0}k\biggl[\frac1{(1-\beta^2)^2+(2\xi\beta)^2}\biggr]\biggl[(1-\beta^2)\sin\bar{\omega}t-2\xi\beta\cos\bar{\omega}t\biggr] \]

结构的有阻尼稳态谐振反应特性为:

\[v(t)=\frac{p_0}k\biggl[\frac1{(1-\beta^2)^2+(2\xi\beta)^2}\biggr]\biggl[(1-\beta^2)\sin\bar{\omega}t-2\xi\beta\cos\bar{\omega}t\biggr]\tag{11} \]

经过合成,可以给出三角形式的有阻尼稳态反应特性:

\[v_\rho(t)=\rho\mathrm{sin}(\bar{\omega}t-\theta)\tag{12} \]

其中,振幅为:

\[\rho=\frac{p_0}k[(1-\beta^2)^2+(2\xi\beta)^2]^{-1/2}\tag{13} \]

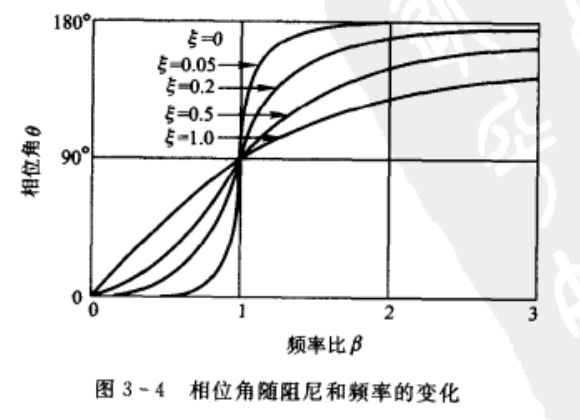
稳态响应滞后于载荷的相位角\(\theta\)(取值范围为0度到180度),为:

\[\theta=\tan^{-1}\left(\frac{2\boldsymbol{\xi}\beta}{1-\beta^2}\right)\tag{14} \]

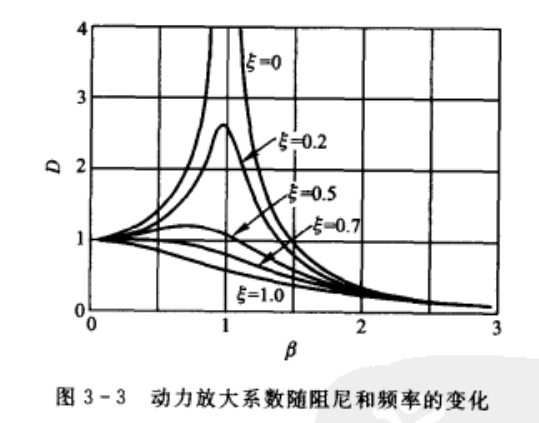
定义动力放大系数D:

\[D\equiv\frac\rho{p_0/k}=[(1-\beta^2)^2+(2\xi\beta)^2]^{-1/2} \]

img

img

2.3.3一般情况的有阻尼谐振载荷

上一节推导了,\(p(t)=p_0 sin(\bar{\omega} t)\)的情况,现在考虑一般情况,即\(p(t)=p_0 e^{[i(\bar{\omega}t+φ)]}\)的情况. 运动方程为:

\[\ddot{v}\left(t\right)+2\xi\omega\dot{v}\left(t\right)+\omega^{2}v\left(t\right)=\frac{p_{0}}{m}\exp\left[i\left(\overline{\omega}t+\phi\right)\right] \]

方程(3-25)的特解及它对时间的一阶、二阶导数为:

\[\begin{aligned}&v_{p}(t)=G\exp(i\bar{\omega}t)\\&\dot{v}_{p}(t)=i\bar{\omega}G\exp(i\bar{\omega}t)\\&\ddot{v}_{p}(t)=-\frac{-2}{\omega}G\exp(i\bar{\omega}t)\end{aligned} \]

其中,G为:

\[G=\frac{p_{0}}{k}\biggl[\frac{1}{(1-\beta^{2})+i(2\xi\beta)}\biggr]=\frac{p_{0}}{k}\biggl[\frac{(1-\beta^{2})-i(2\xi\beta)}{(1-\beta^{2})^{2}+(2\xi\beta)^{2}}\biggr] \]

整理为三角形式的总反应:

\[v_p(t)=\rho exp[i(\bar{\omega}t-\theta)] \]

其中,振幅和相位角与方程(13,14)一致.

2.4 阻尼表征指标及其测量方法

讨论结构响应时,假定结构质量,刚度,阻尼等物理特性已知.在大多数情况下,可以容易的用简单的物理方法或者广义表达式计算出结构的刚度和质量.然而,在实际应用中,结构的基本能量损失机理很难充分了解(即使了解了,也很难用有限元模型表示出来),因此,大多数商业软件会使用等效的阻尼指标来描述与结构的阻尼能力.

事实上，实际的能量损失机理比单自由度运动方程列式时所简单假设的粘滞阻尼力（与速度成正比）要复杂得多。但是，用实验的方法来确定一个适当的粘滞阻尼特性值是可能的。

常用的阻尼表征指标和测量方法:

  • 线性粘滞阻尼(阻尼力和速度成比例):自由衰减法/半功率带宽法等
  • 复刚度阻尼(滞变阻尼--阻尼力与位移成比例)

2.4.1 自由衰减法

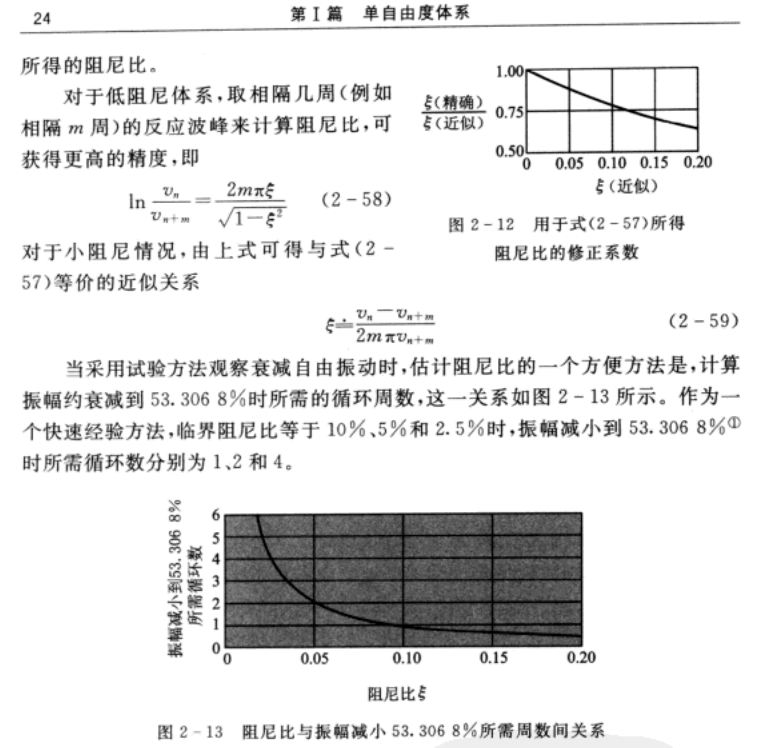
这是一种通过实验测量粘滞阻尼比的最简单、最常用的方法。用任意手段使一个体系产生自由振动后，则可用测量相隔m周的两个位移幅值之比来确定阻尼比。如教材<结构动力学>第2章所示，阻尼比可用如下式子计算：

\[\xi=\frac{\delta_{m}}{2\pi m(\omega/\omega_{D})}\doteq\frac{\delta_{m}}{2\pi m} \]

其中:\(\delta_{m}=ln(v_n/v_{n+m})\)为m周后的对数衰减率;\(\omega\)为自由振动频率,\(\omega_{D}\)为阻尼振动频率

img

  • 优点

简单、直观,设备简单,测量方便

  • 缺点

阻尼比依赖于实验数据;如果阻尼符合线性粘滞阻尼,那么对于任意一组m周循环的结果,计算得到的阻尼比都相同;对于中高阻尼结构不适用,低阻尼结时\(\xi=0.2\)时,计算误差仅有2%

2.4.2 共振放大法

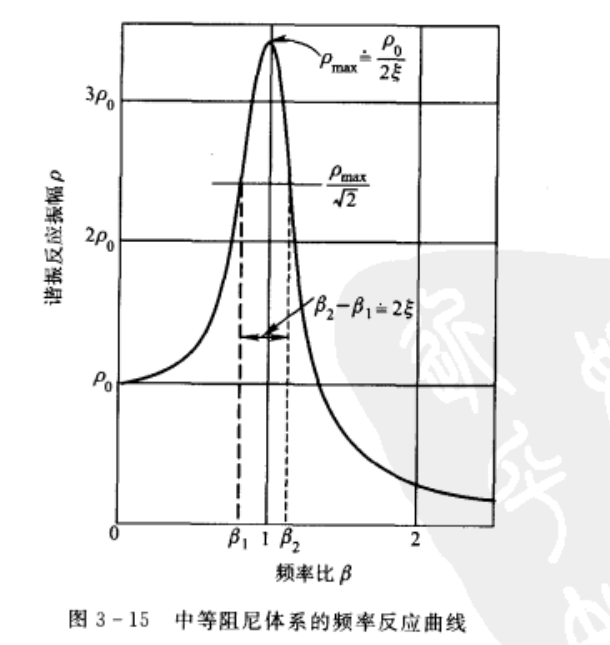
该方法基于相对位移反应的稳态振幅测量,对结构施加谐振载荷,载荷幅值p0,载荷激励频率范围:\([\bar{\omega}-\Delta,\bar{\omega}+\Delta]\),测量出一组结构振幅的数据,得到频率-反应曲线(如下图).

对于低阻尼结构,阻尼比如下式子计算:

\[\xi=\rho_0/2\rho_{max} \]

img

  • 优点

测量简单

  • 缺点

典型的谐振加载无法在0Hz工作,因此静位移\(\rho_0\)很可能出问题;此外计算得到的阻尼比与谐振幅值P0依赖性很大,即\(\xi=f(p0)\),并不十分精准.

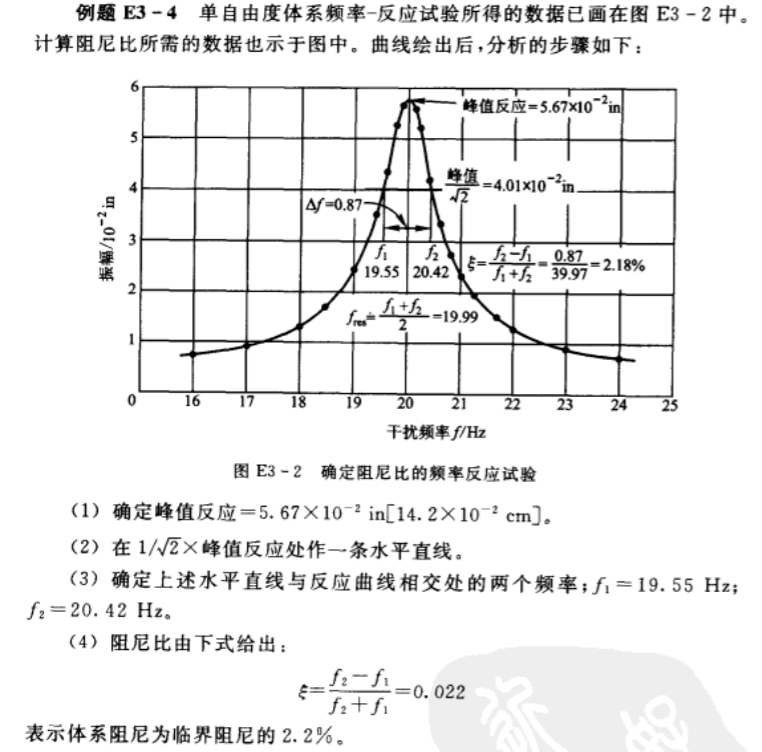
2.4.3 半功率带宽法

同样是利用的实验数据,另一个计算阻尼比的方法是利用半功率带宽法。阻尼比由反应振幅\(\rho\)减小到峰值\(\rho_{max}\)的\(1/sqr(2)\)水平时的频率来确定.公式如下:

\[\xi=\frac{\beta_{2}-\beta_{1}}{\beta_{2}+\beta_{1}}=\frac{f_{2}-f_{1}}{f_{2}+f_{1}} \]

其中f1和f2是反应振幅等于最大振幅乘以1/√2时的频率.

img

2.4.4 每周共振能量损失法

测量复杂,见教材p46

2.4.5 复刚度阻尼的确定

之前的四种方法得到的都是线性粘滞阻尼,这是一种被广泛应用的定义.但具有一个严重缺点: 计算的阻尼比对激励频率的依赖性很大(\(\xi=f(\omega)\)).而大量实验结果表明阻尼力和试验频率几乎无关.

为了消除阻尼力与频率的依赖性,可采用滞变阻尼代替粘滞阻尼,在谐波运动下,滞变阻尼力表示为:

\[f_{D}(t)=i\zeta kv(t) \]

其中,\(\zeta\)是滞变阻尼系数,其他地方一般用\(\eta\)表示.由此定义复刚度\(\hat{k}=k(1+i\xi)\),并且得出单自由度下谐振载荷受迫振动方程:

\[m\ddot{v} (t)+\hat{k}v(t)=p_{0}\exp(i\bar{\omega}t)\tag{15} \]

经过计算,可以得到具有滞变阻尼的稳态反应解:

\[v_{p}(t)=\frac{p_{0}}{k}\biggl[\frac{(1-\beta^{2})-i\zeta}{(1-\beta^{2})^{2}+\zeta^{2}}\biggr]\mathrm{exp}(i\overline{\omega}t)\tag{16} \]

公式(16)写为三角形式:

\[v_{\rho}(t)=\overline{\rho}\exp(i\overline{\omega}t-\overline{\theta})\tag{17} \]

\[\overline{\rho}=\frac{p_{0}}{k}[(1-\beta^{2})^{2}+\zeta^{2} ]^{-1/2} \]

\[\overline{\theta}=\tan^{-1}\left[\frac{\zeta}{(1-\beta^{2})}\right] \]

将上式和公式(13)(14)对比,可以发现:\(\zeta=2\xi\beta\)时,由滞变阻尼引起的稳态反应与粘滞阻尼的相同。

这时稳辐\(\bar{\rho}\)还是想粘滞阻尼一般,依赖于激振频率\(\bar{\omega}\).根据教材P48页推导,可以知道:

\(\zeta=2\xi\)时,复刚度\(\hat{k}=k(1+i2\xi)\),并得到结论:此时的每周能量损失并不具有频率依赖性,处于这个理由,要测量结构阻尼性能,比较推荐使用滞变阻尼(复刚度阻尼)形式表征.

也许这就是为什么DMA测试得到的是损耗因子\(\eta\)而不是阻尼比\(\xi\)的原因.

2.5 多自由度方程体系

以下图的梁结构举例子,说明如何建立多自由度结构的动力学方程.假定这个结构的运动由梁上一系列离散点的位移v1(t),v2(t),……,v_N(t)所确定。原则上，结构的这些点可以任意设置.

img

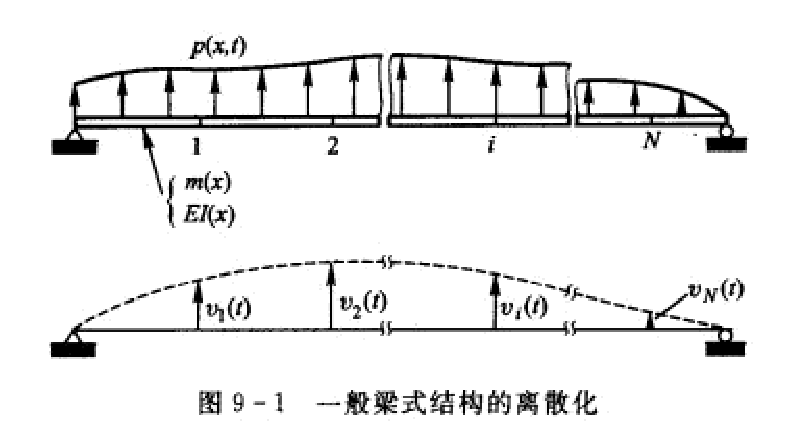
每个自由度至少包含四种作用力:外载荷力/阻尼力/惯性力/弹性力,针对每个自由度都可以列出动力平衡方程:

\[f_{I1}+f_{D1}+f_{S1}=p_{1}\left(t\right)\\f_{I2}+f_{D2}+f_{S2}=p_{2}\left(t\right)\\f_{I3}+f_{D3}+f_{S3}=p_{3}\left(t\right)\\............ \]

写成矩阵形式:

\[f_1+f_D+f_S=p(t)\tag{18} \]

若假定结构行为是线性的,且使用叠加定理,则弹性力向量可以写成:

\[\begin{bmatrix}f_{S1}\\f_{S2}\\\cdots\\f_{S1}\\\cdots\end{bmatrix}=\begin{bmatrix}k_{11}&k_{12}&k_{13}&\cdots&k_{1i}&\cdots&k_{1N}\\k_{21}&k_{22}&k_{23}&\cdots&k_{2i}&\cdots&k_{2N}\\&&\cdots&\cdots&\cdots&\cdots\\k_{11}&k_{i2}&k_{i3}&\cdots&k_{iN}&\cdots&k_{iN}\\&&\cdots&\cdots&\cdots&\cdots&\end{bmatrix}\begin{bmatrix}v_{1}\\v_{2}\\\cdots\\v_{i}\\\cdots\end{bmatrix} \]

其中\(k_{ij}\)为刚度矩阵,\(v_i\)为自由度i的位移.

同理,假定阻尼力与速度有关,则阻尼力向量可以写成:

\[\begin{bmatrix}f_{D1}\\f_{D2}\\...\\f_{D2}\\...\end{bmatrix}=\begin{bmatrix}c_{11}&c_{12}&c_{13}&\cdots&c_{1i}&\cdots&c_{1N}\\c_{21}&c_{22}&c_{23}&\cdots&c_{2i}&\cdots&c_{2N}\\&&...............\\c_{i1}&c_{i2}&c_{i3}&\cdots&c_{ii}&\cdots&c_{iN}\\&&...............\end{bmatrix}\begin{bmatrix}\dot{v}_1\\\\\dot{v}_2\\\\...\\\\\dot{v}_i\\...\end{bmatrix} \]

其中\(c_{ij}\)为阻尼矩阵,\(\dot{v}_i\)为自由度i的速度.

同理,惯性力向量可以写成:

\[\begin{pmatrix}f_{11}\\f_{12}\\...\\f_{1i}\\...\end{pmatrix}=\begin{pmatrix}m_{11}&m_{12}&m_{13}&...&m_{1i}&...&m_{1N}\\m_{21}&m_{22}&m_{23}&...&m_{2i}&...&m_{2N}\\&&...............\\m_{i1}&m_{i2}&m_{i3}&...&m_{ii}&...&m_{iN}\\&&............&&&\end{pmatrix}\begin{pmatrix}\ddot{v}_{1}\\\ddot{v}_{2}\\...\\\ddot{v}_{i}\\...\end{pmatrix} \]

其中\(m_{ij}\)为质量矩阵,\(\ddot{v}_i\)为自由度i的加速度.

完整的动力学方程为:

\[m\ddot{\nu}(t)+c\dot{\nu}(t)+kv(t)=p(t)\tag{19} \]

2.5.1 结构特性矩阵的计算

2.5.1.1 弹性特性矩阵

计算结构的刚度矩阵/柔度矩阵的方法:

  • 实验法:依据刚度矩阵的定义来计算
  • 基于有限单元法:推导单元刚度矩阵,并用直接刚度法进行叠加,得到总刚度矩阵(教材p145)
  • abaqus等商业软件可以导出单元刚度矩阵和全局刚度矩阵.

2.5.1.2 质量特性矩阵

两种方法:

  • 一致质量矩阵
  • 集中质量矩阵

计算方法不在这里详细说明(见教材p147).

2.5.1.3 阻尼特性矩阵

如果作用在结构上各种阻尼力能够定量地确定的话，那么有限单元的概念可以再一次用来确定体系的阻尼系数。例如，任何单元的系数可能具有如下形
式(与教材式(8-18)中的第二个公式比较)：

\[c_{ij}=\int_0^Lc(x)\psi_i(x)\psi_j(x)\mathrm{d}x \]

\(c(x)\) 表示分布的粘滞阻尼特性.单元的阻尼影响系数被确定以后，整个结构的阻尼矩阵就能够应用与直接刚度法相同的叠加过程求得。

然而阻尼特性c(x)(或任何其他特殊的阻尼特性)实际上是算不出来的。因此，常常根据类似结构的实验所确定的阻尼比来表示阻尼，而不用一个明确的阻尼矩阵c。

如果需要一个明确的阻尼矩阵表达式，一般是根据给定阻尼比计算出阻尼矩阵.

2.5.1.4 外载荷特性

载荷特性矩阵是根据给定的集中力,分布力等,计算后得到的N x 1的列向量.

2.5.1.5 几何刚度矩阵

略

2.5.2 多自由度结构的无阻尼自由振动

多自由度的无阻尼自由振动方程:

\[\boldsymbol{m}\boldsymbol{\ddot{\nu}}+\boldsymbol{k}\boldsymbol{\nu}=\boldsymbol{0}\tag{20} \]

2.5.2.1 振动频率分析

与单自由度体系类似,假定多自由度体系的自由振动是简谐运动,位移解写成:

\[v(t)=\hat{v}\sin(\omega t+\theta)\tag{21} \]

其中,\(\hat{v}\) 为自由度振幅向量(表示振型的形状),\(\omega\) 为无阻尼自由振动的频率,\(\theta\) 为相位角.

将公式(21)代入公式(20),得:

\[\begin{bmatrix}k-\omega^2m\end{bmatrix}\hat{\nu}=0\tag{22} \]

上式即为特征是问题或者叫做本征值问题.当满足公式(23)时,多自由度体系表现为有限振幅的自由振动.公式(23)也可以称为体系的频率方程:

\[\parallel k-\omega^2m\parallel=0\tag{23} \]

解出公式(23)的N个根,即为自由振动的N个特征频率.频率向量\(\boldsymbol{\omega}\):

\[\boldsymbol{\omega}=\begin{bmatrix}\omega_1\\\\\omega_2\\\\\omega_3\\\vdots\\\omega_N\end{bmatrix}\tag{24} \]

可以证明: 稳定的结构体系具有实的、对称的、正定的质量和刚度矩阵，频率方程
所有的根都是实的和正的。

2.5.2.2 振型分析

确定特征频率后,第n阶振型,基于运动方程(22)可以写成:

\[\widetilde{E}^{(n)}\hat{v}_{n}=0\tag{25} \]

其中,\(\widetilde{E}^{(n)}=k-\omega_{n}^{2}m\),每个振型下该矩阵不一样.

振动体系的形状可以按照任何一个自由度坐标相对大小的分布来定义。

将N个振动频率\(\omega_i\)代入公式(25),可以得到N个振型向量\(\phi_i\),组成了方阵\(\Phi\):

\[\left.\Phi=(\phi_{1}\quad\phi_{2}\quad\phi_{3}\quad\cdots\quad\phi_{N})=\left[\begin{array}{ccccc}\phi_{11}&\phi_{12}&\cdots&\phi_{1N}\\\phi_{21}&\phi_{22}&\cdots&\phi_{2N}\\\phi_{31}&\phi_{32}&\cdots&\phi_{3N}\\\phi_{41}&\phi_{42}&\cdots&\phi_{4N}\\&\cdots\cdots\cdots\cdots\\\phi_{N1}&\phi_{N2}&\cdots&\phi_{NN}\end{array}\right.\right] \]

振型向量只表示了自由振动的相对形状,因此模态分析的位移结果并无实际的物理意义.

2.5.2.3 振动分析的柔度法

上述振动分析基于运动方程的刚度矩阵，但在许多情形中，用柔度矩阵表示结构的弹性特性比用刚度矩阵更方便。在式(22)前乘\((1/\omega^2)\widetilde{f}\) 就能很容易地将其转化为柔度形式，其中柔度矩阵\(\widetilde{f}\)是刚度矩阵k的逆矩阵，结果为

\[\left[\frac{1}{\omega^{2}}I-\bar{f}m\right]\hat{v}=0\tag{26} \]

其中,\(I\)是N阶单位阵.和之前相同,当满足公式(27)时,上式才有非零解.

\[\left\|\frac1{\omega^2}I-\bar{f}m\right\|=0\tag{27} \]

采用2.5.2.1和2.5.2相同的方法,可以求出特征频率和振型.两种解法唯一的基本差别是方程(27)的根为频率平方的倒数而不是频率平方

2.5.2.4 轴向力的影响

略

2.5.2.5 正交条件

略

2.5.3 多自由度结构的动力反应分析--叠加法

2.5.3.1 正规坐标

针对N自由度的线性体系,位移状态可用N个分量的位移向量\(\boldsymbol{\nu}\),自由振动的振型构成了N个独立的位移模式，其幅值可以作为广义坐标以表示任
意形式的位移。因此，振型起一组Fourier级数中三角函数的作用，它们被应用的原因是：(1)它们具有正交特性；(2)取很少几项就能够有效地描述全部N个位移。

例如，考虑图12-1所示的悬臂柱，其挠度曲线用三个水平的平移坐标确定。

如图所示，此结构任何位移向量\(\boldsymbol{\nu}\)都可通过叠加模态振型
求得。即\(v_{s}=\phi_{s}Y_{s}\)

img

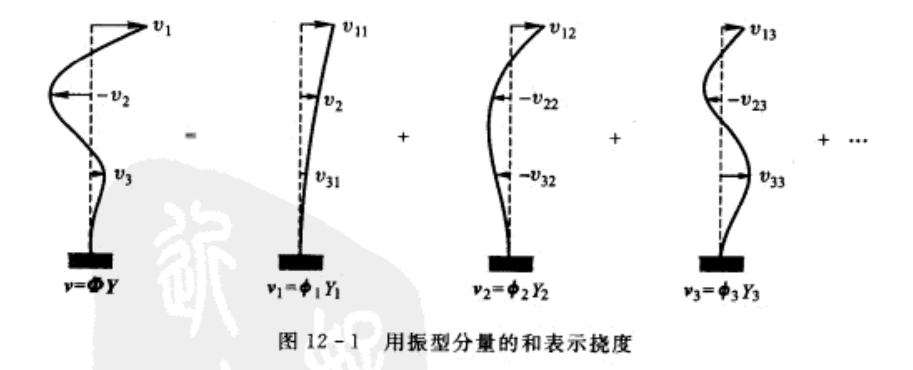
\[v=\phi_{1}Y_{1}+\phi_{2}Y_{2}+\cdots+\phi_{N}Y_{N}=\sum_{n=1}^{N}\phi_{n}Y_{n} \]

矩阵形式:

\[v=\Phi Y\tag{28} \]

其中,\(\Phi\) 为N x N振型矩阵,每一列都代表一个模态振型,\(Y\) 为结构的正规坐标,有N个分量,\(\phi_n\)为第n个振型向量.

正规坐标向量根据下式计算(m为质量矩阵):

\[Y_{n}=\frac{\boldsymbol{\phi}_{n}^{\mathrm{T}}m\nu}{\boldsymbol{\phi}_{n}^{\mathrm{T}}m\boldsymbol{\phi}_{n}}\quad n=1,2,\cdots,N\tag{29} \]

如果位移向量\(\boldsymbol{\nu}\)随时间变化,则正规坐标向量也随时间变化:

\[\dot{Y}_{n}(t)=\frac{\boldsymbol{\phi}_{n}^{\mathrm{T}}m \dot{\nu}(t)}{\boldsymbol{\phi}_{n}^{\mathrm{T}}m\Phi_{n}}\tag{30} \]

\[\ddot{Y}_{n}(t)=\frac{\boldsymbol{\phi}_{n}^{\mathrm{T}}m \ddot{\nu}(t)}{\boldsymbol{\phi}_{n}^{\mathrm{T}}m\Phi_{n}}\tag{31} \]

2.5.3.2 非耦合的运动方程：无阻尼

用正规振型的正交特性来简化多自由度体系的运动方程。

多自由度-无阻尼体系的运动方程:

\[m \ddot{\nu} (t)+kv(t)=p(t)\tag{32} \]

带入正规坐标后:

\[m\Phi\ddot{Y}(t)+k\Phi Y(t)=p(t) \]

根据振型正交性可以得到:

\[\phi_{n}^{\mathrm{T}}m\phi_{n}\ddot{Y}_{n}(t)+\phi_{n}^{\mathrm{T}}k\phi_{n}Y_{n}(t)=\phi_{n}^{\mathrm{T}}p(t) \]

此时可以定义新变量:

\[M_{n}\equiv\phi_{n}^{\mathrm{T}}m\phi_{n}\quad K_{n}\equiv\phi_{n}^{\mathrm{T}}k\phi_{n} \quad P_{_n}(t)\equiv\phi_{_n}^{\dagger}p\left(t\right)\tag{33} \]

分别是第n振型的正规坐标广义质量、广义刚度和广义荷载,因此,第n个振型的单自由度运动方程为:

\[M_{n}\ddot{Y}_{n}(t)+K_{n}Y_{n}(t)=P_{n}(t)\tag{34} \]

其中广义刚度与广义质量的关系:

\[K_{n}=\omega_{n}^{2}M_{n},\omega_{n}是n阶振型对应的特征频率\tag{35} \]

对于无阻尼结构的每一个振型，可以用上述方法求得一个独立的单自由度运动方程。因此，采用正规坐标，就可以将由于质量与刚度矩阵中非对角项而耦合的、N个联立的运动微分方程，转换成为N个独立的正规坐标方程。由此，确定动力反应时，首先分别求解每一个正规（振型）坐标的反应，然后按式(28)叠加即可得出用原始几何坐标表示的反应。这种方法叫做振型叠加法，或者更确切地说叫做振型位移叠加法。

2.5.3.3 非耦合的运动方程：粘滞阻尼

现在可用正规振型的正交特性来简化多自由度体系的有阻尼-运动方程。

多自由度-有阻尼体系的运动方程:

\[m \ddot{v} (t)+c v (t)+kv(t)=p(t)\tag{36} \]

带入正规坐标后:

\[\phi_{n}^{\mathrm{T}}m\Phi\ddot{Y}\left(t\right)+\phi_{n}^{\mathrm{T}}c\Phi\dot{Y}\left(t\right)+\phi_{n}^{\mathrm{T}}k\Phi Y\left(t\right)=\phi_{n}^{\mathrm{T}}p\left(t\right) \]

假设振型正交性也适用于阻尼矩阵,即\(\phi_{m}^{\intercal}c\phi_{n}=0\quad m\neq n\); 因此,第n个振型的单自由度运动方程为:

\[M_{n}\ddot{Y}_{n}(t)+C_{n}\dot{Y}_{n}(t)+K_{n}Y_{n}(t)=P_{n}(t)\tag{37} \]

其中,\(C_{n}\)定义为广义粘滞阻尼系数(N x 1向量),\(C_n=\phi_n^Tc\phi_n\).

方程(37)的另一种形式:

\[\ddot{Y}_{n}(t)+2\xi_{n}\omega_{n} \dot{Y}_{n}(t)+\omega_{n}^{2}Y_{n}(t)=\frac{P_{n}(t)}{M_{n}} \]

以上中,N阶模态振型的粘滞阻尼比,定义为:

\[\xi_n=\frac{C_n}{2\omega_nM_n}\tag{38} \]

前面已经指出，用每一个振型的阻尼比来确定多自由度体系的阻尼，比求阻尼矩阵c的系数要方便得多，且从物理意义上说也更合理。因为，在大多数情况下振型阻尼比ξ，可以通过实验来确定，或者有足够精确的估计。

2.5.3.4 用振型位移叠加法进行反应分析

叠加法是一种求解多自由度动力系统的有效方法。

  • 粘滞阻尼表示阻尼时

同2.5.3.3节,使用正规矩阵讲N自由度体系的有阻尼运动方程转换为N个非耦合的单自由度运动方程:

\[\ddot{Y}_{n}(t)+2\xi_{n}\omega_{n}\dot{Y}_{n}(t)+\omega_{n}^{2}Y_{n}(t)=\frac{P_{n}(t)}{M_{n}}\quad n=1,2,\cdots,N \]

求解第一步,求解特征值问题:

\[\begin{bmatrix}k-\omega^2m\end{bmatrix}\hat{\nu}=0 \]

从而确定振型\(\phi_n(n=1,2,\cdots)\text{和相应的频率}\omega_n.\)振型阻尼比一般需要手动假定，或者通过实验来确定。

求解第二步,计算N个非耦合的单自由度运动方程的解\(Y(t)\)(推导过程详见教材p177),假定结构处于0初始状态,即$ Y_{n}=\dot{Y}=0\(,则\)t>=0$时的振型反应为求解如下方程:

\[Y_{n}(t) = \frac{1}{M_{n}\omega_{n}} \int_{0}^{t}P_{n}(\tau)\exp\Bigl[-\xi_{n}\omega_{n}(t-\tau)\Bigr]\sin \omega_{Dn}(t-\tau) \mathrm{d}\tau \]

求解第三步,计算得到每一振型的反应\(Y_n(t)\),则位移向量\(\nu(t)\)为:

\[v(t)=\phi_{1}Y_{1}(t)+\phi_{2}Y_{2}(t)+\cdots+\phi_{N}Y_{N}(t)\tag{39} \]

这就是叠加法的基本思路.对于大多数载荷类型,低阶振型的贡献是最大的,实际分析中,一般只考虑低阶振型的位移.不必要计算高阶振型

  • 复刚度阻尼表示阻尼时

其他知识

  • 欧拉方程

img

posted @ 2024-06-19 11:58  FE-有限元鹰  阅读(84)  评论(0)  编辑  收藏  举报