各向异性材料的弹性力学基础
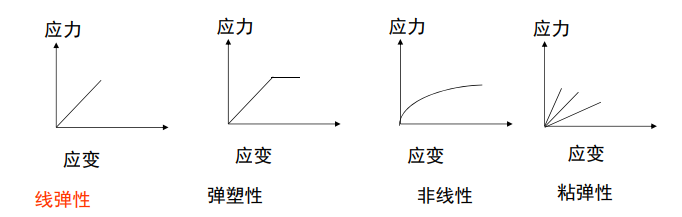
复合材料宏观力学分析的基本假设: 1.所研究的各向异性弹性体为均质连续固体 2.线弹性范围内,服从广义虎克定律.3.小变形
各向异性与各向同性弹性力学的基本方程的差别在于:本构方程.其它平衡方程,几何方程,协调方程,和边界条件等则完全相同
1.弹性力学中的几个基本概念
\[F=\lim_{\Delta V\to0}\frac{\Delta Q}{\Delta V}\\
F=X\boldsymbol{i}+Y\boldsymbol{j}+Z\boldsymbol{k}
\]
\[F=\lim_{\Delta S\to0}\frac{\Delta Q}{\Delta S}\\\boldsymbol{F}=\overline{X}\boldsymbol{i}+\overline{Y}\boldsymbol{j}+\overline{Z}\boldsymbol{k}
\]
\[s=\lim_{\Delta A\to0}\frac{\Delta Q}{\Delta A}
\]
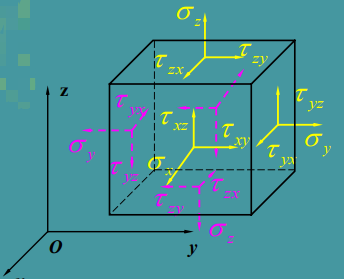
应力:由外力引起的在 P点的某一面上内力分布集度.应力的法向分量为正应力;切向分量为剪应力.
一点应力状态: 通过一点P 的各个面上应力状况的集合.矩阵表示为:
\[[\sigma]=\begin{bmatrix}\sigma_x&\tau_{xy}&\tau_{xz}\\\tau_{yx}&\sigma_y&\tau_{yz}\\\tau_{zx}&\tau_{zy}&\sigma_z\end{bmatrix}
\]
应力符号的意义:
对于正应力:第1个下标表示应力所在面的法线方向;
对于切应力(以\(\tau_{xy}\) 为例):第1个下标表示切应力所在面的法线方向,第2个下标表示切应力的方向.
应力正负号的规定:
正应力:拉为正,压为负.
剪应力:
坐标正面上,与坐标正向一致时为正;
坐标负面上,与坐标正向相反时为正.
根据剪应力互等定理,可以知道:应力矩阵只有6个独立变量:\(\sigma_x,\sigma_y,\sigma_z,\tau_{xy},\tau_{yz},\tau_{xz}\) .
\[\left.\left\{\begin{array}{c}\tau_{xy}=\tau_{yx}\\\tau_{yz}=\tau_{zy}\\\tau_{zx}=\tau_{xz}\end{array}\right.\right.
\]
位移:物体变形时各点位置的改变量称为位移.总位移=刚体位移+形变位移.通常一点P的位移,用它在x、y、z轴上的位移分量u、v、w来表示,以沿坐标轴正向为正,沿坐标轴负向为负 .
\[\overrightarrow{x}^{2}=u\overrightarrow{i}+v\overrightarrow{j}+w\overrightarrow{k}
\]
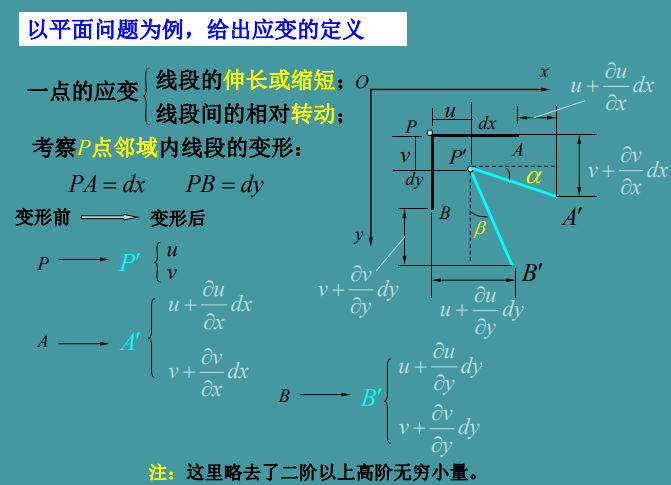
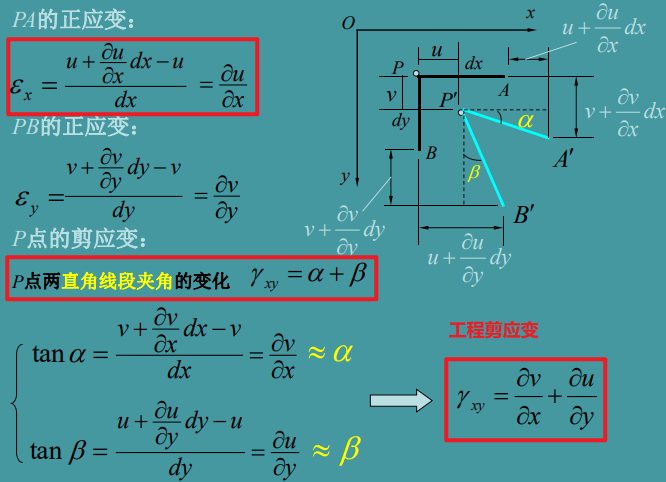
对于三维空间,应变分量可以表示为:
\[\begin{aligned}&\varepsilon_{x}=\frac{\partial u}{\partial x},\varepsilon_{y}=\frac{\partial\nu}{\partial y},\varepsilon_{z}=\frac{\partial w}{\partial z}\\&\gamma_{yz}=\frac{\partial w}{\partial y}+\frac{\partial\nu}{\partial z},\gamma_{zx}=\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x},\gamma_{xy}=\frac{\partial\nu}{\partial x}+\frac{\partial u}{\partial y}\end{aligned}
\]
定义张量应变如下.张量应变和工程应变的关系:正应变两者一致,张量剪应变为工程剪应变的0.5倍.
\[\begin{aligned}\varepsilon_{ij}&=\frac{1}{2}(u_{i,j}+u_{j,i})\quad 其中(i,j&=1,2,3)\end{aligned}
\]
张量应变矩阵为:
\[\begin{bmatrix}\varepsilon\end{bmatrix}=\begin{bmatrix}\varepsilon_x&\gamma_{xy}&\gamma_{xz}\\\gamma_{yx}&\varepsilon_y&\gamma_{yz}\\\gamma_{zx}&\gamma_{zy}&\varepsilon_z\end{bmatrix}\\
\text{其中}\begin{cases}&\gamma_{xy}=\gamma_{yx}\\&\gamma_{yz}=\gamma_{zy}\\&\gamma_{zx}=\gamma_{xz}\end{cases}
\]
2.各向异性弹性力学的基本方程
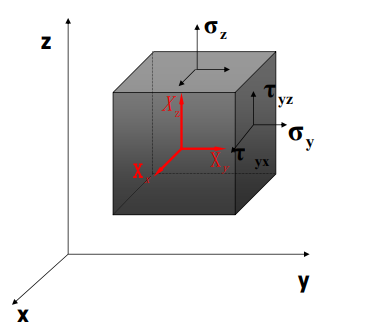
弹性力学平衡方程(equilibrium eqs.):描述应力-位移之间的关系
取一个微元体dx * dy * dz, 假设受到体力\(F=X_x\boldsymbol{i}+X_y\boldsymbol{j}+X_z\boldsymbol{k}\) 的作用, 则有:
\[\frac{\partial\sigma_{x}}{\partial x}+\frac{\partial\tau_{yx}}{\partial y}+\frac{\partial\tau_{zx}}{\partial z}+X_{x}=\rho\frac{\partial^{2}u}{\partial t^{2}}\\
\frac{\partial\tau_{xy}}{\partial x}+\frac{\partial\sigma_{y}}{\partial y}+\frac{\partial\tau_{zy}}{\partial z}+X_{y}=\rho\frac{\partial^{2}\nu}{\partial t^{2}}\\
\frac{\partial\tau_{xz}}{\partial x}+\frac{\partial\tau_{yz}}{\partial y}+\frac{\partial\sigma_{z}}{\partial z}+X_{z}=\rho\frac{\partial^{2}w}{\partial t^{2}}
\]
其中, \(\rho\) 为体积密度,\(X_{x},X_{y},X_{z}\) 为体力密度(unit:N/m^3),\(\sigma_{x},\sigma_{y},\sigma_{z}\) 为应力,\(\tau_{xy},\tau_{xz},\tau_{yz}\) 为张量应变,\(u,\nu,w\) 为位移.
描述应变-位移之间的关系可以用变形协调方程(deformation eqs.)或几何方程(geometry eqs.)表示,两者等效.
三个独立的位移场即可以完全确定变形,而应变亦可以描述变形,它们之间满足以下关系!
\[\varepsilon_{x}=\frac{\partial u}{\partial x}\\
\varepsilon_{y}=\frac{\partial\nu}{\partial y}\\
\varepsilon_{z}=\frac{\partial w}{\partial z}\\
\gamma_{zy}=\frac{\partial w}{\partial y}+\frac{\partial\nu}{\partial z}\\
\gamma_{zx}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}\\
\gamma_{yx}=\frac{\partial u}{\partial y}+\frac{\partial\nu}{\partial x}
\]
\[\frac{\partial^{2}\varepsilon_{x}}{\partial y^{2}}+\frac{\partial^{2}\varepsilon_{y}}{\partial x^{2}}=\frac{\partial^{2}\gamma_{xy}}
{\partial x\partial y}\\
\frac{\partial^{2}\varepsilon_{z}}{\partial x^{2}}+\frac{\partial^{2}\varepsilon_{x}}{\partial z^{2}}=\frac{\partial^{2}\gamma_{zx}}{\partial z\partial x}\\
\frac{\partial^{2}\varepsilon_{y}}{\partial z^{2}}+\frac{\partial^{2}\varepsilon_{z}}{\partial y^{2}}=\frac{\partial^{2}\gamma_{zy}}{\partial z\partial y}\\
\frac{\partial}{\partial x}(\frac{\partial\gamma_{xz}}{\partial y}+\frac{\partial\gamma_{xy}}{\partial z}-\frac{\partial\gamma_{yz}}{\partial x})=2\frac{\partial^{2}\varepsilon_{x}}{\partial z\partial y}\\
\frac{\partial}{\partial y}(\frac{\partial\gamma_{xy}}{\partial z}+\frac{\partial\gamma_{zy}}{\partial x}-\frac{\partial\gamma_{xz}}{\partial y})=2\frac{\partial^{2}\varepsilon_{y}}{\partial z\partial x}\\
\frac{\partial}{\partial z}(\frac{\partial\gamma_{zy}}{\partial x}+\frac{\partial\gamma_{zx}}{\partial y}-\frac{\partial\gamma_{xy}}{\partial z})=2\frac{\partial^{2}\varepsilon_{z}}{\partial y\partial x}
\]
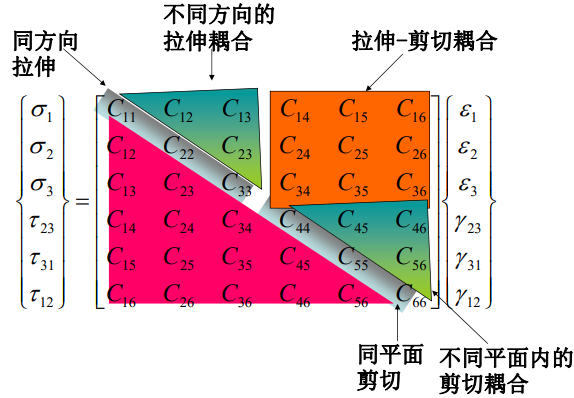
本构方程(constitutive eqs.):描述应力-应变之间的关系
本构方程反映了材料的性质.一般刚度矩阵表示应力应变关系, 它是各向异性弹性力学的基本方程.根据不同材料,矩阵独立变量个数也不同.
\[\begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\tau_{23}\\\tau_{31}\\\tau_{12}\end{bmatrix}=\begin{bmatrix}C_{11}&C_{12}&C_{13}&C_{14}&C_{15}&C_{16}\\C_{21}&C_{22}&C_{23}&C_{24}&C_{25}&C_{26}\\C_{31}&C_{32}&C_{33}&C_{34}&C_{35}&C_{36}\\C_{41}&C_{42}&C_{43}&C_{44}&C_{45}&C_{46}\\C_{51}&C_{52}&C_{53}&C_{54}&C_{55}&C_{56}\\C_{61}&C_{62}&C_{63}&C_{64}&C_{65}&C_{66}\end{bmatrix}\begin{bmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\gamma_{23}\\\gamma_{31}\\\gamma_{12}\end{bmatrix}
\]
综上,
3个位移分量,u,v,w
6个应变分量,\(\varepsilon_\mathrm{x},\varepsilon_\mathrm{y},\varepsilon_\mathrm{z},\gamma_\mathrm{yz},\gamma_\mathrm{xz},\gamma_\mathrm{yx}\)
6个应力分量,\(\sigma_\mathrm{x},\sigma_\mathrm{y},\sigma_\mathrm{z},\tau_\mathrm{yz},\tau_\mathrm{xz},\tau_\mathrm{yx}\)
对应的方程也是15个,静力平衡方程(3)+几何关系(6)+本构方程(6)
定解还需边界条件:
\[\begin{aligned}&\text{给定力的边界条件(3)}\\&\begin{cases}\sigma_xl+\tau_{xy}m+\tau_{xz}n=\overline{X},\text{已知}\\\tau_{yx}l+\sigma_ym+\tau_{yz}n=\overline{Y},\text{已知}\\\tau_{zx}l+\tau_{zy}m+\sigma_zn=\overline{Z},\text{已知}\end{cases}\\&\text{给定位移的边界条件(3)}\\&\begin{cases}u=\overline{u},\text{已知}\\\nu=\overline{\nu},\text{已知}\\w=\overline{w},\text{已知}\end{cases}\end{aligned}
\]
3.各向异性弹性力学的本构方程
在满足线弹性-小变形时,各向异性弹性力学的本构方程可以写成:
\[\sigma_i=C_{ij}\varepsilon_j\quad
\varepsilon_i=S_{ij}\sigma_j\\
其中i,j=1,2,3,4,5,6\\
S=C^{-1}
\]
应力应变本来是张量,将其转换成列阵形式,有:
\[[\sigma]=[\sigma_1, \sigma_2, \sigma_3, \tau_{23}, \tau_{31}, \tau_{12}]=[\sigma_1, \sigma_2, \sigma_3, \tau_{4}, \tau_{5}, \tau_{6}]\\
[\varepsilon]=[\varepsilon_1, \varepsilon_2, \varepsilon_3, \gamma_{23}, \gamma_{31}, \gamma_{12}]=[\varepsilon_1, \varepsilon_2, \varepsilon_3, \gamma_{4}, \gamma_{5}, \gamma_{6}]
\]
注意:这个notation 和abaqus 不一致.
\[\begin{bmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\varepsilon_4\\\varepsilon_5\\\varepsilon_6\end{bmatrix}=\begin{bmatrix}S_{11}&S_{12}&S_{13}&S_{14}&S_{15}&S_{16}\\S_{21}&S_{22}&S_{23}&S_{24}&S_{25}&S_{26}\\S_{31}&S_{32}&S_{33}&S_{34}&S_{35}&S_{36}\\S_{41}&S_{42}&S_{43}&S_{44}&S_{45}&S_{46}\\S_{51}&S_{52}&S_{53}&S_{54}&S_{55}&S_{56}\\S_{61}&S_{62}&S_{63}&S_{64}&S_{65}&S_{66}\end{bmatrix}\begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\sigma_4\\\sigma_5\\\sigma_6\end{bmatrix}
\]
刚度矩阵和柔度矩阵都具有对称性 :\(C_{\begin{array}{c}ij\\\end{array}}=\begin{array}{c}C_{\begin{array}{c}ji\\\end{array}}\end{array}\)
4.几种各向异性弹性力学的本构方程
在均质弹性体中,若过每一点沿不同的方向都具有不同的弹性特性时,这种弹性体称之为一般各向异性体
\[\begin{gathered}\begin{pmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\sigma_4\\\sigma_5\\\sigma_6\end{pmatrix}=\begin{bmatrix}C_{11}&C_{12}&C_{13}&C_{14}&C_{15}&C_{16}\\C_{21}&C_{22}&C_{23}&C_{24}&C_{25}&C_{26}\\C_{31}&C_{32}&C_{33}&C_{34}&C_{35}&C_{36}\\C_{41}&C_{42}&C_{43}&C_{44}&C_{45}&C_{46}\\C_{51}&C_{52}&C_{53}&C_{54}&C_{55}&C_{56}\\C_{61}&C_{62}&C_{63}&C_{64}&C_{65}&C_{66}\end{bmatrix}\begin{bmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\varepsilon_4\\\varepsilon_5\\\varepsilon_6\end{bmatrix}\end{gathered}
\]
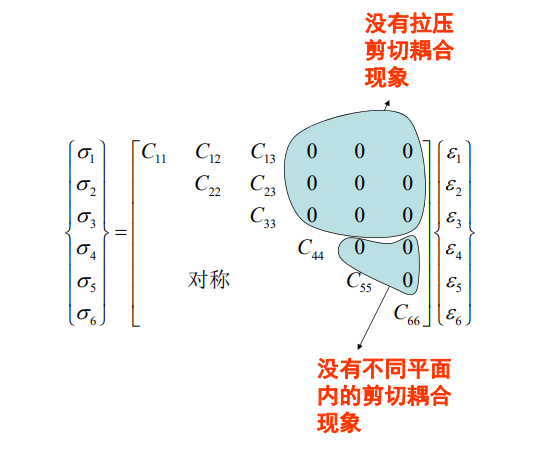
如果材料有两个正交的材料性能对称面,则对于和这两个平面相垂直的第三个平面也具有对称性,这种材材料主向:是指和三个正交对称平面的交线相平行的方向 ;正应力与剪应变之间没有耦合,剪应力与正应变之间没有耦合不同平面内的剪应力和剪应变之间也没有相互作用
\[\begin{bmatrix}\mathbf{\sigma}_1\\\mathbf{\sigma}_2\\\mathbf{\sigma}_3\\\mathbf{\tau}_{23}\\\mathbf{\tau}_{31}\\\mathbf{\tau}_{12}\end{bmatrix}=\begin{bmatrix}\mathbf{C}_{11}&\mathbf{C}_{12}&\mathbf{C}_{13}&\mathbf{0}&\mathbf{0}&\mathbf{0}\\\mathbf{C}_{21}&\mathbf{C}_{22}&\mathbf{C}_{23}&\mathbf{0}&\mathbf{0}&\mathbf{0}\\\mathbf{C}_{31}&\mathbf{C}_{23}&\mathbf{C}_{33}&\mathbf{0}&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{C}_{44}&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{C}_{55}&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{C}_{66}\end{bmatrix}\begin{bmatrix}\mathbf{\varepsilon}_1\\\mathbf{\varepsilon}_2\\\mathbf{\varepsilon}_3\\\mathbf{\gamma}_{23}\\\mathbf{\gamma}_{31}\\\mathbf{\gamma}_{12}\end{bmatrix}
\]
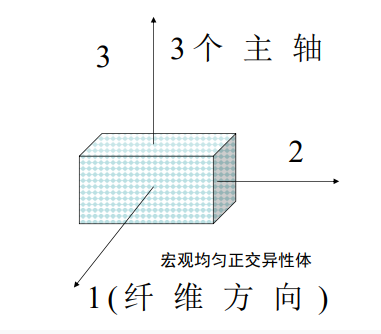
通过分析几何的对称性可推测弹性对称性.例子:纤维在横截面内按距形排列的单向纤维复合材料,宏观而言是一正交异性体的例子.
横观各向同性材料(transverse isotropic materials)
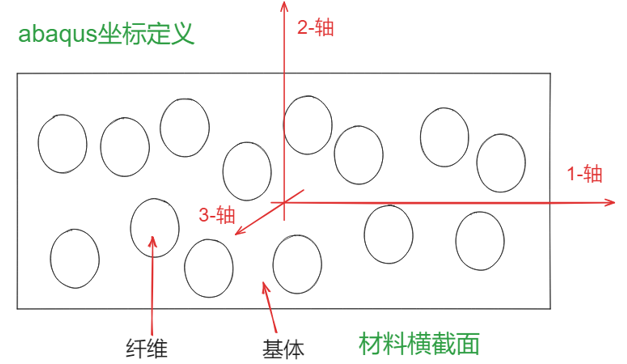
如果材料具有三个互相垂直的弹性性能对称平面,且其 中的一个平面是各向同性的,那么为横观各向同性材料,5个独立常数 .如果通过均质弹性体的每一点都可以找到某一相互平行的平面,并且该平面内所有各个方向的弹性性质均相同.
纤维增强复合材料中:纤维在横截面内是随机排列的,宏观而言,其所有横方向的弹性性能均相同.
当取1-2面为各向同性面时( 下标1,2可以互换,即\(C_{11}=C_{22},C_{44}=C_{55},C_{23}=C_{13}\) ),并且1-2平面旋转任何角度,应变能密度不变,即有:\(C_{66}=\frac{C_{11}-C_{12}}2\) .其刚度矩阵和柔度矩阵格式如下:
这也是abaqus 中使用的notation.
\[\begin{bmatrix}\mathbf{\sigma}_1\\\mathbf{\sigma}_2\\\mathbf{\sigma}_3\\\mathbf{\tau}_{23}\\\mathbf{\tau}_{31}\\\mathbf{\tau}_{12}\end{bmatrix}=\begin{bmatrix}\mathbf{C}_{11}&\mathbf{C}_{12}&\mathbf{C}_{13}&\mathbf{0}&\mathbf{0}&\mathbf{0}\\\mathbf{C}_{12}&\mathbf{C}_{11}&\mathbf{C}_{13}&\mathbf{0}&\mathbf{0}&\mathbf{0}\\\mathbf{C}_{13}&\mathbf{C}_{13}&\mathbf{C}_{33}&\mathbf{0}&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{C}_{44}&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{C}_{44}&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{0}&\mathbf{\frac{C_{11}-C_{12}}{2}}\end{bmatrix}\begin{bmatrix}\mathbf{\varepsilon}_1\\\mathbf{\varepsilon}_2\\\mathbf{\varepsilon}_3\\\mathbf{\gamma}_{23}\\\mathbf{\gamma}_{31}\\\mathbf{\gamma}_{12}\end{bmatrix}
\]
对应的柔度矩阵为:
\[\begin{bmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\gamma_{23}\\\gamma_{31}\\\gamma_{12}\end{bmatrix}=\begin{bmatrix}S_{11}&S_{12}&S_{13}&0&0&0\\S_{12}&S_{11}&S_{13}&0&0&0\\S_{13}&S_{13}&S_{33}&0&0&0\\0&0&0&S_{44}&0&0\\0&0&0&0&S_{44}&0\\0&0&0&0&0&2(S_{11}-S_{12})\end{bmatrix}\begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\tau_{23}\\\tau_{31}\\\tau_{12}\end{bmatrix}
\]
如果材料具有无穷多个性能对称面,它称为各向同性的材料,有2个独立常数
\[\begin{aligned}
&\begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\tau_{23}\\\tau_{31}\\\tau_{12}\end{bmatrix} =\begin{bmatrix}\mathbf{C}_{11}&\mathbf{C}_{12}&\mathbf{C}_{12}&0&0&0\\\mathbf{C}_{12}&\mathbf{C}_{11}&\mathbf{C}_{12}&0&0&0\\\mathbf{C}_{12}&\mathbf{C}_{12}&\mathbf{C}_{11}&0&0&0\\0&0&0&\frac{\mathbf{C}_{11}-\mathbf{C}_{12}}{2}&0&0\\0&0&0&0&\frac{\mathbf{C}_{11}-\mathbf{C}_{12}}{2}&0\\0&0&0&0&0&\frac{\mathbf{C}_{11}-\mathbf{C}_{12}}{2}\end{bmatrix}\begin{bmatrix}\mathbf{\varepsilon}_1\\\mathbf{\varepsilon}_2\\\mathbf{\varepsilon}_3\\\mathbf{\gamma}_{23}\\\mathbf{\gamma}_{31}\\\mathbf{\gamma}_{12}\end{bmatrix}\\
&C_{11} =\mathbf{C}_{22}=\mathbf{C}_{33} \\
&C_{12} =\mathbf{C}_{23}=\mathbf{C}_{31} \\
&C_{44} =\mathbf{C}_{55}=\mathbf{C}_{66}=(\mathbf{C}_{11}-\mathbf{C}_{12})/2
\end{aligned}\]
柔度矩阵为:
\[\begin{bmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\gamma_{23}\\\gamma_{31}\\\gamma_{12}\end{bmatrix}=\begin{bmatrix}S_{11}&S_{12}&S_{12}&0&0&0\\S_{12}&S_{11}&S_{12}&0&0&0\\S_{12}&S_{12}&S_{11}&0&0&0\\0&0&0&2(S_{11}-S_{12})&0&0\\0&0&0&0&2(S_{11}-S_{12})&0\\0&0&0&0&0&2(S_{11}-S_{12})\end{bmatrix}\begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\tau_{23}\\\tau_{31}\\\tau_{12}\end{bmatrix}
\]
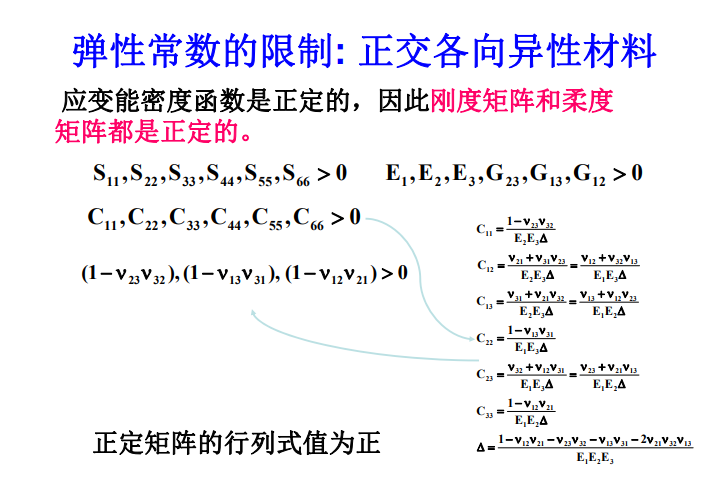
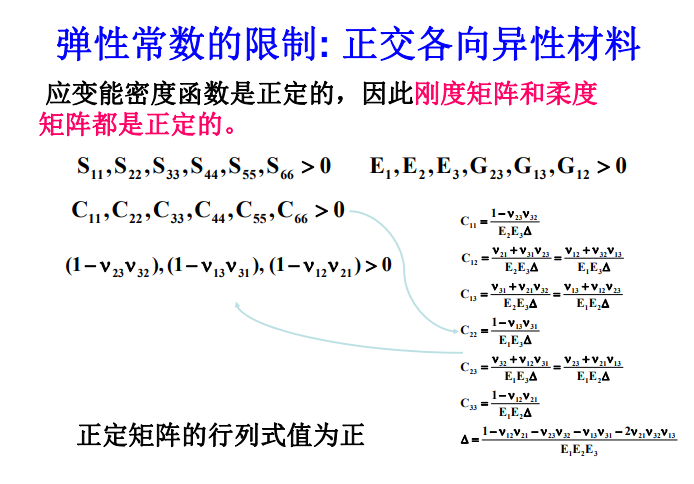
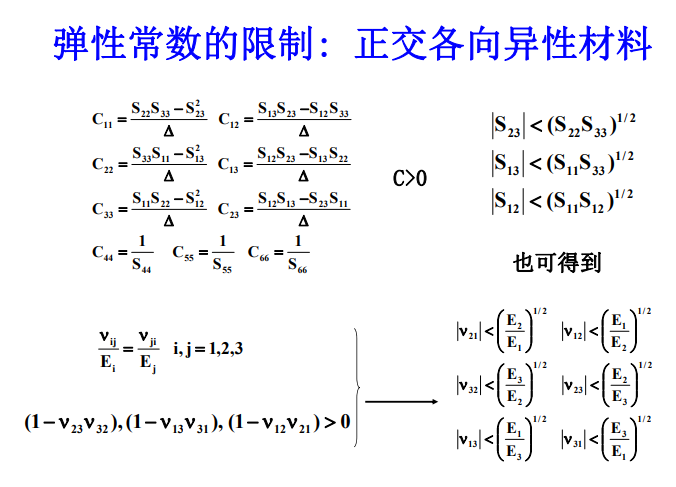
5.正交各向异性材料的工程常数
根据非0应变状态的弹性应变能为正值,应变能应是应变或者是应力的正定二次型 .应变能的表达式为: \(W=\frac12S_{ij}\sigma_i\sigma_j\) ,因此:W是 \(\sigma_{i}\) 的正定二次型的充要条件是矩阵[S]的所有主要主子式大于零 .
6. 单层板宏观力学分析
单层板可以认为是"纤维布"或"预浸料".对单层板作以下假定:
为正交各向异性材料,或者横观各向同性材料.
单向板的厚度尺寸远小于其它两个方向的尺寸
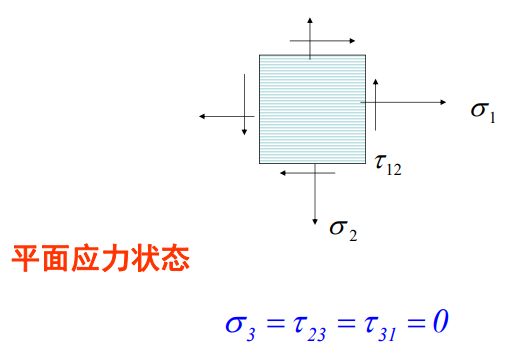
面外应力分量与面内应力分量相比很小,可以忽略,因此单层板问题可以视为二维平面应力问题
线弹性,小变形
连续性
纤维复合材料在纤维方向承受载荷,纤维是主要承载相,基体的作用是支撑纤维保持一定的状态,保护纤维不受损伤并在纤维的端头附近以剪切形式传递载荷.
当在纤维方向以外承受横向载荷时,纤维与基体均同时承担.
均匀性
纤维在基体中基本相互平行,但是在垂直于纤维的方向是随机分布的
不同的弹性模型:
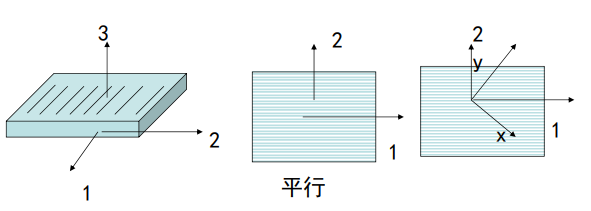
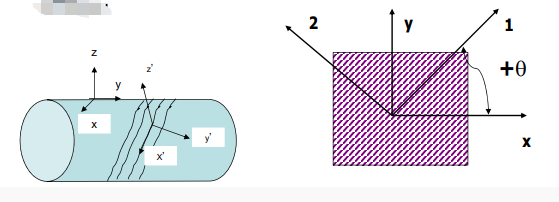
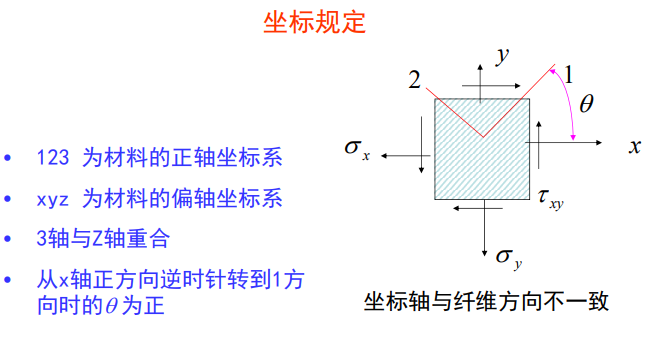
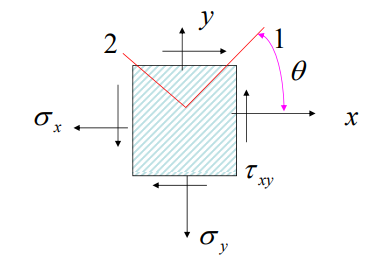
单层板的方向设定:
123坐标系为正轴坐标系一材料主轴方向;xy3坐标系为偏轴坐标系一空间坐标方向
单层板在材料主向上的应力应变关系
单层板(lamina):是指单向纤维在基体中成扁平形状的层片.
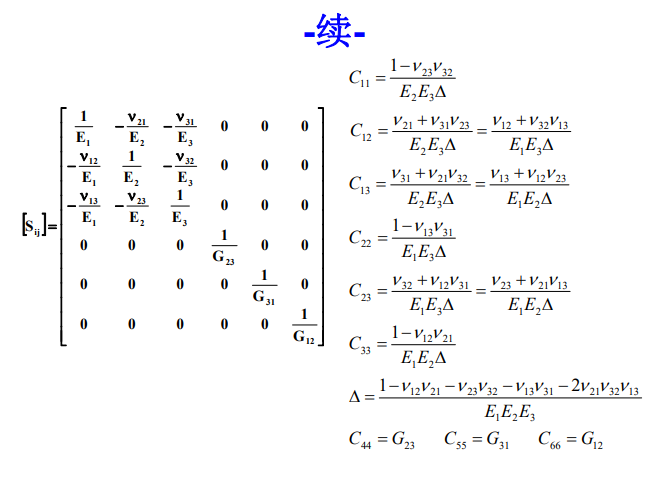
正交各向异性应力应变关系:
\[\begin{bmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\gamma_{32}\\\gamma_{13}\\\gamma_{12}\end{bmatrix}=\begin{bmatrix}S_{11}&S_{12}&S_{13}&0&0&0\\S_{21}&S_{22}&S_{23}&0&0&0\\S_{31}&S_{32}&S_{33}&0&0&0\\0&0&0&S_{44}&0&0\\0&0&0&0&S_{55}&0\\0&0&0&0&0&S_{66}\end{bmatrix}\begin{bmatrix}\sigma_1\\\sigma_2\\0\\0\\0\\\tau_{12}\end{bmatrix}
\]
考虑到 \(\sigma_3=\tau_{23}=\tau_{31}=0\) ,刚度矩阵退化为:
\[\begin{Bmatrix}\varepsilon_1\\\varepsilon_2\\\gamma_{12}\end{Bmatrix}=\begin{bmatrix}S_{11}&S_{12}&0\\S_{21}&S_{22}&0\\0&0&S_{66}\end{bmatrix}\begin{Bmatrix}\sigma_1\\\sigma_2\\\tau_{12}\end{Bmatrix}
\]
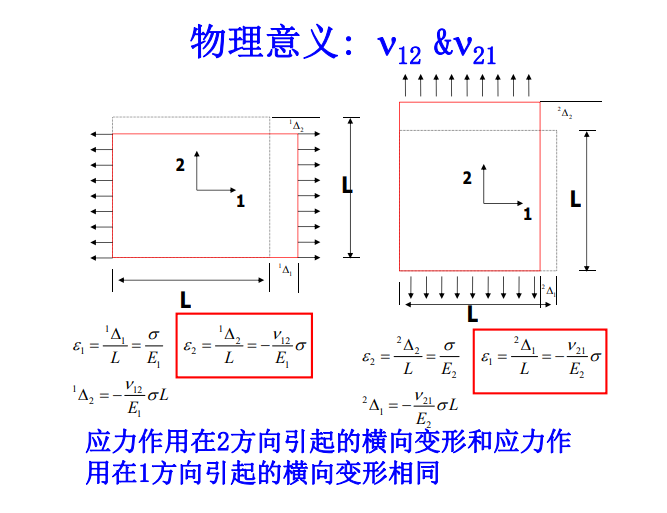
单层板法向正应变为:
\[\begin{aligned}
\mathcal{E}_{3}& =s_{13}\sigma_{1}+s_{23}\sigma_{2} \\
&=-\frac{\nu_{31}}{E_3}\sigma_1-\frac{\nu_{23}}{E_2}\sigma_2
\end{aligned}\]
用工程常数表示柔度矩阵:
\[\begin{gathered}\begin{bmatrix}S\end{bmatrix}=\begin{bmatrix}\frac{1}{E_1}&-\frac{\nu_{21}}{E_2}&0\\-\frac{\nu_{12}}{E_1}&\frac{1}{E_2}&0\\0&0&\frac{1}{G_{12}}\end{bmatrix}\\\frac{\nu_{21}}{E_2}=\frac{\nu_{12}}{E_1}\end{gathered}
\]
此时,对柔度矩阵S求逆,得到刚度矩阵\([Q]\) (这件刚度矩阵):
\[\begin{aligned} & [Q]=[S]^{-1}=\begin{bmatrix}Q_{11} & Q_{12} & 0\\ Q_{12} & Q_{22} & 0\\ 0 & 0 & Q_{66}\end{bmatrix} & \\ & Q_{11}=\frac{E_{1}}{1-\nu_{12}\nu_{21}}\quad Q_{22}=\frac{E_{2}}{1-\nu_{12}\nu_{21}} & \\ & Q_{12}=Q_{21}=\frac{\nu_{12}E_{2}}{1-\nu_{12}\nu_{21}}=\frac{\nu_{21}E_{1}}{1-\nu_{12}\nu_{21}} & \\ & Q_{66}=G_{12}\quad & \end{aligned}
\]
如果,单层板是各向同性材料,则有:
\[\begin{aligned} & \begin{Bmatrix}\varepsilon_1\\ \varepsilon_2\\ \gamma_{12}\end{Bmatrix}=\begin{bmatrix}S_{11} & S_{12} & 0\\ S_{12} & S_{11} & 0\\ 0 & 0 & 2(S_{11}-S_{12})\end{bmatrix}\begin{Bmatrix}\sigma_1\\ \sigma_2\\ \tau_{12}\end{Bmatrix}\\ & S_{11}=\frac{1}{E},S_{12}=\frac{-\nu}{E},2(S_{11}-S_{12})=\frac{1}{G}=\frac{2(1+\nu)}{E}\\ & S求逆,得Q\text{:}\quad\begin{Bmatrix}\sigma_1\\ \sigma_2\\ \tau_{12}\end{Bmatrix}=\begin{bmatrix}Q_{11} & Q_{12} & 0\\ Q_{12} & Q_{11} & 0\\ 0 & 0 & Q_{66}\end{bmatrix}\begin{Bmatrix}\varepsilon_1\\ \varepsilon_2\\ \gamma_{12}\end{Bmatrix}\\ & Q_{11}=\frac{E}{1-\nu^{2}},Q_{12}=\frac{-\nu E}{1-\nu^{2}},Q_{66}=\frac{E}{2(1+\nu)}\end{aligned}
\]
牌号
材料
Ex(GPa)
Ey(GPa)
Gxy(GPa)
Nuxy
纤维体积分数
密度(g/cm^3)
T300/5208
碳/环氧
181
10.3
7.17
.028
70%
1.6
铝
69
69
26.54
0.3
*
2.6
检验材料的试验数据或者正交各向异性材料模型的正确性:
对于各向同性材料:\(-1<\nu<1/2\)
柔度矩阵对角线上的各项应为正
\[S_{11},S_{22},S_{66}>0\quad\Rightarrow\quad E_1,E_2,G_{12}>0
\]
\[\mathcal{Q}_{ll}=E_I/(l-\nu_{l2}\nu_{2l})>0 ; E_2\nu_{12}=E_1\nu_{21}
\]
\[\Rightarrow\nu ^2{}_{l2}< E_l/ E_2 ; \nu^2_{2l}< E_2/E_l
\]
单向板在偏轴方向上的弹性特性
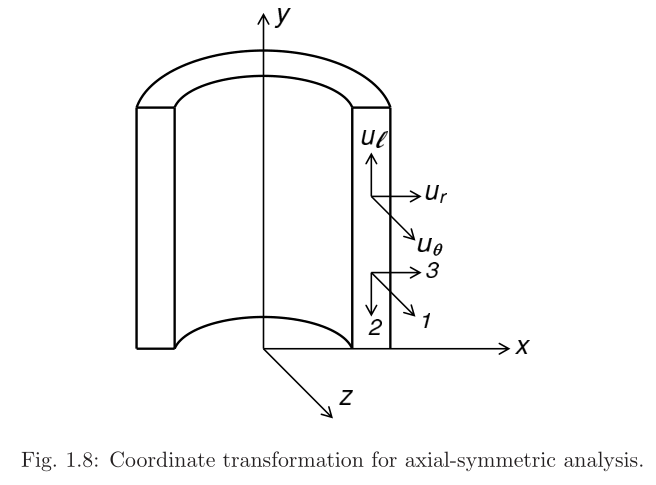
复合材料板往往由多层铺层方向不同的单层板组成.整体坐标系往往与各层材料的正轴坐标系不重合,单向板的偏轴弹性特性为单层非材料主方向的刚度.例子:对于纤维缠绕的圆柱型壳体,材料正轴是缠绕的螺旋
两套坐标系, 下面讨论应该知道应力,应变,刚度(柔度)矩阵在不同坐标系下的转化关系
三维空间中的应力-应变转换:
两个坐标系之间的关系可以用坐标轴两两之间的余弦值表示:
用x'-y'-z'坐标系中的应力来表示x-y-z坐标系中的应力的转换方程为:
\[\left\{\sigma^{\prime}\right\}=\left[A\right]\left\{\sigma\right\},\quad\left\{\sigma\right\}=\left[A\right]^{-1}\left\{\sigma^{\prime}\right\}
\]
\[\begin{bmatrix}\sigma_{x}\\ \sigma_{y}\\ \sigma_{z}\\ \tau_{yz}\\ \tau_{zx}\\ \tau_{xy}\end{bmatrix}=\begin{bmatrix}l_1^2 & m_1^2 & n_1^2 & 2m_1n_1 & 2n_1l_1 & 2l_1m_1\\ l_2^2 & m_2^2 & n_2^2 & 2m_2n_2 & 2n_2l_2 & 2l_2m_2\\ l_3^2 & m_3^2 & n_3^2 & 2m_3n_3 & 2n_3l_3 & 2l_3m_3\\ l_2l_3 & m_2m_3 & n_2n_3 & m_2n_3+m_3n_2 & n_2l_3+n_3l_2 & l_2m_3+l_3m_2\\ l_3l_1 & m_3m_1 & n_3n_1 & m_3n_1+m_1n_3 & n_3l_1+n_1l_3 & l_3m_1+l_1m_3\\ l_1l_2 & m_1m_2 & m_1n_2 & m_1n_2+m_2n_1 & n_1l_2+n_2l_1 & l_1m_2+l_2m_1\end{bmatrix}\begin{bmatrix}\sigma_{x}^{^{\prime}}\\ \sigma_{y}^{^{\prime}}\\ \sigma_{z}^{^{\prime}}\\ \sigma_{z}^{^{\prime}}\\ \tau_{yz}^{^{\prime}}\\ \tau_{zx}^{^{\prime}}\\ \tau_{xy}^{^{\prime}}\\ \end{bmatrix}
\]
同样的应变转换方程可以表示为:
\[\left\{\varepsilon^{\prime}\right\}=\left[B\right]\left\{\varepsilon\right\},\quad\left\{\varepsilon\right\}=\left[B\right]^{-1}\left\{\varepsilon^{\prime}\right\}
\]
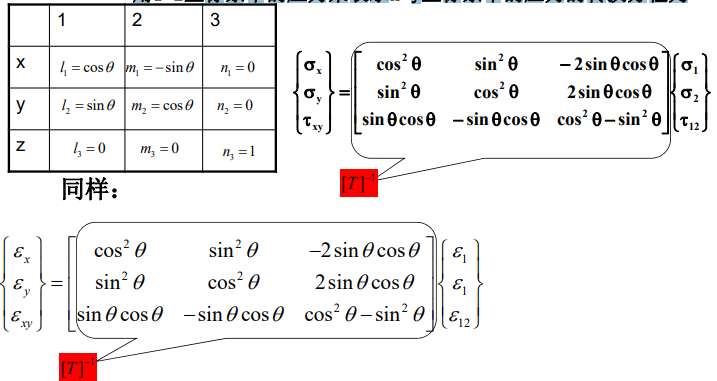
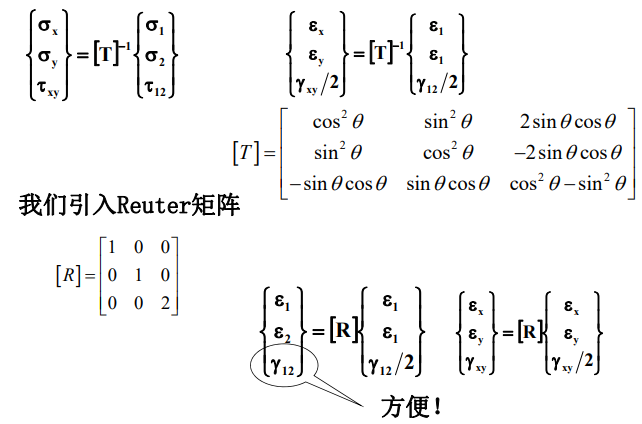
根据以上原理,用1-2坐标系中的应力来表示x-y坐标系中的应力的转换方程为:
所以,折减刚度矩阵Q在不同坐标系下的转化关系为:
\[\left([T]^{-1}\right)^T=[R][T][R]^{-1}\quad\rightarrow\quad\left[\overline{Q}\right]=[T]^{-1}[Q]\left([T]^{-1}\right)^T
\]
这就得到了单层板在x-y坐标系下的正交各向异性本构为:
六个分量,四个独立常数,广义的正交各向异性层板剪应变和正应力,剪应力和正应变存在耦合
\[\begin{Bmatrix}\sigma_\mathrm{x}\\\sigma_\mathrm{y}\\\tau_\mathrm{xy}\end{Bmatrix}=\begin{bmatrix}\overline{\mathbf{Q}}\end{bmatrix}\begin{Bmatrix}\varepsilon_\mathrm{x}\\\varepsilon_\mathrm{y}\\\gamma_\mathrm{xy}\end{Bmatrix}=\begin{bmatrix}\overline{\mathbf{Q}}_{11}&\overline{\mathbf{Q}}_{12}&\overline{\mathbf{Q}}_{16}\\\overline{\mathbf{Q}}_{12}&\overline{\mathbf{Q}}_{22}&\overline{\mathbf{Q}}_{26}\\\overline{\mathbf{Q}}_{16}&\overline{\mathbf{Q}}_{26}&\overline{\mathbf{Q}}_{66}\end{bmatrix}\begin{Bmatrix}\varepsilon_\mathrm{x}\\\varepsilon_\mathrm{y}\\\gamma_\mathrm{xy}\end{Bmatrix}
\]
其中:
\[\begin{bmatrix}T\end{bmatrix}=\begin{bmatrix}\cos^2\theta&\sin^2\theta&2\sin\theta\cos\theta\\\sin^2\theta&\cos^2\theta&-2\sin\theta\cos\theta\\-\sin\theta\cos\theta&\sin\theta\cos\theta&\cos^2\theta-\sin^2\theta\end{bmatrix}
\]
\[\begin{aligned}&\overline{Q}_{11}=Q_{11}\cos^{4}\theta+2(Q_{12}+2Q_{66})\sin^{2}\theta\cos^{2}\theta+Q_{22}\sin^{4}\theta\\&\overline{Q}_{12}=(Q_{11}+Q_{22}-4Q_{66})\sin^{2}\theta\cos^{2}\theta+Q_{12}(\cos^{4}\theta+\sin^{4}\theta)\\&\overline{Q}_{22}=Q_{11}\sin^{4}\theta+2(Q_{12}+2Q_{66})\sin^{2}\theta\cos^{2}\theta+Q_{22}\cos^{4}\theta\\&\overline{Q}_{16}=(Q_{11}-Q_{12}-2Q_{66})\sin\theta\cos^{3}\theta+(Q_{12}-Q_{22}+2Q_{66})\sin^{3}\theta\cos\theta\\&\overline{Q}_{26}=(Q_{11}-Q_{12}-2Q_{66})\sin^{3}\theta\cos\theta+(Q_{12}-Q_{22}+2Q_{66})\sin\theta\cos^{3}\theta\\&\overline{Q}_{66}=(Q_{11}+Q_{22}-2Q_{12}-2Q_{66})\sin^{2}\theta\cos^{2}\theta+Q_{66}(\cos^{4}\theta+\sin^{4}\theta)\end{aligned}
\]
可见,刚度矩阵分量是四个独立常数和角度的复杂函数;Tsai&Pagano利用三角恒等式对刚度变换进行了有创造性的改造.
\[\begin{aligned} & \mathbf{m}=\cos\theta\quad\mathbf{n}=\sin\theta\\ & \begin{Bmatrix}\overline{\mathbf{Q}}_{11}\\ \overline{\mathbf{Q}}_{22}\\ \overline{\mathbf{Q}}_{12}\\ \overline{\mathbf{Q}}_{66}\\ \overline{\mathbf{Q}}_{16}\\ \overline{\mathbf{Q}}_{26}\end{Bmatrix}=\begin{bmatrix}\mathbf{m}^4 & \mathbf{n}^4 & 2\mathbf{m}^2\mathbf{n}^2 & 4\mathbf{m}^2\mathbf{n}^2\\ \mathbf{n}^4 & \mathbf{m}^4 & 2\mathbf{m}^2\mathbf{n}^2 & 4\mathbf{m}^2\mathbf{n}^2\\ \mathbf{m}^2\mathbf{n}^2 & \mathbf{m}^2\mathbf{n}^2 & \mathbf{m}^4+\mathbf{n}^4 & -4\mathbf{m}^2\mathbf{n}^2\\ \mathbf{m}^2\mathbf{n}^2 & \mathbf{m}^2\mathbf{n}^2 & -2\mathbf{m}^2\mathbf{n}^2 & (\mathbf{m}^2-\mathbf{n}^2)^2\\ \mathbf{m}^3\mathbf{n} & -\mathbf{mn}^3 & \mathbf{mn}^3-\mathbf{m}^3\mathbf{n} & 2(\mathbf{mn}^3-\mathbf{m}^3\mathbf{n})\\ \mathbf{mn}^3 & -\mathbf{m}^3\mathbf{n} & \mathbf{m}^3\mathbf{n}-\mathbf{mn}^3 & 2(\mathbf{m}^3\mathbf{n}-\mathbf{mn}^3)\end{bmatrix}\begin{cases}\mathbf{Q}_{11}\\ \mathbf{Q}_{22}\\ \mathbf{Q}_{12}\\ \mathbf{Q}_{66}\end{cases}\end{aligned}
\]
利用三角恒等式:
\[\mathrm{m}^{4}=\cos^{4}\theta=\frac{1}{8}(3+4\cos2\theta+\cos4\theta)\\
\mathrm{m}^{3}\mathrm{n}=\cos^{3}\theta\sin\theta=\frac{1}{8}(2\sin2\theta+\sin4\theta)\\
\mathrm{m}^{2}\mathrm{n}^{2}=\cos^{2}\mathbf{\theta}\sin^{2}\mathbf{\theta}=\frac{1}{8}(1-\cos4\mathbf{\theta})\\
\mathrm{mn}^{3}=\cos\theta\sin^{3}\theta=\frac{1}{8}(2\sin2\theta-\sin4\theta)\\
\mathrm{n}^{4}=\sin^{4}\theta=\frac{1}{8}(3-4\cos2\theta+\cos4\theta)\]
进一步,可以整理为:
\[\begin{bmatrix}\bar{Q}_{11}\\\bar{Q}_{22}\\\bar{Q}_{12}\\\bar{Q}_{66}\\\bar{Q}_{16}\\\bar{Q}_{26}\end{bmatrix}=\begin{bmatrix}U_1&\cos2\theta&\cos4\theta\\U_1&-\cos2\theta&\cos4\theta\\U_4&0&-\cos4\theta\\U_5&0&-\cos4\theta\\0&\frac{1}{2}\sin2\theta&\sin4\theta\\\\0&\frac{1}{2}\sin2\theta&-\sin\theta\end{bmatrix}\begin{Bmatrix}1\\U_2\\U_3\end{Bmatrix}
\]
其中:
\[\begin{aligned}
&\mathbf{U}_{1} =(3\mathbf{Q}_{11}+3\mathbf{Q}_{22}+2\mathbf{Q}_{12}+4\mathbf{Q}_{66})/8 \\
&U_{2} =(\mathbf{Q}_{11}-\mathbf{Q}_{22})/2 \\
&U_{3} =(\mathbf{Q}_{11}+\mathbf{Q}_{22}-2\mathbf{Q}_{12}-4\mathbf{Q}_{66})/8 \\
&\mathbf{U}_{4} =(\mathbf{Q}_{11}+\mathbf{Q}_{22}+6\mathbf{Q}_{12}-4\mathbf{Q}_{66})/8 \\
&\mathbf{U}_{\mathbf{s}} =(\mathbf{Q}_{11}+\mathbf{Q}_{22}-2\mathbf{Q}_{12}+4\mathbf{Q}_{66})/8
\end{aligned}\]
分解之后:
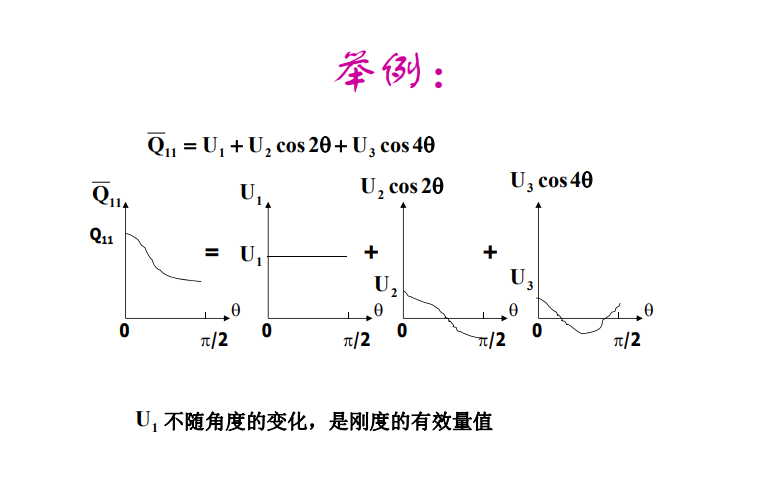
\[\overline{Q}_{11}=U_{1}+U_{2}\cos2\theta+U_{3}\cos4\theta\\
\overline{\mathbf{Q}}_{12}=\mathbf{U}_{4}-\mathbf{U}_{3}\cos4\mathbf{\theta}\\
\overline{\mathbf{Q}}_{22}=\mathbf{U}_{1}-\mathbf{U}_{2}\cos2\mathbf{\theta}+\mathbf{U}_{3}\cos4\mathbf{\theta}\\
\overline{\mathbf{Q}}_{16}=\frac{1}{2}\mathbf{U}_{2}\sin2\mathbf{\theta}+\mathbf{U}_{3}\sin4\mathbf{\theta}\\
\overline{\mathbf{Q}}_{26}=\frac{1}{2}\mathbf{U}_{2}\sin2\mathbf{\theta}-\mathbf{U}_{3}\sin4\mathbf{\theta}\\
\overline{\mathbf{Q}}_{66}=\mathbf{U}_{5}-\mathbf{U}_{3}\cos4\mathbf{\theta}\]
在绕垂直于单层板的轴旋转时,其刚度分量的部分值是不变的,U1 ,U4 ,U5为常数项,不随角度变化,有一定的含义,如拉伸模量,剪切模量等
单层板失效准则
复合材料的比应变能密度破坏准则
声明:本文仅介绍他人成果
中国科学院力学研究所在88年发的一文章,讲了一个复材准则:比应变能密度破坏准则.可以用于预测复合材料破坏强度(在什么应力状态下发生失效).
论文链接: http://www.cqvip.com/qk/94252x/19892/93249.html
这个准则假设:当单层(即lamina)中两倍比应变能密度等于1时,材料发生破坏 .数学表达式为:
\[2S_r>=1; S_r为比应变能密度
\]
比应变能\(S_r\) :
\[S_r=\frac{1}{2}(\overline \sigma_1 \overline \epsilon_1+\overline \sigma_2 \overline \epsilon_2+\overline \sigma_{12} \overline \epsilon_{12} )
\]
\(\overline \sigma_1 、\overline \epsilon_1\) 为比应力和比应变.定义如下:
\[\overline \sigma_1=\sigma_1/X; \\
\overline \sigma_2=\sigma_2/Y; \\
\overline \sigma_{12}=\sigma_{12}/S; \\
\]
\[\overline \epsilon_1=\epsilon_1/\epsilon_{1 limit};\\
\overline \epsilon_2=\epsilon_2/\epsilon_{2 limit};\\
\overline \epsilon_{12}=\epsilon_{12}/\epsilon_{12 limit};\\
\]
\[\epsilon_{1 limit}=X/E_{11};\\
\epsilon_{2 limit}=Y/E_{22};\\
\epsilon_{12 limit}=S/G_{12};\\
\]
整理得到:
\[S_r=\frac{1}{2}[(\frac{\sigma_1}{X})^2+(\frac{\sigma_2}{Y})^2-\frac{\nu_{12}}{E_{11}} \sigma_1 \sigma_2(\frac{E_{11}}{X^2}+\frac{E_{22}}{Y^2})+(\frac{\tau_{12}}{S})^2]
\]
参考资料:
材料力学性能测试方法
拉伸性能
拉伸试验是最常用的试验方法,用于测定试样在受到轴向拉伸载荷后的行为.这些试验类型可在室温或受控(加热或制冷)条件下进行,以确定材料的拉伸性能.
适用材料:
金属、塑料、弹性体、纸张、复合材料、橡胶、纺织品、粘合剂、薄膜等.
常见的拉伸试验结果:
最大载荷
最大载荷下的伸长
最大载荷做功
刚度
断裂载荷
断裂时的形变
断裂做功
弦斜率
应力应变
试验仪器:万能试验机,高速试验机等
部分测试标准:
GB/T 6397-1986<金属拉伸试验试样>
ASTM D3039-76用于测定高模量纤维增强聚合物复合材料面内拉伸性能
ASTM D638用于测定试件的拉伸强度和拉伸模量
GB/T 3354-2014 定向纤维增强聚合物基复合材料拉伸性能试验方法
压缩性能
压缩试验是一种常用于测定材料的压缩负载或抗压性的试验方法,同时也用于测定材料在受到一个特定的压缩负载并保持一段设定时间后的恢复能力.压缩试验用于测定材料在加载下的行为.此外也可测定一段时间内材料在(恒定或递增)载荷下可承受的最大应力.
压缩试验主要适用于脆性材料,如铸铁.对于塑性材料,无法测出压缩强度极限,但可以测量弹性模量、比例极限和屈服强度等.
部分测试标准
GB/T7314-2005<金属压缩实验试样>
ASTM D3410-75(剪切荷载法测定带无支撑标准截面的聚合体母体复合材料压缩特性的试验方法)
GB/T7314-2005<金属材料室温压缩试验方法>
T/CSTM 00287-2020 纤维增强聚合物基复合材料单向层合板平行纤维方向压缩性能试验方法
弯曲性能
弯曲试验是材料机械性能试验的基本方法之一,其测定材料承受弯曲载荷时的力学特性的试验.主要有三点弯曲和四点弯曲两种加载荷方式
部分测试标准:
ASTM D7624用于测定聚合物基复合材料的弯曲刚度与强度性能
GB/T232-2010<金属材料弯曲试验方法>
GB/T 41762.2-2022 纤维增强塑料复合材料 层合板厚度方向性能的测定 第2部分:弯曲试验测定碳纤维单向层合板的弹性模量、强度和威布尔尺寸效应
冲击试验
冲击试验一般是确定军用、民用设备在经受外力冲撞或作用时产品的安全性、可靠性和有效性的一种试验方法.
常用技术指标:峰值加速度、脉冲持续时间、速度变化量(半正弦波、后峰锯齿波、梯形波)和波形选择.
部分测试标准:
ISO 179-1-2010塑料摆式冲击性能的测定
GB/T 15231.5-1994 玻璃纤维增强水泥性能试验方法 抗冲击性能
GB/T 14152-2001 热塑性塑料管材耐性外冲击性能
GB/T 21239-2007 纤维增强塑料层合板冲击后压缩性能试验方
BS EN 950-1999 门扇.耐坚硬物体冲击性能的测定
DIN ISO 2747-1999 瓷釉和搪瓷.搪瓷烹调器具.耐热冲击性能的测定
GB/T 3917.1-2009 纺织品织物撕破性能
BS EN ISO 6603-1-2000塑料 硬质塑料冲孔性能的测定
T/CSTM 00286-2020 纤维增强聚合物基复合材料层合板 冲击后压缩性能试验方法
复合材料有限元分析
前置知识基础
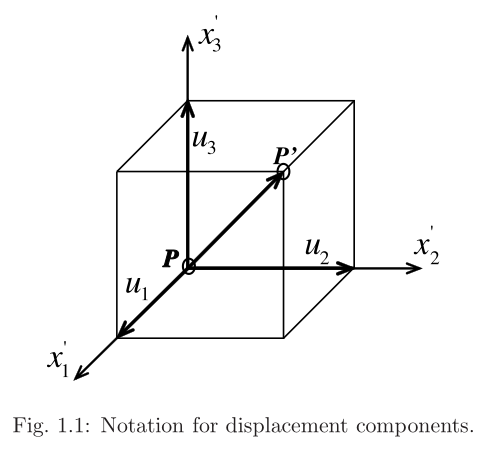
位移
单一的单层板(英文一般用lamina表示)一般认为是正交各向异性材料行为,具有三个正交的弹性对称面,三个平面的相交线构成了局部坐标系的轴,即纤维方向\((x_{1}')\) ,厚度方向\((x_{3}')\) ,还有第三根轴\((x_{2}'=x_{3}' \times x_{1}')\) .
在lamina材料坐标系下,位移表示有两种方式:\(u_i=(u_1,u_2,u_3)\) 或\(u_i=(u,v,w)\) .位移是一个向量,或者说一阶张量:
\[\mathbf u=u_i=(u_{1,}u_{2,}u_3);i=1...3
\]
拉格朗日应变张量( Lagrangian strain tensor):
\[L_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}+u_{r,i}u_{r,j})\\\text{where,} \quad u_{i,j}=\frac{\partial u_{i}}{\partial x_{j}}
\]
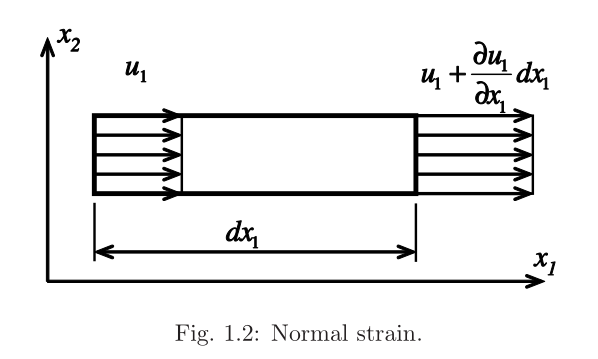
当位移梯度非常小的时候,拉格朗日应变张量可以近似为:\(\varepsilon=\varepsilon_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})\) ,应变是一个二阶对称张量.展开的定义式子:
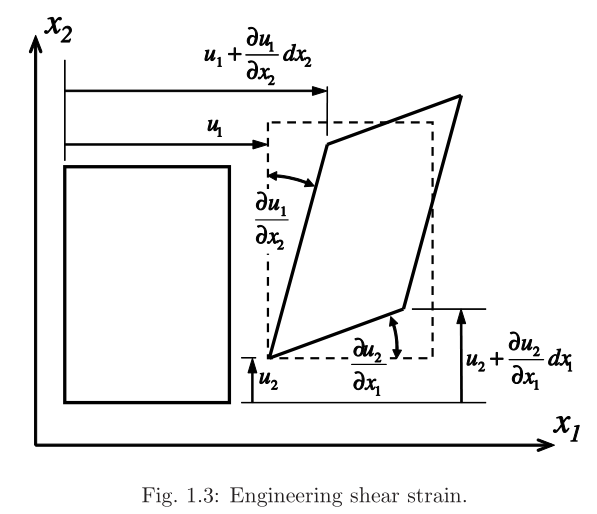
\[\begin{aligned}\varepsilon_{11}&=\frac{\partial u_1}{\partial x_1}=\epsilon_1;\quad2\varepsilon_{12}=2\varepsilon_{21}=\left(\frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1}\right)=\gamma_6=\epsilon_6\\\varepsilon_{22}&=\frac{\partial u_2}{\partial x_2}=\epsilon_2;\quad2\varepsilon_{13}=2\varepsilon_{31}=\left(\frac{\partial u_1}{\partial x_3}+\frac{\partial u_3}{\partial x_1}\right)=\gamma_5=\epsilon_5\\\varepsilon_{33}&=\frac{\partial u_3}{\partial x_3}=\epsilon_3;\quad2\varepsilon_{23}=2\varepsilon_{32}=\left(\frac{\partial u_2}{\partial x_3}+\frac{\partial u_3}{\partial x_2}\right)=\gamma_4=\epsilon_4\end{aligned}
\]
在有限元软件中,需要注意的是剪应变的选用,如ABAQUS的E12,13,23表示的是工程剪应变,而不是张量剪应变.之所以采用工程剪应变(\(\gamma = 2*\varepsilon\) ),是因为剪切模量G可以直接定义:$\tau=G\gamma $.将张量应变写成矩阵形式:
\[[\varepsilon]=\left[\begin{array}{ccc}\varepsilon_{11}&\varepsilon_{12}&\varepsilon_{13}\\\varepsilon_{12}&\varepsilon_{22}&\varepsilon_{23}\\\varepsilon_{13}&\varepsilon_{23}&\varepsilon_{33}\end{array}\right]=\left[\begin{array}{ccc}\epsilon_1&\epsilon_6/2&\epsilon_5/2\\\epsilon_6/2&\epsilon_2&\epsilon_4/2\\\epsilon_5/2&\epsilon_4/2&\epsilon_3\end{array}\right]
\]
应力张量:
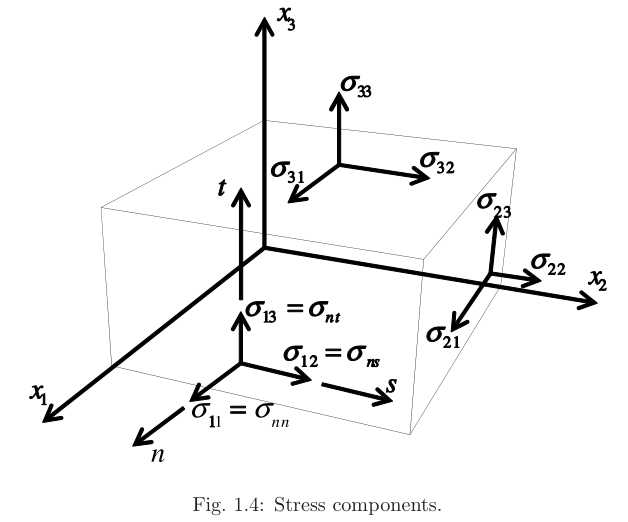
应力张量是二阶张量,能够完全描述材料一点的应力状态.一般写作:\(\sigma_{ij},with \quad i,j=1,2,3\) ,第一个下标表示所在平面的法向,第二个下标表示应力分量的方向 .应力张量的矩阵形式:
\[[\sigma]=\left[\begin{array}{ccc}\sigma_{11}&\sigma_{12}&\sigma_{13}\\\sigma_{12}&\sigma_{22}&\sigma_{23}\\\sigma_{13}&\sigma_{23}&\sigma_{33}\end{array}\right]=\left[\begin{array}{ccc}\sigma_{1}&\sigma_{6}&\sigma_{5}\\\sigma_{6}&\sigma_{2}&\sigma_{4}\\\sigma_{5}&\sigma_{4}&\sigma_{3}\end{array}\right]
\]
符号简写
因为应力,应变张量都是对称的.因此有限元中一般用Voigt矢量简化表示张量:\(\sigma_\alpha=\sigma_{ij}=\sigma_{ji}\) ,简化规则:
\[\begin{aligned}\alpha&=i&\quad if\quad i=j\\\alpha&=9-i-j&\quad if\quad i\neq j\end{aligned}
\]
根据上表,可愿意定义一个转换矩阵T,将应变应力从标准Voigt形式转换到Abaqus,Ls-dyna,Ansys等软件的应力应变形式:
\[\{\sigma_A\}=[T]\{\sigma\}
\]
\[[T]=\left[\begin{array}{cccccc}1&0&0&0&0&0\\0&1&0&0&0&0\\0&0&1&0&0&0\\0&0&0&0&0&1\\0&0&0&0&1&0\\0&0&0&1&0&0\end{array}\right]
\]
使用以上的T矩阵,就可以将应变应力从标准张量形式转换到Abaqus的notation.此外,刚度矩阵的转换为:
\[[C_A]=[T]^T[C][T]
\]
For LS-DYNAand ANSYS, the transformation matrix is:
\[[T]=\left[\begin{array}{cccccc}1&0&0&0&0&0\\0&1&0&0&0&0\\0&0&1&0&0&0\\0&0&0&0&0&1\\0&0&0&1&0&0\\0&0&0&0&1&0\end{array}\right]
\]
边界条件
Traction Boundary Conditions
力学有限元分析求解,需要指定边界条件. 边界条件可以是位移或者应力的分量指定.对于任意曲面上的一点P,牵引力\(T_{i}\) 由该点的三个分量组成.如图1.4:
\[T_{i}=\{\sigma_{nn},\sigma_{nt},\sigma_{ns}\}^T
\]
用柯西定律形式写:
\[T_i=\sigma_{ji}n_j=\sum_j^3\sigma_{ji}n_j
\]
其中\(n_j\) 是法向量,例如: 对于垂直于x1的平面,\(n_{i}=(1,0,0)\) 则:
\[T_1=\sigma_{11};\quad T_2=\sigma_{12} ;\quad T_3=\sigma_{13}
\]
Free Surface Boundary Conditions
一个曲面是自由面,等价于应力为0;\(T_n=\sigma_{nn}=0,T_t=\sigma_{nt}=0,\mathrm{and}T_s=\sigma_{ns}=0.\)
例如,当一个曲面受到纯压力加载时,对应的就是\(T_n!=0,T_t=T_s=0\) .
Continuity Conditions
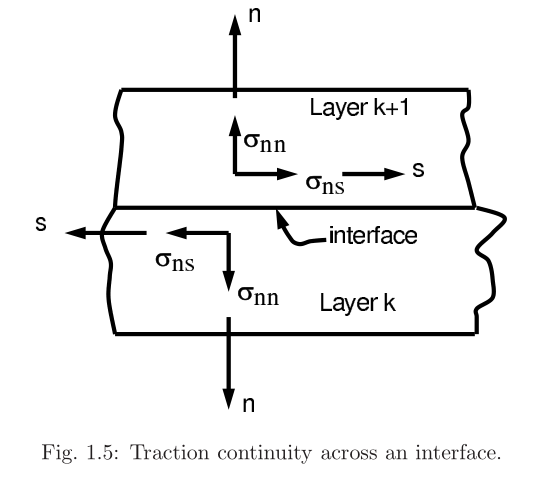
Traction Continuity(剪切连续性)
平衡要求牵引力分量\(T_i\) 必须在任何表面上连续.(在局部坐标系n(3)-t(2)-s(1)下)即:
\[\sigma_{nn}^{+}=\sigma_{nn}^{-},\sigma_{nt}^{+}=\sigma_{nt}^{-},\sigma_{ns}^{+}=\sigma_{ns}^{-}
\]
由于材料的性质在层间边界上一般是不连续的,所以应力的其他两个法向分量,一个剪切分量也是一般不满足连续性的 ,即:
\[\sigma_{tt}^{+}\neq\sigma_{tt}^{-},\sigma_{ss}^{+}\neq\sigma_{ss}^{-},\sigma_{ts}^{+}\neq\sigma_{ts}^{-}.
\]
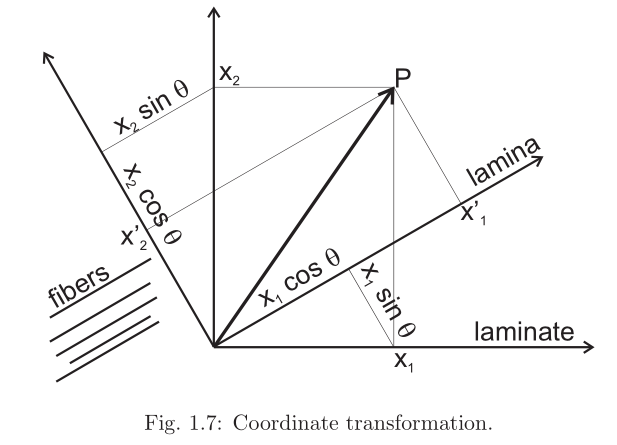
对于一点P的坐标值(x1,x2,x3)在不同坐标系下的转换.如图1.7有:
\[\begin{aligned}x_1'&=x_1\cos\theta+x_2\sin\theta\\x_2'&=-x_1\sin\theta+x_2\cos\theta\\x_3'&=x_3\end{aligned}
\]
写成矩阵形式:
\[\begin{aligned}
tensor \ notation: x_i'&=a_{ij}x_j\\
matrix \ notation:\left\{x'\right\}&=\left[a\right]\left\{x\right\}\\
\end{aligned}\]
其中,\(a_{ij}\) 是坐标变换矩阵,
所以,lamina-system到laminate-system为:\(\begin{Bmatrix}x\end{Bmatrix}=\begin{bmatrix}a\end{bmatrix}^T\begin{Bmatrix}x'\end{Bmatrix}\) ; laminate-system到lamina-system为:\(\begin{Bmatrix}x'\end{Bmatrix}=\begin{bmatrix}a\end{bmatrix}\begin{Bmatrix}x\end{Bmatrix}\)
继续使用前一节的坐标系定义,应力张量的转换关系:
\[\{\sigma'\}=[a]\{\sigma\}[a]^T
\]
此外,根据\([a]\) 可以定义6X6转换矩阵T,且有关系:
\[\sigma_\alpha'=T_{\alpha\beta}\sigma_\beta
\]
和上述同理,应变张量的转换关系,\(T_{\alpha\beta}\) 定义不变:
\[\varepsilon_\alpha'=T_{\alpha\beta}\varepsilon_\beta
\]
但考虑到一般都采用工程剪应变 \(\gamma xz,\gamma yz,\gamma xy\) ,两者的关系为(左侧为工程应变):
\[\epsilon_\delta=R_{\delta\gamma}\varepsilon_\gamma
\]
Router矩阵定义:
\[[R]=\left[\begin{array}{cccccc}1&0&0&0&0&0\\0&1&0&0&0&0\\0&0&1&0&0&0\\0&0&0&2&0&0\\0&0&0&0&2&0\\0&0&0&0&0&2\end{array}\right]
\]
因此,工程应变之间的转换关系为:
\[\begin{aligned}\epsilon_{\alpha}^{\prime}&=\overline{T}_{\alpha\beta}\epsilon_{\beta}\\\left[\overline{T}\right]&=[R][T][R]^{-1}\end{aligned}
\]
应力转换矩阵为:
注意: 应力转换矩阵和应变转换矩阵之间存在关系\([T]^{-1}=[\overline{T}]^T\)
材料坐标系下定义本构方程(使用张量应力/应变):
\[\begin{aligned}\sigma'&=\mathbf{C}':\varepsilon'\\\sigma'_{ij}&=C'_{ijkl}\varepsilon'_{kl}\end{aligned}
\]
\(C'\) 是材料坐标系下的刚度矩阵.laminate坐标系下的本构方程是: \(\{\sigma\}=[C]\{\epsilon\}\) ,刚度矩阵的转换关系如下:
\[[C]=[\overline{T}]^T[C^{\prime}][\overline{T}]
\]
\[[C^{\prime}]=[\overline{T}]^{-T}[C][\overline{T}]^{-1}=[T][C][T]^T
\]
3d 本构方程
已经在几种各向异性弹性力学的本构方程 这节说过了,就不赘述.
3D本构退化到2D平面应力方程
弹性力学中2D公式有:平面应力和平面应变. 平面应变假设:
\[\begin{array}{lcl}u&=&u\left(x,y\right)\\v&=&v\left(x,y\right)\\w&=&0\end{array}
\]
换成应变就是:
\[\begin{array}{lllllll}u&=&u\left(x,y\right)&&&&\\v&=&v\left(x,y\right)&&&&\\\varepsilon_{zz}&=&\varepsilon_{xz}&=&\varepsilon_{yz}&=&0\end{array}
\]
平面应力状态假设:与 z 方向有关的三个应力张量分量为零.但是只有在厚度趋近于零的极限时才完全正确
\[u=u(x,y),v=v(x,y),\sigma_{z}=\sigma_{xz}=\sigma_{yz}=0
\]
所以在平面应力状态下,本构方程为:
\[\left\{\begin{array}{c}\epsilon_1'\\\epsilon_2'\\\epsilon_3'\\\gamma_4'\\\gamma_5'\\\gamma_6'\end{array}\right\}=\left[\begin{array}{cccccc}S_{11}'&S_{12}'&S_{13}'&0&0&0\\S_{12}'&S_{22}'&S_{23}'&0&0&0\\S_{13}'&S_{23}'&S_{33}'&0&0&0\\0&0&0&S_{44}'&0&0\\0&0&0&0&S_{55}'&0\\0&0&0&0&0&S_{66}'\end{array}\right]\left\{\begin{array}{c}\sigma_1'\\\sigma_2'\\\sigma_3'=0\\\sigma_4'\\\sigma_5'\\\sigma_6'\end{array}\right\}
\]
从而可以得到3X3的面内缩减柔度矩阵 公式:
\[\left\{\begin{array}{c}\epsilon_1'\\\epsilon_2'\\\gamma_6'\end{array}\right\}=\left[\begin{array}{ccc}S_{11}'&S_{12}'&0\\S_{12}'&S_{22}'&0\\0&0&S_{66}'\end{array}\right]\left\{\begin{array}{c}\sigma_1'\\\sigma_2'\\\sigma_6'\end{array}\right\}
\]
求逆操作后得到面内折减刚度矩阵 \([Q^{\prime}]=[S_{3\times3}^{\prime}]^{-1}\) :
\[\left\{\begin{array}{c}\sigma_1'\\\sigma_2'\\\sigma_6'\end{array}\right\}=\left[\begin{array}{ccc}Q_{11}'&Q_{12}'&0\\Q_{12}'&Q_{22}'&0\\0&0&Q_{66}'\end{array}\right]\left\{\begin{array}{c}\epsilon_1'\\\epsilon_2'\\\gamma_6'\end{array}\right\}
\]
需要注意的是面内缩减柔度矩阵\(\begin{bmatrix}S'_{3\times3}\end{bmatrix}\) 和6X6的柔度矩阵在数值上是对应的;但是 面内折减刚度矩阵 \([Q^{\prime}]\) 和6X6的刚度矩阵是不对应的.这是因为面内折减刚度矩阵\(Q'\) 由3X3柔度阵求逆得到,C'是由6X6柔度阵求逆得到.
而面外相关的公式为:
\[\epsilon_3'=S_{13}'\sigma_1'+S_{23}'\sigma_2'
\]
\[\left\{\begin{array}{c}\gamma_4'\\\gamma_5'\end{array}\right\}=\left[\begin{array}{cc}S_4'&0\\0&S_{55}'\end{array}\right]\left\{\begin{array}{c}\sigma_4'\\\sigma_5'\end{array}\right\}
\]
\[\left\{\begin{array}{c}\sigma_4'\\\sigma_5'\end{array}\right\}=\left[\begin{array}{cc}C_{44}'&0\\0&C_{55}'\end{array}\right]\left\{\begin{array}{c}\gamma_4'\\\gamma_5'\end{array}\right\}
\]
均衡对称层合板的等效模量计算
均衡对称层合板的刚度矩阵为:
\[\begin{aligned}[C]=\sum_{k=1}^N\frac{t_k}{t}[C_k]\end{aligned}
\]
柔度矩阵不能简单相加,也不能求平均值.所以层合板的柔度矩阵\([S]=[C]^{-1}\) .这种层合板具有正交各向异性的刚度/柔度矩阵:
\[\left.\left[S\right]=\left[\begin{array}{ccccccc}\frac{1}{E_x}&-\frac{\nu_{yx}}{E_y}&-\frac{\nu_{zx}}{E_z}&0&0&0\\-\frac{\nu_{xy}}{E_x}&\frac{1}{E_y}&-\frac{\nu_{zy}}{E_z}&0&0&0\\-\frac{\nu_{xz}}{E_x}&-\frac{\nu_{yz}}{E_y}&\frac{1}{E_z}&0&0&0\\0&0&0&\frac{1}{G_{yz}}&0&0\\0&0&0&0&\frac{1}{G_{xz}}&0\\0&0&0&0&0&\frac{1}{G_{xy}}\end{array}\right.\right]
\]
等效模量如下求得:
\[\begin{aligned}
E_{x}& =1/S_{11} \quad \nu_{xy} =-S_{21}/S_{11} \\
E_{y}& =1/S_{22} \quad \nu_{xz} =-S_{31}/S_{11} \\
E_{z}& =1/S_{33} \quad \nu_{yz} =-S_{32}/S_{22} \\
G_{yz}& =1/S_{44} \\
G_{xz}& =1/S_{55} \\
G_{xy}& =1/S_{66} \\
\end{aligned}\]





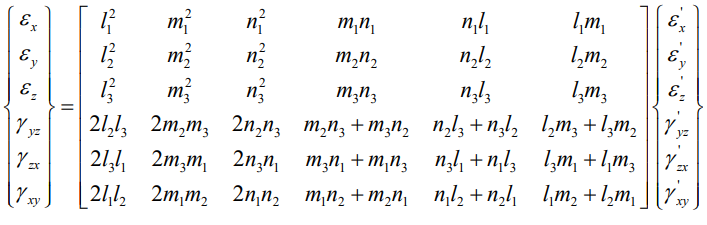




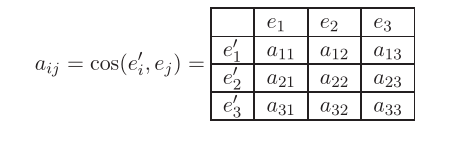






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南